1 Introduction

1-Hexene (IUPAC name), also known as hex-1-ene, hexylene, or butyl ethylene, has the molecular formula of C6H12. It is an industrially significant linear alpha olefin, with primary use as a co-monomer in the production of high-density and linear low-density polyethylene. It is also employed in the production of linear aldehydes, isoprene, and higher fatty alcohols. Furthermore, 1-hexene is employed as a hydrophobe in oil-soluble surfactants, as a lubricating fluid, and as a catalyzer [1].

There is currently no reference correlation for the viscosity, nor the thermal conductivity of 1-hexene, probably attributed to the fact that an equation of state for 1-hexene has only just now been published [2].

In a series of papers published over the last ten years, we reported new reference correlations over extended temperature and pressure ranges, for the viscosity of some simple fluids (xenon [3], water,[4], deuterium oxide [5], ammonia [6]), hydrocarbons (n-hexane [7], n-heptane,[8], n-undecane [9], n-hexadecane [10], benzene [11], toluene [12], cyclopentane [13]), alcohols (methanol [14], ethanol [15], ethane-1,2-diol [16], propane-1,2-diol [17]) and some refrigerants (R-1234yf and R-1234ze(E) [18], R-134a [19], R-161 [20], R-245fa [21], and R-32 [22]).

In the case of the thermal conductivity, we also reported new reference correlations over extended temperature and pressure ranges, for some simple fluids (xenon [23], n- and p-hydrogen [24], water [25], deuterium oxide [26], carbon dioxide [27], ammonia [28], sulfur hexafluoride [29]), hydrocarbons (n-pentane, iso-pentane and cyclopentane [30], n-hexane [31], n-heptane [32], n-undecane [9], n-hexadecane [10], ethene and propene [33], benzene [34], toluene [35], o-, m-, and p-xylene, and ethylbenzene [36], cyclohexane [37]), alcohols (ethanol [38], ethane-1,2-diol [39]), and some refrigerants (R-1233zd(E) [40], R-161 [20], R-245fa [21], and RE-347mcc [41]).

In this paper, the methodology adopted in the aforementioned papers is extended to develo** new reference correlations for the viscosity and thermal conductivity of 1-hexene. Thus, the goal of this work is to critically assess the available literature data, and provide wide-ranging correlations for the viscosity and thermal conductivity of 1-hexene that are valid over gas, liquid, and supercritical states, and incorporate densities provided by the recently published equation of state of Betken et al. [2].

The analysis we use is based on the best available experimental data. A prerequisite to the analysis is a critical assessment of the experimental data. Here we define two categories of experimental data: primary data, employed in the development of the correlation, and secondary data, used simply for comparison purposes. According to the recommendation adopted by the Subcommittee on Transport Properties (now known as The International Association for Transport Properties) of the International Union of Pure and Applied Chemistry, the primary data are identified by a well-established set of criteria [42] These criteria have been successfully employed to establish standard reference values for the viscosity and thermal conductivity of fluids over wide ranges of conditions, with uncertainties in the range of 1 %. However, in many cases, such a narrow definition unacceptably limits the range of the data representation. Consequently, within the primary data set, it is also necessary to include results that extend over a wide range of conditions, albeit with a poorer accuracy, provided they are consistent with other more accurate data or with theory. In all cases, the accuracy claimed for the final recommended data must reflect the estimated uncertainty in the primary information.

The development of the correlation requires densities; Betken et al. [2] has recently published an accurate, wide-ranging Helmholtz-energy equation of state valid from the triple point up to 535 K and 245 MPa, with an uncertainty of 0.18 % (95 % confidence level) in density. We use the Betken et al. [2] for all thermodynamic properties and also adopt their values for the critical point and triple point. The critical temperature, Tc, and the critical density, ρc, are 504.00 K and 238.1713 kg·m−3, respectively [2] and the triple-point temperature is 133.39 K [2].

2 The Viscosity Correlation

The viscosity η can be expressed [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] as the sum of four independent contributions, as

$$\eta \,(\rho ,T) ={\eta_0}(T)\;\, + \;\,{\eta_1}{\kern 1pt} (T)\rho \,\; + \;\,{\Delta }\eta (\rho ,T)\,\; + \;\,{\Delta }{\eta_{\text{c}}}(\rho ,T),$$
(1)

where ρ is the molar density, T is the absolute temperature, and the first term, η0(Τ) = η(0,Τ), is the contribution to the viscosity in the dilute-gas limit, where only two-body molecular interactions occur. The linear-in-density term, η1(Τ) ρ, known as the initial density dependence term, can be separately established with the development of the Rainwater-Friend theory [43,44,45] for the transport properties of moderately dense gases. The critical enhancement term, Δηc(ρ,Τ), arises from the long-range density fluctuations that occur in a fluid near its critical point, which contribute to divergence of the viscosity at the critical point. This term for viscosity is significant only in the region very near the critical point, as shown in Vesovic et al. [46] and Hendl et al. [47]. For CO2, Vesovic et al. [46] showed that the enhancement contributes greater than 1 % to the viscosity only in the small region bounded by 0.986 < Tr < 1.019 and 0.642 < ρr < 1.283 (where Tr and ρr denote the reduced temperature and density). Since data close to the critical point are unavailable, Δηc(ρ,Τ) will be set to zero in Eq. 1 and not discussed further. Finally, the term Δη(ρ,T), the residual term, represents the contribution of all other effects to the viscosity of the fluid at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer.

The identification of these four separate contributions to the viscosity and to transport properties in general is useful because it is possible in general, to some extent, to treat η0(Τ), and η1(Τ) theoretically. In addition, it is possible to derive information about both η0(Τ) and η1(Τ) from experiment. In contrast, there is little theoretical guidance concerning the residual contribution, Δη(ρ,Τ), and therefore its evaluation is based entirely on an empirical equation obtained by fitting experimental data.

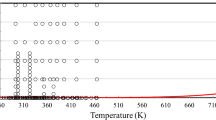
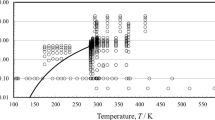
Table 1 summarizes, to the best of our knowledge, the experimental measurements of the viscosity of 1-hexene reported in the literature. Probably the most accurate measurements are those performed by Sagdeev et al. [1] in a falling-body viscometer over a temperature range 298 to 472 K and up to a pressure of 245 MPa, with an uncertainty of 1.5–2.0 % (at the 95 % confidence level). The measurements of Naziev et al. [54] were not included in the primary data set, as they have been retaken by Guseinov et al. [50], as they stated that the “Capillary viscometer is not suited for measuring the viscosity of olefinic hydrocarbons due to their aggressiveness with respect to mercury (when higher olefins come into contact with mercury, mercury-liquid emulsion closes the passage of the capillary)”. Furthermore the 293.15 K isotherm of Guseinov and Galandarov [49] (7 points), as well as the 298.15 K isotherm of Guseinov et al. [50] (7 points), were not included in develo** the correlation, as they showed an inexplicable 10 % deviation from all other measurements—also pointed out by Sagdeev et al. [1]. No other data, to our knowledge, are available for the viscosity of 1-hexene.

Table 1 Viscosity measurements of 1-hexene
Full size table

Figures 1 and 2 show the ranges of the primary measurements outlined in Table 1, and the phase may be seen as well.

Fig. 1
figure 1

Temperature–pressure ranges of the primary experimental viscosity data for 1-hexene, (––) saturation curve

Full size image
Fig. 2
figure 2

Temperature-density ranges of the primary experimental viscosity data for 1-hexene, (––) saturation curve

Full size image

2.1 The Viscosity Dilute-Gas Limit

The dilute-gas limit viscosity, η0(Τ) is a function only of temperature and can be analyzed independently of all other contributions in Eq. 1. According to the kinetic theory, the viscosity of a pure polyatomic gas may be related to an effective collision cross section, which contains all the dynamic and statistical information about the binary collision. For practical purposes, this relation is formally identical to that of monatomic gases and can be written as [55]

$$\eta_{0}(T) = 0.02669\frac{\sqrt{MT}}{{\sigma^2}{\varOmega^{(2,2)}}}$$
(2)

where M (84.15948 g·mol−1) is the molar mass, the collision diameter σ in nm is the smallest separation distance where the intermolecular potential function is equal to zero, T is the temperature in K, and the resulting viscosity is in μPa s. Ω(2,2) is a collision integral that depends upon the potential function.

In the case of nonpolar gases, Neufeld et al. [56] developed an empirical correlation for the Ω(2,2) collision integral for the Lennard–Jones (12–6) potential, as a function of the dimensionless temperature T* = T/(ε/kB) (where kB is Boltzmann’s constant and ε is the Lennard–Jones energy parameter), as

$$\begin{aligned} {\Omega^{(2,2)}}({T^*}) & = 1.16145{({T^*})^{ - 0.14874}} + 0.52487\,{{\text{e}}^{ - 0.7732{T^*}}} + 2.16178\,{{\text{e}}^{ - 2.43787{T^*}}} \\ & \quad - 6.435 \times {10^{ - 4}}{({T^*})^{0.14874}}\sin [18.0323{({T^*})^{ - 0.7683}} - 7.27371]. \hfill \\ \end{aligned}$$
(3)

Equations 2 and 3 form a consistent scheme for the calculation of the dilute-gas limit viscosity as a function of the temperature, the only unknowns being the parameters σ and ε. The gas-phase low-pressure measurements of Lyuesternik and Zhdanov [51] and McCoubrey et al. [53] were employed for this calculation. The values for σ and ε obtained are shown in Table 2.

Table 2 Coefficients and parameters for Eqs. 2 to 8
Full size table

Figure 3 shows the gas-phase low-pressure data and the calculated results for η0 using Eqs. 2 and 3. The values recommended by Lyuesternik and Zhdanov [51] are also shown. These were obtained by an oversimplification of the kinetic theory with parameters generalized for a very large number of gases [51]. As the range of experimental data is limited, having theoretical guidance provides physically reasonable behavior upon extrapolation outside of the range of data.

Fig. 3
figure 3

Dilute-gas viscosity, η0, as a function of the temperature: Lyuesternik and Zhdanov [51] (◯), McCoubrey et al. [53] (△), recommended values of Lyuesternik and Zhdanov [51] (–-)

Full size image

For ease of use in calculations, η0 values calculated from Eqs. 2 and 3 over the temperature range 140 to 1500 K were fitted using a commercial program ([57]) to a rational polynomial:

$${\eta_0}({T_{\text{r}}}) = \frac{{\sum\limits_{i = 0}^5 {{b_i}T_{\text{r}}^i} }}{{\sum\limits_{i = 0}^2 {{c_i}T_{\text{r}}^i} }},$$
(4)

where the units for η0 are μPa s, the reduced temperature is Tr = (T/Tc), and the coefficients bi and ci are in Table 2. Equation 4 reproduces the values calculated by Eqs. 2 and 3 to within 0.05 % up to 1500 K, and thus it will be employed hereafter. If there is a need to explore behavior above 1500 K, Eqs. 2 and 3 should be used and one should consider the thermal decomposition [58]. Figure 4 shows the deviations of the measurements from the scheme of Eqs. 2 and 3. The agreement in the range of existing data is within 1.2 %.

Fig. 4
figure 4

Dilute-gas viscosity deviations from the values obtained by the scheme of Eqs. 2 and 3, as a function of the temperature: Lyuesternik and Zhdanov [51] (◯), McCoubrey et al. [53] (△), recommended values of Lyuesternik and Zhdanov [51] (–-), and values calculated from Eq. 4 (▬)

Full size image

2.2 The Initial-Density Dependence Viscosity Term

The temperature dependence of the linear-in-density coefficient of the viscosity η1(T) in Eq. 1 is very large at subcritical temperatures and must be taken into account to obtain an accurate representation of the behavior of the viscosity in the vapor phase. It changes sign from positive to negative as the temperature decreases. Therefore, the viscosity along an isotherm should first decrease in the vapor phase and subsequently increase with increasing density [55]. Vogel et al. [59] have shown that fluids exhibit the same general behavior of the initial density dependence of viscosity, which can also be expressed by means of the second viscosity virial coefficient Bη(T) in m3·kg−1, as

$$B_{\upeta}(T) = \frac{{{\eta_1}(T)}}{{{\eta_0}(T)}}.$$
(5)

The second viscosity virial coefficient can be obtained according to the theory of Rainwater and Friend [43, 44] as a function of a reduced second viscosity virial coefficient, Bη*(T*), as

$$B_{\upeta}^{\ast}({T^{\ast}}) = \frac{{{B_{\upeta }}(T)}}{{{N_{\text{A}}}\,{\sigma^3}}},$$
(6)

where [55]

$$B_{\upeta }^*({T^*}) = \sum\limits_{\iota = 0}^6 {{d_i}{{({T^*})}^{ - 0.25i}}} + {d_7}{({T^*})^{ - 2.5}} + {d_8}{({T^*})^{ - 5.5}}.$$
(7)

In the above equations, NA is the Avogadro constant. The coefficients di from Ref. [55] are given in Table 2.

2.3 The Viscosity Residual Term

The residual viscosity term Δη(ρ,T), represents the contribution of all other effects to the viscosity of the fluid at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer. Because there is little theoretical guidance concerning this term, its evaluation here is based entirely on experimentally obtained data.

The procedure adopted during this analysis used symbolic regression software [60] to fit all the primary data to the residual viscosity. Symbolic regression is a type of genetic programming that allows the exploration of arbitrary functional forms to regress data. The functional form is obtained by use of a set of operators, parameters, and variables as building blocks. In the present work we restricted the operators to the set (+ , − , *, /) and the operands (constant, Tr, ρr), with Tr = T/Tc and ρr = ρ/ρc. In addition, we adopted a form suggested from the hard-sphere model employed by Assael et al. [61] Δη(ρr,Tr) = (ρr2/3Tr1/2)F(ρr,Tr), where the symbolic regression method was used to determine the functional form for F(ρr,Tr). For this task, the dilute-gas limit and the initial density dependence terms were calculated for each experimental point (employing Eqs. 4 to 7) and subtracted from the experimental viscosity to obtain the residual term. The final equation obtained was

$${\Delta }\eta (\rho ,{\rm T}) = \left( {\rho_{\text{r}}^{2/3}T_{\text{r}}^{1/2}} \right)\left\{ {{f_0}{\rho_{\text{r}}}\left( {1 + \frac{1}{{{T_{\text{r}}}}}} \right) + \frac{{{f_1}{\rho_{\text{r}}} + {f_2}\rho_{\text{r}}^5}}{{{f_3} + {f_4}T_{\text{r}} + {f_5}{\rho_{\text{r}}} + \rho_{\text{r}}^2 + {f_6}T_{\text{r}}\rho_{\text{r}}}}} \right\}.$$
(8)

The coefficients are given in Table 2.

2.4 Comparison with Data

The final correlation model consists of Eq. 1, and Eqs. 4 to 8 with the critical enhancement term set to zero. Table 3 summarizes comparisons of the primary data with the correlation. We define the percent deviation as PCTDEV = 100(ηexp − ηfit)/ηfit, where ηexp is the experimental value of the viscosity and ηfit is the value calculated from the correlation. The average absolute percent deviation (AAD) is found with the expression AAD = (∑│PCTDEV│)/n, where the summation is over all n points, the bias percent is found with the expression BIAS = (∑PCTDEV)/n.

Table 3 Evaluation of the 1-hexene viscosity correlation for the primary data
Full size table

The average absolute percentage deviation of the fit for the primary data is 1.94 %, with a bias of − 0.55 %, while the estimated uncertainty of the correlation in the temperature range 160 to 580 K and up to 245 MPa is 4.8 % (at the 95 % confidence level). Due to the omission of a critical enhancement term, in the near vicinity of the critical point the uncertainty can be larger.

Figure 5 shows the relative deviations of the primary viscosity data of 1-hexene from the values calculated by Eqs. 1, 4 to 8, as a function of temperature, while Figs. 6 and 7 show the same deviations but as a function of the pressure and the density.

Fig. 5
figure 5

Relative deviations of the viscosity of the primary experimental data of 1-hexene from the values calculated by the present model, Eqs. 1, 4 to 8, as a function of temperature. Sagdeev et al. [1] (△), Torín-Ollarves et al. [48] (▲), Guseinov and Galandarov [49] (◊), Guseinov et al. [50] (◆), Lyuesternik and Zhdanov [51] (), Wright [52] (●), and McCoubrey et al. [53] (◯)

Full size image
Fig. 6
figure 6

Relative deviations of the viscosity of primary experimental data of 1-hexene from the values calculated by the present model, Eqs. 1, 4 to 8, as a function of pressure. Sagdeev et al. [1] (△), Torín-Ollarves et al. [48] (▲), Guseinov and Galandarov [49] (◊), Guseinov et al. [50] (◆), Lyuesternik and Zhdanov [51] (), Wright [52] (●), and McCoubrey et al. [53] (◯)

Full size image
Fig. 7
figure 7

Relative deviations of the viscosity of primary experimental data of 1-hexene from the values calculated by the present model, Eqs. 1, 4 to 8, as a function of density. Sagdeev et al. [1] (△), Torín-Ollarves et al. [48] (▲), Guseinov and Galandarov [49] (◊), Guseinov et al. [50] (◆), Lyuesternik and Zhdanov [51] (), Wright [52] (●), and McCoubrey et al. [53] (◯)

Full size image

The average absolute percent deviation (AAD) and the bias for the secondary data of Naziev were 3.67 and − 2.24, respectively.

Finally, Fig. 8 shows a plot of the viscosity of 1-hexene as a function of the temperature for different pressures. The plot demonstrates the physically reasonable extrapolation behavior at pressures higher than 245 MPa, and at temperatures that exceed the 580 K limit of the current measurements and the 535 K limit of the EOS. However, the reader should be aware that thermal decomposition may occur at higher temperatures [58], and this is not accounted for in our correlation.

Fig. 8
figure 8

Viscosity of 1-hexene as a function of the temperature for different pressures

Full size image

3 The Thermal Conductivity Correlation

In a very similar fashion to that described for the expression of viscosity in Sect. 2, the thermal conductivity λ is expressed as the sum of three independent contributions, as

$$\lambda (\rho ,T) = {\lambda_{\text{o}}}(T) + {\Delta }\lambda (\rho ,T) + {\Delta }{\lambda_{\text{c}}}(\rho ,T)$$
(9)

where ρ is the density, T is the temperature, and the first term, λο(Τ) = λ(0,Τ), is the contribution to the thermal conductivity in the dilute-gas limit, where only two-body molecular interactions occur. The final term, Δλc(ρ,Τ), the critical enhancement, arises from the long-range density fluctuations that occur in a fluid near its critical point, which contribute to divergence of the thermal conductivity at the critical point. Finally, the term Δλ(ρ,T), the residual property, represents the contribution of all other effects to the thermal conductivity of the fluid at elevated densities.

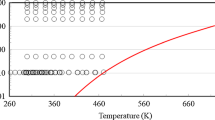
Table 4 summarizes, to the best of our knowledge, the experimental measurements of the thermal conductivity of 1-hexene reported in the literature. As all investigators reported uncertainties of less than 2 %, they were all included in the primary data set, with the exception of the measurements of Tarzimanov et al. [71], that were 10 % lower than all the rest—also pointed out by the authors themselves. Furthermore, it should be pointed out that the ten thermal-conductivity measurements at 623 K of Naziev and Abasov [67] showed unexpectedly higher deviations than all the rest, and thus they were not included in the correlation.

Table 4 Thermal conductivity measurements of 1-hexene
Full size table

Figures 9 and 10 show the ranges of the primary measurements outlined in Table 4, and the phase may be seen as well. The development of the correlation requires densities. As already discussed in the case of the viscosity correlation, we employed the Helmholtz-energy equation of state of Betken et al. [2].

Fig. 9
figure 9

Temperature–pressure ranges of the primary experimental thermal conductivity data for 1-hexene, (––) saturation curve

Full size image
Fig. 10
figure 10

Temperature-density ranges of the primary experimental thermal conductivity data for 1-hexene, (––) saturation curve

Full size image

3.1 The Thermal Conductivity Dilute-Gas Limit

In order to extrapolate the temperature range of the measurements, a theoretically-based scheme was preferred to correlate the dilute-gas limit thermal conductivity, λο(Τ), over a wide temperature range. The traditional kinetic approach for thermal conductivity results in an expression involving three generalized cross sections [72, 73]. However, it is possible to derive an equivalent kinetic theory expression for thermal conductivity by making use of the approach of Thijsse et al. [74] and Millat et al. [75], where one considers expansion in terms of total energy, rather than separating translational from internal energy as is done traditionally. In this case, the dilute-gas limit thermal conductivity, λο(Τ) (mW·m−1·K−1), of a polyatomic gas can be shown to be inversely proportional to a single generalized cross section [72,73,74,75], S(10E) (nm2), as

$${\lambda_{\text{o}}}(T)\;\; = \;\;1000\frac{{5k_{\text{B}}^2(1 + {r^2})\;T}}{{2m\;{{\langle \nu \rangle }_{\text{o}}}\;S(10E)}}{f_\lambda },$$
(10)

where kB is the Boltzmann constant (1.380649 × 10–23 J·K–1 [76]), T (K) is the absolute temperature, fλ (–) is the dimensionless higher-order correction factor, m (kg) is the molecular mass of 1-hexene [(0.08415948/6.02214076 × 1023) kg], and \(\langle \nu \rangle_{\text{o}}=4\sqrt{k_{\text{B}}T/\pi m}\) (m/s) is the average relative thermal speed. The quantity r2 is defined by r2 = 2Cinto/5kB, where Cinto is the contribution of both the rotational, Croto, and the vibrational, Cvibo, degrees of freedom to the isochoric ideal-gas heat capacity Cvo.

The recent classical trajectory calculations [77,78,79] confirm that for most molecules studied, the higher-order thermal-conductivity correction factor is near unity. One can take advantage of this finding to define the effective generalized cross section Sλ (= S(10E)/fλ) (nm2), and rewrite Eq. 10 for the dilute-gas limit thermal conductivity of 1-hexene, λο(Τ) (mW·m−1·K−1), as

$${\lambda_0}(T) = 0.06080851\frac{{(C_p^{\text{o}}/{k_{\text{B}}})\sqrt T }}{{S_\lambda }}.$$
(11)

The ideal-gas isobaric heat capacity, \(C_{p}^{\text{o}}(={C_{{\text{int}}}^{\text{o}}}+2.5k_{\rm B})\) in (J/K), can be obtained from Betken et al. [2] as

$$\frac{{C_p^{\text{o}}}}{{{k_{\text{B}}}}}\; = \;4 + \sum\limits_{k = 1}^3 {{v_k}{{\left( {\frac{{u_k}}{T}} \right)}^2}\frac{{\exp ({u_k}/T)}}{{{{\left[ {\exp ({u_k}/T) - 1} \right]}^2}}}},$$
(12)

where the values of the coefficients νk and uk are: ν1 = 8.65, ν2 = 14.10, ν3 = 21.90, and u1 = 360 Κ, u2 = 3534 K, u3 = 1473 Κ.

It has been previously noted [75], and confirmed [73] for smaller molecules, that the cross section S(10E) exhibits an almost linear dependence on the inverse temperature. Hence, in order to develop the correlation, we have fitted the effective cross section Sλ (nm2), obtained from the low-density data of Nesterov et al. [64], Vargaftik and Vanicheva [65], Naziev and Abasov [67], and Naziev and Abasov [70], shown in Table 4, by means of Eq. 13, to a linear fit in inverse temperature, resulting in the following expression,

$${S_\lambda } = 0.3746 \, + \, \frac{{{280}{\text{.2921}}}}{\rm T}.$$
(13)

Equations 11 to 13 form a consistent set of equations for the calculation of the dilute-gas limit thermal conductivity of 1-hexene.

The values of the dilute–gas limit thermal conductivity, λ0(Τ) in mW·m−1·K−1, obtained by the scheme of Eqs. 11 to 13, were fitted as a function of the reduced temperature Tr = T / Tc for ease of use to the following equation:

$${\lambda_0}(T) = \frac{{ - 0.402537 + 3.55864{T_{\text{r}}} - 0.398674T_{\text{r}}^2 - 17.2629T_{\text{r}}^3 + 52.3353T_{\text{r}}^4 - 13.8719T_{\text{r}}^5 + 1.30184T_{\text{r}}^{6}}}{{0.238788 - 0.526011{T_{\text{r}}} + T_{\text{r}}^2}}.$$
(14)

Values calculated by Eq. 14 do not deviate from the values calculated by the scheme of Eqs. 11 to 13 by more than 0.4 % over the temperature range from the triple point to 1500 K. Equation 14 is hence employed in the calculations that will follow.

Figure 11 shows the dilute-gas thermal conductivity as a function of temperature, while Fig. 12 shows their deviations from the values obtained by the scheme of Eqs. 11 to 13. The selected data are represented within the uncertainty of the data. No obvious systematic trends are observed. Therefore, based on the aforementioned discussion, Eqs. 11 to 13 or Eq. 14 represent the dilute-gas limit thermal conductivity to within 3 % at the 95 % confidence level.

Fig. 11
figure 11

Dilute-gas thermal conductivity as a function of the temperature: Nesterov et al. [64] (◆), Vargaftik and Vanicheva [65] (■), Naziev and Abasov [67] (△), and Naziev and Abasov [70] (◯), and values calculated by Eq. 14 (▬)

Full size image
Fig. 12
figure 12

Dilute-gas thermal conductivity deviations from the values obtained by the scheme of Eqs. 11 to 13, as a function of the temperature: Nesterov et al. [64] (◆), Vargaftik and Vanicheva [65] (■), Naziev and Abasov [67] (△), and Naziev and Abasov [70] (◯), and values calculated by Eq. 14 (▬)

Full size image

3.2 The Thermal Conductivity Residual Term

The thermal conductivities of pure fluids exhibit an enhancement over a large range of densities and temperatures around the critical point and become infinite at the critical point. This behavior can be described by models that produce a smooth crossover from the singular behavior of the thermal conductivity asymptotically close to the critical point to the residual values far away from the critical point [80,81,82]. The density-dependent terms for thermal conductivity can be grouped according to Eq. 9 as [Δλ(ρ,Τ) + Δλc(ρ,Τ)]. To assess the critical enhancement theoretically, we need to evaluate, in addition to the dilute-gas thermal conductivity, the residual thermal-conductivity contribution. The procedure adopted during this analysis used ODRPACK (Ref. [83]) to fit all the primary data simultaneously to the residual thermal conductivity and the critical enhancement, while maintaining the values of the dilute-gas thermal-conductivity data already obtained. The density values employed were obtained by the equation of state of Betken et al. [2]. The primary data were weighted in inverse proportion to the square of their uncertainty.

The residual thermal conductivity was represented with a polynomial in temperature and density:

$${\Delta }\lambda (\rho ,T) = \sum\limits_{i = 1}^5 {\left( {{B_{1,i}} + {B_{2,i}}(T/{T_{\text{c}}})} \right){{\left( {\rho /{\rho_{\text{c}}}} \right)}^i}}.$$
(15)

Coefficients B1,i and B2,i are shown in Table 5.

Table 5 Coefficients of Eq. 15 for the residual thermal conductivity of 1-hexene
Full size table

3.3 The Thermal Conductivity Critical Enhancement Term

The theoretically based crossover model proposed by Olchowy and Sengers [80,81,82] is complex and requires solution of a quartic system of equations in terms of complex variables. A simplified crossover model has also been proposed by Olchowy and Sengers [84]. The critical enhancement of the thermal conductivity from this simplified model is given by

$${\Delta }{\lambda_{\text{c}}} = \frac{{\rho {c_p}{R_{\text{D}}}{k_{\text{B}}}T}}{{6{\uppi }\bar \eta \xi }}\left( {\bar \Omega - {{\bar \Omega }_0}} \right),$$
(16)

with

$$\bar \Omega = \frac{2}{{\uppi }}\left[ {\left( {\frac{{{c_p} - {c_v}}}{{c_p}}} \right)\arctan \left( {{{\bar q}_{\text{D}}}\xi } \right) + \frac{{c_v}}{{c_p}}{{\bar q}_{\text{D}}}\xi } \right],$$
(17)

and

$${\bar \Omega_0} = \frac{2}{{\uppi }}\left[ {1 - \exp \left( { - \frac{1}{{{{({{\bar q}_{\text{D}}}\xi )}^{ - 1}} + {{({{\bar q}_{\text{D}}}\xi {\rho_{\text{c}}}/\rho )}^2}/3}}} \right)} \right].$$
(18)

In Eqs. 16 to 18, kB is the Boltzmann constant, \(\bar \eta\) (Pa s) is the viscosity, and cp and cv (J·kg–1·K–1) are the isobaric and isochoric specific heat obtained from the equation of state. The correlation length ξ (m) is given by

$$\xi={\xi_0}{\left({\frac{{{p_{\text{c}}}\rho}}{{{\Gamma}\rho_{\text{c}}^{2}}}}\right)^{\nu/\gamma}}{\left[{{{\left.{\frac{\partial\rho(T,\rho)}{{\partial p}}}\right|}_T}-{{\left.{\left({\frac{{{T_{{\text{ref}}}}}}{T}}\right)\frac{{\partial\rho({T_{{\text{ref}}}},\rho)}}{\partial p}}\right|}_T}}\right]^{\nu/\gamma}}.$$
(19)

As already mentioned, the coefficients B1,i and B2,i in Eq. 15 were fitted with ODRPACK (Ref. [83]) to the primary data for the thermal conductivity of 1-hexene. This crossover model requires the universal amplitude, RD = 1.02 (–), and the universal critical exponents, ν = 0.63 and γ = 1.239, and the system–dependent amplitudes Γ and ξ0. For this work, we adopted the values Γ = 0.056 (-), ξ0 = 0.235 × 10−9 m, using the universal representation of the critical enhancement of the thermal conductivity by Perkins et al. [85] To estimate the effective cutoff wavelength \(\overline{q}_{\text{D}}^{-1}(m),\) we used the method of Perkins et al.[85], and the value obtained is 6.98 × 10−10 m. The viscosity required for Eq. 16 was calculated with the correlation developed earlier in this work. The reference temperature Tref, far above the critical temperature where the critical enhancement is negligible, was calculated by Tref = (3/2) Tc [46], which for 1-hexene is 756 K. Thus, the present critical enhancement calculation is consistent with the equation of state of Betken et al. [2] and should provide reasonable estimates of the thermal conductivity critical enhancement, although the uncertainty is larger in this area.

3.4 Comparison with Data

Table 6 summarizes comparisons of the primary data with the correlation. We estimate the uncertainty (at the 95 % confidence level) for the thermal conductivity from the triple-point temperature to 620 K at pressures up to 200 MPa, to be 4 %. Uncertainties in the critical region are much larger, since the thermal conductivity approaches infinity at the critical point and is very sensitive to small changes in density. In addition, the EOS of Betkin et al. [2] has a maximum upper temperature limit of 535 K but comparisons with data indicate that the thermal conductivity correlation is valid up to 620 K using extrapolated densities from the EOS.

Table 6 Evaluation of the 1-hexene thermal-conductivity correlation for the primary data
Full size table

Figure 13 shows the percentage deviations of all primary thermal–conductivity data from the values calculated by Eqs. 9, 14 to 19, as a function of temperature. Figures 14 and 15 show the same deviations but as a function of pressure and density, respectively.

Fig. 13
figure 13

Percentage deviations of primary thermal conductivity experimental data of 1-hexene from the values calculated by the present model, Eqs. 9, 14 to 19, as a function of temperature: Zaripov et al. [62] (●), Watanabe and Kato [63] (×), Nesterov et al. [64] (+), Vargaftik and Vanicheva [65] (✶), Brykov et al. [66] (■), Naziev and Abasov [67] (◯), Naziev and Abasov [68] (△), Mukhamedzyanov and Usmanov [69 (◆), Naziev and Abasov [70] (□)

Full size image
Fig. 14
figure 14

Percentage deviations of primary thermal conductivity experimental data of 1-hexene from the values calculated by the present model, Eqs. 9, 14 to 19, as a function of pressure: Zaripov et al. [62] (●), Watanabe and Kato [63] (×), Nesterov et al. [64] (+), Vargaftik and Vanicheva [65] (✶), Brykov et al. [66] (■), Naziev and Abasov [67] (◯), Naziev and Abasov [68] (△), Mukhamedzyanov and Usmanov [69 (◆), Naziev and Abasov [70] (□)

Full size image
Fig. 15
figure 15

Percentage deviations of primary thermal conductivity experimental data of 1-hexene from the values calculated by the present model, Eqs. 9, 14 to 19, as a function of density: Zaripov et al. [62] (●), Watanabe and Kato [63] (×), Nesterov et al. [64] (+), Vargaftik and Vanicheva [65] (✶), Brykov et al. [66] (■), Naziev and Abasov [67] (◯), Naziev and Abasov [68] (△), Mukhamedzyanov and Usmanov [69 (◆), Naziev and Abasov [70] (□)

Full size image

Examining Fig. 13 (and similarly Fig. 15), one can notice that in the low temperature region the measurements of Brykov et al. [66] show a systematic trend in relation to the only other set of Naziev and Abasov [68]. This behavior has been identical in other previous reference correlations (e.g. for n-hexane [31], n-heptane [32], and n-ethanol [38]). There is no apparent explanation. In all cases, higher weight was allocated to the measurements of Naziev and Abasov [68], as they quote a lower uncertainty and their measurements cover successfully a much wider temperature and pressure range. In any case, the deviations are within the uncertainty of the current correlation.

The average absolute percent deviation (AAD) and bias for the secondary data of Tarzimanov et al. [71], are 8.09 and − 6.24 % respectively.

Figure 16 shows a plot of the thermal conductivity of 1-hexene as a function of the temperature for different pressures. The plot demonstrates the physically reasonable extrapolation behavior at pressures higher than 200 MPa and at temperatures that exceed the 620 K limit of the current measurements. As mentioned in the discussion on viscosity, the reader should be aware of the possibility of thermal decomposition [58] at high temperatures, as this correlation does not take that into account. Finally, Fig. 17 depicts the critical region as calculated by the present correlation.

Fig. 16
figure 16

The thermal conductivity of 1-hexene as a function of temperature at different pressures

Full size image
Fig. 17
figure 17

The thermal conductivity of 1-hexene as a function of density at different temperatures

Full size image

4 Recommended Values and Computer-Program Verification

4.1 Recommended Values

In Table 7, viscosity and thermal conductivity values are given along the saturation boundary, calculated from the present proposed correlation between 200 K and 500 K, while in Table 8, viscosity and thermal conductivity values are given for temperatures between 200 K and 500 K and at selected pressures. Saturation density values for selected temperatures, as well as the density values for the selected temperature and pressure are obtained from the equation of state of Betken et al. [2] The values in the tables are calculated from the given temperatures and densities according to Eqs. 1, 4 to 8 for viscosity and Eqs. 9, 14 to 19 for thermal conductivity.

Table 7 Viscosity and thermal conductivity values of 1- hexene along the saturation boundary, calculated by the present scheme
Full size table
Table 8 Viscosity and thermal conductivity values of 1-hexene at selected temperatures and pressures, calculated by the present scheme
Full size table

4.2 Computer-Program Verification

For checking computer implementations of the correlation, the following points may be used for the given T, ρ conditions: T = 300 K, ρ = 0 kg·m−3, η = 6.7237 μPa·s, and λ = 12.589 mW·m−1·K−1, while for T = 300 K, ρ = 700.0 kg m−3, η = 364.37 μPa·s, and λ = 132.139 mW·m−1·K−1 (for this point there is a very small contribution of 0.055 mW·m−1·K−1 to λ from the critical enhancement term).

5 Conclusions

New, wide-ranging correlations for the viscosity and thermal conductivity of 1-hexene based on critically evaluated experimental data were presented. Both correlations are designed to be used with a recently published equation of state [2] that extends from the triple-point temperature (133.39 K) to 535 K, at pressures up to 245 MPa. The EOS has good extrapolation behavior and we have used it slightly outside of its recommended temperature range for our correlations. The viscosity correlation is valid from the triple point to 580 K and up to 245 MPa pressure, while the thermal conductivity is valid from the triple point to 620 K and 200 MPa pressure. The estimated uncertainty (at a 95 % confidence level) for the viscosity is 2 % for the low-density gas (pressures below 0.5 MPa), and 4.8 % over the rest of the range of application. For thermal conductivity, the expanded uncertainty is estimated to be 3 % for the low-density gas and 4 % over the rest of the range.