Nonparametric estimation of population average dose-response curves using entropy balancing weights for continuous exposures

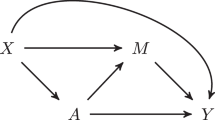
Abstract

Weighted estimators are commonly used for estimating exposure effects in observational settings to establish causal relations. These estimators have a long history of development when the exposure of interest is binary and where the weights are typically functions of an estimated propensity score. Recent developments in optimization-based estimators for constructing weights in binary exposure settings, such as those based on entropy balancing, have shown more promise in estimating treatment effects than those methods that focus on the direct estimation of the propensity score using likelihood-based methods. This paper explores recent developments of entropy balancing methods to continuous exposure settings and the estimation of population dose-response curves using nonparametric estimation combined with entropy balancing weights, focusing on factors that would be important to applied researchers in medical or health services research. The methods developed here are applied to data from a study assessing the effect of non-randomized components of an evidence-based substance use treatment program on emotional and substance use clinical outcomes.

Appendices

Appendix 1: Understanding weights and optimal covariate balance

Optimal balancing algorithms attempt to set their constraints by exploiting observable characteristics of weighted distributions and choosing a subset of these characteristics as constraints to target in their algorithms (as it may be necessary to balance an infinite number of moments to obtain weights that represent the target distribution exactly). In this appendix, we motivate the balancing constraints of these algorithms by demonstrating the effect that the weights defined earlier have on the observed distributions under weighting.

Recall the notation and setting of Sect. 2.1: a set of random variables are observed such that Y is an outcome variable, A is an exposure variable, and $\varvec{X}$ is a vector of covariates that are responsible for assigning the exposure variable; both exposure and covariates are believed to be related to the outcome Y. In the Neyman/Rubin potential outcome framework one estimation strategy attempts to find a set of weights w such that we can estimate the expectation of the potential outcome in the population represented by the distribution of $\varvec{X}$.

$$\begin{aligned} E_{\varvec{X}|A}[w Y(a) | A = a]&= E_{\varvec{X}}[Y(a)] \end{aligned}$$

It has been shown in many places (e.g., Zhu et al. (2015) and Li et al. (2018)) that one set of weights that identify the above relationship when there are non-trivial relationships among $(Y,A,\varvec{X})$ were given in Equation 1 and are of the form,

$$\begin{aligned} w \equiv w(a, \varvec{x}) = \frac{p_{A}(a)}{p_{A|\varvec{X}}(a|\varvec{x})} = \frac{p_{A}(a) }{p_{A|\varvec{X}}(a|\varvec{x})} \frac{p_{\varvec{X}}(\varvec{x})}{p_{\varvec{X}}(\varvec{x})}= \frac{p_{A}(a) p_{\varvec{X}}(\varvec{x})}{p_{A,\varvec{X}}(a,\varvec{x})} \end{aligned}$$

These weights imply certain observable characteristics in the weighted joint distribution of the treatment and covariates and provide a rationale for why an analyst should check “covariate balance” in an applied analysis. In particular, it follows from the expression above that when the weights $w(a, \varvec{x})$ are multiplied by the original joint distribution $p_{A,\varvec{X}}(a,\varvec{x})$ (under appropriate assumptions) that

$$\begin{aligned} w(a, \varvec{x}) p_{A,\varvec{X}}(a,\varvec{x})&= p_{A}(a) p_{\varvec{X}}(\varvec{x}) \end{aligned}$$

implying that the weights provide independence between A and $\varvec{X}$ in the weighted distribution.

A consequence of this identity is that for general functions $h(\cdot )$ and $g(\cdot )$, the weights yield:

$$\begin{aligned} E [ w(a, \varvec{X}) h(A) g(\varvec{X})]&= \int _{{\mathcal {A}}} \int _{{\mathcal {X}}} w(a, \varvec{x}) h(a) g(\varvec{x}) p_{A,\varvec{X}}(a,\varvec{x}) \partial a \partial \varvec{x} \\&= \int _{{\mathcal {A}}} \int _{{\mathcal {X}}} h(a) g(\varvec{x}) p_{A}(a) p_{\varvec{X}}(\varvec{x}) \partial a \partial \varvec{x} \\&= \int _{{\mathcal {A}}} h(a) p_{A}(a) d a \int _{{\mathcal {X}}} g(\varvec{x}) p_{\varvec{X}}(\varvec{x}) d \varvec{x} \\&= E[h(A)] E[g(\varvec{X})]. \end{aligned}$$

This expression yields the equations in (3) and (4) in Sect. 2.2. Specifically, to derive the expressions in (3), note that setting $h(a) = 1$ with $g(x) = x^p$ establishes $E[wX_j^p]=\mu _j^p$. The facts that $E[wA^q]=\mu _A^q$ and $E[w]=1$ are established similarly. Likewise, setting $g(x) = x^p$ and $h(a)=a^q$ yields $E[wX_j^pA^q]=\mu _j^p\mu _A^q$. This, in combination with the earlier identities, is used to established the fact that weighting eliminates covariances (including those of higher order) between $\varvec{X}$ and A as seen in (4). We have shown that weighting effectively preserves the (marginal) moment generating functions of both $\varvec{X}$ and A, and as such the marginal distributions are also maintained following weighting.

As stated at the outset, optimal balancing algorithms attempt to set their constraints by exploiting these observable characteristics in the weighted distributions and choosing a subset of constraints to target in an analysis.

Appendix 2: Derivation of optimization procedure

Consider the optimization procedure as it was defined in Sect. 2.2:

$$\begin{aligned} \begin{array}{rll} \displaystyle \min _{w} H(w,\nu ) &= \displaystyle \sum _{i =1}^N w_i \log \left( \frac{w_i}{\nu _i} \right) & \hbox {subject to} \\ 1) &\displaystyle \sum _{i =1}^N w_i (X_{ij}^p - {\hat{\mu }}_{j}^p)(A_i^q - {\hat{\mu }}_A^q) = 0 &\hbox { for each }j\hbox { and specified }p=1,2,\dots \hbox { and }q=1,2,\dots \\ 2) &\displaystyle \sum _{i =1}^N w_i (A_i^r - {\hat{\mu }}_A^r) = 0 &\hbox { for specified }r=1,2,\dots \\ 3) &\displaystyle \sum _{i =1}^N w_i (X_{ij}^s - {\hat{\mu }}_{j}^s) = 0 &\hbox { for each }j\hbox { and specified }s = 1,2,\dots \\ 4) &\displaystyle \sum _{i =1}^N w_i = 1, \qquad w_i \ge 0 \end{array} \end{aligned}$$

Here we provide a general derivation of the equations of that section.

It is possible to reformulate the above by first defining $\varvec{Z_i} = (A_i \ \varvec{X}_i)$ and letting $h_k(\varvec{Z}_i, {\hat{\mu }}_{z})$ be arbitrary functions of $A_i$ and $\varvec{X}_i$ and where ${\hat{\mu }}_{z}$ represent a vector of targets for a population of interest, e.g., ${\hat{\mu }}_z$ would be a sample estimator for the parameter $\mu _z = E_Z[\varvec{Z}]$. For example, one function from the above optimization procedure is, $h_{k'}(\varvec{Z}_i, {\hat{\mu }}_{z}) = (X_{ij}^p - {\hat{\mu }}_{j}^p)(A_i^q - {\hat{\mu }}_A^q)$. Without loss generality we can rewrite the above optimization as the following,

$$\begin{aligned} \begin{array}{rll} \displaystyle \min _{w} H(w,\nu ) = & \displaystyle \sum _{i =1}^N w_i \log \left( \frac{w_i}{\nu _i} \right) & \quad \hbox { subject to }\\ 1) &\displaystyle \sum _{i =1}^N w_i h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) = 0 & \quad \hbox { for each defined function indexed by }k \\ 2) &\displaystyle \sum _{i =1}^N w_i = 1, \qquad w_i \ge 0 \end{array} \end{aligned}$$

Using the method of Lagrange multipliers, we can augment the optimization procedure into the following new optimization,

$$\begin{aligned} \min _{w,\lambda } {\mathcal {L}}(w, \lambda )&= \sum _{i} w_i \log \left( \frac{w_i}{\nu _i} \right) + \sum _k \lambda _k \sum _{i} w_i h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + (\lambda _0 - 1)\left( \sum _{i} w_i - 1\right) \nonumber \\&= \sum _{i} w_i \log \left( \frac{w_i}{\nu _i} \right) + \sum _{i} w_i \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + (\lambda _0 - 1)\left( \sum _{i} w_i - 1\right) \end{aligned}$$

(6)

Taking derivatives with respect to each weight $w_i$, it follows that,

$$\begin{aligned} \frac{\partial }{\partial w_i} {\mathcal {L}}(w, \lambda )&= \left( 1 + \log \left( \frac{w_i}{\nu _i}\right) \right) + \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + \lambda _0 - 1 \\&= \log \left( \frac{w_i}{\nu _i}\right) + \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + \lambda _0 \end{aligned}$$

Setting to zero we have

$$\begin{aligned} w_i&\propto \nu _i \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + \lambda _0\right] \right) \end{aligned}$$

Enforcing the constraint that the weights must sum to one, it follows that

$$\begin{aligned} w_i&= \frac{\nu _i \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + \lambda _0\right] \right) }{\sum _j \nu _j \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_j, {\hat{\mu }}_{z}) + \lambda _0\right] \right) } \nonumber \\&= \frac{\nu _i \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z})\right] \right) }{\sum _j \nu _j \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_j, {\hat{\mu }}_{z}) \right] \right) } \end{aligned}$$

(7)

resulting in the closed form solution for the weights for fixed $\lambda$.

Next, to simplify notation, we redefine the weights as a parameter $\zeta _i$ divided by a normalizing constant $\zeta \equiv \sum _j \zeta _j$, i.e.,

$$\begin{aligned} w_i = \frac{\nu _i \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z})\right] \right) }{\sum _j \nu _j \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_j, {\hat{\mu }}_{z}) \right] \right) } \equiv \frac{\zeta _i}{\zeta } \end{aligned}$$

where $\zeta = \sum _j \nu _j \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_j, {\hat{\mu }}_{z}) \right] \right)$. We can also demonstrate that

$$\begin{aligned} \log (\zeta _i)&= \log (\nu _i) -\sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z})\quad \text{ implying }\\ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z})&= \log (\nu _i) - \log (\zeta _i). \end{aligned}$$

Using these two relations, we can plug the weights into the right hand side of Equation (6) (noting that $(\lambda _0 - 1)\left( \sum _{i} w_i - 1\right) = 0)$) and obtain,

$$\begin{aligned}&\sum _{i} w_i \log \left( \frac{w_i}{\nu _i} \right) + \sum _{i} w_i \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) + (\lambda _0 - 1)\left( \sum _{i} w_i - 1\right) \\&\quad = \frac{1}{\zeta }\left( \sum _i \zeta _i [\log (\zeta _i) - \log (\nu _i) - \log (\zeta )] + \sum _i \zeta _i [\log (\nu _i) - \log (\zeta _i)]) \right) \\&\quad = \frac{\log (\zeta )}{\zeta } \left( \sum _i \zeta _i\right) \\&\quad = \log (\zeta ) = \log \left( \sum _i \nu _i \exp \left( -\left[ \sum _k \lambda _k h_k(\varvec{Z}_i, {\hat{\mu }}_{z}) \right] \right) \right) . \end{aligned}$$

This final line is no longer a function of the weights and therefore can be optimized only as a function of the coefficients $\lambda _k$, the observed variables $\varvec{Z}$ and the targets ${\hat{\mu }}_z$. Finally, inserting the appropriate functions $h_k(\cdot , \cdot )$ would yield the objective function presented in Sect. 2.2.

Appendix 3: Supplemental simulation: assessing the effect of including higher marginal moment constraints for the exposure variable

This appendix provides a visualization and demonstration of the effect of enforcing constraints of higher order moments of the exposure variable of the form $\sum _{i =1}^N w_i (A_i^r - \mu _A^r) = 0$ for specified moments $r>1$. We then demonstrate how not including these constraints would affect our simulation results from the setting described in Sect. 3.3.2.

1.1 Demonstration of the role of higher exposure moments

Consider a single covariate $X\sim {\mathcal {N}}(0,1)$ and define an exposure variable such that $A = X + \epsilon$, where $\epsilon \sim {\mathcal {N}}(0,1)$. Under this generative process it follows that the marginal distribution of the exposure variable is $A\sim {\mathcal {N}}(0,2)$ and the joint distribution of the variables is $p_{A,X}(a,x) = p_{A|X}(a|x) p_{X}(x)$, which is not equal to the product distribution $p_{A}(a)p_{X}(x)$ over which inference is desired under our weighting scheme (i.e., when the weights are defined as $w = p_A(a) p_{X}(x) / p_{A|X}(a|x) p_{X}(x)$ our goal is estimating expectations over the product distribution $p_A(a) p_{X}(x)$). This is demonstrated below for a sample of $N=10,000$ drawn from this joint distribution (Fig. 7).

Fig. 7

Comparing the joint distribution of the observed data points and the product distribution where inference is desired. Panel on the left plots the sample against the contours of the joint distribution. Panel on the right plots the sample against the contours of the product distribution

In essence, the goal of the weights is to “fill-in” the underrepresented portions of the product distribution, while not distorting the marginal distributions of A, the exposure, or X, the covariate, and providing independence between A and X. Figure (8) shows weighted bivariate histograms where each bin is the sum of the weights in that bin and the colors have been normalized such that the max across all bins is the darkest color and lighter areas represent less density. The figure demonstrates the effect of weights on the distributions, where the left panel is the empirical distribution of the observations, the center panel uses estimated weights only including first-order constraints on the distribution of the exposure ($r=1$) and the right panel uses weights that have been estimated using higher-order moment constraints for the exposure distribution in the optimization procedure (in this case $r=1,2,3$).

Fig. 8

Comparing the contours of the joint distribution over which inference is desired and weighted bivariate histograms representing the weighted joint density of A and X. The bins represent the sum of the weights in that region and the color has been normalized such that each bin has been divided by the max of the sum of weights across all bins. The darkest blue represents the bin with the largest sum of weights and the smooth transition to white represents no weight in that bin (Color figure online)

Figure 8 shows that the true joint distribution has a strong relationship between A and X that is largely removed in the right two panels of the figure. However, the weighted histogram in the center panel does not completely match the target distribution (appearing to have less variance than would be necessary to fill out the contours of the plot) when only the constraint $r=1$ (i.e., no higher moments) is enforced.

To further explore this behavior, we simulated this generative process for 1,000 replications and assessed the empirical distribution of the marginal moments among the target distribution, the weighted distribution with only the first-moment of the exposure balanced, and the distribution with higher-moments of the exposure balanced. Table 5 presents these results and demonstrates that the weighting scheme that focuses only on the first moment under estimates the variances of the product distribution, while the higher moments are able to capture this feature.

Table 5 Simulation results comparing the estimated characteristics of the empirical distribution (i.e., the targets of the optimization procedure) and two weighted distributions: (1) weights estimated using entropy balancing using only the first moment constraint for the exposure variable and higher moments for X, and (2) weights estimated using entropy balancing using higher moment constraints for both the exposure variable and X

The key take-away is that by focusing only on the first moment, representation in the tails of the exposure variable in the weighted distribution is lost and may restrict the ability to estimate the entire dose-response curve (particularly when employing nonparametric estimation methods). We note that it may be clinically important to increase representation in this region of the exposure variable as these cases may be where clinicians are most interested.

1.2 Simulation: comparison of balance conditions on the exposure variable

Next, we supplement the simulation results of Sect. 3.3.2 by considering the effect of only balancing on the first moment compared to additionally balancing higher moments of the exposure.

Table 6 Results comparing the effect of including higher moments of the exposure within the balancing constraints. The left column provides the method of estimation (as described previously in the manuscript), the next column represents the number of moment constraints on the covariates that were included in the optimization, the next two columns are results balancing all higher moments of the exposure variable (up to the number of covariate moments balanced, i.e., if the max $s=2$, then the max $r = 2$). The final two columns are results restricting the algorithm to only balance the first moment of the exposure variable

Table 6 demonstrates that including higher-order moments of the exposure variable ($r>1$) reduced bias and MSE in almost all conditions. The only notable case where the MSE was lowered was when the outcome model was correctly specified (an unlikely situation in many observational settings) and four covariate moments were balanced. Finally, it is notable that balance on higher moments of the exposure also reduced bias and MSE for a mispecified linear model, which will likely be a common case in practice if using parametric modeling.

Appendix 4: Supplemental simulation: reducing sample size

In this appendix, we repeat the simulation of Sect. 3.1, but with a smaller sample size of $N=200$. Figure 9 again demonstrates the true curve and two unweighted curves in the data (a quadratic model and an unweighted linear smoother).

Fig. 9

Visualization of the distribution of exposure variable (left) and relationship between exposure and outcome (right) when $N=200$. In the left figure, the high-density region of A is highlighted and generally lies between 1.5 and 45. In the right figure, the true marginal relationship is shown in red, a simple unweighted linear smoother is shown in blue, and an unweighted quadratic estimation is provided in green (Color figure online)

The next sections summarize results.

1.1 Covariate balance

Table 7 presents the correlation and marginal balance summaries, summarized by the average and maximum value across replications, as was done in Table 2, for $N=200$. When compared with the results of Sect. 3.3.1, the balance metrics are still adequate (most correlation balance measures are small), but the magnitudes of the maximum KS-statistics are higher. This may indicate that there are difficulties in estimating dose-response curves in some cases as it is more difficult to obtain balance with smaller sample sizes.

Table 7 Summaries of balance assessments across replications. For Entropy Balancing and CBPS methods, the number to the right, i.e., (m), denotes the number of moments balanced. Correlation balance is assessed using the absolute value of the weighted correlation between each variable and the exposure variable A. The marginal balance is assessed using the Kolmogorov–Smirnov statistic between the unweighted empirical CDF and the weighted CDF. The top portion of the table are the averages of these statistics across replications and the bottom portion are the maximum across replications

1.2 Effect estimation

As noted throughout, while “perfect” covariate balance is often desired, the true goal is estimation of the outcome measure. Table 8 summarizes results of using the estimated weights in four different regression strategies; 1) a misspecified linear regression model (assuming a regression model where ${\texttt {Y}} \sim {\texttt { A}}$), 2) a correctly specified linear model (i.e., a quadratic polynomial), 3) flexible modeling using local linear regression (LOESS), and 4) flexible modeling using a basis expansion of the exposure variable A using cubic B-splines.

Table 8 Comparisons of the average bias and mean squared error between the estimated dose-response curve and the true marginal relationships on a grid $a_0 \in [1.5,45]$ and the average of the effective samples sizes for each method

The most interesting result of Table 8 is that while entropy balancing and CBPS generally reduce the effective sample size to low numbers when balancing higher moments, the performance does not dramatically suffer as a result. In fact, among the methods using LOESS to estimate the dose-response curve, the best performing weights in terms of MSE are the entropy balancing weights with three moments balanced despite an effective sample size of 62 (approximately 70 percent reduction compared with the original sample size). Future work should explore the extent to which this performance holds for entropy balancing in small samples.

1.3 Bootstrap simulation results

As in Sect. 3, we construct a simulation to explore the performance of bootstrap confidence intervals. In this section though we depart slightly from the earlier described procedure for constructing the bootstrap confidence intervals as there were computational issues with performing the split-sample procedure on bootstrapped samples with small N. In particular, in many cases the entropy balancing algorithm failed to converge due to the small sample sizes and the bootstrap requires sampling with-replacement. To overcome this, for each bootstrap sample we use the span $\zeta$ that was found on the whole sample. The results are summarized in Fig. 10.

Fig. 10

Simulation results for bootstrap confidence intervals. The upper left panel shows a single visualization of a bootstrapped confidence interval for the curve. Throughout the red curves represent the “truth” and the blue solid line represents the estimated curve; the dotted blue lines represent estimated 95% confidence intervals. The upper right panel contains the point-wise coverage of the 95% bootstrapped confidence intervals. Lower panels contain the magnitude (left) and ratio (right) of the average point-wise bootstrap standard error across the bootstrap simulations as compared to the standard error of the estimated curves obtained in this simulation. In all figures the vertical lines represent the 1st, 5th, 95th, 99th quantiles of the distribution of the exposure variable A in the high-density region (Color figure online)

The main finding is that the standard errors with this bootstrap procedure are underestimated, which is likely due to being unable to computationally perform the entire model selection procedure within each bootstrap sample. The performance of the bootstrap confidence intervals should be further investigated to fully understand their performance when combined with entropy balancing; particularly best practices for incorporating nonparametric model selection procedures with the weighting algorithm and performance in small samples.

Appendix 5: Supplemental simulation: no effect of exposure

In this Appendix, we reconsider the simulation of Sect. 3, but modify the outcome variable so that there is no effect of the exposure variable on the outcome variable, Y. To accomplish this, the data generation procedure is modified such that

$$\begin{aligned} Y&= X_1 + X_1^2 + X_2 + X_2^2 + X_1 X_2 + X_5 + \epsilon , \\ \epsilon&\sim {\mathcal {N}}(0,1) \end{aligned}$$

and all other data-generating parameters remain the same (recall that only the set of covariates $\varvec{Z}$ are observed). This implies that the marginal effect is $E[Y(a)] = 3.55$ for all $a \in {\mathcal {A}}$ and thus A has no population-level effects. Within the simulation we again use the models described in Sect. 3, but now the linear model is the correctly specified model.

A visualization of the induced relationship between exposure and outcome is shown in Fig. 11.

Fig. 11

Visualization of the distribution of exposure variable (left) and relationship between exposure and outcome (right). In the left panel, the high-density region of A is highlighted. In the right panel, the true marginal relationship is shown in red, a simple unweighted linear smoother is shown in blue, and an unweighted linear estimation is shown in green (Color figure online)

1.1 Results

1.1.1 Covariate balance

The covariate balance results are unchanged as the relationships among A and X in the data-generation are the same and the seed used for the random number generator is the same (Figs. 12, 13, 14).

1.1.2 Performance in estimating dose-response curves

The performance here is similar to the results of Sect. 3. Both entropy balancing and CBPS perform well when a high enough number of moments is balanced and all other methods perform less than satisfactory. The bootstrap confidence intervals again remain conservative, but in this case, it is observed that at certain points of the exposure distribution there is under-coverage. Future work should further investigate confidence intervals for these methods (Table 9).

Table 9 Comparisons of the average bias and mean squared error between the estimated dose-response curve and the true marginal relationships on a grid $a_0 \in [1.5,45]$ and the average of the effective samples sizes for each method

Fig. 12

Performance estimating the dose-response curve across repeated simulated samples: Local Linear Regression

Fig. 13

Performance estimating the dose-response curve across repeated simulated samples: Linear Regression - outcome is correctly modeled using linear relationship with exposure

Fig. 14

Simulation results for bootstrap confidence intervals. The upper left panel contains a single visualization of a bootstrapped confidence interval for the curve. The upper right panel contains the point-wise coverage of the 95% bootstrapped confidence intervals. Lower panels contain the magnitude (left) and ratio (right) of the average point-wise bootstrap standard error across the bootstrap simulations as compared to the standard error of the estimated curves obtained in the simulation. In all figures, the vertical lines represent the 1st, 5th, 95th, 99th quantiles of the distribution of A in the high-density region