3D Anisotropic P- and S-Mode Wavefields Separation in 3D Elastic Reverse-Time Migration

Abstract

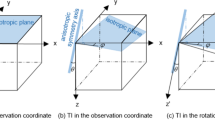
In 2D anisotropic media, non-stationary filters and low-rank approximation methods are classical strategies to compute the decomposition operators, but they suffer from expensive computational costs for 3D media. This study adopts the eigenform analysis into 3D vertical transverse isotropic (VTI) media and produces the separated vector P and S wavefields with the same amplitudes, phases, and physical units as the input elastic wavefields. We first built a 3D zero-order pseudo-Helmholtz decomposition operator by deriving the eigenvalues and eigenvectors of the 3D VTI wave equations in the wavenumber domain. The eigenvalues refer to the phase velocities of P-, SH-, and SV-wave, and the corresponding eigenvectors are pointing to their polarizations. Second, we use the pseudo-Helmholtz decomposition operator to construct a 3D anisotropic Poisson’s equation. Based on the laterally homogeneous assumption, Poisson’s equation is solved in the mixed domain $z - k_{x} - k_{y}$, where $k_{x}$, $k_{y}$, and $z$ denote the horizontal wavenumbers and depth, respectively. Third, we obtain the vector P and S wavefields using the proposed 3D pseudo-Helmholtz decomposition operator in the space domain. Lastly, 3D PP and PS images are calculated with a dot-product imaging condition. The anisotropic amplitude versus offset (AVO) responses of the 3D elastic reverse-time migration (ERTM) images are also validated by analytical solutions (Ruger’s equations). Our proposed 3D pseudo-Helmholtz decomposition operator degrades to a gradient operator satisfying isotropic media conditions. In addition, the method is easy to extend into 3D due to its high-efficiency cost. Several numerical examples with large shear anisotropy are selected to demonstrate the feasibility of our proposed pseudo-Helmholtz decomposition method in 3D applications.

Appendix

Assuming the eigenvalue of the matrix ${\text{A}}$ is $\lambda$ with the corresponding eigenvector ($x_{1} ,x_{2} ,x_{3}$), so we have

$$ \begin{gathered} \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)x_{1} + \left( {c_{11} - c_{66} } \right)k_{x} k_{y} x_{2} + \left( {c_{13} + c_{44} } \right)k_{x} k_{z} x_{3} = \lambda x_{1} , \hfill \\ \left( {c_{11} - c_{66} } \right)k_{x} k_{y} x_{1} + \left( {c_{66} k_{x}^{2} + c_{11} k_{y}^{2} + c_{44} k_{z}^{2} } \right)x_{2} + \left( {c_{13} + c_{44} } \right)k_{y} k_{z} x_{3} = \lambda x_{2} , \hfill \\ \left( {c_{13} + c_{44} } \right)k_{x} k_{z} x_{1} + \left( {c_{13} + c_{44} } \right)k_{y} k_{z} x_{2} + \left( {c_{44} k_{x}^{2} + c_{44} k_{y}^{2} + c_{33} k_{z}^{2} } \right)x_{3} = \lambda x_{3} . \hfill \\ \end{gathered} $$

(A1)

For the first equation of (A1), if set $x_{3} = 1$, we obtain

$$ x_{1} = \frac{{\left( {c_{13} + c_{44} } \right)k_{x} k_{z} + \left( {c_{11} - c_{66} } \right)k_{x} k_{y} x_{2} }}{{\lambda_{3} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)}}. $$

(A2)

Then inserting Eq. (A2) into the second equation of (A1), we obtain

$$ x_{2} = \frac{{\left( {c_{13} + c_{44} } \right)\left( {c_{11} - c_{66} } \right)k_{x}^{2} k_{y} k_{z} + \left[ {\lambda_{3} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left( {c_{13} + c_{44} } \right)k_{z} k_{y} }}{{\left[ {\lambda_{3} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left[ {\lambda_{3} - \left( {c_{66} k_{x}^{2} + c_{11} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right] - \left( {c_{11} - c_{66} } \right)^{2} k_{x}^{2} k_{y}^{2} }}. $$

(A3)

Finally, substituting the knowing eigenvalue $\lambda_{3}$ into Eqs. (A2) and (A3), we have the eigenvector $\hat{a}_{3}$.

If set $x_{2} = 1$, we obtain

$$ x_{1} = \frac{{\left( {c_{11} - c_{66} } \right)k_{x} k_{y} + \left( {c_{13} + c_{44} } \right)k_{x} k_{z} x_{3} }}{{\lambda_{2} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)}}. $$

(A4)

Then inserting Eq. (A4) into the third equation of (A1), we obtain

$$ x_{3} = \frac{{\left( {c_{13} + c_{44} } \right)\left( {c_{11} - c_{66} } \right)k_{x}^{2} k_{y} k_{z} + \left[ {\lambda_{2} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left( {c_{13} + c_{44} } \right)k_{z} k_{y} }}{{\left[ {\lambda_{2} - \left( {c_{11} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left[ {\lambda_{2} - \left( {c_{44} k_{x}^{2} + c_{44} k_{y}^{2} + c_{33} k_{z}^{2} } \right)} \right] - \left( {c_{13} + c_{44} } \right)^{2} k_{x}^{2} k_{z}^{2} }}. $$

(A5)

After substituting $\lambda_{2}$ into Eqs. (A4) and (A5), we have the eigenvector ${\hat{\text{a}}}_{2}$.

If set $x_{1} = 1$ for the second part equation of (A1), we obtain

$$ x_{2} = \frac{{\left( {c_{11} - c_{66} } \right)k_{x} k_{y} + \left( {c_{13} + c_{44} } \right)k_{y} k_{z} x_{3} }}{{\lambda_{1} - \left( {c_{66} k_{x}^{2} + c_{11} k_{y}^{2} + c_{44} k_{z}^{2} } \right)}}. $$

(A6)

And inserting Eq. (A6) into the third part of Eq. (A1), we obtain

$$ x_{3} = \frac{{\left( {c_{13} + c_{44} } \right)\left( {c_{11} - c_{66} } \right)k_{x} k_{y}^{2} k_{z} + \left[ {\lambda_{1} - \left( {c_{66} k_{x}^{2} + c_{11} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left( {c_{13} + c_{44} } \right)k_{x} k_{z} }}{{\left[ {\lambda_{1} - \left( {c_{66} k_{x}^{2} + c_{11} k_{y}^{2} + c_{44} k_{z}^{2} } \right)} \right]\left[ {\lambda_{1} - \left( {c_{44} k_{x}^{2} + c_{44} k_{y}^{2} + c_{33} k_{z}^{2} } \right)} \right] - \left( {c_{13} + c_{44} } \right)^{2} k_{y}^{2} k_{z}^{2} }}. $$

(A7)

In the same way, we have the eigenvector ${\hat{\text{a}}}_{1}$ with $\lambda_{1}$.

The eigenvalues $\lambda_{1}$, $\lambda_{2}$, and $\lambda_{3}$ of Eq. (A1) is determined by $\left| {\lambda E - {\text{A}}} \right| = 0$ being rewritten as

$$ \left| {\begin{array}{*{20}c} {\lambda - c_{11} k_{x}^{2} - c_{66} k_{y}^{2} - c_{44} k_{z}^{2} } & { - \left( {c_{11} - c_{66} } \right)k_{x} k_{y} } & { - \left( {c_{13} + c_{44} } \right)k_{x} k_{z} } \\ { - \left( {c_{11} - c_{66} } \right)k_{x} k_{y} } & {\lambda - c_{66} k_{x}^{2} - c_{11} k_{y}^{2} - c_{44} k_{z}^{2} } & { - \left( {c_{13} + c_{44} } \right)k_{y} k_{z} } \\ { - \left( {c_{13} + c_{44} } \right)k_{x} k_{z} } & { - \left( {c_{13} + c_{44} } \right)k_{y} k_{z} } & {\lambda - c_{44} k_{x}^{2} - c_{44} k_{y}^{2} - c_{33} k_{z}^{2} } \\ \end{array} } \right| = 0. $$

(A8)

Solving Eq. (A8), then the eigenvalues are

$$ \begin{aligned} \lambda_{2} = & c_{66} k_{x}^{2} + c_{66} k_{y}^{2} + c_{44} k_{z}^{2} , \\ \lambda_{1,3} = & \frac{{\left( {c_{44} + c_{11} } \right)k_{x}^{2} + \left( {c_{44} + c_{11} } \right)k_{y}^{2} + \left( {c_{33} + c_{44} } \right)k_{z}^{2} }}{2} \pm \frac{{\left( {c_{11} - c_{44} } \right)k_{x}^{2} + \left( {c_{11} - c_{44} } \right)k_{y}^{2} + \left( {c_{33} - c_{44} } \right)k_{z}^{2} }}{2}, \\ \times \sqrt {1 + \frac{{4\left( {c_{44} c_{11} - c_{11} c_{33} + c_{33} c_{44} + c_{13}^{2} + 2c_{13} c_{44} } \right)\left( {k_{x}^{2} + k_{y}^{2} } \right)k_{z}^{2} }}{{\left[ {\left( {c_{11} - c_{44} } \right)k_{x}^{2} + \left( {c_{11} - c_{44} } \right)k_{y}^{2} + \left( {c_{33} - c_{44} } \right)k_{z}^{2} } \right]^{2} }}} \\ \end{aligned} $$

(A9)

Replacing the stiffness coefficients with the Thomsen parameters, Eq. (A9) can be simplified as

$$ \begin{aligned} \lambda_{2} = & \rho v_{s}^{2} \left[ {\left( {1 + 2\gamma } \right)k_{x}^{2} + \left( {1 + 2\gamma } \right)k_{y}^{2} + k_{z}^{2} } \right], \\ \lambda_{1,3} = & \frac{{\left[ {\left( {1 + 2\varepsilon } \right)v_{p}^{2} + v_{s}^{2} } \right]k_{x}^{2} + \left[ {\left( {1 + 2\varepsilon } \right)v_{p}^{2} + v_{s}^{2} } \right]k_{y}^{2} + \left( {v_{p}^{2} + v_{s}^{2} } \right)k_{z}^{2} }}{2}, \\ \pm \rho \frac{{\left[ {\left( {1 + 2\varepsilon } \right)v_{p}^{2} - v_{s}^{2} } \right]k_{x}^{2} + \left[ {\left( {1 + 2\varepsilon } \right)v_{p}^{2} - v_{s}^{2} } \right]k_{y}^{2} + \left( {v_{p}^{2} - v_{s}^{2} } \right)k_{z}^{2} }}{2}, \\ \times \sqrt {1 - \frac{{8\left( {\varepsilon - \delta } \right)v_{p}^{2} \left( {v_{p}^{2} - v_{s}^{2} } \right)\left( {k_{x}^{2} + k_{y}^{2} } \right)k_{z}^{2} }}{{\left[ {\left( {\left( {1 + 2\varepsilon } \right)v_{p}^{2} - v_{s}^{2} } \right)k_{x}^{2} + \left( {\left( {1 + 2\varepsilon } \right)v_{p}^{2} - v_{s}^{2} } \right)k_{y}^{2} + \left( {v_{p}^{2} - v_{s}^{2} } \right)k_{z}^{2} } \right]^{2} }}} \\ \end{aligned} $$

(A10)

Based on the weak anisotropy hypothesis, we approximate the square-root term using the first-order Taylor expansion. Eq. (A10) can be simplified as Eq. (4).