1 Introduction

Stereographic projection is the classical approach for the analysis of rock discontinuities. The concept and the graphical methods are widely used in rock engineering education in the classrooms to illustrate the orientation of planes of discontinuity, occurrence of failures, ect. For this purpose, the graphical approach with tracing paper has proved its advantage in many textbooks (Goodman et al 1989; Jaeger et al 2009; Sivakugan et al 2013). Nevertheless, the procedure using tracing papers has some inaccuracy due to several reasons: (a) the tack is not pinned at the centre of the stereonet; (b) the rotation of the tracing paper enlarges the hole of the tack, allowing the tracing paper to move; (c) the traces with pencil are not close; (d) the stereonet size on A4 paper is too small; and (e) other human errors. The authorial practice showed that a tolerance of \(3^\circ\) is frequently required.

To deal with a large number of discontinuities, the common practice is to use a computer program, such as Stereonet - a freeware (Allmendinger 2015), Dips - a commercial program (Rocscience 2022), and Orient - a Github project (Vollmer 2023). Although some measuring tools are provided to calculate intersection and angles (Rocscience 2022), rotation of net is not facilitated. Some programs, such as Stereonet 11 (Allmendinger 2023) and Visible Geology (Seequent 2023) provide rotatable 3D view, where the whole system is rotated collectively. This is different from the traditional graphical solution, where only the tracing paper is rotated. As a sequence, many hand solutions for practical problems are not digitised. For example, how does one predict a discontinuity if some features of its intersection with two slopes can be observed? Solution for those problems requires some graphical drawing with computer mouse or stylus, which in turn is less accurate. The authorial practice showed again the tolerance is in the order of \(3^\circ\), given the zooming feature works well.

Although the \(3^\circ\) tolerance is not very significant in rock mechanics, the error can accumulate to something substantial if the solution includes many steps. This technical note is to develop simple analytical solutions for some practical problems. The suggested analytical formulations can be adopted by engineering programs to develop tools for rock engineers. It is obvious that the current graphical solutions with tracing papers are not suitable when dealing with massive data in rock mechanics.

2 Theoretical Framework

Basis of many computational tools for stereographic projection is the vector forms (Rocscience 2022). However, this mathematical foundation is often omitted in many rock mechanics books including Sivakugan et al (2013) and Lisle and Leyshon (2004), possibly to give pages for operation with the Wuff net. Several instructions used polar coordinate system to describe the hemispherical projection Priest (1985, 1993), which may be difficult for vector operation. This section is devoted to give an insight into the mathematical foundation.

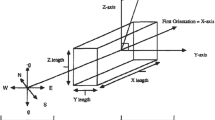
In stereographic projection with a unit sphere, a planar discontinuity is conventionally identified by two angles: dip direction \(\alpha\) and dip angle \(\psi\). This representation is not suitable for mathematical equations in vector form. Hence, the two angles (\(\alpha\), \(\psi\)) which define a plane will be converted to Cartesian coordinates of the pole point a, b, and c (Figure 1) so that with all points on the plane:

$$\begin{aligned} ax + by + cz = 0 \end{aligned}$$
(1)
Fig. 1
figure 1

Plane parameters

Full size image

The converted parameters can be calculated as (Priest 1985):

$$\begin{aligned} {\left\{ \begin{array}{ll} a = &{} -sin\alpha * sin\psi \\ b = &{} -cos\alpha * sin\psi \\ c = &{} -cos\psi \\ \end{array}\right. } \end{aligned}$$
(2)

Similarly, a line (\(\alpha\), \(\psi\)) can also be presented by parameters of its unit vector (Priest 1985):

$$\begin{aligned} {\left\{ \begin{array}{ll} a = &{} sin\alpha * cos\psi \\ b = &{} cos\alpha * cos\psi \\ c = &{} -sin\psi \\ \end{array}\right. } \end{aligned}$$
(3)

2.1 Angle Between Two Intersecting Planes

The angle \(\theta\) between two intersecting planes (\(\alpha _1\), \(\psi _1\)) and (\(\alpha _2\), \(\psi _2\)) can be calculated as the angle between two normal vectors. This angle is estimated as the dot product of the two vectors as their length is unit length.

$$\begin{aligned} cos\theta = sin\alpha _1 * sin\psi _1*sin\alpha _2 * sin\psi _2 + cos\alpha _1 * sin\psi _1*cos\alpha _2 * sin\psi _2 + cos\psi _1*cos\psi _2 \end{aligned}$$
(4)

Note that, there is another solution of \(180^\circ-\theta\).

Example 1

A geotechnical investigation on a foundation found two major joint sets with dip direction and dip angle are (\(78^\circ, 45^\circ\)) and (\(256^\circ, 70^\circ\)), respectively. Identify the angle between these joint sets for mass calculation.

Graphical approach

  • Draw two great circles for two planes with the given dip directions and dip angles.

  • For each plane, rotate the tracing paper so that the plane trends to the East and count \(90^\circ\) from the dip to mark the poles.

  • Rotate the tracing paper so that two poles are on the same great circle.

  • Use small circles to count the angle between two planes.

Analytical approach

Using Eq. 4\( sin78^{\circ } *sin45^{\circ } *sin256^{\circ } *sin70^{\circ } + cos78^{\circ } *sin45^{\circ } *cos256^{\circ } *sin70^{\circ } + cos45^{\circ } *cos70^{\circ } = - 0.42221\theta = arcos( - 0.4221) = 114.97^{\circ } \) (with the second solution being \(65.03^\circ\))

2.2 Dip and Dip Angle of the Intersection Line Between Two Planes

The intersection line (\(\alpha ,\psi\)) between two planes (\(\alpha _1,\psi _1\)) and (\(\alpha _2,\psi _2\)) is calculated by the cross product of two normal vectors.

$$\begin{aligned} {\left\{ \begin{array}{ll} a= &{} cos\alpha _1*sin\psi _1*cos\psi _2 - cos\psi _1*cos\alpha _2*sin\psi _2\\ b= &{} cos\psi _1*sin\alpha _2*sin\psi _2 - sin\alpha _1*sin\psi _1*cos\psi _2\\ c= &{} sin\alpha _1*sin\psi _1*cos\alpha _2*sin\psi _2 - cos\alpha _1*sin\psi _1*sin\alpha _2*sin\psi _2 \end{array}\right. } \end{aligned}$$
(5)

If the intersection vector points up (\(c>0\)), it must be flipped to the opposite direction, i.e., sign of a, b,  and c must be changed. Then, the dip angle and dip direction can be converted as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha = &{} arctan2 \frac{b}{a}\\ \psi = &{} arctan\frac{-c}{\sqrt{a^2+b^2}} \end{array}\right. } \end{aligned}$$
(6)

Note that, arctan2 is a function that returns the angle in range from \(0^\circ\) to \(360^\circ\). If \(\alpha\) is negative, it must add \(360^\circ\) to be positive.

Example 2a A geotechnical investigation on a slope found two joint sets with dip direction and dip angle are (\(42^\circ, 52^\circ\)) and (\(124^\circ, 70^\circ\)), respectively. Identify the intersection line for wedge slide analysis.

Graphical Approach

  • Draw two great circles for two planes with the given dip directions and dip angles.

  • Draw a line from the centre point to the intersection point

  • Rotate the intersection line to the East to count the dip angle.

  • Mark the East and rotate back to the original position to find the dip direction.

Analytical approach

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} a= &{} cos42^\circ*sin52^\circ*cos70^\circ - cos52^\circ*cos124^\circ*sin70^\circ = 0.5238\\ b= &{} cos52^\circ*sin124^\circ*sin70^\circ - sin42^\circ*sin52^\circ*cos70^\circ = 0.2993\\ c= &{} sin42^\circ*sin52^\circ*cos124^\circ*sin70^\circ - cos42^\circ*sin52^\circ*sin124^\circ*sin70^\circ = -0.7333 \end{array}\right. }\\{} & {} {\left\{ \begin{array}{ll} \alpha = &{} arctan2 \frac{0.2993}{0.5238} = 60.25^\circ\\ \psi = &{} arctan\frac{0.7333}{\sqrt{0.5238^2+0.2993^2}} = 50.55^\circ \end{array}\right. } \end{aligned}$$

Example 2b After the construction of a highway over the slope in Example 2a, another investigation was undertaken. It found a new joint set (\(245^\circ,60^\circ\)). identify the intersection lines with the first plane (\(42^\circ, 52^\circ\)).

Graphical Approach

Repeat the process in example 2a for new pairs of joints

Analytical Approach

$$\begin{aligned}{\left\{ \begin{array}{ll} a= &{} cos42^\circ*sin52^\circ*cos60^\circ - cos52^\circ*cos245^\circ*sin60^\circ = 0.5181\\ b= &{} cos52^\circ*sin245^\circ*sin60^\circ - sin42^\circ*sin52^\circ*cos60^\circ = -0.7469\\ c= &{} sin42^\circ*sin52^\circ*cos245^\circ*sin60^\circ - cos42^\circ*sin52^\circ*sin245^\circ*sin60^\circ = 0.2665 \end{array}\right. } \end{aligned}$$

As c is negative, the vector must be flipped to the opposite direction.

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha = &{} arctan2 \frac{0.7469}{-0.5181} = -34.75^\circ\\ \psi = &{} arctan\frac{0.2665}{\sqrt{-0.5181^2+0.7469^2}} = 16.35^\circ \end{array}\right. } \end{aligned}$$

As \(\alpha\) is negative, the result must add \(360^\circ\). Hence the intersection line is (\(325.25^\circ,16.35^\circ\)). Note that, the dip direction and dip angle can be converted first and flipped later.

Calculation in Section 2 may be done with current computational tools. In this paper, a comparison with Dips (Rocscience 2022) was undertaken as an example (Figure 2). Although the scientific basis is not explicit in the manuals (Rocscience 2022), the nuance to Section 2 should not be significant. However, as there is lack of rotation and snap** feature, the prediction of fracture need to be digitised.

Fig. 2
figure 2

Computer solutions: Example 1 (left) and Example 2 (middle and right)

Full size image

3 Identification of a Fracture with Traces on Two Slopes

A frequent problem for rock engineering is the identification of a fracture with some observed evidence. If traces are observed from two adjacent slopes (\(\alpha _1, \psi _1\)) and (\(\alpha _2, \psi _2\)), there may be a persistent fracture (\(\alpha , \psi\)) connecting them. In this situation a confirming investigation is undertaken by drilling several boreholes. If the fracture is predicted with certainty, just one borehole is needed for confirmation. The predicting process includes two steps. In the first step, the two intersection lines (\(\alpha _3, \psi _3\)) and (\(\alpha _4, \psi _4\))are identified. If the dip direction \(\alpha _3\) of a trace is known via geo-compass, the dip angle \(\psi _3\) of that trace on a slope plane (\(\alpha _1, \psi _1\)) is estimated by submitting the line end coordinates to the Eq. 2. In a nutshell, the dot product of parameters in Eqs. 2 and 3 must be 0.

$$\begin{aligned} -sin\alpha _1 * sin\psi _1*sin\alpha _3 * cos\psi _3 - cos\alpha _1 * sin\psi _1 * cos\alpha _3 * cos\psi _3 + cos\psi _1*sin\psi _3 =0 \end{aligned}$$
(7)

Or

$$\begin{aligned} \psi _3 = arctan\frac{sin\alpha _1 * sin\psi _1*sin\alpha _3 + cos\alpha _1 * sin\psi _1 * cos\alpha _3}{cos\psi _1} \end{aligned}$$
(8)

Note that, \(\psi _3\) takes only positive values and is less than \(90^\circ\). Hence, if \(\psi _3\) is negative, it must be converted to the absolute value.

In case \(\psi _3\) is known, \(\alpha _3\) can be estimated through several substeps. Eq. 7 becomes:

$$\begin{aligned}{} & {} sin\alpha _1 * sin\psi _1*sin\alpha _3 * cos\psi _3 + cos\alpha _1 * sin\psi _1 * \nonumber \\{} & {} \quad cos\alpha _3 * cos\psi _3 = cos\psi _1*sin\psi _3 \end{aligned}$$
(9)

Then, let

$$\begin{aligned} {\left\{ \begin{array}{ll} A &{} = sin\alpha _1 * sin\psi _1* cos\psi _3 \\ B &{} = cos\alpha _1 * sin\psi _1 * cos\psi _3 \\ C &{} = cos\psi _1*sin\psi _3 \end{array}\right. } \end{aligned}$$
(10)

Equation 9 becomes

$$\begin{aligned} A*sin\alpha _3 + B*cos\alpha _3 =C \end{aligned}$$
(11)

Now, let

$$\begin{aligned} \beta = arcsin\frac{A}{\sqrt{A^2+B^2}}=arccos\frac{B}{\sqrt{A^2+B^2}}=arctan\frac{A}{B} \end{aligned}$$
(12)

Divide both sides of Eq. 11 on \(\sqrt{A^2+B^2}\) to get

$$\begin{aligned} sin\beta *sin\alpha _3 + cos\beta *cos\alpha _3 = \frac{C}{\sqrt{A^2+B^2}} \end{aligned}$$
(13)

Or

$$\begin{aligned} \cos (\alpha _3-\beta )=\frac{C}{\sqrt{A^2+B^2}} \end{aligned}$$
(14)

Hence,

$$\begin{aligned} \alpha _3 =arctan\frac{A}{B}\pm arccos \frac{C}{\sqrt{A^2+B^2}} \pm \pi \end{aligned}$$
(15)

Although Eq. 15 could have four answers, two of them can be eliminated automatically because they point to the other side of the stereonet. The selection from the remaining two answers may need additional information. Note that, dip direction takes value from \(0^\circ\) to \(360^\circ\). Hence, if the result is negative or larger than \(360^\circ\), it must add/subtract \(360^\circ\) to be back to the range.

In the second step, the normal vector to the fracture plane (\(\alpha , \psi\)) is estimated as the cross product of the two intersection lines (\(\alpha _3, \psi _3\)) and (\(\alpha _4, \psi _4\)), calculated in the first step.

$$\begin{aligned} {\left\{ \begin{array}{ll} a= &{} cos\alpha _3*cos\psi _3*(-sin\psi _4) - (-sin\psi _3)*cos\alpha _4*cos\psi _4\\ b= &{} (-sin\psi _3)*sin\alpha _4*cos\psi _4 - sin\alpha _3*cos\psi _3*(-sin\psi _4)\\ c= &{} sin\alpha _3*cos\psi _3*cos\alpha _4*cos\psi _4 - cos\alpha _3*cos\psi _3*sin\alpha _4*cos\psi _4 \end{array}\right. } \end{aligned}$$
(16)

Or

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha = arctan2\frac{b}{a}\\ \psi = arctan\frac{\sqrt{a^2+b^2}}{c} \end{array}\right. } \end{aligned}$$
(17)

As stated above, the normal vector can point up. In this case, it must be flipped.

Fig. 3
figure 3

Observed traces on two adjacent slopes

Full size image

Example 3

A rock slope was cut for a proposed construction (Figure 3). However, traces of a possible joint were observed at both sides of the opening. Identify the possible joint.

Graphical Approach

  • Draw two great circles to illustrate the two sides

  • Draw intersection lines to the given directions. Estimate two intersection points with the great circle of the respective side.

  • Rotate the tracing paper until the two points are allocated on the same great circle.

  • Draw the great circle of the possible joint. Count the dip angle and mark to estimate the dip direction.

Analytical Approach

Identify the dip angle of the trace to \(55^\circ\), using Eq. 8\(\psi _3 = arctan\frac{sin135^\circ * sin50^\circ *sin55^\circ + cos135^\circ * sin50^\circ * cos55^\circ }{cos50^\circ } = 11.69^\circ\) Similarly, identify the dip angle of the trace to \(320^\circ\) \(\psi _4 = arctan\frac{sin45^\circ * sin62^\circ *sin320^\circ + cos45^\circ * sin62^\circ * cos320^\circ }{cos62^\circ } = 9.31^\circ\)

Build the plane of the possible joint from the two intersection lines (\(55^\circ,11.69^\circ\)) and (\(320^\circ,9.31^\circ\)), using Eqs. 16 and 17

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} a&{}= cos55^\circ*cos11.69^\circ*(-sin9.31^\circ) - (-sin11.69^\circ)*cos320^\circ*cos9.31^\circ = 0.0623\\ b&{}= (-sin11.69^\circ)*sin320^\circ*cos9.31^\circ - sin55^\circ*cos11.69^\circ*(-sin9.31^\circ) = 0.2583\\ c&{}=sin55^\circ*cos11.69^\circ*cos320^\circ*cos9.31^\circ - cos55^\circ*cos11.69^\circ*sin320^\circ*cos9.31^\circ \\ &{}= 0.9627 \end{array}\right. } \\{} & {} {\left\{ \begin{array}{ll} \alpha = arctan2\frac{0.2583}{0.0623} = 13.57^\circ\\ \psi = arctan\frac{\sqrt{0.0623^2+0.2583^2}}{0.9627}=15.43^\circ \end{array}\right. } \end{aligned}$$

4 Identification of a Fracture with a Trace on one Slope

A visual inspection on a slope (\(\alpha _1, \psi _1\)) can find traces of discontinuities, which daylight on the slope. If there is a trace (\(\alpha _2, \psi _2\)), there may be a persistent fracture (\(\alpha , \psi\)) inside the rock mass. This is a typical problem, which requires identification of a fracture plane, if a line is known. Note that, if one data \(\alpha _2\) or \(\psi _2\) is missing, it can be calculated with Eq. 15 or 8. Based on the geometry of the trace, the dip direction \(\alpha\) or dip angle \(\psi\) of the fracture plane can be identified. In case \(\alpha\) is known, \(\psi\) is estimated by submitting coordinates of line end to the plane equation, which is the dot product of Eqs. 2 and 3 into Eq. 7:

$$\begin{aligned}{} & {} tan\psi \nonumber \\{} & {} \quad = \frac{sin\psi _2}{sin\alpha *sin\alpha _2*sin\psi _2+cos\alpha *cos\alpha _2*sin\psi _2} \end{aligned}$$
(18)

In case \(\psi\) is known, the dip direction \(\alpha\) can be estimated via a similar process to Eq. 9 - 15. Because this problem can have several solutions. Additional information may be required to limit the options. For example, the fracture trends to the Northern half or Southern half of the hemisphere projection.

Example 4

A visual investigation for an underground mine slope (\(250^\circ,60^\circ\)) showed that there might be an existing joint set. When a geo-compass was placed in the rock aperture, the dip angle was read from side inclinator at \(52^\circ\). However, the dip direction could not be estimated as there is not enough space to look at the geo-compass from the top. Nevertheless, it seems that the joint set trends to the Northern side. The trace on the slope has dip angle of \(44^\circ\) and runs to the Northern side too. Identify the new joint set.

Graphical Approach

  • Draw a great circle for the mine slope (\(250^\circ,60^\circ\)).

  • Draw a circle at the dip of \(44^\circ\). This circle intersects the slope at two points.

  • Pick up the point in the Northern half.

  • Rotate the tracing paper so that the point is on the great circle with dip angle of \(52^\circ\).

  • There will be four possible answers. Two answers are just the duplication and can be eliminated. With the remaining two answers, pick up the great circle, which trends to the Northern half.

  • Mark the dip and rotate back to the original position to count the dip direction.

Analytical Approach

Using Eqs. 9–15, identify the dip direction of the intersection line. \({\left\{ \begin{array}{ll} A &{} = sin250^\circ * sin60^\circ * cos44^\circ = -0.5854 \\ B &{} = cos250^\circ * sin60^\circ * cos44^\circ = -0.2131 \\ C &{} = cos60^\circ*sin44^\circ = 0.3473 \end{array}\right. }\) As C is positive, it must be flipped to the opposite direction. Then, the dip direction of the trace can be \(\alpha _2 =arctan\frac{0.5854}{0.2131}\pm arccos \frac{-0.3473}{\sqrt{0.5854^2+0.2131^2}} \pm \pi = {\left\{ \begin{array}{ll} 13.88^\circ \\ 126.11^\circ \\ 193.88^\circ\\ 306.11^\circ \end{array}\right. }\)

As the slope goes to \(250^\circ\), the dip direction of the line should be within \(250^\circ \pm 90^\circ\). Then, \(13.88^\circ\) and \(126.11^\circ\) are eliminated. Besides, the trace goes to the Northern half, so \(\alpha _2 = 306.11^\circ\). Using Eqs. 9–15 again, identify the dip direction of the join set. \({\left\{ \begin{array}{ll} A &{} = sin52^\circ * sin306.11^\circ * cos44^\circ = -0.4579 \\ B &{} = sin52^\circ * cos306.11^\circ * cos44^\circ = 0.3341 \\ C &{} = cos52^\circ * sin44^\circ = 0.4277 \end{array}\right. }\)

As C is positive, it must be flipped to the opposite direction. Then, the dip direction of the possible joint can be \(\alpha _2 =arctan\frac{0.4579}{-0.3341}\pm arccos \frac{-0.4277}{\sqrt{0.4579^2+(-0.3341)^2}} \pm \pi = {\left\{ \begin{array}{ll} 85.10^\circ \\ 167.13^\circ \\ 265.10^\circ\\ 347.13^\circ \end{array}\right. }\) As the trace goes to \(306.11^\circ\), the dip direction of the line should be within \(306.11^\circ \pm 90^\circ\). Then, \(85.10^\circ\) and \(167.13^\circ\) are eliminated. Besides, the joint set trends to the Northern half, so \(\alpha = 347.13^\circ\). The possible joint set is (\(347.13^\circ, 52^\circ\))

5 Dealing with Multiple Data from Scan

One of the biggest advantages of the new method over the traditional stereonet is the ability to deal with massive data, which can be obtained by terrestrial scan (Bolkas et al 2018; Vlachopoulos et al 2020; To 2019). When there are more than ten planes, the great circles on the stereonet are overcrowded. Then, the dip mode must be switched to polar mode, where any plane can be presented by a single polar point. To ease the analysis, computer programs often use colour code to indicate the concentration of points in a certain region on the stereonet and provide a mean value of a set of planes(Vazaios et al 2017). Further graphical operation will be done with the mean set plane. However, as the rotation and snap features are not well digitised yet, activities in section 3, 4 may not be done with stereonet on computer. Rock engineers must use tracing paper to identify the potential fracture from the mean set planes. Thereby, no probability could be estimated. Meanwhile, the new analytical approach can easily compute with large sets of discontinuities and provide some statistics on the possible fracture.

Fig. 4
figure 4

Illustration of data from a terrestrial scan

Full size image

Example 5

A terrestrial scan with LiDaR at a rare earth deposit found traces of a potential fracture on two slopes (see data in Appendix). Calculate the dip angle and dip direction of the potential failure.

Graphical Approach

Can be done as in example 3. However, the hand solution requires way too much work. Mean set planes estimated with Dip (Figure 4) are (\(54.05^\circ, 67.11^\circ\)) and (\(86.61^\circ, 89.59^\circ\)). The estimation of potential fracture from the mean set planes as guided in graphical solution in Example 3 is (\(143^\circ, 89^\circ\)).

Analytical Approach

The analytical approach can be done easily with any computational tool, like spreadsheet or MATLAB. An example of data analysis is shown on Figure 5. Although the analysis on dip angle seems close to the graphical solution, the analysis on dip direction shows the advantage of the analytical method.

  • The data bin with highest count is near \(117^\circ\) degree, which is the far left bin. It is obviously far away from the mean value. In fact, the data bin of \(143^\circ\) as estimated with graphical solution has no data, that is, no possible fracture with this dip direction.

  • There is a significant count of possible planes, which trend to the other side. This shows a high potential of toppling, which the graphical solution with mean set planes cannot show.

Fig. 5
figure 5

Analytical results

Full size image

6 Conclusion

The technical note has presented analytical solutions for fracture prediction without stereonet. This helps to reduce errors in the graphical approach. Besides, the prediction can be done automatically with spreadsheets or computer programs. If no additional information is input, the problems can have more than one feasible solution. This reflects the true possibilities.

The new approach does not aim to replace the graphical solution, but to enhance it in modern computational tools, where the rotation and snap features are not available yet. The implementation may have significant impact on research in geoscience, geology, and geotechnical engineering as it can deal effectively with massive data from rock surface or underground scans.