The impact of imposed Couette flow on the stability of pressure-driven flows over porous surfaces

Abstract

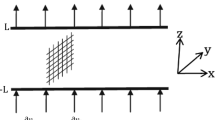
We present linear stability analysis of a pressure-driven flow in a fluid-layer overlaying porous media in the presence of a Couette component introduced by an upper impermeable wall. We model the flow dynamics in the porous media by the Brinkman equation and couple it with the Navier–Stokes equation for flows in the fluid-layer. The effect of the Couette flow component on flow stability is discussed in detail with varying the permeability and the relative thickness of the fluid to porous layers. The results show that the effect changes from destabilizing to stabilizing at a certain velocity of the upper wall. This velocity, called the cutoff velocity, is highly dependent on the porous medium characteristics. The cutoff velocity drops as the permeability of the porous surface decreases or the fluid layer thickness increases. Imposing a Couette flow shifts the instability mode from fluid mode to porous mode due to generation of vortices at the interface when the porous layer approaches an impermeable wall. We also performed energy budget analysis to provide a physical interpretation for the behavior of the flow. We found that the energy production due to the Reynolds stress causes the disturbances to grow which consequently triggers the instability.

Appendix A

In order to check the convergence of spectrum obtained from the numerical experiment, the relative error is defined as mentioned in Tilton and Cortelezzi [10].

$$\begin{aligned} e_{N}=\, \frac{\left\| c_{N+1}-c_{N} \right\| _{2}}{\left\| c_{N} \right\| _{2}}, \end{aligned}$$

(A.1)

where $\left\| \bullet \right\|$ represent the $L_{2}$ norm. $c_{N+1}$ and $c_{N}$ are vectors whose components are the least twenty stable eigenvalues calculated using $N+1$ and N, respectively, in each region. Figure 14 illustrates the variation of error function with respect to the number of collocation points N. It can be seen that for both cases $U^{*} = 0$ & 1, roughly 75 Chebyshev polynomials is required to attain an error on the order of ${10}^{-6}$. Hence, we performed our calculations using 75 Chebyshev polynomials.

Fig. 14

Log–log plot of the variation of the relative error, $e_{N}$, with the number of Chebyshev polynomials, N, employed to solve the eigenvalue problem for the case $k =$ 1, $\mathrm{{Re}} = 1000$, $\alpha = 75$, $\delta = 1$, $\varepsilon = 0.6$, (a) $U^{*} = 0$, and (b) $U^{*} = 1$