Effective diffusivity for a mixed-matrix membrane

Abstract

The effective diffusivity or permeability of a mixed-matrix membrane composed of spherical fillers of one material distributed within a continuous matrix of another material is computed by a boundary-element method. The boundary value of the concentration of the diffusing species on the surface of the fillers is proportional to that of the adjoining matrix phase according to a linear sorption/desorption kinetics law that is responsible for an interfacial partition coefficient, while the diffusive flux is continuous across the interface. The solution of Laplace’s equation for the concentration field is constructed in terms of the single- and double-layer harmonic potentials involving the boundary values and boundary distribution of the normal derivative of the concentration and the free-space Green’s function of Laplace’s equation in three dimensions according to the standard boundary-integral formulation. The effective permeability of the membrane depends on the ratio of the filler-to-matrix permeabilities and not separately on the diffusivity ratio and partition coefficient. The results are in excellent agreement with the predictions of existing analytical models for random and ordered distributions of spherical particles within an infinite, continuous medium in the entire range of filler volume fractions considered. Extensions to systems governed by an interfacial contact resistance and nonlinear interfacial kinetics are discussed.

Appendices

Appendix A: Effective diffusivity at small volume fractions

For a given arrangement of filler particles, asymptotic and approximate methods provide predictions for the effective diffusivity or permeability of a mixed-matrix membrane containing spherical particles at small filler volume fractions as a function of two parameters,

$$\begin{aligned} \frac{D_{\mathrm{eff}}}{D_m} = f(k \alpha , c_v), \end{aligned}$$

(A.1)

where k is the partition coefficient at the matrix–filler interface, $\alpha \equiv D_f/D_m$ is the ratio of the diffusivity of the spherical fillers to that of the matrix, and $c_v$ is the volume fraction of the filler.

The simplest model is an adaptation of Maxwell’s seminal result [1] in electrostatics, yielding

$$\begin{aligned} f(k \alpha , c_v) \simeq \frac{k \alpha + 2 + 2 c_v (k \alpha -1)}{k \alpha + 2 - c_v (k \alpha -1)} + O(c_v^2) = 1 + 3 \, \frac{k \alpha - 1}{k \alpha + 2} \, c_v + O(c_v^2). \end{aligned}$$

(A.2)

In Maxwell’s asymptotic analysis, the scalar distribution in and around an isolated sphere suspended in an infinite matrix subject to a uniform gradient far from the sphere is employed to compute the effective diffusivity of a dilute dispersion, with the presence of other spheres neglected. Although the framework is limited formally to very small volume fractions, Maxwell’s predictions based on the first form of the expression in (A.2) have been shown to be reasonably accurate even for moderate volume fractions of fillers. The $O(c_v^2)$ contribution resulting from sphere–sphere interactions in random suspensions for $c_v \ll 1$ was given by Jeffrey [25].

Maxwell’s analysis was extended by Rayleigh [23] to nondilute systems of spherical particles arranged in a simple cubic lattice to yield an infinite series for the effective diffusivity ratio. Meredith and Tobias [26] reformulate the results as a truncated series,

$$\begin{aligned} f(k\alpha , c_v) = 1 + \frac{3}{\Lambda } \, c_v, \end{aligned}$$

(A.3)

where

$$\begin{aligned} \Lambda = \frac{k \alpha + 2}{k \alpha -1}&- c_v - 1.315 \, \frac{c_v^{10/3}}{(k \alpha + 4/3)/(k \alpha -1) - 0.409 c_v^{7/3}} - 0.016 \frac{(k \alpha - 1) c_v^{14/3}}{k \alpha + 6/5} . \end{aligned}$$

(A.4)

Corresponding result for a face-centered cubic lattice of spherical particles was derived by de Vries [24] to a lower order in $c_v$,

$$\begin{aligned} \Lambda = \frac{k \alpha + 2}{k \alpha -1} - c_v - 0.0752 \, \frac{(k \alpha - 1) c_v^{10/3}}{k \alpha + 4/3} . \end{aligned}$$

(A.5)

For a body-centered cubic lattice, the coefficient 0.0752 is replaced by 0.129 [24].

More complicated models result in implicit expressions for the effective diffusivity and include additional parameters such as the particle shape or size distribution of polydisperse fillers. For example, the Lewis–Nielsen model [27] has been shown to describe a vast amount of available experimental data on the thermal and electrical conductivities of particulate composites [28]. It predicts an effective diffusivity

$$\begin{aligned} \frac{D_\mathrm {eff}}{D_m} = \frac{1+A B c_v }{1 - B F c_v}, \end{aligned}$$

(A.6)

where

$$\begin{aligned} A = k_E - 1, \qquad B = \frac{k \alpha -1}{k \alpha + 2}, \qquad F = 1 + \left( \frac{1 - c_{v, \mathrm{max}}}{c_{v, \mathrm{max}}^2} \right) c_v, \end{aligned}$$

(A.7)

$k_E$ is the Einstein coefficient, equal to 5/2 for rigid spheres, and $c_{v, \mathrm{max}}$ is the maximum packing volume fraction of particles: $c_{v, \mathrm{max}} = 0.637$ for spheres in random close packing, $\pi /6$ for a simple cubic lattice, and $\pi /(3 \sqrt{2})$ for a fcc lattice or hexagonal packing. It has been suggested that $A = 2.0$ (instead of 1.5) for spherical particles so that the Lewis–Nielsen model reduces to the Maxwell model as $c_{v, \mathrm{max}} \rightarrow 1$ [28]. As $k \alpha \rightarrow \infty$, the Lewis–Nielsen model predicts that $D_{\mathrm{eff}} / D_m \rightarrow \infty$ when $c_v \rightarrow c_{v, \mathrm{max}}$ because touching particles provide pathways with negligible resistance for diffusive transport through the membrane, corresponding to a percolation threshold. Other commonly employed models for composite materials are reviewed by Petropoulos [3].

Appendix B: Effective diffusivity of a dilute suspension of spheres with an interfacial contact resistance

Consider a sphere of radius a composed of filler material that is suspended in a matrix with a linear ambient concentration field of strength G, such that the solute concentration far from the sphere is

$$\begin{aligned} \psi ({\mathbf {x}}) = {\mathbf {x}}\cdot \varvec{}{G} \qquad \mathrm {as} \quad | {\mathbf {x}}| \rightarrow \infty , \end{aligned}$$

(B.1)

where $\varvec{}{G}$ is a specified gradient with $| \varvec{}{G} | = G$ and ${\mathbf {x}}$ is the position vector with respect to the center of the sphere. At the interface between the spherical filler and surrounding matrix, the required conditions are continuity of the diffusive flux according to (4) and a jump in the concentration determined by the contact resistance according to (39). These conditions are imposed at $| {\mathbf {x}}| = a$. The Laplace equation governing the concentration distribution outside and inside the sphere can be solved by constructing scalar functions that are linear in $\varvec{}{G}$ from vector harmonic functions and applying the above boundary conditions to determine the three unknown constants,

$$\begin{aligned} \psi ({\mathbf {x}}) = \left( 1 - \beta \frac{a^3}{| {\mathbf {x}}|^3} \right) \, {\mathbf {x}}\cdot \varvec{}{G}, \qquad \phi ({\mathbf {x}}) = \frac{1+2 \beta }{\alpha } \, {\mathbf {x}}\cdot \varvec{}{G}, \end{aligned}$$

(B.2)

where

$$\begin{aligned} \beta = \frac{k \alpha - (1+r_c)}{k \alpha + 2(1+r_c)}, \end{aligned}$$

(B.3)

k is the interfacial partition coefficient, $\alpha = D_f/D_m$ is the filler-to-matrix ratio of the diffusivity, and

$$\begin{aligned} r_c = \frac{D_{f}}{a k_c} = \frac{\alpha D_{m}}{a k_c } \end{aligned}$$

(B.4)

is a dimensionless contact resistance for mass transfer across the matrix–filler interface. The interfacial contact coefficient, $k_c$, is defined as the ratio of the interfacial molar flux, $J^*$, to the concentration difference across the interface according to

$$\begin{aligned} J^* = k_c ( k \psi - \phi ) = D_m {\mathbf {n}}^{(1)} \cdot \nabla \psi . \end{aligned}$$

(B.5)

Using Maxwell’s formulation, the scaled effective diffusivity of a dilute dispersion of spherical fillers is then given approximately by

$$\begin{aligned} \frac{D_{\mathrm{eff}}}{D_m} \simeq \frac{1 + 2 \beta c_v}{1 - \beta c_v}. \end{aligned}$$

(B.6)

In the limit of a vanishing contact resistance, $r_c \rightarrow 0$, (B.6) reduces to (A.2).

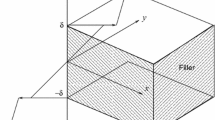
Appendix C: One-dimensional layer model for diffusion through a composite medium with nonlinear interfacial kinetics

Consider steady, one-dimensional diffusion through the matrix of a membrane confined between two planes located at $z = \pm \delta$. A filler layer is contained within the matrix and occupies the space $-a \le z \le a$, with $a < \delta$, as illustrated in Fig. 1. The solute concentration fields in the matrix, $\psi (z)$, and filler, $\phi (z)$, satisfy Laplace’s equation,

$$\begin{aligned} \frac{\mathrm{{d}}^2 \psi }{\mathrm{{d}} z^2} = 0, \qquad \frac{\mathrm{{d}}^2 \phi }{\mathrm{{d}}z^2}=0. \end{aligned}$$

(C.1)

The solute concentration is specified at the boundaries of the matrix,

$$\begin{aligned} \psi (-\delta ) = \psi _{-}, \qquad \psi (\delta ) = \psi _{+}. \end{aligned}$$

(C.2)

At the interface between the filler and matrix, there is a jump in the solute concentration according to (42),

$$\begin{aligned} \phi = k_F' \psi ^m \quad \mathrm {at} \quad z=\pm a, \end{aligned}$$

(C.3)

and continuity of the diffusive flux,

$$\begin{aligned} D_m \left. \frac{\mathrm{{d}} \psi }{\mathrm{{d}}z} \right| _{z=\pm a} = D_f \left. \frac{\mathrm{{d}} \phi }{\mathrm{{d}} z} \right| _{z=\pm a}. \end{aligned}$$

(C.4)

Using elementary methods, the solution of the boundary-value problem is found to be

$$\begin{aligned} \psi (z)= & {} \psi _{-} + \left[ \psi _+ - \psi (a) \right] \left( \frac{\delta +z}{\delta -a} \right) , \quad -\delta \le z \le -a, \nonumber \\ \phi (z)= & {} \frac{1}{2} \left[ \phi (a) + \phi (-a) \right] + \frac{z}{2a} \left[ \phi (a) - \phi (-a) \right] , \quad -a \le z \le a, \nonumber \\ \psi (z)= & {} \psi _+ - \left[ \psi _+ - \psi (a) \right] \left( \frac{\delta -z}{\delta -a} \right) , \qquad a \le z \le \delta , \end{aligned}$$

(C.5)

where $\psi (a)$ is the matrix-phase concentration at $z=a$ and is given implicitly by

$$\begin{aligned} \frac{(\delta - a) k_F' \alpha }{2a} \left[ \psi ^m(a) - \left( \psi _+ + \psi _{-} - \psi (a) \right) ^m \right] = \psi _+ - \psi (a). \end{aligned}$$

(C.6)

The interfacial filler-phase concentrations are

$$\begin{aligned} \phi (a) = k_F' \psi ^m(a), \qquad \phi (-a) = k_F' \left[ \psi _+ + \psi _{-} - \psi (a) \right] ^m, \end{aligned}$$

(C.7)

where $\alpha = D_f/D_m$.

Using Fick’s law, the diffusive flux across the layer is

$$\begin{aligned} J^* = -D_m \left. \frac{\mathrm{{d}} \psi }{\mathrm{{d}} z} \right| _{z=\delta } = \frac{D_m}{\delta -a} \left[ \psi (a) - \psi _+ \right] . \end{aligned}$$

(C.8)

An effective diffusivity of the composite system can be defined using the integrated form of Fick’s law,

$$\begin{aligned} J^* = -D_{\mathrm{eff}} \left( \frac{\psi _+ - \psi _{-}}{2 \delta } \right) . \end{aligned}$$

(C.9)

Using (C.8) and (C.9), the scaled effective diffusivity of the composite layer is

$$\begin{aligned} \frac{D_{\mathrm{eff}}}{D_m} = \frac{2 \delta }{\delta -a} \left[ \frac{ \psi (a)-\psi _{+}}{\psi _{-} - \psi _+} \right] . \end{aligned}$$

(C.10)

Without loss of generality, the parameter values are chosen to be $2 \delta =1$, $\psi _{-}=1$, and $\psi _+=0$, which gives

$$\begin{aligned} \frac{D_{\mathrm{eff}}}{D_m} = \frac{2 \psi (a)}{1-2a}. \end{aligned}$$

(C.11)

With the other parameters fixed, the scaled effective diffusivity is nonmonotonic in m and is maximized for

$$\begin{aligned} m = m^* \equiv \frac{\ln \left[ \ln \left( 1 - \psi (a) \right) / \ln \left( \psi (a) \right) \right] }{\ln \left[ \psi (a) / \left( 1 - \psi (a) \right) \right] }. \end{aligned}$$

(C.12)

As shown in Fig. 10, $m^* \approx \sqrt{2}$ for most values of $\psi (a)$, which must be computed from (C.6).

Using (C.6) and (C.11), the scaled effective diffusivity is seen to be identical for $m=1$ and $m=2$ for this one-dimensional layer model with the aforementioned choices of $\psi _+$ and $\psi _{-}$,

$$\begin{aligned} \frac{D_{\mathrm{eff}}}{D_m} = \frac{\delta k_F' \alpha }{(\delta -a) k_F' \alpha +a } \quad \mathrm {if} \quad m=1 ~ \mathrm {or} ~ 2. \end{aligned}$$

(C.13)

The volume fraction of filler for this layer model is $c_v = a/\delta$.