Negative Refraction of Mixing Waves in Nonlinear Elastic Wave Metamaterials

Abstract

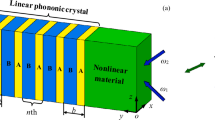
Nonlinear effects can enrich the propagation of elastic waves in mechanical metamaterials, which makes it possible to extend classical phenomena and functions in linear systems to nonlinear ones. In this work, rather than monochromatic waves in similar linear structures, the negative refraction is realized by mixing waves which are generated in nonlinear elastic wave metamaterials. Based on the stiffness matrix and plane wave expansion methods, dispersion curves of in–plane modes resulting from the collinear and non–linear mixings of two longitudinal waves are calculated. In the frequency spectrum, two propagating modes coalesce at exceptional points due to the coupling of in–plane modes, and those points at which the refraction type changes are also exceptional ones. Two kinds of negative refraction can be found in the mixing modes near exceptional points, but each of them needs to be induced in a specific configuration. Moreover, experiments are performed to support the pure negative refraction and beam splitting of the nonlinear elastic waves. Particularly, the parallel configuration is able to separate and extract the nonlinear mode when the single–mode negative refraction occurs, which shows the possibility to design elastic wave device by the negative refraction of nonlinear mixing waves.

Appendices

Appendix A

The elements of $\mathbf{{K}}_{m}^{j}$ in Eq. (27a), (27b) are

$$\begin{aligned} K_{m}^{j}(1,1) &= - K_{m}^{j}(2,2) = K_{m}^{j}(3,3) = - K_{m}^{j}(4,4) \\ &= \mathrm{i}\frac{\mu _{j}\kappa _{m}}{K_{0m}}\left \{ \left [ \kappa _{m}^{4} + \nu _{Tmj}^{2}\left ( 2\nu _{Lmj}^{2} - \kappa _{m}^{2} \right ) \right ]D_{Lmj}^{ -} D_{Tmj}^{ -} \right . \\ &\quad {} \left . + \left ( 3\kappa _{m}^{2} - \nu _{Tmj}^{2} \right )\nu _{Lmj}\nu _{Tmj}\left ( D_{Lmj}^{ +} D_{Tmj}^{ +} - 4\chi _{Lmj}\chi _{Tmj} \right ) \right \}, \end{aligned}$$

(A.1)

$$ K_{m}^{j}(1,2) = - K_{m}^{j}(3,4) = - \mathrm{i}\frac{\mu _{j}\nu _{Lmj}k_{Tmj}^{2}}{K_{0m}}\left ( \nu _{Lmj}\nu _{Tmj}D_{Lmj}^{ -} D_{Tmj}^{ +} + \kappa _{m}^{2}D_{Lmj}^{ +} D_{Tmj}^{ -} \right ), $$

(A.2)

$$\begin{aligned} K_{m}^{j}(1,3) &= K_{m}^{j}(2,4) = K_{m}^{j}(3,1) = K_{m}^{j}(4,2) \\ &= 2\mathrm{i}\frac{\mu _{j}\nu _{Lmj}\nu _{Tmj}\kappa _{m}k_{Tmj}^{2}}{K_{0m}}\left ( \chi _{Lmj}D_{Tmj}^{ +} - \chi _{Tmj}D_{Lmj}^{ +} \right ), \end{aligned}$$

(A.3)

$$ K_{m}^{j}(1,4) = - K_{m}^{j}(3,2) = 2\mathrm{i}\frac{\mu _{j}\nu _{Lmj}k_{Tmj}^{2}}{K_{0m}}\left ( \nu _{Lmj}\nu _{Tmj}\chi _{Tmj}D_{Lmj}^{ -} + \kappa _{m}^{2}\chi _{Lmj}D_{Tmj}^{ -} \right ), $$

(A.4)

$$ K_{m}^{j}(2,1) = - K_{m}^{j}(4,3) = - \mathrm{i}\frac{\mu _{j}\nu _{Tmj}k_{Tmj}^{2}}{K_{0m}}\left ( \nu _{Lmj}\nu _{Tmj}D_{Lmj}^{ +} D_{Tmj}^{ -} + \kappa _{m}^{2}D_{Lmj}^{ -} D_{Tmj}^{ +} \right ), $$

(A.5)

$$ K_{m}^{j}(2,3) = - K_{m}^{j}(4,1) = 2\mathrm{i}\frac{\mu _{j}\nu _{Tmj}k_{Tmj}^{2}}{K_{0m}}\left ( \nu _{Lmj}\nu _{Tmj}\chi _{Lmj}D_{Tmj}^{ -} + \kappa _{m}^{2}\chi _{Tmj}D_{Lmj}^{ -} \right ), $$

(A.6)

where $D_{Qmj}^{ \pm} = \chi _{Qmj}^{2} \pm 1$, $\chi _{Qmj} = \exp \left ( \mathrm{i}\nu _{Qmj}h_{j} \right )$ and

$$ K_{0mj} = \left ( \kappa _{m}^{4} + \nu _{Lmj}^{2}\nu _{Tmj}^{2} \right )D_{Lmj}^{ -} D_{Tmj}^{ -} + 2\nu _{Lmj}\nu _{Tmj}\kappa _{m}^{2}\left ( D_{Lmj}^{ +} D_{Tmj}^{ +} - 4\chi _{Lmj}\chi _{Tmj} \right ). $$

(A.7)

Appendix B

The coefficients $\varepsilon _{ym}$ in Eq. (32) are

$$ \varepsilon _{0m} = \varepsilon _{4m} = |\mathbf{K}_{12m}^{n}|, $$

(B.1)

$$\begin{aligned} \varepsilon _{1m} &= \varepsilon _{3m} \\ &= \mathbf{K}_{m}^{n}(1,1)\mathbf{K}_{m}^{n}(2,4) - \mathbf{K}_{m}^{n}(1,2)\mathbf{K}_{m}^{n}(2,3) + \mathbf{K}_{m}^{n}(1,3)\left [ \mathbf{K}_{m}^{n}(2,2) - \mathbf{K}_{m}^{n}(4,4) \right ] \\ &\quad {} - \mathbf{K}_{m}^{n}(1,4)\left [ \mathbf{K}_{m}^{n}(2,1) - \mathbf{K}_{m}^{n}(4,3) \right ] + \mathbf{K}_{m}^{n}(2,3)\mathbf{K}_{m}^{n}(3,4) - \mathbf{K}_{m}^{n}(2,4)\mathbf{K}_{m}^{n}(3,3), \end{aligned}$$

(B.2)

$$\begin{aligned} \varepsilon _{2m} &= |\mathbf{K}_{11m}^{n}| + |\mathbf{K}_{22m}^{n}| - \mathbf{K}_{m}^{n}(1,1)\mathbf{K}_{m}^{n}(4,4) + \mathbf{K}_{m}^{n}(1,2)\mathbf{K}_{m}^{n}(4,3) \\ &\quad {}- \mathbf{K}_{m}^{n}(1,3)\mathbf{K}_{m}^{n}(4,2) + \mathbf{K}_{m}^{n}(1,4)\mathbf{K}_{m}^{n}(4,1) + \mathbf{K}_{m}^{n}(2,1)\mathbf{K}_{m}^{n}(3,4) \\ &\quad {} - \mathbf{K}_{m}^{n}(2,2)\mathbf{K}_{m}^{n}(3,3) + \mathbf{K}_{m}^{n}(2,3)\mathbf{K}_{m}^{n}(3,2) - \mathbf{K}_{m}^{n}(2,4)\mathbf{K}_{m}^{n}(3,1). \end{aligned}$$

(B.3)

Appendix C

The expressions of matrices $\mathbf{X}_{zm}$ and $\mathbf{Y}_{zm}$ in Eq. (36a), (36b) are

$$ \mathbf{X}_{0m} = \left [ \textstyle\begin{array}{c@{\quad}c} G'G''\left [ \lambda \left ( G \right ) + 2\mu \left ( G \right ) \right ] + \mu \left ( G \right )\kappa _{m}^{2} & \left [ G'\mu \left ( G \right ) + G''\lambda \left ( G \right ) \right ]\kappa _{m} \\ \left [ G'\lambda \left ( G \right ) + G''\mu \left ( G \right ) \right ]\kappa _{m} & G'G''\mu \left ( G \right ) + \left [ \lambda \left ( G \right ) + 2\mu \left ( G \right ) \right ]\kappa _{m}^{2} \end{array}\displaystyle \right ], $$

(C.1)

$$ \mathbf{X}_{1m} = \left [ \textstyle\begin{array}{c@{\quad}c} \left ( G' + G'' \right )\left [ \lambda \left ( G \right ) + 2\mu \left ( G \right ) \right ] & \left [ \lambda \left ( G \right ) + \mu \left ( G \right ) \right ]\kappa _{m} \\ \left [ \lambda \left ( G \right ) + \mu \left ( G \right ) \right ]\kappa _{m} & \left ( G' + G'' \right ) \cdot \mu \left ( G \right ) \end{array}\displaystyle \right ], $$

(C.2)

$$ \mathbf{X}_{2m} = \left [ \textstyle\begin{array}{c@{\quad}c} \lambda \left ( G \right ) + 2\mu \left ( G \right ) & 0 \\ 0 & \mu \left ( G \right ) \end{array}\displaystyle \right ], $$

(C.3)

$$ \mathbf{Y}_{0m} = \left [ \textstyle\begin{array}{c@{\quad}c} \left ( G'' + k_{m}^{B} \right )\left ( G' + k_{m}^{B} \right )\left [ \lambda \left ( G \right ) + 2\mu \left ( G \right ) \right ] & 0 \\ 0 & \left ( G'' + k_{m}^{B} \right )\left ( G' + k_{m}^{B} \right )\mu \left ( G \right ) \end{array}\displaystyle \right ]. $$

(C.4)

$$ \mathbf{Y}_{1m} = \left [ \textstyle\begin{array}{c@{\quad}c} 0 & \left ( G'' + k_{m}^{B} \right )\lambda \left ( G \right ) + \left ( G' + k_{m}^{B} \right )\mu \left ( G \right ) \\ \left ( G'' + k_{m}^{B} \right )\mu \left ( G \right ) + \left ( G' + k_{m}^{B} \right )\lambda \left ( G \right ) & 0 \end{array}\displaystyle \right ], $$

(C.5)

$$ \mathbf{Y}_{2m} = \left [ \textstyle\begin{array}{c@{\quad}c} \mu \left ( G \right ) & 0 \\ 0 & \lambda \left ( G \right ) + 2\mu \left ( G \right ) \end{array}\displaystyle \right ], $$

(C.6)