Nonreciprocal Transmission of Non-collinear Mixing Wave in Nonlinear Elastic Wave Metamaterial

Abstract

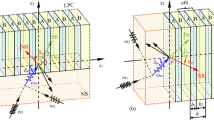
This investigation is focused on the nonreciprocal transmission of the non-collinear mixing wave in a nonlinear elastic wave metamaterial. The nonlinear elastic wave metamaterial with asymmetric structure is used to break the traditional reciprocal transmission, which is composed of a nonlinear material and a linear phononic crystal. When two non-collinear shear waves following the resonant condition interact with each other, the sum frequency longitudinal wave can be generated and propagate together with fundamental and second harmonics. Based on the transfer and stiffness matrices, band gaps and transmission coefficients are derived. The changing of band structures results in manipulating elastic waves with different frequencies. In the nonreciprocal frequency region, elastic waves can propagate along the positive direction while the reverse case is prohibited. The mixing of two incident SV waves in the nonlinear elastic wave metamaterial is verified by experiments and the results can support the theoretical analysis and numerical calculations. Because of material nonlinearity and asymmetric structure, the nonlinear elastic wave metamaterial can behave as a mechanical diode. The present work shows the possibility to design nonreciprocal elastic wave device by nonlinear wave mixing methods.

Appendices

Appendix A

The displacement of the SH wave in the periodic structure is

$$\begin{aligned} \mathbf{u}_{rj}^{(1)} &= \left \{ U_{rj}\hat{\mathbf{x}}\exp \left [ \mathrm{i}\omega _{r}\beta _{Trj}\left ( y - y_{n - 1} \right ) / c_{r} \right ] + R_{rj}\hat{\mathbf{x}}\exp \left [ \mathrm{i}\omega _{r}\beta _{Trj}\left ( y_{n} - y \right ) / c_{r} \right ] \right \} \\ &\quad {}\times\exp \left [ \mathrm{i}\omega _{r}\left ( z / c_{r} - t \right ) \right ], \end{aligned}$$

(25)

where $U_{rj}$ and $R_{rj}$ are amplitudes of incident and reflected SH waves.

Moreover, the stress component can be derived as

$$ \tau _{yzrj}^{(1)} = \mu _{j}\frac{\partial u_{rj}^{(1)}}{\partial y}. $$

(26)

Substituting Eq. (25) into Eq. (26), we can obtain that

$$\begin{aligned} \tau _{yzrj}^{(1)} &= \frac{\mathrm{i}\mu _{j}\omega _{r}\beta _{Trj}}{c_{r}}\left \{ U_{rj}\exp \left [ \mathrm{i}\omega _{r}\beta _{Trj}\left ( y - y_{n - 1} \right ) / c_{r} \right ] \right . \\ &\quad \left . + R_{rj}\exp \left [ \mathrm{i}\omega _{r}\beta _{Trj}\left ( y_{n} - y \right ) / c_{r} \right ] \right \}\exp \left [ \mathrm{i}\omega _{r}\left ( z / c_{r} - t \right ) \right ]. \end{aligned}$$

(27)

The displacement and stress of the SH wave on both sides of each sub cell can be written as

$$ \left \{ u_{r\mathrm{A}}^{(1)}, \tau _{yzr\mathrm{A}}^{(1)} \right \}_{y = y_{n}}^{\mathrm{T}} = \mathbf{T}_{r\mathrm{A}}\left \{ u_{r\mathrm{A}}^{(1)}, \tau _{yzr\mathrm{A}}^{(1)} \right \}_{y = y_{n - 1}}^{\mathrm{T}}, $$

(28a)

$$ \left \{ u_{r\mathrm{B}}^{(1)}, \tau _{yzr\mathrm{B}}^{(1)} \right \}_{y = y_{n + 1}}^{\mathrm{T}} = \mathbf{T}_{r\mathrm{B}}\left \{ u_{r\mathrm{B}}^{(1)}, \tau _{yzr\mathrm{B}}^{(1)} \right \}_{y = y_{n}}^{\mathrm{T}}, $$

(28b)

where $\mathbf{T}_{rj}$ refers to the transfer matrix of sub cell A or B with the parameter $\chi _{\mathit{Trj}} = \exp(\text{i}\omega _{r}\beta _{\mathit{Trj}} b_{j}/c_{r})$ as

$$ \mathbf{T}_{rj} = \frac{1}{2}\left [ \textstyle\begin{array}{c@{\quad}c} \chi _{Trj} + \chi _{Trj}^{ - 1} & \frac{\left ( \chi _{Trj} - \chi _{Trj}^{ - 1} \right )c_{r}}{\mathrm{i}\mu _{j}\omega _{r}\beta _{Trj}} \\ \mathrm{i}\mu _{j}\omega _{r}\beta _{Trj}(\chi _{Trj} - \chi _{Trj}^{ - 1}) / c_{r} & \chi _{Trj} + \chi _{Trj}^{ - 1} \end{array}\displaystyle \right ]. $$

(29)

It can be obtained from Eqs. (28a) and (28b) that displacements and stresses on both sides of a unit cell are

$$ \left \{ u_{r\mathrm{B}}^{(1)}, \tau _{yzr\mathrm{B}}^{(1)} \right \}_{y = y_{n + 1}}^{\mathrm{T}} = \mathbf{T}_{r}\left \{ u_{r\mathrm{A}}^{(1)}, \tau _{yzr\mathrm{A}}^{(1)} \right \}_{y = y_{n - 1}}^{\mathrm{T}}, $$

(30)

where $\mathbf{T}_{r} = \mathbf{T}$_rB$\mathbf{T}$_rA.

Based on the Bloch theory, the eigenvalue equation is derived and the dispersion relation of SH wave can be obtained. Moreover, the stresses on both sides of each sub cell can be expressed as

$$ \left \{ \tau _{yzr\mathrm{A}}^{(1)}|_{y = y_{n - 1}}, \tau _{yzr\mathrm{A}}^{(1)}|_{y = y_{n}} \right \}^{\mathrm{T}} = \mathbf{K}_{r\mathrm{A}}\left \{ u_{r\mathrm{A}}^{(1)}|_{y = y_{n - 1}}, u_{r\mathrm{A}}^{(1)}|_{y = y_{n}} \right \}^{\mathrm{T}}, $$

(31a)

$$ \left \{ \tau _{yzr\mathrm{B}}^{(1)}|_{y = y_{n}}, \tau _{yzr\mathrm{B}}^{(1)}|_{y = y_{n + 1}} \right \}^{\mathrm{T}} = \mathbf{K}_{r\mathrm{B}}\left \{ u_{r\mathrm{B}}^{(1)}|_{y = y_{n}}, u_{r\mathrm{B}}^{(1)}|_{y = y_{n + 1}} \right \}^{\mathrm{T}}, $$

(31b)

where $\mathbf{K}_{rj}$ refers to the stiffness matrix of the sub cell A or B, and its elements are

$$ K_{rj11} = - K_{rj22} = \frac{\mathrm{i}\mu _{j}\omega _{r}\beta _{Trj}\left ( 1 + \chi _{Trj}^{2} \right )}{\left ( 1 - \chi _{Trj}^{2} \right )c_{r}},\quad K_{rj12} = - K_{rj21} = - \frac{2\mathrm{i}\mu _{j}\omega _{r}\beta _{Trj}\chi _{Trj}}{\left ( 1 - \chi _{Trj}^{2} \right )c_{r}}. $$

(32a, b)

Similarly, stresses and displacements on both sides of the $n$th unit cell can be expressed as

$$ \left \{ \tau _{yzr\mathrm{B}}^{(1)}|_{y = y_{n - 1}}, \tau _{yzr\mathrm{B}}^{(1)}|_{y = y_{n + 1}} \right \}^{\mathrm{T}} = \mathbf{K}_{r}^{n}\left \{ u_{r\mathrm{B}}^{(1)}|_{y = y_{n - 1}}, u_{r\mathrm{B}}^{(1)}|_{y = y_{n + 1}} \right \}^{\mathrm{T}}, $$

(33)

where $\mathbf{K}_{r}^{n}$ is the stiffness matrix of the $n$th unit cell.

According to Eqs. (31a)–(33), we can derive the expressions of $\mathbf{K}_{r}^{n}$ as

$$ \mathbf{K}_{r}^{n} = \left [ \textstyle\begin{array}{c@{\quad}c} K_{r\mathrm{A}11} - K_{r\mathrm{A}12}K_{rn}K_{r\mathrm{A}21} & K_{r\mathrm{A}12}K_{rn}K_{r\mathrm{B}12} \\ - K_{r\mathrm{B}21}K_{rn}K_{r\mathrm{A}21} & K_{r\mathrm{B}22} + K_{r\mathrm{B}21}K_{rn}K_{r\mathrm{B}12} \end{array}\displaystyle \right ], $$

(34)

where $K_{rn} = (K_{r\mathrm{A}22} - K_{r\mathrm{B}11})^{ - 1}$.

Following the previous procedure and repeating the above derivation, the global stiffness matrix is

$$ \mathbf{K}_{r}^{N} = \left [ \textstyle\begin{array}{c@{\quad}c} K_{r11}^{N - 1} - K_{r12}^{N - 1}K_{rN}K_{r21}^{N - 1} & K_{r12}^{N - 1}K_{rN}K_{r12}^{n} \\ - K_{r21}^{n}K_{rN}K_{r21}^{N - 1} & K_{r22}^{n} + K_{r21}^{n}K_{rN}K_{r12}^{n} \end{array}\displaystyle \right ], $$

(35)

where $\mathbf{K}_{r}^{N - 1}$ is the stiffness matrix for $n - 1$ unit cells and $K_{rN} = (K_{r22}^{N - 1} - K_{r11}^{n})^{ - 1}$.

Then, equations describing the stress and displacement of SH wave can be established through the global stiffness matrix. With the superscripts R and L denoting the boundary conditions on the right and left sides of the phononic crystal, we can derive that

$$ \left \{ \tau _{yzr\mathrm{R}}, \tau _{yzr\mathrm{L}} \right \}^{\mathrm{T}} = \mathbf{K}_{r}^{N}\left \{ u_{r\mathrm{R}}, u_{r\mathrm{L}} \right \}^{\mathrm{T}}, $$

(36)

where $u$_rR = $U_{r} + R_{r}$, $u$_rL = $T_{r}$, $U_{r}$, $R_{r}$, and $T_{r}$ are amplitudes of the incident, reflected and transmitted SH waves, and $\tau$_yzrR and $\tau$_yzrL are stresses.

Based on Eq. (36), the transmission coefficient of fundamental SH wave is

$$\begin{aligned} &\mathrm{TF}_{\mathrm{SH}r} \\ &= \frac{ - 2\mathrm{i}\mu _{\mathrm{A}}\omega _{r}c_{r}\beta _{Tr\mathrm{A}}K_{r21}^{N}}{\mu _{\mathrm{A}}\mu _{\mathrm{B}}\omega _{r}^{2}\beta _{Tr\mathrm{A}}\beta _{Tr\mathrm{B}} + \left ( K_{r11}^{N}K_{r22}^{N} - K_{r12}^{N}K_{r21}^{N} \right )c_{r}^{2} + \mathrm{i}\omega _{r}c_{r}\left ( \mu _{\mathrm{A}}\beta _{Tr\mathrm{A}}K_{r22}^{N} - \mu _{\mathrm{B}}\beta _{Tr\mathrm{B}}K_{r11}^{N} \right )}. \end{aligned}$$

(37)

Appendix B

The elements of transfer matrix $\mathbf{T}_{sj}$ in Eqs. (14a), (14b) are

$$ T_{sj11} = \frac{1}{p_{sj}}\left [ \frac{q_{sj}}{2}\left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ], $$

(38)

$$ T_{sj12} = \frac{1}{h_{sj}}\left [ \mu _{j}\beta _{Lsj}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) - \frac{g_{sj}}{2\beta _{Tsj}}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(39)

$$ T_{sj13} = \frac{\mathrm{i}c_{s}}{2\mu _{j}\omega _{s}p_{sj}}\left [ - \left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ], $$

(40)

$$ T_{sj14} = - \frac{\mathrm{i}c_{s}}{2\omega _{s}h_{sj}}\left [ \beta _{Lsj}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) + \frac{1}{\beta _{Tsj}}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(41)

$$ T_{sj21} = \frac{1}{p_{sj}}\left [ \frac{q_{sj}}{2\beta _{Lsj}}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) - \beta _{Tsj}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(42)

$$ T_{sj22} = \frac{1}{h_{sj}}\left [ \mu _{j}\left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + \frac{g_{sj}}{2}\left ( \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ) \right ], $$

(43)

$$ T_{sj23} = - \frac{\mathrm{i}c_{s}}{2\mu _{j}\omega _{s}p_{sj}}\left [ \frac{1}{\beta _{Lsj}}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) + \beta _{Tsj}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(44)

$$ T_{sj24} = \frac{\mathrm{i}c_{s}}{2\omega _{s}h_{sj}}\left [ - \left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ], $$

(45)

$$ T_{sj31} = \frac{\mathrm{i}\mu _{j}\omega _{s}q_{sj}}{c_{s}p_{sj}}\left [ \chi _{Lsj} + \chi _{Lsj}^{ - 1} - \left ( \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ) \right ], $$

(46)

$$ T_{sj32} = \frac{\mathrm{i}\mu _{j}\omega _{s}}{c_{s}h_{sj}}\left [ 2\mu _{j}\beta _{Lsj}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) + \frac{g_{sj}q_{sj}}{2\beta _{Tsj}}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(47)

$$ T_{sj33} = \frac{1}{2p_{sj}}\left [ 2\left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + q_{sj}\left ( \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ) \right ], $$

(48)

$$ T_{sj34} = \frac{\mu _{j}}{2h_{sj}}\left [ 2\beta _{Lsj}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) - \frac{q_{sj}}{\beta _{Tsj}}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(49)

$$ T_{sj41} = \frac{\mathrm{i}\omega _{s}}{c_{s}p_{sj}}\left [ \frac{g_{sj}q_{sj}}{2\beta _{Lsj}}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) + 2\mu _{j}\beta _{Tsj}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(50)

$$ T_{sj42} = \frac{\mathrm{i}\mu _{j}\omega _{s}g_{sj}}{c_{s}h_{sj}}\left [ \chi _{Lsj} + \chi _{Lsj}^{ - 1} - \left ( \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ) \right ], $$

(51)

$$ T_{sj43} = \frac{1}{2\mu _{j}p_{sj}}\left [ \frac{g_{sj}}{\beta _{Lsj}}\left ( \chi _{Lsj} - \chi _{Lsj}^{ - 1} \right ) - 2\mu _{j}\beta _{Tsj}\left ( \chi _{Tsj} - \chi _{Tsj}^{ - 1} \right ) \right ], $$

(52)

$$ T_{sj44} = \frac{1}{2h_{sj}}\left [ g_{sj}\left ( \chi _{Lsj} + \chi _{Lsj}^{ - 1} \right ) + 2\mu _{j}\left ( \chi _{Tsj} + \chi _{Tsj}^{ - 1} \right ) \right ], $$

(53)

where $g_{sj} = \varepsilon _{j}\beta _{Lsj}^{2} + \lambda _{j}$, $h_{sj} = \varepsilon _{j}(\beta _{Lsj}^{2} + 1)$, $p_{sj} = \beta _{Tsj}^{2} + 1$, $q_{sj} = \beta _{Tsj}^{2} - 1$ and $\chi _{Qsj} = \exp (\mathrm{i}\omega _{s}\beta _{Qsj}b_{j}/c_{s})$.

Appendix C

The elements of stiffness matrix $\mathbf{K}_{sj}$ in Eqs. (16a), (16b) are

$$ K_{sj11} = u_{j}\kappa _{sj}\left [ 2K_{j0} - p_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\xi _{sj}^{ +} \eta _{sj}^{ +} + \xi _{sj}^{ -} \eta _{sj}^{ -} - 4\beta _{Lsj}\beta _{Tsj}\chi _{Lsj}\chi _{Tsj} \right ) \right ], $$

(54)

$$ K_{sj12} = - u_{j}\kappa _{sj}\beta _{Lsj}p_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\xi _{sj}^{ -} \eta _{sj}^{ +} + \xi _{sj}^{ +} \eta _{sj}^{ -} \right ), $$

(55)

$$ K_{sj13} = 2u_{j}\kappa _{sj}\beta _{Lsj}\beta _{Tsj}p_{sj}\left ( \chi _{Lsj}\eta _{sj}^{ +} - \chi _{Tsj}\xi _{sj}^{ +} \right ), $$

(56)

$$ K_{sj14} = 2u_{j}\kappa _{sj}\beta _{Lsj}p_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\chi _{Tsj}\xi _{sj}^{ -} + \chi _{Lsj}\eta _{sj}^{ -} \right ), $$

(57)

$$ K_{sj21} = - \kappa _{sj}\beta _{Tsj}h_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\xi _{sj}^{ +} \eta _{sj}^{ -} + \xi _{sj}^{ -} \eta _{sj}^{ +} \right ), $$

(58)

$$ K_{sj22} = \kappa _{sj}\left [ - 2\mu _{j}K_{j0} + h_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\xi _{sj}^{ +} \eta _{sj}^{ +} + \xi _{sj}^{ -} \eta _{sj}^{ -} - 4\beta _{Lsj}\beta _{Tsj}\chi _{Lsj}\chi _{Tsj} \right ) \right ], $$

(59)

$$ K_{sj23} = 2\kappa _{sj}\beta _{Tsj}h_{sj}\left ( \beta _{Lsj}\beta _{Tsj}\chi _{Lsj}\eta _{sj}^{ -} + \chi _{Tsj}\xi _{sj}^{ -} \right ), $$

(60)

$$ K_{sj24} = 2\kappa _{sj}\beta _{Lsj}\beta _{Tsj}h_{sj}\left ( \chi _{Lsj}\eta _{sj}^{ +} - \chi _{Tsj}\xi _{sj}^{ +} \right ), $$

(61)

$$ K_{sj31} = K_{sj13},\qquad K_{sj32} = - K_{sj14},\qquad K_{sj33} = K_{sj11},\qquad K_{sj34} = - K_{sj12}, $$

(62–65)

$$ K_{sj41} = - K_{sj23},\qquad K_{sj42} = K_{sj24},\qquad K_{sj43} = - K_{sj21},\qquad K_{sj44} = K_{sj22}, $$

(66–69)

where $\kappa _{sj} = \mathrm{i}\omega _{s} / (c_{s} K$_j0), $K_{0j} = (\beta _{Lsj}^{2}\beta _{Lsj}^{2} + 1)\xi _{sj}^{ -} \eta _{sj}^{ -} + 2\beta _{Lsj}\beta _{Tsj}(\xi _{sj}^{ +} \eta _{sj}^{ +} - 4\chi _{Lsj}\chi _{Tsj})$, $\xi _{sj}^{ \pm} = \chi _{Lsj}^{2} \pm 1$ and $\eta _{sj}^{ \pm} = \chi _{Tsj}^{2} \pm 1$.

Appendix D

The elements of matrix $\mathbf{D}_{s}$ in Eq. (21) are

$$ D_{s11} = \left [ \left ( - K_{s11}^{N} + 2\mathrm{i}\mu _{\mathrm{A}}\omega _{s} / c_{s} \right )\beta _{Ls\mathrm{A}} + K_{s12}^{N} \right ]\gamma _{Ls\mathrm{A}}, $$

(70)

$$ D_{s12} = - \left ( K_{s11}^{N} + K_{s12}^{N}\beta _{Ts\mathrm{A}} + \mathrm{i}\mu _{\mathrm{A}}\omega _{s}q_{s\mathrm{A}} / c_{s} \right )\gamma _{Ts\mathrm{A}}, $$

(71)

$$ D_{s13} = \left ( K_{s13}^{N}\beta _{Ls\mathrm{B}} + K_{s14}^{N} \right )\gamma _{Ls\mathrm{B}}, $$

(72)

$$ D_{s14} = \left ( - K_{s13}^{N} + K_{s14}^{N}\beta _{Ts\mathrm{B}} \right )\gamma _{Ts\mathrm{B}}, $$

(73)

$$ D_{s21} = - \left ( K_{s21}^{N}\beta _{Ls\mathrm{A}} - K_{s22}^{N} + \mathrm{i}\omega _{s}g_{s\mathrm{A}} / c_{s} \right )\gamma _{Ls\mathrm{A}}, $$

(74)

$$ D_{s22} = - \left [ K_{s21}^{N} + \left ( K_{s22}^{N} + 2\mathrm{i}\mu _{\mathrm{A}}\omega _{s} / c_{s} \right )\beta _{Ts\mathrm{A}} \right ]\gamma _{Ts\mathrm{A}}, $$

(75)

$$ D_{s23} = \left ( K_{s23}^{N}\beta _{Ls\mathrm{B}} + K_{s24}^{N} \right )\gamma _{Ls\mathrm{B}}, $$

(76)

$$ D_{s24} = \left ( - K_{s23}^{N} + K_{s24}^{N}\beta _{Ts\mathrm{B}} \right )\gamma _{Ts\mathrm{B}}, $$

(77)

$$ D_{s31} = \left ( - K_{s31}^{N}\beta _{Ls\mathrm{A}} + K_{s32}^{N} \right )\gamma _{Ls\mathrm{A}}, $$

(78)

$$ D_{s32} = - \left ( K_{s31}^{N} + K_{s32}^{N}\beta _{Ts\mathrm{A}} \right )\gamma _{Ts\mathrm{A}}, $$

(79)

$$ D_{s33} = \left [ \left ( K_{s33}^{N} - 2\mathrm{i}\mu _{\mathrm{B}}\omega _{s} / c_{s} \right )\beta _{Ls\mathrm{B}} + K_{s34}^{N} \right ]\gamma _{Ls\mathrm{B}}, $$

(80)

$$ D_{s34} = \left ( - K_{s33}^{N} + K_{s34}^{N}\beta _{Ts\mathrm{B}} - \mathrm{i}\mu _{\mathrm{B}}\omega _{s}q_{s\mathrm{B}} / c_{s} \right )\gamma _{Ts\mathrm{B}}, $$

(81)

$$ D_{s41} = \left ( - K_{s41}^{N}\beta _{Ls\mathrm{A}} + K_{s42}^{N} \right )\gamma _{Ls\mathrm{A}}, $$

(82)

$$ D_{s42} = - \left ( K_{s41}^{N} + K_{s42}^{N}\beta _{Ts\mathrm{A}} \right )\gamma _{Ts\mathrm{A}}, $$

(83)

$$ D_{s43} = \left ( K_{s43}^{N}\beta _{Ls\mathrm{B}} + K_{s44}^{N} - \mathrm{i}\omega _{s}g_{s\mathrm{B}} / c_{s} \right )\gamma _{Ls\mathrm{B}}, $$

(84)

$$ D_{s44} = \left [ - K_{s43}^{N} + \left ( K_{s44}^{N} + 2\mathrm{i}\mu _{\mathrm{B}}\omega _{s} / c_{s} \right )\beta _{Ts\mathrm{B}} \right ]\gamma _{Ts\mathrm{B}}. $$

(85)