1 Introduction

While erosion and sedimentation are natural processes, the rate of these mechanisms may be dramatically accelerated through urbanization and human activities that destabilize soils and alter stream dynamics. As anthropogenic components of river systems, reservoirs are constructed to retain water for various purposes such as irrigation, hydroelectric power generation, drinking water supply, and flood control. Reservoirs are inevitably prone to sedimentation due to regulated flow conditions (relatively low flow velocity and turbulence) and a limited sediment transport capacity. The progressive process of sedimentation occurs at varied rates, depending on a variety of factors, such as hydrological features of the catchment and river basin characteristics [1]. Thus, reservoir sedimentation is a major issue in areas with substantial sediment yield [2]. Sediment accumulation in reservoirs decreases the storage capacity over time, which, in fact, cuts down their useful lifespan, poses safety issues, and limits the advantages provided by dams and reservoirs [3].

The mean annual loss of global storage owing to sedimentation surpasses the growth in capacity by constructing new reservoirs [4, 5]. Following the 1987 World Bank report, it has been frequently stated in the literature that sediment deposition in reservoirs reduces the global storage capacity by 0.5–1% annually [6, 7]. Consequently, to ensure the long-term viability and sustainability of reservoirs, it is of critical importance to implement appropriate management strategies that include measures to minimize the catchment sediment yield and its inflow to reservoirs, as well as adopting sediment removal techniques [8, 9].

Reservoir flushing has been recognized as one of the most cost-effective desiltation methods [10]. By sufficiently lowering the reservoir water level (drawdown flushing), higher flow velocities and flow-induced shear forces imposed on deposits cause the mobilization and transport of particles. The excessive volume of flushed-out particles and high suspended sediment concentration may impair the integrity of the downstream ecosystem, including negative morphological effects, such as river bed clogging. Hence, assessing the compatibility of sediment flushing activities with the preservation of the downstream environment is indispensable. The flushing efficiency is determined by various factors, including sediment characteristics, the discharge and water levels within the reservoir, the reservoir geometry as well as the size and location of outlets, among others. Although there are different indicators in the literature to evaluate the effectiveness of flushing events, such as the sediment balance ratio or the long-term capacity ratio, there is no unified approach and criterion based on which to quantify flushing effectiveness [11].

Numerical models that replicate hydro-morphodynamic processes are beneficial tools for predicting the consequences of flushing operations. The application of numerical simulations to study sediment dynamics and flushing events is well documented in the literature. Depending on the available computational power, features of the study region, and the appropriate level of numerical simplification, researchers have employed a variety of modeling techniques to simulate reservoir flushing events, i.e., 1D [12, 13], 2D [14, 15], 3D [16, 17], and mesh-free Lagrangian models [18]. However, unless a reservoir is characterized as straight and narrow, the three-dimensional behavior of the flow, such as secondary currents in bends, needs to be considered. Although numerical models are promising tools for simulating reservoir flushing, there is a considerable challenge posed by uncertainties arising from the imperfect structure of the model reflecting the nature (i.e., model approximations and simplifications), initial assumptions and boundary conditions, equations derived from limited experimental/field studies, as well as imprecise, sparse and erratic data and measurements for model calibration/validation [19]. Hydro-morphodynamic numerical models are characterized by a large number of input parameters, some of which are physically impractical to be measured, while others can only be quantified at certain places over a limited period. Hence, within the calibration process, uncertain input variables that significantly impact model accuracy and predictive dependability are adapted in a way that simulated values correspond to their measured pairs with a reasonable tolerance.

Most of the related studies on numerical modeling of reservoir flushing have investigated individual parameters in the case of model calibration by manual trial-and-error and one-at-a-time (OAT) approach based on the user’s comprehension of the model structure and properties of the environmental system. In other words, the general approach among the researchers in this field for model calibration is to examine each sensitive parameter independently while kee** the others constant. In practice, however, the overall optimum fit may not emerge from the combination of the best values of each component individually. It means there may be a significant conflict between the evaluated parameters, where by using manual OAT calibration, their trade-offs cannot be quantified. As a result, when handling a complex model with many unknown input parameters, the manual calibration approach becomes demanding and time-consuming, involving a high degree of subjectivity. Thus, using optimization methods to accomplish the model fitting procedure is a cutting-edge alternative. Although automatic model calibration has been widely used in various fields of environmental research over the last few decades, such as groundwater or hydrological models, its application to hydro-morphodynamic models is relatively new and limited, indicating a considerable research gap. Related studies in this field mainly focused on using stochastic metaheuristic optimization algorithms [20] as well as Bayesian calibration techniques [21]. Such methods incorporate randomness or probabilistic elements in their core operations to explore the solution space. Nevertheless, the calibration time associated with these methods is significantly high due to the numerous model runs for sampling the entire search space. An approach to overcome this challenge is to use a representative metamodel (surrogate model), which replaces the numerical model and replicates its output trends [22]. However, it should be noted that metamodels are just an approximation of the full-complexity numerical models and may only be employed for accelerating the calibration procedure if sufficient model runs (training iterations) are performed to construct the metamodel. The other alternative for automatic calibration is to use deterministic gradient-based optimization algorithms, which interact directly with the numerical model and require much fewer model runs compared to the sampling-based approaches.

In this study, the flushing operation of the Bodendorf reservoir in Austria is simulated with a fully 3D numerical model. The model is coupled with a gradient-based optimization algorithm and automatically calibrated against the measured flushed bed levels of 10 cross-sections along the reservoir. This work aims to assess the applicability and efficiency of automatic model calibration for reservoir flushing events.

2 Materials and methods

2.1 Study area

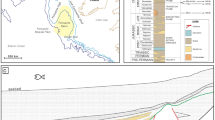
The Bodendorf run-of-the-river power plant, with an installed capacity of 7.5 MW and an annual production of about 33 GWh, was constructed between 1979 and 1982 on the River Mur in the federal state of Styria in Austria (47° 06′ 27″ N, 14° 03′ 54″ E) (Fig. 1). The reservoir is about 2.5 km long, has an average width of 40 m (between 35 and 120 m), an average slope of 3.8 ‰ (between 0.5 and 7 ‰), and a designed storage capacity of 900,000 m3. The weir system, used for drawdown flushing, consists of two radial gates with an attached top flap. The width and height of each gate are 12 m and 8.5 m, respectively. The average annual amount of siltation is estimated to be approximately 35,000 m3 [23].

Fig. 1
figure 1

a and b Austria (green) and the catchment area (red) that covers parts of the federal states Styria and Salzburg, c and d the river network and elevation map of the catchment, and e aerial photo of the Bodendorf reservoir

Full size image

Since the first flushing operation in 1996, the reservoir has been subject to regular flushings. To develop sustainable reservoir management strategies for alpine reservoirs, comprehensive monitoring of the Bodendorf reservoir flushing was performed in 2004 within the framework of the EU Interreg IIIB project ALPRESERV, also considering ecological impacts on the downstream river section [24]. The duration of the 2004 flushing was 31 h, where the discharge reached a maximum of 134 m3/s under free flow conditions. Figure 2 depicts the flushing hydrograph together with the corresponding water level at the weir, which is used as the boundary condition for simulations.

Fig. 2
figure 2

The inflow discharge rate and the water level at the weir during the Bodendorf reservoir flushing in 2004

Full size image

According to echo sounder measurements, the flushed-out volume was about 47,300 m3 [23]. The data obtained from bathymetry surveys conducted before and after the flushing are used to set up the numerical model and for automatic calibration.

2.2 Numerical modeling

The flow during reservoir flushing typically has three-dimensional behavior, including the effect of secondary currents in curved parts and in reaches where bedforms develop. This results in complex water–sediment interactions. The fully three-dimensional numerical model SSIIM (Sediment Simulation In Intakes with Multiblock option) is used in this study to calculate the hydraulics and morphological bed changes. SSIIM solves the Reynolds-averaged Navier–Stokes (RANS) equations (Eq. 1) along with the continuity equation (Eq. 2) on an unstructured and non-orthogonal adaptive grid [25]. The model has been successfully used in prototype-scale reservoir flushing studies and has yielded promising outcomes [26,27,28,29]. SSIIM employs a finite-volume approach for spatial discretization. An implicit time discretization scheme enables the use of large time steps in the model, which, together with the presence of the adaptive grid, reduces the computational time.

$$\frac{{\partial U_{i} }}{\partial t} + U_{j} \frac{{\partial U_{i} }}{{\partial x_{j} }} = \frac{1}{\rho }\frac{\partial }{{\partial x_{j} }}\left( { - P\delta_{ij} - \rho \overline{{u_{i} u_{j} }} } \right)$$
(1)
$$\frac{{\partial U_{i} }}{{\partial x_{i} }} = 0\quad i = 1, 2, 3$$
(2)

U is the time-averaged velocity, \(x\) represents the geometrical dimension, \(\rho\) is the fluid density, \(P\) denotes the dynamic pressure, \(\delta_{ij}\) represents the Kronecker delta (\(\delta_{ij} = 1\) if \(i = j\), otherwise \(\delta_{ij} = 0\)), and \(- \rho \overline{{u_{i} u_{j} }}\) (Eq. 3) is the turbulent Reynolds stress term [30], which is modeled by the k–ε turbulence closure scheme [31] to estimate the turbulent eddy viscosity \(\nu_{T}\):

$$- \overline{{u_{i} u_{j} }} = \nu_{T} \left( {\frac{{\partial U_{i} }}{{\partial x_{j} }} + \frac{{\partial U_{j} }}{{\partial x_{i} }}} \right) - \frac{2}{3}k\delta_{ij}$$
(3)

The pressure term is computed by the semi-implicit method for pressure-linked equations (SIMPLE) based on the water continuity defect in a cell [32]. The convective term in Eq. 1 is calculated by the power law scheme. The Rhie and Chow [33] momentum interpolation for non-staggered grids is used to estimate the cell-surface flux from the cell-center calculated velocity [34]. The free water surface is modeled by an implicit method based on the diffusive wave equation [35].

A Dirichlet boundary condition is specified for the variables at the upstream boundary, and the Neumann-type zero gradient boundary condition is applied to all variables at the downstream boundary. It means that the derivative (gradient) of variables normal to the boundary is set to zero and their value at the downstream boundary is defined to be equal to the calculated value in the closest cell to the boundary. The logarithmic wall function for rough boundaries (Eq. 4) is defined for the cells close to the bed [36].

$$u = \frac{{u^{*} }}{\kappa }\ln \left( {\frac{30y}{{k_{s} }}} \right)$$
(4)

where \(u\) and \({u}^{*}\) are the flow and shear velocities, respectively, \(\kappa\) is the von Kármán constant (= 0.41),\(y\) is the distance from the center of the border cell to the wall, and \(k_{s}\) is the roughness height.

The adaptive grid covers the area between the head of the reservoir and the weir structure; hence, the modeling domain ends at the upstream side of the dam. The grid consists of 20 × 390 horizontal cells in lateral and streamwise directions, respectively, and a maximum number of 10 vertical cells at the deepest part of the reservoir. The vertical profile refinement is a function of the free water surface and bed elevation changes that arise from the applied wetting/drying algorithm. The algorithm determines the number of cells formed vertically based on the calculated water depth after each time step, allowing the computational domain to vary spatiotemporally and be modified for the following time step. tFigure 3 illustrates the computational grid used in this study.

Fig. 3
figure 3

a the computational domain of the Bodendorf reservoir and b a detailed view of the section upstream of the weir

Full size image

Suspended sediment movement is modeled by solving the transient convection–diffusion equation (Eq. 5) together with the near-bed sediment concentration. The sediment resuspension from the bed is calculated by converting the concentration into the entrainment rate.

$$ \frac{{\partial c_{i} }}{\partial t} + U_{j} \frac{{\partial c_{i} }}{{\partial x_{j} }} + \omega_{i} \frac{{\partial c_{i} }}{\partial z} = \frac{\partial }{{\partial x_{j} }}\left( {\varGamma_{T} \frac{{\partial c_{i} }}{{\partial x_{j} }}} \right) + F_{e,i}$$
(5)

where \(c_{i}\) is the concentration of the ith size class, \(\omega_{i}\) denotes the particle settling velocity, \(F_{e,i}\) is the sediment pick-up rate from erosion of ith particle from the bed, and \( \varGamma_{T} = \nu_{T} /S_{c}\) is the turbulent diffusion coefficient. By assuming the Schmidt number (\(S_{c}\)) to be equal to 1, the turbulent diffusion is set equal to the eddy viscosity (\(\nu_{T}\)). Then \(\varGamma_{T} = \nu_{T} = c_{\mu } k^{2} /\varepsilon\), where \(c_{\mu }\) is a constant equal to 0.09, k is the turbulent kinetic energy, and \(\varepsilon\) denotes the energy dissipation. To estimate the near-bed equilibrium suspended sediment concentration, the empirical formula of van Rijn [37] is used as the boundary condition (Eq. 6).

$$c_{b,i} = 0.015\frac{{d_{i} }}{a}\frac{{\left( {\frac{{\tau - \tau_{c,i} }}{{\tau_{c,i} }}} \right)^{1.5} }}{{\left( {d_{i} \left( {\frac{{\left( {\rho_{s} - \rho_{w} } \right)g}}{{\rho_{w} v^{2} }}} \right)^{\frac{1}{3}} } \right)^{0.3} }}$$
(6)

where \(c_{b,i}\) is the volumetric near-bed concentration (reference concentration) of the ith fraction, \(d_{i}\) is the particle diameter, \(a\) denotes the near-bed reference level equal to the roughness height, \(\tau\) is the bed shear stress, \(\tau_{c,i}\) represents the critical bed shear stress for initiation of motion of the ith sediment fraction, obtained from the Shields diagram, \(\rho_{s}\) and \(\rho_{w}\) are sediment and water densities, respectively, \(g\) is the acceleration of gravity, and \(v\) is the kinematic viscosity.

The bedload transport is then estimated by the empirical formulae of van Rijn [38]. Alternative sediment transport formulas tested in the current study are given by Wu [39], and Meyer-Peter and Müller [40]. The sediment transport formula gives the transport capacity that can be transformed to an equilibrium sediment concentration in a bed cell (\(c_{e}\)). The erosive (\(F_{e,i}\)) and deposition (\(F_{d,i}\)) sediment flux for size i is given in Eqs. 7 and 8, respectively.

$$F_{e,i} = c_{e,i} \omega_{i}$$
(7)
$$F_{d,i} = c_{i} \omega_{i}$$
(8)

The elevation changes in a bed cell related to the ith particle (\( \varDelta z_{i}\)) during a time step (\(\varDelta t\)) is then:

$$\varDelta z_{i} = \left( {F_{d,i} - F_{e,i} } \right)\frac{\varDelta t}{VFS}$$
(9)

The volume fraction of sediments (VFS) represents the sediment content in the bed material. The subsequent vertical movement of the grid is then computed by summing Eq. 9 over all the sediment sizes.

According to the sieve analysis of the samples collected from different sections of the Bodendorf reservoir, sediments are categorized into nine size classes for numerical modeling. The density of the sediments was set to 2.55 g/cm3. Table 1 shows the grain size distribution near the weir, middle section, and the head of the reservoir [23]. The particle distribution along the reservoir is linearly interpolated.

Table 1 Sediment characteristics used in the numerical model
Full size table

2.3 Model calibration

During calibration, the model is adapted by modifying input variables to achieve agreement between simulated and observed distributions of dependent variables. Hence, the model results should have a minimum allowable deviation from the values given in the performance criterion. The time-consuming and subjective nature of manual model calibration has prompted the development of optimization-based inverse modeling methods to expedite the procedure and establish an objective framework for model calibration. The three main elements of this approach are: one or more objective functions to quantify the discrepancies between the computed and measured values, an optimization algorithm to sample the parameter space and minimize the disagreements through iterative model runs, and a target convergence threshold to terminate iterations.

The model-independent nonlinear Parameter ESTimation and predictive uncertainty analysis tool PEST [41] is coupled with SSIIM to calibrate the models. This tool has shown satisfactory results regarding sensitivity analysis, parameter estimation, and automatic model calibration in various fields, e.g., hydraulics and sediment transport [42, 43], groundwater [44], stormwater management [45], and hydrological models [46].

PEST uses the gradient-based Gauss–Marquardt–Levenberg (GML) optimization algorithm, which solves nonlinear least-squares problems. The algorithm is a hybrid of gradient descent (first-order gradient-based) and Gauss–Newton (second-order curvature-based) methods. This combination improves efficiency by using the gradient descent method for steep regions of the objective function surface, while the algorithm acts as the Gauss–Newton method for the near-optimum shallow parts.

The relationship between input variables and model outputs is iteratively linearized by formulating a Taylor expansion of the current optimum parameter set (in the case of the first iteration, the initial user-defined values). During each optimization iteration, partial derivatives of outputs are calculated concerning input parameters by using the forward finite differences method and by running the model once for each adjustable parameter to generate an m × n Jacobian matrix (m = the number of model outputs, n = the number of parameters subject to calibration). Hence, each element of the Jacobian matrix Jij contains the derivative of the ith output with respect to the jth parameter. The new parameter set can then be found by solving the linearized problem. By comparing the objective function value obtained from the latest iteration with those achieved in prior ones, PEST identifies whether another optimization iteration is required; if so, the procedure is repeated until the termination criteria are met. The GML algorithm aims to minimize the sum of the squares of the errors between predictions and observations as the objective function (\(\varPhi\)) through a sequence of parameter update vectors (\(u_{up}\)) within the user-specified bounds.

$$\varPhi = \left( {y - y^{\prime}} \right)^{T} W\left( {y - y^{\prime}} \right) = \mathop \sum \limits_{i = 1}^{m} \left( {w_{i} r_{i} } \right)^{2}$$
(10)
$$u_{up} = \left( { J^{T} W J + \lambda I} \right)^{ - 1} J^{T} Wr$$
(11)

where \(y\) and \(y^{\prime}\) are vectors of order m that hold observations and calculated values, respectively, \(W\) is an m-dimensional diagonal matrix containing squared observation weights \(w_{i}\) (which are taken to be 1 in this study), the superscript \(T\) represents matrix transpose, and \(r_{i}\) is the residual of the ith calculated-observed pair (in this study, bed elevations). The parameter upgrade vector \(u_{up}\) is calculated in accordance with \(J\) = Jacobian matrix containing the derivatives of simulated values with respect to the calibration parameters, \(\lambda\) = Marquardt lambda as a dam** factor, \(I\) = an n-dimensional identity matrix, and \(r\) = the vector of residuals.

The termination criterion for the optimization algorithm is set in a way that if the relative change of the objective function (\(\left( {\varPhi_{i} - \varPhi_{min} } \right)/\varPhi_{i}\)) is less than 0.005 over the four successive iterations, the algorithm stops the inversion process (\(\varPhi_{i}\): objective function value at the end of the ith iteration; \(\varPhi_{min}\): the lowest value of the objective function achieved so far during the whole optimization procedure) [41].

2.4 Calibration parameters

The response of a model to particular input parameter alteration needs to be analyzed in many modeling applications to determine how sensitive it reacts to adjustments. This may serve as the initial stage of the model calibration procedure, whereby key variables are determined. The sensitivity analysis in this study is performed by the SENSitivity ANalyzer tool (SENSAN), as a subset of the PEST program. The sensitivity of simulation results to parameter adjustments is tracked and recorded by successive model runs conducted by SENSAN using specified sets of parameter values. In this study, the following parameters show significant influence on the results and are selected for automatic calibration.

  1. 1.

    Parameters in van Rijn’s bedload transport formula (\(\alpha_{1}\), \(\alpha_{2}\),\(\alpha_{3}\),\(\alpha_{4}\)):

    $$q_{b} = \alpha_{1} \sqrt {\Delta g} \frac{{ T^{{\alpha_{2} }} }}{{D_{*}^{{\alpha_{3} }} }} d_{50}^{{\alpha_{4} }}$$
    (12)

    \(q_{b}\) gives the bedload transport rate for particle size range 0.2 ≤ d ≤ 2 mm.

    • \(\Delta\) is the submerged relative density of sediments (\(= \frac{{\rho_{s} - \rho_{w} }}{{\rho_{w} }}\)),

    • \(T\) is the transport stage parameter (\(= \frac{{\tau - \tau_{c} }}{{\tau_{c} }}\)),

    • \(D_{*}\) is known as the particle number (\(= d_{50} \left( {\frac{\Delta g}{{v^{2} }}} \right)^{\frac{1}{3}}\)),

    • \(\alpha_{1}\), \(\alpha_{2}\),\(\alpha_{3}\),\(\alpha_{4}\) are variables in the van Rijn equation and have the following values in the original formula: 0.053, 2.1, 0.3, 1.5, respectively.

  2. 2.

    Coefficient of Meyer-Peter and Müller’s (MPM) sediment transport formula (\(\beta\)):

    $$\phi_{b} = \beta \left( {\tau^{*} - \tau_{c}^{*} } \right)^{1.5}$$
    (13)

    where \(\tau^{*}\) and \(\tau_{c}^{*}\) are the bed shear stress and the critical bed shear stress in dimensionless form, respectively. This equation gives the bedload transport intensity verified with experimental data for uniform coarse sand and gravel. The original recommended value for the coefficient is \(\beta\) = 8. The contribution of other researchers to modify this formula based on different conditions and experimental data can be found in the literature, e.g., \(\beta\) = 5.7 [47] or \(\beta\) = 12 [48].

  3. 3.

    Hiding-exposure parameter (\(\xi\)):

    The hiding-exposure effect of nonuniform sediments is calculated by Wu’s correction factor (\(\eta_{i}\)) for the critical bed shear stress, based on the probabilities of hiding (\(p_{Hi}\)) and exposure (\(p_{Ei}\)) of the ith size fraction, which is stochastically related to the sediment size and gradation.

    $$\eta_{i} = \left( {\frac{{p_{Hi} }}{{p_{Ei} }}} \right)^{\xi }$$
    (14)

    the parameter \(\xi\) was originally calibrated using laboratory and field data, and a value of \(\xi = 0.6\) was suggested.

  4. 4.

    Effective bed roughness height (ks) can be defined as the sum of the grain roughness (skin friction) and the bedform-induced resistance (form friction).

    $$k_{s} = 3d_{90} + 1.1\Delta_{d} \left( {1 - e^{{\left( { - 25\frac{{\Delta_{d} }}{{\lambda_{d} }}} \right)}} } \right)$$
    (15)

    where \(d_{90}\) is the characteristic sediment size, and \(\Delta_{d}\) and \({\uplambda }_{d}\) are bedform height and length, respectively.

  5. 5.

    Active layer thickness (ALT) is the height of the erodible bed layer, where grain sorting and exchange processes occur, i.e., entrainment and deposition of sediments. The thickness of this layer is usually attributed to the representative grain diameter or the bedform height, depending on the transport regime. The value for this parameter in the numerical model defines the maximum erodible depth within a time step.

  6. 6.

    The volume fraction of sediments (VFS) is a parameter to define the proportion of sediments to the water content in the bed deposit. Hence, it can also be expressed as one minus the porosity of the bed material. In the model, a single value is used for the entire modeling domain.

Table 2 summarizes the investigated parameters with their starting values, as well as the maximum and minimum boundary values introduced to the optimization algorithm.

Table 2 Parameters for calibration with their initial values and allowable variation range
Full size table

The numerical models are calibrated against the measured bed elevations in 10 cross-sections along the reservoir (about 1300 measured points). Figure 4 depicts the location of the cross-sections.

Fig. 4
figure 4

The location of cross-sections with measured bed elevations used for calibration

Full size image

3 Results and discussion

3.1 Calibrated values

The GML optimization algorithm is applied to three computational models using different sediment transport formulae. It ought to be mentioned that the GML algorithm, as a gradient-based optimization algorithm, initiates the search process from a single point on the objective function surface (i.e., using the initial values presented in Table 2); thus, this approach may lead to the solution getting trapped in local minima points over the search space instead of converging to the global minimum. Therefore, to validate the results, reassessing the calibration procedure with sampling-based optimization algorithms is beneficial. However, it is important to note that such algorithms may require significantly more iterations to sample the entire surface of the objective function and become impractical and inefficient for computationally expensive models, such as models simulating the hydro-morphological processes. The calibration results for the parameters mentioned in Sect. 2.4 are presented in Table 3. The number of model runs varies depending on the number of adjustable parameters since one run per parameter is required to build the Jacobian matrix within each optimization iteration. The lowest number of model runs is for Wu (62 runs), and the highest is for van Rijn (110 runs). The bedload transport formulae of van Rijn and Meyer-Peter and Müller (MPM) can be revised by replacing the values of \(\alpha_{i}\) and \(\beta\) from Table 3 into Eqs. 12 and 13. Regarding van Rijn’s formula, all parameters except \(\alpha_{4}\), have higher values compared to the original formula. The relative change is in the range of 5 to 25%. The coefficient \(\beta\) in the MPM formula is slightly higher than the recommended value (8.9 compared to 8), resulting in a higher transport rate.

Table 3 Results of the three calibrated models using different sediment transport formulae
Full size table

The hiding and exposure parameter is found to be almost half of the recommended (\(\xi = 0.6\)) value for all three models. The calibrated values for roughness are in the range between 21 and 29 cm, while the active layer thickness has a wide variation range (30–50 cm). The volume fraction of sediments is almost 60% for the models of van Rijn and MPM, whereas a value of 40% yields the best result for the model calculated by Wu’s formula.

According to Table 3, it should be noted that the calibrated values are entirely model-dependent, and an identical optimized parameter combination may not be the best set if a model feature is changed. It means calibrating a hydro-morphodynamic model and then applying the optimized values to the same model with a different sediment transport formula, which is a common approach when following the manual model calibration, does not necessarily lead to the best result.

3.2 Statistical performance of the models

To provide a quantitative and comparative evaluation of the model’s capability to predict bed level changes, the deviation between calculated and measured bed elevations after flushing is assessed by several statistical indicators (Table 4). As a bias predictor, mean bias error (MBE) shows the model under- or over-estimation. Root mean squared error (RMSE) and mean absolute error (MAE) reflect the average error magnitude. While MAE shows a linear trend of individual errors, RMSE is dominated by large deviations, i.e., it emphasizes big errors by assigning them larger weights and is more sensitive to outliers. Kling–Gupta efficiency (KG) is applied as a composite goodness-of-fit metric, integrating correlation, variability, and bias into a single objective function. It is defined as the geometric mean of the Pearson correlation coefficient, the ratio of the standard deviation of predicted values to observations, and the ratio of the simulation mean to the observation mean. The Brier skill score (BSS), which measures the performance of simulations relative to a reference or baseline prediction (initial bed levels before flushing), is also used. BSS compares the mean squared error (MSE) between the simulation and observation with the MSE between the baseline prediction and observation. The range for BSS is between − ∞ and 1.

Table 4 Overall statistical performance of the automatically calibrated models regarding bed level changes with different bedload transport formulae
Full size table

The negative value of MBE for the van Rijn model shows the overprediction of the bed erosion, while the other two models underpredict the eroded sediments by having positive values. According to their lower MAE and RMSE values, the models using the formulae of van Rijn and Wu have better performance than the model using the formula of MPM. This can further be confirmed by higher values of the Kling–Gupta efficiency and Brier skill score of van Rijn and Wu models. According to van Rijn et al. [49], a value of 0.3 ≤ BSS ≤ 0.6 shows a “reasonable/fair” model prediction. The prediction can be stated as “good” if the value is in the range of 0.6–0.8. Models having BSS values over 0.8 or under 0.3 have “excellent” or “poor” performance, respectively. In the case of a negative value, the model has a “bad” performance. Therefore, both models simulated by the formulae of van Rijn and Wu can be called “good” predictors of the flushing event in this study. The model calculated by the MPM bedload formula also gives a “reasonable/fair” result.

3.3 Bed level changes

Figure 5 shows measured bed elevations in 10 cross-sections before and after flushing together with the bed levels from the three automatically calibrated models. The statistical metrics presented in Sect. 3.2 are also used to evaluate the cross-sectional bed level changes (Table 5).

Fig. 5
figure 5

Simulated bed levels of the Bodendorf reservoir after flushing using the formulae of Meyer-Peter and Müller (MPM), van Rijn, and Wu in 10 cross-sections, including the measured bed levels before and after flushing

Full size image
Table 5 Cross-sectional goodness-of-fit for models using different bedload transport formulae
Full size table

Although the pattern of calculated bed levels after flushing for all three models agrees well with their measured pairs, slight local discrepancies can be seen in some cross-sections. Looking at the most upstream-located cross-section (A–A), the small eroded part at the orographic right river bank cannot be seen in the simulations. In section B–B, a steep drop at the right bank with a sharp rise toward the center can be noticed in the measured bed pattern, which is not the case for the results of the numerical models. This reverse fluctuating pattern compared to the initial bed can be attributed to the occurrence of the lateral sand slide, which is approximated by the program but cannot be resolved [50]. Here, almost the same volume of sliding sediments is deposited in the middle part. Furthermore, cross-section B–B has the highest simulated bed level deviation from the measured data according to MAE and RMSE values in Table 5.

The discrepancies between simulation results and the observed bed pattern after flushing in cross-section C–C can be seen at the left and right edges of the flushing channel, where measurements show an extended channel widening close to the reservoir banks. Particularly for the model using the formula of MPM, the results show an about 1-m bed elevation difference compared to the measurement at distances of 60 and 90 m along the cross-section. A similar issue regarding the depth and width of the eroded part persists for cross-section D–D at the left side and for cross-sections E–E, F–F, G–G, and H–H at the left and right edges of the flushing channel. For the aforementioned sections, the model using the formula of van Rijn gives the closest simulated patterns to the measurements, which can be confirmed by the lowest MAE and RMSE as well as the highest KG and BSS values of the van Rijn model presented in Table 5.

The calculated patterns for two cross-sections adjacent to the weir (I–I and J–J) are almost identical to those observed. Slight differences can be noticed at the left slope of cross-section I–I simulated by the MPM model, as well as the right slope and central part of cross-section J–J calculated by the van Rijn model. Although the predicted bed patterns by all three models are similar in these two cross-sections (almost similar KG efficiency values according to Table 5), other statistical metrics reveal the better performance of the Wu model.

3.4 Flushed volume

The total flushed volume of sediments (presented in Table 3) confirms the trend of over- or underestimation of erosion, which can be seen in the cross-sections in Fig. 5. Compared to the measured flushed volume of 47,300 m3, van Rijn’s model overestimates the erosion (52,200 m3), whereas underestimations are found by the models of MPM and Wu (37,800 m3 and 43,900 m3, respectively). The deviation between calculated and measured flushed volumes is about ± 10% for van Rijn and Wu models and − 20% for MPM.

4 Conclusions

This study employs an automatically calibrated 3D numerical model of the Bodendorf reservoir to simulate the 2004 flushing event. The bed level changes and the volume of flushed sediments are calculated using the formulae of Meyer-Peter and Müller, van Rijn, and Wu. Prior to calibration, a sensitivity analysis is performed to detect the most affecting parameters in the model (i.e., the roughness height, active layer thickness, volume fraction of sediments in bed, hiding-exposure parameter, and empirical factors in the formulae of van Rijn and MPM). The measured bed elevation data from 10 cross-sections (about 1300 points) along the reservoir is used for calibration. The optimization algorithm runs the models several times based on the number of parameters subject to calibration. The formulae of van Rijn and MPM are modified during the optimization by finding new values for their empirical parameters. The parameter regarding the hiding-exposure behavior of nonuniform sediments introduced by Wu is also modified by a factor of 0.5. The calibration results for the roughness height, active layer thickness, and the volume fraction of sediments are found to be model-dependent, where different sediment transport formulae yield a unique parameter combination leading to an optimized outcome.

The performance of the calibrated models is investigated by different statistical metrics. According to the mean absolute error, root mean squared error, and Kling–Gupta efficiency, the models using the formulae of van Rijn and Wu outperform the model calculated by the MPM formula in terms of error amount and correlation. The two former models show almost equal performance, and no clear statistical evidence of superiority exists among them. This is also confirmed by the Brier skill score, where both van Rijn and Wu models have almost the same score, indicating their “good” performance. According to the evaluation criteria of the Brier skill score, the model simulated by the MPM formula has a “reasonable/fair” performance.

Patterns of simulated bed elevations in 10 cross-sections are compared with the measured data, which are in good agreement with the observations. The discrepancies are limited to the local differences as a result of sand slides in the two most upstream cross-sections, as well as the underestimation of lateral erosion and widening of the flushing channel at middle cross-sections of the reservoir, especially those predicted by the model using the MPM formula. The calculated flushed volume of sediments shows a reasonable agreement (approximately ± 10% regarding van Rijn and Wu models and − 20% for MPM) compared to the measured flushed volume of 47,300 m3.

This study provides an overview of applying automatic calibration for hydro-morphodynamic models in a prototype scale and shows how the best fit can be objectively achieved. According to the number of model runs and considering innumerable parameter combinations, it can be concluded that employing optimization algorithms is a suitable and efficient alternative for the widely used subjective trial-and-error calibration approach.

To improve the validity and reliability of the automatic calibration, future work can include a multi-objective optimization approach to consider additional aspects of the model, e.g., measured downstream sediment concentrations during the flushing event to define a second objective function in addition to the bed level changes. Then, instead of achieving a single value for investigated uncertain parameters, a set of equally good and non-dominated solutions (Pareto front) can be found, which would be interesting to be compared with the results of the single-objective method. A challenge in this regard is related to using global optimization algorithms, which require orders of magnitude more model runs for sampling the entire objective function surface. However, the issue can be tackled by applying surrogate modeling techniques [51].