Abstract
Methods for finding pure Nash equilibria have been dominated by variational inequalities and complementarity problems. Since these approaches fundamentally rely on the sufficiency of first-order optimality conditions for the players’ decision problems, they only apply as heuristic methods when the players are modeled by nonconvex optimization problems. In contrast, this work approaches Nash equilibrium using theory and methods for the global optimization of nonconvex bilevel programs. Through this perspective, we draw precise connections between Nash equilibria, feasibility for bilevel programming, the Nikaido–Isoda function, and classic arguments involving Lagrangian duality and spatial price equilibrium. Significantly, this is all in a general setting without the assumption of convexity. Along the way, we introduce the idea of minimum disequilibrium as a solution concept that reduces to traditional equilibrium when an equilibrium exists. The connections with bilevel programming and related semi-infinite programming permit us to adapt global optimization methods for those classes of problems, such as constraint generation or cutting plane methods, to the problem of finding a minimum disequilibrium solution. We propose a specific algorithm and show that this method can find a pure Nash equilibrium even when the players are modeled by mixed-integer programs. Our computational examples include practical applications like unit commitment in electricity markets.


Similar content being viewed by others
Data availability
The authors did not analyse or generate any datasets, because the work proceeds within a theoretical and mathematical approach.
Notes
Copyright © 2021 AIMMS B.V. All rights reserved. AIMMS is a registered trademark of AIMMS B.V. www.aimms.com.
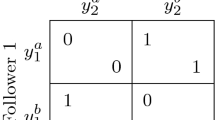
As previously noted, potential games with continuous potentials and compact strategy sets always have a pure Nash equilibrium; see for instance [38, Lemma 2.1] We will see that this example in fact does not have an equilibrium, which is another indication that this example cannot be formulated as a potential game with a well-behaved potential function.
References
Aubin, J.-P., Frankowska, H.: Set-Valued Analysis. Springer, Berlin (2009)
Bard, J.F.: An algorithm for solving the general bilevel programming problem. Math. Oper. Res. 8(2), 260–272 (1983)
Beck, M., Stein, O.: Semi-infinite models for equilibrium selection. Minimax Theory Appl. (2023)
Bertsekas, D.P.: Nonlinear Programming, 2nd edn. Athena Scientific, Massachusetts (1999)
Blankenship, J.W., Falk, J.E.: Infinitely constrained optimization problems. J. Optim. Theory Appl. 19(2), 261–281 (1976)
Burer, S.: On the copositive representation of binary and continuous nonconvex quadratic programs. Math. Program. 120(2), 479–495 (2009)
Carvalho, M., Lodi, A., Pedroso, J.P., Viana, A.: Nash equilibria in the two-player kidney exchange game. Math. Program. 161(1–2), 389–417 (2017)
Chen, S., Conejo, A.J., Sioshansi, R., Wei, Z.: Equilibria in electricity and natural gas markets with strategic offers and bids. IEEE Trans. Power Syst. 35(3), 1956–1966 (2019)
Colson, B., Marcotte, P., Savard, G.: An overview of bilevel optimization. Ann. Oper. Res. 153(1), 235–256 (2007)
Contreras, J., Klusch, M., Krawczyk, J.B.: Numerical solutions to Nash-Cournot equilibria in coupled constraint electricity markets. IEEE Trans. Power Syst. 19(1), 195–206 (2004)
Djelassi, H., Mitsos, A.: A hybrid discretization algorithm with guaranteed feasibility for the global solution of semi-infinite programs. J. Glob. Optim. 68(2), 227–253 (2017)
Djelassi, H., Mitsos, A., Stein, O.: Recent advances in nonconvex semi-infinite programming: applications and algorithms. EURO J. Comput. Optim. 9, 100006 (2021)
Dragotto, G., Scatamacchia, R.: ZERO regrets algorithm: optimizing over pure Nash equilibria via integer programming (2021). ar**v preprint ar**v:2111.06382
Facchinei, F., Kanzow, C.: Generalized Nash equilibrium problems. Ann. Oper. Res. 175(1), 177–211 (2010)
Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, New York (2003)
Facchinei, F., Pang, J.-S.: Nash equilibria: the variational approach. In: Palomar, D.P., Eldar, Y.C. (eds.) Convex Optimization in Signal Processing and Communications, chapter 12, pp. 443–493. Cambridge University Press, Cambridge (2010)
Fuller, J.D.: Market equilibrium models with continuous and binary variables. Technical report (2008). URL https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.454.1505 &rep=rep1 &type=pdf
Fuller, J.D., Çelebi, E.: Alternative models for markets with nonconvexities. Eur. J. Oper. Res. 261(2), 436–449 (2017)
Gabriel, S.A., Conejo, A.J., Fuller, J.D., Hobbs, B.F., Ruiz, C.: Complementarity Modeling in Energy Markets. Springer, New York (2013)
Gabriel, S.A., Conejo, A.J., Ruiz, C., Siddiqui, S.: Solving discretely constrained, mixed linear complementarity problems with applications in energy. Comput. Oper. Res. 40(5), 1339–1350 (2013)
Gabriel, S.A., Siddiqui, S.A., Conejo, A.J., Ruiz, C.: Solving discretely-constrained Nash-Cournot games with an application to power markets. Netw. Spatial Econ. 13(3), 307–326 (2013)
GAMS Development Corporation. GAMS: General Algebraic Modeling System (2021). www.gams.com
Gribik, P.R., Hogan, W.W., Pope, S.L.: Market-clearing electricity prices and energy uplift. Technical report, Harvard Electricity Policy Group (2007). https://hepg.hks.harvard.edu/files/hepg/files/gribik_hogan_pope_price_uplift_123107.pdf
Guerra-Vázquez, F., Rückmann, J.-J., Stein, O., Still, G.: Generalized semi-infinite programming: a tutorial. J. Comput. Appl. Math. 217(2), 394–419 (2008)
Guo, C., Bodur, M., Taylor, J.A.: Copositive duality for discrete markets and games (2021). ar**v preprint ar**v:2101.05379
Gürkan, G., Pang, J.-S.: Approximations of Nash equilibria. Math. Program. 117(1), 223–253 (2009)
Harks, T., Schwarz, J.: Generalized Nash equilibrium problems with mixed-integer variables (2021). ar**v preprint ar**v:2107.13298
Harms, N., Kanzow, C., Stein, O.: On differentiability properties of player convex generalized Nash equilibrium problems. Optimization 64(2), 365–388 (2015)
Harwood, S.M., Barton, P.I.: Lower level duality and the global solution of generalized semi-infinite programs. Optimization 65(6), 1129–1149 (2016)
Harwood, S.M., Trespalacios, F., Papageorgiou, D.J., Furman, K.: Equilibrium modeling and solution approaches inspired by nonconvex bilevel programming (2021). ar**v preprint ar**v:2107.01286v2
Kirst, P., Stein, O.: Global optimization of generalized semi-infinite programs using disjunctive programming. J. Glob. Optim. 73(1), 1–25 (2019)
Lampariello, L., Sagratella, S.: A bridge between bilevel programs and Nash games. J. Optim. Theory Appl. 174(2), 613–635 (2017)
Li, H., Meissner, J.: Competition under capacitated dynamic lot-sizing with capacity acquisition. Int. J. Prod. Econ. 131(2), 535–544 (2011)
Mitsos, A.: Global solution of nonlinear mixed-integer bilevel programs. J. Glob. Optim. 47(4), 557–582 (2010)
Mitsos, A.: Global optimization of semi-infinite programs via restriction of the right-hand side. Optimization 60(10–11), 1291–1308 (2011)
Mitsos, A., Tsoukalas, A.: Global optimization of generalized semi-infinite programs via restriction of the right hand side. J. Glob. Optim. 61(1), 1–17 (2015)
Mitsos, A., Lemonidis, P., Barton, P.I.: Global solution of bilevel programs with a nonconvex inner program. J. Glob. Optim. 42(4), 475–513 (2008)
Monderer, D., Shapley, L.S.: Potential games. Games Econ. Behav. 14(1), 124–143 (1996)
Nagurney, A.: Spatial price equilibrium, perishable products, and trade policies in the Covid-19 pandemic. Montes Taurus J. Pure Appl. Math. 4(3), 9–24 (2022)
Nash, J.: Equilibrium points in n-person games. Proc. Natl. Acad. Sci. 36(1), 48–49 (1950)
Nikaidô, H., Isoda, K.: Note on non-cooperative convex games. Pac. J. Math. 5(Suppl. 1), 807–815 (1955)
Pang, J.-S., Scutari, G.: Nonconvex games with side constraints. SIAM J. Optim. 21(4), 1491–1522 (2011)
Papageorgiou, D.J., Trespalacios, F., Harwood, S.: A note on solving discretely-constrained Nash–Cournot games via complementarity. Netw. Spatial Econ. 21, 1–6 (2021)
Papageorgiou, D.J., Harwood, S.M., Trespalacios, F.: Pooling problems under perfect and imperfect competition. Comput. Chem. Eng. 169, 108067 (2023). https://doi.org/10.1016/j.compchemeng.2022.108067
Sagratella, S.: Computing all solutions of Nash equilibrium problems with discrete strategy sets. SIAM J. Optim. 26(4), 2190–2218 (2016)
Sagratella, S.: On generalized Nash equilibrium problems with linear coupling constraints and mixed-integer variables. Optimization 68(1), 197–226 (2019)
Sahinidis, N.V.: BARON 19: Global Optimization of Mixed-Integer Nonlinear Programs, User’s Manual (2019)
Samuelson, P.A.: Spatial price equilibrium and linear programming. Am. Econ. Rev. 42(3), 283–303 (1952)
Schiro, D.A., Zheng, T., Zhao, F., Litvinov, E.: Convex hull pricing in electricity markets: formulation, analysis, and implementation challenges. IEEE Trans. Power Syst. 31(5), 4068–4075 (2015)
Schwarze, S., Stein, O.: A branch-and-prune algorithm for discrete Nash equilibrium problems. Comput. Optim. Appl. (2023). https://doi.org/10.1007/s10589-023-00500-4
Stein, O.: How to solve a semi-infinite optimization problem. Eur. J. Oper. Res. 223(2), 312–320 (2012)
Stein, O., Still, G.: On generalized semi-infinite optimization and bilevel optimization. Eur. J. Oper. Res. 142(3), 444–462 (2002)
Stein, O., Still, G.: Solving semi-infinite optimization problems with interior point techniques. SIAM J. Control Optim. 42(3), 769–788 (2003)
Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103, 225–249 (2005)
Tsoukalas, A., Rustem, B., Pistikopoulos, E.N.: A global optimization algorithm for generalized semi-infinite, continuous minimax with coupled constraints and bi-level problems. J. Glob. Optim. 44(2), 235–250 (2009)
Turan, E.M., Jäschke, J., Kannan, R.: Optimality-based discretization methods for the global optimization of nonconvex semi-infinite programs (2023). ar**v preprint ar**v:2303.00219
Ui, T.: A Shapley value representation of potential games. Games Econ. Behav. 31(1), 121–135 (2000)
Uryas’ev, S., Rubinstein, R.Y.: On relaxation algorithms in computation of noncooperative equilibria. IEEE Trans. Autom. Control 39(6), 1263–1267 (1994)
von Heusinger, A., Kanzow, C.: Optimization reformulations of the generalized Nash equilibrium problem using Nikaido–Isoda-type functions. Comput. Optim. Appl. 43(3), 353–377 (2009)
Acknowledgements
The authors would like to thank their colleague Nicolas Sawaya for introducing some of the challenges associated with equilibrium modeling within a real-world setting, as well as the various fruitful discussions on this topic over the past several years. The authors would also like to thank their colleagues Myun-Seok Cheon and Youngdae Kim for similarly fruitful discussions while develo** this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest.
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Alternate derivation and connections with the Nikaido–Isoda function
Optimization formulations of equilibrium problems have been presented in the literature before. Many rely on the Nikaido–Isoda (NI) function, first proposed by [41]; see also [14, 59] for recent treatments and generalizations. We give an alternate proof of Proposition 1 using the NI function approach, which some readers might find more intuitive.
Recall the game \(\widehat{{\mathcal {G}}}(\left( h_i,H_i \right) _{i\in \left\{ 0,1,\dots ,m \right\} })\) from Sect. 2.2.2; player i is defined by
and \((y_0^*, \dots , y_m^*)\) is a GNE of \(\widehat{{\mathcal {G}}}(\left( h_i,H_i \right) _{i\in \left\{ 0,1,\dots ,m \right\} })\) if \( y_i^* \in T_i(y_{-i}^*), \) for all \(i \in \left\{ 0,1,\dots ,m \right\} \). For \(y = (y_0, y_1, \dots , y_m)\), define
The objective function in this optimization problem defining \(\phi \) is the NI function as defined by [14, 59]. Theorem 3.2 of [14] states that \(y^* = (y_0^*, y_1^*, \dots , y_m^*)\) is a GNE of \(\widehat{{\mathcal {G}}}(\left( h_i,H_i \right) _{i\in \left\{ 0,1,\dots ,m \right\} })\) if and only if \(\phi (y^*) = 0\) and
At this point, we could define minimum disequilibrium for the game \(\widehat{{\mathcal {G}}}(\left( h_i,H_i \right) _{i\in \left\{ 0,1,\dots ,m \right\} })\) as a point \(y^*\) satisfying (13), regardless of its objective value. We will see that this agrees with, and leads to, the concept introduced in the main text.
To use this characterization of equilibrium, consider the problem of finding a scPNE of \({\mathcal {G}}(G,\left( g_i,Y_i \right) _{i\in I})\), and following the discussion in Sect. 2.2.2 we obtain an equivalent game \(\widehat{{\mathcal {G}}}(\left( h_i,H_i \right) _{i\in \left\{ 0,1,\dots ,m \right\} })\) where \(H_0 \equiv \left\{ (y_{-0}, y_0): (y_0, y_1, \dots , y_m) \in G \right\} \), \(H_i \equiv \left\{ (y_{-i}, y_i): y_i \in Y_i \right\} \), \(h_i(y_{-i}, y_i) \equiv g_i(y_0, y_i)\), and \(h_0\) is identically zero. With this, we can express the feasible set of (13) in terms of the set G and data of the (\({\mathcal {A}}_i\)) problems as
which coincides with the feasible set of Problem (\({{\mathcal {M}}}{{\mathcal {D}}}\)) (defining \(x \equiv y_0\)). Using the definition of the \(h_i\) (and the fact that \(h_0\) is identically zero), we transform \(\phi \) into
For \(y \in \Phi \), the infimum above is over a nonempty set, and furthermore, does not depend on the \(z_0\) variable. Consequently, we can ignore the side constraints encoded in G and decompose the minimization. Thus, for \(y \in \Phi \), the expression for \(\phi (y)\) simplifies to
where we recall the optimal player value function \(g_i^*\) defined in Equation (1). Finally, note that this expression equals the objective function of Problem (\({{\mathcal {M}}}{{\mathcal {D}}}\)) when \(\mu : w \mapsto {{\,\mathrm{\textstyle {\sum }}\,}}_i w_i\). Thus, Problems (\({{\mathcal {M}}}{{\mathcal {D}}}\)) and (13) coincide, and the statement that \(y^*\) is an equilibrium iff \(\phi (y^*) = 0\) and \(y^* \in \arg \min \left\{ \phi (y): y \in \Phi \right\} \), essentially provides an alternate proof of Proposition 1.
B Proof of Theorem 1
One effect of solving the player problems inexactly is that the lower bounds (at worst) converge to the optimal value of the relaxation
By defining \(w_i' = w_i - \eta _i^*\) and re-writing the objective as \({{\,\mathrm{\textstyle {\sum }}\,}}_{i\in I} (g_i(x,y_i) - w_i' - \eta _i^*)\) we see that
Similarly, the upper bounds will only reach within \(\sum _i \eta _i^*\) of \(\delta \). The following proof makes this precise. We repeat the statement of Theorem 1 here for convenience.
Theorem
Assume that the set
is compact and nonempty. Assume that for each i, \(g_i\) is continuous and \(Y_i\) is compact. Let \(\epsilon ^* = \limsup _{k \rightarrow \infty } \epsilon ^k\) and \(\eta _i^* = \limsup _{k\rightarrow \infty } \eta _i^k\) for each i. Then for any \(\varepsilon > \epsilon ^* + 2 {{\,\mathrm{\textstyle {\sum }}\,}}_{i \in I} \eta _i^*\), Algorithm 1 produces an \(\varepsilon \)-optimal solution \((x^*,y^*)\) of Problem (\({{\mathcal {M}}}{{\mathcal {D}}}'\)) in finite iterations.
Proof
We establish that the upper and lower bounds converge to some values \(\delta ^{U,*}\) and \(\delta ^{L,*}\), respectively, such that \(\delta ^{L,*} \le \delta \le \delta ^{U,*}\) and \(\delta ^{U,*} - \delta ^{L,*} \le \epsilon ^* + 2{{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^*\).
To begin, we show the the approximate solutions of the lower bounding problem (4) have a subsequence that converge to a feasible point of the relaxation (14). Let \(\left( (x^k,y^k,w^k) \right) _{k \in {\mathbb {N}}}\) be the sequence of feasible solutions of Problem (4) produced by Algorithm 1. Since more elements are added to \(Y_i^{L,k}\) at each iteration, the part of the solution sequence \(\left( w_i^k \right) _{k}\) is non-increasing, but bounded below by the minimum of \(g_i\) on \(F\); continuity and compactness ensure that this is finite (specifically, \(\inf _{x,y,z_i} \left\{ g_i(x,z_i): z_i \in Y_i, (x,y) \in F \right\} > -\infty \)). Thus, for each i, \(\left\{ w_i^k: k \in {\mathbb {N}} \right\} \) is contained in a compact set, and so the entire solution sequence is in a compact set. For each i, let \(\left( z_i^k \right) _{k \in {\mathbb {N}}}\) be the corresponding sequence of approximate solutions to the player problem (\({\mathcal {A}}_i\)); these must exist at each iteration k by continuity of \(g_i\) and compactness of \(Y_i\). Again, the image of this sequence \(\left\{ z_i^k: k \in {\mathbb {N}} \right\} \) is in a compact set (\(Y_i\)) for each i. Consequently, we have that a subsequence of solutions converges to some point. Abusing notation, we have that \((x^k,y^k,w^k) \rightarrow (x^*,y^*,w^*)\) and \(z^k \rightarrow z^*\). Note that we have \((x^*,y^*) \in F\).
Now, we establish that \((x^*,y^*,w^*)\) is feasible in the relaxation (14). Since \(z_i^k\) is added to \(Y_i^{L,k}\) at the end of each iteration, we have for each i
By taking the limit over \(\ell \), and then the limit over k, we get for each i
Now, for a contradiction, assume that for some i, \(w_i^* > g_i^*(x^*) + \eta _i^*\), indicating that \((x^*,y^*,w^*)\) is not feasible in Problem (14). This means that there exists \(z_i^{\dagger } \in Y_i\) (feasible in the player problem) with
By definition of \(z_i^k\) as an approximate minimizer of (\({\mathcal {A}}_i\)) for \(x = x^k\), we have \(g_i(x^k, z_i^{\dagger }) + \eta _i^k \ge g_i(x^k, z_i^{k})\) for all k, and taking the limit superior over k we get
Combined with Inequality (16) this gives
which contradicts (15). Thus, \((x^*,y^*,w^*)\) is feasible in Problem (14), and in particular, satisfies for each \(i \in I\)
Next, we focus on the lower bounds. The algorithm’s lower bound is constructed as

and so forms a non-decreasing sequence. From the approximate solution of the lower bounding problem (4), we have  . A simple induction argument establishes that \(\delta ^{L,k} \le \delta \) for all k, and so
. A simple induction argument establishes that \(\delta ^{L,k} \le \delta \) for all k, and so
Since we have  for all k, it follows
for all k, it follows  for all k. By construction,
for all k. By construction,  for all k, and so we have \(\limsup _{k\rightarrow \infty } ({\bar{\delta }}^{L,k} - \delta ^{L,k}) \le \limsup _{k\rightarrow \infty } \epsilon ^k \equiv \epsilon ^*\). Note that \({\bar{\delta }}^{L,k} = {{\,\mathrm{\textstyle {\sum }}\,}}_{i} (g_i(x^k,y_i^k) - w_i^k)\) has a subsequential limit
for all k, and so we have \(\limsup _{k\rightarrow \infty } ({\bar{\delta }}^{L,k} - \delta ^{L,k}) \le \limsup _{k\rightarrow \infty } \epsilon ^k \equiv \epsilon ^*\). Note that \({\bar{\delta }}^{L,k} = {{\,\mathrm{\textstyle {\sum }}\,}}_{i} (g_i(x^k,y_i^k) - w_i^k)\) has a subsequential limit
Combining this,
Next, we focus on the upper bounds. Note that for each i, \(g_i^*: {\mathbb {R}}^{n_0} \rightarrow {\mathbb {R}}\) is a continuous function by [1, Theorem 1.4.16]. Thus,
has a subsequential limit \({{\,\mathrm{\textstyle {\sum }}\,}}_i (g_i(x^*,y_i^*) - g_i^*(x^*))\) and by Inequality (17)
For each k, \({\bar{\delta }}^k\) is an upper bound: \({\bar{\delta }}^k \ge \delta \). Consequently, so is \({\bar{\delta }}^*\): \({\bar{\delta }}^* \ge \delta \). Rearranging Inequality (18), we have \({\bar{\delta }}^{L,*} - \epsilon ^* \le \delta ^{L,*}\). Combining these relations, we get:
Thus, \(\left( {\bar{\delta }}^k \right) _{k}\) converges to within \(\epsilon ^* + {{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^*\) of both \(\delta \) and the lower bound limit \(\delta ^{L,*}\). It remains to show that the upper bounds that are actually calculated, \(\delta ^{U,k}\), also converge within a reasonable value.
To this end, note that
where \({\bar{\delta }}^{U,k} = {{\,\mathrm{\textstyle {\sum }}\,}}_{i\in I} (g_i(x^k,y_i^k) - g_i^{L,k})\). Combining this with Equation (19), we have \({\bar{\delta }}^{U,k} - {\bar{\delta }}^k = {{\,\mathrm{\textstyle {\sum }}\,}}_i g_i^*(x^k) - g_i^{L,k}\). By construction of \(g_i^{L,k}\), \(0 \le g_i^*(x^k) - g_i^{L,k} \le \eta _i^k\) and so \(0 \le {\bar{\delta }}^{U,k} - {\bar{\delta }}^k \le {{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^k\). It is simple to see that \(\delta ^{U,k} \ge \delta \) for all k, and that it is a non-increasing sequence, and so it must converge to some value greater than \(\delta \):
Further, \(\delta ^{U,k} \le {\bar{\delta }}^{U,k}\) for all k and so \(\delta ^{U,k} - {\bar{\delta }}^k \le {{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^k\). Consequently,
Finally, using this and Inequality (20), if \(\delta ^{U,*}\) is greater than \({\bar{\delta }}^*\), then \(\delta ^{U,*} - \delta ^{L,*} \le \epsilon ^* + 2{{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^*\). Otherwise, we have \(\delta ^{U,*} - \delta ^{L,*} \le \epsilon ^* + {{\,\mathrm{\textstyle {\sum }}\,}}_i \eta _i^*\) (since \(\delta ^{U,*} \ge \delta \)). In either case, we have the conclusion
\(\square \)
C Data for and solution of gas network price equilibrium example
In this section we specify the data used for the example in Sect. 6.3, as well as the equilibrium solution found by the primal-dual approach. The topology of the network is in Fig. 1. See Tables 4, 5, 6 and 7 for the data and solution of the overall nodes, pipelines/transmission, supplies, and demands, respectively. In addition, we have lower and upper bounds on the squared pressure variable \(b_k^p = 900\) (bar\(^2\)) and \(B_k^p = 4900\) (bar\(^2\)), for each node \(k \in K\). Finally, based on the costs of supply and marginal utilities, we enforce the bounds [0, 12.1] for each price \(x_k\) when solving the dual problem. From Table 4, we note that these bounds are not binding at the equilibrium solution.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Harwood, S., Trespalacios, F., Papageorgiou, D. et al. Equilibrium modeling and solution approaches inspired by nonconvex bilevel programming. Comput Optim Appl 87, 641–676 (2024). https://doi.org/10.1007/s10589-023-00524-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00524-w