1 Introduction

In this paper, we present a study at the intersection of machine learning (ML) and operations research (OR). In recent years, significant effort and interest have been put into the flourishing area of using ML to solve OR problems. Although significant results have been achieved, there is still a need for frameworks that can handle the special requirements of various OR problems. Here, we focus on this direction and address OR problems involving uncertainty. We present a framework for solving scenario-based multi-stage stochastic programs by combining learning, heuristics, and mathematical solvers.

The uncertainty is crucial in many OR problems and must be addressed for accurate and realistic representations of systems of interest. Although modeling uncertainty can take many forms, we focus on scenario-based problems, which can be formulated in two or more stages. In general, scenario-based programs are complex to solve. Multi-stage stochastic optimization models are considered to be much harder than two-stage stochastic models. The sequence \(\xi _{t},\) \(t=2,\dots ,T\) is the stochastic process, and the decision made at period t is \(x_{t},\) \(t=1,\dots ,T\). In a multi-stage stochastic program, a decision \(x_{1}\) is taken before the observation of an uncertainty \(\xi _{2}\), but then the decision process repeats itself:

decide(\(x_{1}\)) \(\rightarrow \) observe(\(\xi _{2}\)) \(\rightarrow \) decide(\(x_{2}\)) \(\rightarrow \)... \(\rightarrow \) decide(\(x_{T}\)) \(\rightarrow \) observe(\(\xi _{T}\))

The decision \(x_{t}\) is made in period t and may depend on the data of the process up to and including period t, but not on the future due to the non-anticipativity of the unrealized future uncertainty outcomes. Then the T-stage multi-stage stochastic programs can be expressed as:

$$\begin{aligned} \min _{\begin{array}{c} A_{1}x_{1}=b_{1}\\ x_{1}\ge 0 \end{array} } c_{1}^\intercal x_{1} +\mathbb {E}[\min _{\begin{array}{c} B_{2}x_{1}+A_{2}x_{2}=b_{2}\\ x_{2}\ge 0 \end{array} } c_{2}^\intercal x_{2} +\mathbb {E}[ \dots +\mathbb {E}[ \min _{\begin{array}{c} B_{T}x_{T-1}+A_{T}x_{T}=b_{T}\\ x_{T}\ge 0 \end{array} } c_{T}^\intercal x_{T} ]] ], \end{aligned}$$
(1a)

where \(x_{t} \in \{0,1\}^{n_t}\). The first-stage matrices \(c_{1}\), \(A_{1}\), and \(b_{1}\) are known with sizes of \({n_1} \times 1\), \({m_1} \times {n_1}\), and \({m_1} \times 1\), respectively. For the other stages, \(t=2,\dots ,T\), matrices \(c_{t}\), \(B_{t}\), \(A_{t}\), and \(b_{t}\) have sizes of \({n_t} \times 1\), \({m_t} \times {n_{t-1}}\), \({m_t} \times {n_t}\) and \({m_t} \times 1\), respectively. At stage t, the number of variables is \({n_t} \in \mathbb {Z}^+\), and the number of constraints is \({m_t} \in \mathbb {Z}^+\) for all \(t=1,\dots ,T\). Some or all of these matrices can contain uncertainty.

Multi-stage stochastic programs are very practical in modeling various applications, including airline revenue management (Möller et al., 2008), capacity planning (Huang & Ahmed, 2009), epidemic control planning (Yin & Büyüktahtakın, 2021; Yin et al., 2023b; Yin & Büyüktahtakın, 2022; Yin et al., 2023a), invasive species control and surveillance (Kıbış et al., 2021; Chen et al., 2023), and risk-averse optimization (Homem-de Mello andPagnoncelli, 2016; Bushaj et al., 2022). Despite their modeling power, they pose a computational challenge and usually require specially designed algorithms and heuristics. Exact solution approaches include Lagrangian relaxation (Chen et al., 2002), Dantzig-Wolfe decomposition (Singh et al., 2009), and branch-and-price (Lulli & Sen, 2004).

Most solution algorithms for multi-stage stochastic mixed-integer programs include some form of decomposition or cutting-plane approach, including include Lagrangian relaxation (Chen et al., 2002), Dantzig-Wolfe decomposition (Singh et al., 2009), branch-and-price (Lulli & Sen, 2004), and scenario dominance cuts (Büyüktahtakın, 2022, 2023), and decomposition-based heuristics, such as progressive hedging (Watson & Woodruff, 2011).

In this study, we propose a learning strategy and a testing framework to solve multi-stage stochastic programming problems with binary and continuous variables in a fast setting. Optimization problems are solved repeatedly on a daily basis or more frequently in various areas, including but not limited to logistics (Schmidt & Wilhelm, 2000), energy (Vespucci et al., 2012), healthcare (Guerriero & Guido, 2011), and the air transport industries (Barnhart et al., 2003). Stochastic programs can be used to generate realistic pictures of systems and provide benefits over deterministic problems (Zakaria et al., 2020). However, their size and solution time can limit their benefit. Therefore, problem-specific methods are often required for applications that are frequently solved. This process requires an expert and can be time-consuming. We address this issue and provide a general learning framework for solving scenario-based multi-stage stochastic programs, particularly those that entail making similar decisions over a specified time horizon.

Furthermore, multi-stage stochastic problems require the property of non-anticipativity. Simply put, it ensures that we cannot use information from future periods and the implementability of solutions. The non-anticipativity constraints are fundamental for multi-stage stochastic problems, and they can grow rapidly with the number of scenarios. The underlying stochastic process can be represented with scenarios with a finite number of realizations. The framework that we are proposing is specifically designed to handle scenario-based multi-stage problems and non-anticipativity requirements. We propose a new type of neural network: Non-anticipative Encoder-Decoder with Attention or NEDA, where the Encoder-Decoder with Attention part of the algorithm is based on the neural translation architecture of Luong et al. (2022) and cutting-edge solution algorithms such as stochastic dual dynamic integer programming and progressive hedging and heuristics such as relax-and-fix and adaptive fixing. The details of these baselines used to compare our approach are described in Sect. 5.2.

As an innovative feature of this study, we address the challenge of non-anticipativity with a new neural architecture called NEDA that is specifically designed to solve scenario-based multi-stage stochastic programs. A training mechanism based on deterministic instances, rather than stochastic programs, is presented to significantly reduce training data generation time. Additionally, a novel framework, ScenPredOpt, is presented to utilize predictions from the proposed NEDA neural network. ScenPredOpt integrates a heuristic based on LP relaxation to further improve solution time reductions. Moreover, we propose a variance-based item-wise generalization algorithm that considers the variability of the predictions and extends the predictions to instances with a larger number of items. Our goal is to reduce the solution times of multi-stage stochastic programming problems where they are solved repeatedly, such as vehicle routing, electric power systems, and airline crew planning. Our motivation is to develop a general framework that can solve those problems without a problem-specific design and generate fast and close-to-optimal solutions to multi-stage stochastic programs with many scenarios, periods, and varying dimensions.

2 Literature review

In recent years, the field of machine learning (ML) for solving OR has drawn significant attention. For an excellent review on this subject, we refer to Bengio et al. (2021). Specifically, using ML for solving scenario-based two-stage stochastic programs has gained traction. The closest study to ours is presented by Fre**ger and Larsen (2019). They utilize a learning framework based on a neural translation architecture to solve two-stage stochastic programs. Even though they share the same motivation as ours, i.e., reducing the solution times of stochastic programs, their methodology is significantly different. While we present a new neural architecture that can handle non-anticipativity for multi-stage problems, Fre**ger and Larsen (2019) do not consider the non-anticipativity aspect of the two-stage problem. Fre**ger and Larsen (2019) present a training paradigm based on fully solved stochastic problems, while we present a training strategy based on deterministic and easy-to-solve instances. In addition, Fre**ger and Larsen (2019) ensure the feasibility of predictions using a probability mask, but we present an iterative methodology to select a prediction level that eliminates infeasibility. Additionally, while they predict an averaged solution description for the recourse decision, we output the fully detailed solution for all stages and scenarios of the problem. In a similar vein, Larsen et al. (2022b) present a framework to solve two-stage stochastic programs. The authors work on a problem in which the solution for the second stage is computationally demanding. Therefore, they predict a higher-level and less detailed solution description instead of predicting fully detailed second-stage decisions using multilayer perceptrons.

Abbasi et al. (2020) present a methodology to solve stochastic optimization problems in two stages using well-known machine learning algorithms and a case study on blood transshipment problems with uncertain demand. Abbasi et al. (2020) train their models on the solutions of fully solved stochastic problems and predict only the first-stage decision variables. The first-stage variables are directly actionable; the second-stage variables appear to handle uncertainty and are not actionable. They use classical ML algorithms such as classification and regression trees, k-nearest neighbors, random forest, and neural networks. In practice, the solution framework outperforms the existing policy, but has an optimality gap of 14%. Wu et al. (2021) utilize a conditional variational auto-encoder to solve graph-based two-stage stochastic optimization problems. An encoder is used to generate low-dimensional representations of scenarios, which can be used through a decoder for tasks like scenario reduction and objective prediction. The presented methodology can be used for larger problems and more scenarios than the ones they are trained with. In Crespo-Vazquez et al. (2018), a methodology based on ML is presented to solve the participation problem of wind and storage power plants defined as a two-stage stochastic programming model. They utilize multivariate clustering to generate a set of scenarios from historical data, and the probabilities of scenarios are calculated by a trained Long-Short-Term Memory (LSTM) model. Bengio et al. (2020) present a framework to solve two-stage stochastic programs by predicting a representative scenario of all uncertainty. Therefore, the problem can be solved with a representative scenario deterministically instead of all scenarios and achieve the same solution faster than the Gurobi solver. Also, by only generating a surrogate problem, first-stage feasibility is ensured since the surrogate problem is solved with Gurobi in their framework.

Zheng et al. (2021) propose an encoder-decoder-based framework to solve the online route planning problem that is formulated as a two-stage stochastic program. For supervised learning, the labels are generated by a heuristic algorithm, and probability masking is applied to ensure feasibility. Dumouchelle et al. (2022) utilize neural networks to solve two-stage problems by estimating the expected second-stage cost, which can be done in two ways. In the single-cut version, the expected cost is predicted for a set of scenarios, and in the multi-cut version, the expected cost is predicted for a single scenario. Then, those estimations from the neural network are used in an approximate formulation containing the first-stage decisions. The resulting framework can be used to solve large problems in seconds. Larsen et al. (2022a) present a study to solve two-stage programs using ML to speed up difficult-to-solve second-stage problems. They propose to use multilayer perceptrons and predict the value of the target function when performing the well-known L-shaped method.

In a recent study, Nair et al. (2020) present a learning framework to enhance mixed-integer programming (MIP) solvers using two neural networks. One network is trained to perform multiple partial assignments for its integer variables, which generates smaller sub-problems that can be paralleled. The model is trained using feasible solutions instead of optimal solutions. Another network is trained for variable selection during the branch-and-bound algorithm to generate a bound for the objective function value with a smaller tree. Shen et al. (2021) present a new methodology to enhance branch-and-bound algorithms using ML. In the first step, a graph convolutional network is trained using optimal solutions to problems that can be expressed as graphs. Then, for testing, the trained model outputs a value for each decision variable that represents the probability of being in the optimal solution. In the next step, a probabilistic branching technique with a guided depth-first search is proposed to utilize the optimal solutions predicted. Liu et al. (2022) propose a learning framework by predicting the size of the local branching neighborhood. In the first step, the size of the branching is predicted as a regression task using graph neural networks. In the second stage, the predicted size is dynamically adapted within the local branching algorithms using a trained reinforcement learning model. The results show that the size parameter can be learned, resulting in significant performance gains.

Yilmaz and Büyüktahtakın (2023a) present a deep-reinforcement learning framework to solve stochastic programs based on a two-stage scenario. The authors utilize two different agents for each stage of the problem and can generate solutions for hard problems in a fraction of a second. Bushaj and Büyüktahtakın (2024) present a novel 2-D Deep Reinforcement Learning (DRL) framework that is supported by K-means where the agent, mimicking robot movements, assigns a value of 1 or 0 to each of the variables for the multi-dimensional knapsack problem. Bushaj et al. (2023) integrate an agent-based simulation with a DRL framework for epidemic intervention planning where a governor DRL agent can enforce interventions in the agent-based simulation environment.

Ding et al. (2020) present a study at the intersection of ML and OR. In their framework, a graph convolutional network is trained to predict values of binary decision variables. Then those predictions can either be used to generate a heuristic prediction with a local branching type cut or result in an exact solution with a root branching rule. In a recent study, Jiménez-Cordero et al. (2022) present a methodology for constraint generation that is used to warm-start the solution process. They train an ML model to predict invariant constraints, which is the set of constraints that cannot be removed from the integer programs without changing the feasible region. Shen et al. (2022) aim to improve the solution time of large-scale optimization problems by presenting an ML-based pricing heuristic for the column generation algorithm. The ML model is trained using optimal solutions to the pricing problem in the column generation algorithm, which is the bottleneck of the algorithm. When you have an ML model that predicts the optimal solution to the pricing problem, the efficiency of the branch-and-price increases significantly, which is an exact method.

In Kotary et al. (2021), the authors are interested in learning the OR solution using ML when there are multiple optimal solutions. Additionally, as a result of randomization within combinatorial optimization techniques, the learning task may face a challenge. To overcome this, the problem of optimal dataset design is introduced with a heuristic to find solutions with the smallest total variation. Paulus et al. (2021) present a framework in which integer programming solvers are integrated into neural network architectures as layers that can be learned. The main idea is to provide gradients for both the cost terms and the constraints of an integer program. Therefore, the proposed model can learn the cost and constraints of the problem without explicitly specifying it. Huang et al. (2022) suggest a methodology to rank cuts in a cutting plane algorithm since a good set of cuts can significantly reduce the solution time. The main idea is to learn a scoring function that can measure the efficiency of the cuts and that can be generalized to other instances. The proposed framework can be used during branch-and-cut algorithms with a solver.

Recently, Dai et al. (2021) have introduced Neural Stochastic Dual Dynamic Programming (v-SDDP) to combat high-dimensional and long-horizon stochastic dynamic programs that can be hard to solve with Stochastic Dual Dynamic Programming (SDDP). They utilize a neural network to predict a high-quality value function to increase the efficiency of the SDDP solution. Their study has a similar flavor to ours in terms of its high-level objective, i.e. using ML to help solve sequential stochastic optimization problems. However, they focus on stochastic dynamic programs rather than multi-stage stochastic programs and their solution methodology is entirely different from ours.

2.1 Key contributions of the study

An extensive amount of interest has recently been put toward learning to solve optimization problems; however, there is still a lack of research for solving scenario-based multi-stage stochastic programs. Specifically, deep learning-based supervised methodologies can be considered to solve challenges of training, feasibility, and non-anticipativity in multi-stage stochastic programs. Our motivation is two-fold. First, recent advances at the intersection of machine learning and mathematical optimization programs show a promising direction in solving combinatorial optimization problems (Liu et al., 2022; Larsen et al., 2022b). Second, the vast-applicability and computational difficulties of scenario-based multi-stage stochastic programs inspire us to tackle the computational complexity of the problem. Our goal is to significantly enhance learning-optimization solution algorithms for scenario-based multi-stage stochastic programs by presenting a general framework. Our contributions are summarized below.

To the best of our knowledge, this is the first study that utilizes an encoder-decoder model to learn the solutions of multi-stage stochastic programs. We present an innovative attention-based encoder-decoder model called NEDA, in which the hidden states of the models are adjusted based on the scenario tree to ensure the non-anticipativity of the predicted decision variables. We propose a novel training paradigm for NEDA based on deterministic instances and scenario sampling. This strategy prevents solving stochastic optimization problems to generate training labels, which is computationally intractable.

We introduce the ScenPredOpt framework to handle multi-stage programs by utilizing a general LP-based heuristic to speed up the solution. The ScenPredOpt framework is designed to handle general scenario-based multi-stage programs with binary variables by integrating decisions made by learning models, heuristics, and commercial solvers. Moreover, we improve the item-wise generalization algorithm to account for the variability of the prediction in predicting problems with a large number of items. We test the success of the ScenPredOpt algorithm with a varying number of periods, items, and scenarios. The results show that it outperforms heuristics and that the solution time can be improved by a factor of 599 with a gap of only 0.08%.

Our ScenPredOpt framework provides significant novelty over the PredOpt presented in Yilmaz and Büyüktahtakın (2024) including but not limited to LP relaxation. ScenPredOpt outlines a general methodology to solve scenario-based multi-stage stochastic MIPs, where PredOpt focuses on multi-period deterministic MIP problems. Multi-stage stochastic programming presents quite different challenges and, therefore, requires novel methodologies. First, the ScenPredOpt framework involves a novel ML framework, namely the NEDA network, which generates predictions that meet the non-anticipativity requirement of the multi-stage stochastic programs while PredOpt fails to satisfy this property. Furthermore, we extend the item-wise generalization algorithm with a variance-based strategy and compare it with PredOpt.

Section 3 presents the formulation of SMCLSP and SMSMK and a brief review discussion of the traditional solution approaches. Section 4 outlines the details of NEDA, scenario sampling-based training, ScenPredOpt framework, and item-wise generalization algorithm. Then in Sect. 5, implementation details, including instance generation, training, and evaluation, are presented. Section 6 demonstrates the computational results along with generalization experiments. Finally, Sect. 7 concludes the study with suggestions for future directions.

3 Problems

3.1 Stochastic multi-item capacitated lot-sizing problem

Lot-sizing applications have been central for many industries, including but not limited to glass, chemical, pharmaceutical, steel, paper, and manufacturing. The lot size problem has many variations, including setup times, multiple machines, cyclical schedules, and perishable inventories (Jans & Degraeve, 2008). In this study, we present a scenario-based version of the classical MCLSP. Here, some or all parameters of the problem can be uncertain and can be represented with scenarios. The objective is to minimize the total cost of production, setup, and inventory costs while satisfying the demand for each item under all scenarios. Therefore, MCLSP and SMCLSP are NP-Hard (Bitran & Yanasse, 1982).

SMCLSP can be expressed as an MIP, with the number of periods T, items I, and scenarios S. The parameters of the problems are assumed to be non-negative and are as follows: production cost \(p_{it}^{s}\), setup cost \(f_{it}^{s}\), inventory cost per unit \(h_{it}^{s}\), demand \(d_{it}^{s}\), and capacity \(c_{t}^{s}\) \(\forall i\in \left\{ 1,\ldots ,I\right\} ,\hspace{5.0pt}\forall t\in \left\{ 1,\ldots ,T\right\} ,\hspace{5.0pt}\forall s\in \left\{ 1,\ldots ,S\right\} \). The probability of each scenario is represented by \(\omega ^{s}\). The set of scenarios that share the same scenario path with scenario s up to and including period t for item i is represented by \(\Psi _{it}^{s}\). Non-negative continuous variables \(x_{it}^{s}\) and \(v_{it}^{s}\) represent the units produced and inventory at the end of each period, respectively. The binary variable \(y_{it}^{s}\) takes the value 1 if the item i is produced in period t for scenario s, and 0 if not. The SMCLSP formulation:

$$\begin{aligned} \min{} & {} \sum _{s=1}^{S} \omega ^{s} \sum _{i=1}^{I} \sum _{t=1}^{T} (p_{it}^{s}x_{it}^{s} + f_{it}^{s}y_{it}^{s} + h_{it}^{s}v_{it}^{s}) \end{aligned}$$
(2a)
$$\begin{aligned} \text {s.t.}{} & {} v_{i,t-1}^{s} + x_{it}^{s} - d_{it}^{s} = v_{it}^{s} \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(2b)
$$\begin{aligned}{} & {} \sum _{i=1}^{I} x_{it}^{s} \le c_{t}^{s} \quad \forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(2c)
$$\begin{aligned}{} & {} x_{it}^{s} \le y_{it}^{s}c_{t}^{s} \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(2d)
$$\begin{aligned}{} & {} x_{it}^{s} =x_{it}^{s^\prime } \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S, \hspace{5.0pt}s^\prime \in \Psi _{it}^{s} \end{aligned}$$
(2e)
$$\begin{aligned}{} & {} y_{it}^{s} =y_{it}^{s^\prime } \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S, \hspace{5.0pt}s^\prime \in \Psi _{it}^{s} \end{aligned}$$
(2f)
$$\begin{aligned}{} & {} v_{it}^{s} =v_{it}^{s^\prime } \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S, \hspace{5.0pt}s^\prime \in \Psi _{it}^{s} \end{aligned}$$
(2g)
$$\begin{aligned}{} & {} x_{it}^{s},v_{it}^{s} \ge 0 \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T, \hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(2h)
$$\begin{aligned}{} & {} y_{it}^{s} \in \{0,1\} \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S. \end{aligned}$$
(2i)

The objective function (2a) minimizes the expected cost of production, setup, and inventory in all scenarios, items, and periods. Constraints (2b) assure the flux of inventory in a periodic setting, while demand is satisfied for each item i. Constraints (2c) limit the amount produced for each item by a shared capacity for all items, and constraints (2d) administer the setup cost for the item i produced in period t. Constraints (2e), (2f), and (2g) are non-anticipativity constraints for \(x_{it}^{s}\), \(y_{it}^{s}\), and \(v_{it}^{s}\), respectively. Then constraints (2h) establish the nonnegativity of \(x_{it}^{s}\) and \(v_{it}^{s}\). Finally, the constraints (2i) put binary restrictions on \(y_{it}^{s}\).

The variants of the lot-sizing problem include uncertain demand (Brandimarte, 2006), biofuel production (Kantas et al., 2015), and carbon emissions (Benjaafar et al., 2012). Lot-sizing solution approaches have been studied extensively in the literature. Notably, an exact solution framework was presented by Florian et al. (1980). Furthermore, another important exact approach with valid (\(\ell \),S) inequalities and a separation algorithm was introduced by Barany et al. (1984). More recently, Büyüktahtakın et al. (2018) present dynamic programming-based inequalities to improve the solution of the multi-item capacitated lot-sizing problem. Büyüktahtakın and Liu (2016) present a study on solving single-item capacitated lot-sizing problem by combining dynamic programming with data fitting and approximation. We refer to Pochet and Wolsey (2006) for a review of algorithms on lot-sizing. For general information on stochastic lot-sizing problems, we refer to the review by Tempelmeier (2013). Stochastic lot-sizing problems can be much more challenging, and thus solution approaches such as dynamic programming (Huang & Küçükyavuz, 2008) and progressive hedging (Haugen et al., 2001) are used. Also, more general approaches that are specifically developed to solve multi-stage scenario-based programs can be utilized to solve SMCLSP. One of the most recent and highly successful approaches has been developed by Zou et al. (2019). Their developed stochastic dual dynamic integer programming (SDDiP) framework utilizes different types of cutting planes and achieves a state-of-the-art solution framework for solving multi-stage stochastic programs in different settings (Lara et al., 2020; Yu & Shen, 2020). In another recent study, Büyüktahtakın (2023) proposes scenario dominance cutting planes to solve SMCLSP quickly and with high quality. Heuristic approaches based on the relax-and-fix approach are highly used to solve both deterministic and stochastic versions of the MCLSP (Helber & Sahling, 2010; Toledo et al., 2015; Absi & van den Heuvel, 2019; Beraldi et al., 2006).

3.2 Stochastic multi-stage multi-dimensional knapsack problem

The stochastic multi-stage multi-dimensional knapsack problem is a periodical version of the well-known knapsack problem that also includes uncertainty. In this setting, the aim is to maintain a stable solution over time by maximizing the profit and the stabilization bonus while ensuring that capacity constraints are not violated. Even in a single-dimensional setting, the problem is NP-Hard (Bampis et al., 2022). The consideration of stability over time plays a vital role in applications such as periodically changing prices, energy, raw materials, and resources.

SMSMK is formulated as a binary integer program for a number of periods T, items I, and scenarios S. The binary variable \(x_{it}^{s}\) denotes the decision to insert the item \(i \in \left\{ 1,\ldots ,I\right\} \), in period \(t \in \left\{ 1,\ldots ,T \right\} \), in scenario \(s \in \left\{ 1,\ldots ,S \right\} \) by taking a value of 1, and 0 otherwise. The binary variable \(y_{it}^{s}\) is introduced as the stabilization bonus and assigned a value of 1 if the decision in period t and \(t+1\) is identical, that is, \(x_{it}^{s}, x_{i,t+1}^{s}=0\), or \(x_{it}^{s}, x_{i,t+1}^{s}=1\). Otherwise, \(y_{it}^{s}\) takes the value 0. For item i, period t and scenario s the profit is denoted by \(p_{it}^{s}\), and the bonus is denoted by \(b_{it}^{s}\) except for \(t \ne T\) since \(T-1\) is the last period the stability bonus is added. The problem considers J different knapsack constraints, and the weights are denoted by \(w_{ijt}^{s}\) for each item \(i \in \left\{ 1,\ldots ,I\right\} \), knapsack constraint \(j \in \left\{ 1,\ldots ,J \right\} \), period \(t \in \left\{ 1,\ldots ,T \right\} \), and scenario \(s \in \left\{ 1,\ldots ,S \right\} \). For each resource constraint, the capacity of the knapsack is indicated by \(c_{jt}^{s}\). \(\Psi _{it}^{s}\) is the set of scenario indexes that share the same path with scenario s up to and including period t for item i. In addition, \(\omega ^{s} \) is the probability of each scenario. We modify the formulation in Bampis et al. (2022) to include scenarios and present the problem as:

$$\begin{aligned} \max{} & {} \sum _{s=1}^{S} \omega ^{s} (\sum _{i=1}^{I} \sum _{t=1}^{T} p_{it}^{s}x_{it}^{s} + \sum _{i=1}^{I} \sum _{t=1}^{T-1} b_{it}^{s}y_{it}^{s})\end{aligned}$$
(3a)
$$\begin{aligned} \text {s.t.}{} & {} \sum _{i=1}^{I} w_{ijt}^{s}x_{it}^{s} \le c_{jt}^{s} \quad \ \forall t=1,\ldots ,T,\hspace{5.0pt}\forall j=1,\ldots ,J,\hspace{5.0pt}\forall s=1,\ldots ,S \nonumber \\ \end{aligned}$$
(3b)
$$\begin{aligned}{} & {} y_{it}^{s} \le -x_{i,t+1}^{s} + x_{it}^{s}+1 \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T-1,\hspace{5.0pt}\forall s=1,\ldots ,S \nonumber \\ \end{aligned}$$
(3c)
$$\begin{aligned}{} & {} y_{it}^{s} \le x_{i,t+1}^{s} - x_{it}^{s} +1 \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T-1,\hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(3d)
$$\begin{aligned}{} & {} x_{it}^{s} =x_{it}^{s^\prime } \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S, \hspace{5.0pt}s^\prime \in \Psi _{it}^{s} \end{aligned}$$
(3e)
$$\begin{aligned}{} & {} y_{it}^{s} =y_{it}^{s^\prime } \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T-1,\hspace{5.0pt}\forall s=1,\ldots ,S, \hspace{5.0pt}s^\prime \in \Psi _{it}^{s} \end{aligned}$$
(3f)
$$\begin{aligned}{} & {} x_{it}^{s} \in \{0,1\} \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T,\hspace{5.0pt}\forall s=1,\ldots ,S \end{aligned}$$
(3g)
$$\begin{aligned}{} & {} y_{it}^{s} \in \{0,1\} \quad \forall i=1,\ldots ,I,\hspace{5.0pt}\forall t=1,\ldots ,T-1,\hspace{5.0pt}\forall s=1,\ldots ,S. \end{aligned}$$
(3h)

The objective function (3a) maximizes the expected profit and stability bonus over all scenarios. Constraints (3b) are knapsack constraints that limit the weights of selected items by capacity. The following constraints (3c) and (3d) secure the enforcement of the bonus if \(x_{it}=x_{i,t+1}\). Precisely, they represent the linear equivalent of \(y_{it}^{s} =1- |x_{i,t+1}^{s} - x_{it}^{s}|\). Constraints (3e) and (3f) ensure the non-anticipativity for \(x_{it}^{s}\) and \(y_{it}^{s}\), respectively. Finally, binary restrictions for \(x_{it}^{s}\) and \(y_{it}^{s}\) are given in constraints (3g) and (3h).

The knapsack problem has been studied extensively in the OR literature in various forms. The knapsack problem has a wide range of applications, and many types of complex OR problems can be expressed as knapsack-type sub-problems (Varnamkhasti, 2012). Examples include multiple objectives (Ishibuchi et al., 2014), online knapsack (Cygan et al., 2016), stochastic knapsack (Kosuch & Lisser, 2011), and probabilistic constraints (Gaivoronski et al., 2011). Numerous exact and heuristic approaches have been developed to solve different versions of the knapsack problem. We refer to Cacchiani et al. (2022) for a discussion of recent advances in knapsack problems. As there are not many solution approaches specially developed for SMSMK (3a)-(3h), we utilize a well-known solution framework, namely progressive hedging (PH), for scenario-based multi-stage problems. Introduced by Rockafellar and Wets (1991), PH uses the idea of relaxing non-anticipativity constraints and solves sub-problems independently. Later, a punishment for violating non-anticipativity is added to the objective for each sub-problem. PH performs well in various stochastic integer problems (Gul et al., 2015; Veliz et al., 2015). Büyüktahtakın (2022) presents the scenario dominance concept and a new scenario sub-problem that respects the non-anticipativity constraints to derive bounding relations between scenario couples and solve the multi-stage stochastic knapsack problem.

4 Methodology

Our methodology innovatively integrates deep learning with heuristics and optimization solvers to find efficient solutions to multi-stage stochastic optimization problems. The deep learning aspect of our methodology utilizes neural machine translation frameworks to predict solutions that are close to optimal. This is achieved by learning a map** from input defined by the problem parameters to an output defined by solver-generated optimal solutions. The details of the neural machine translation for the multi-stage stochastic programs and non-anticipative encoder-decoder with attention (NEDA) are given in Sect. 4.1. Then, in Sect. 4.2, we introduce the ScenPredOpt framework that combines learning-based decision making, heuristics, and mathematical optimization solvers, achieving remarkable reductions in solution time, as demonstrated in Sect. 6.

4.1 Non-anticipative encoder-decoder with attention

4.1.1 Neural machine translation and the requirements for multi-stage non-anticipativity

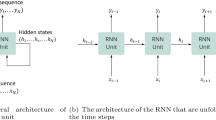
A machine translation system is used to translate from one language to another. In recent years, neural network-based translation systems have gained significant attention and achieved remarkable results (Stahlberg, 2020). In such systems, the sequence \(x_{1},x_{2}, \ldots ,x_{m}\) is the input of the source language and is translated into the target language by generating the output sequence \(y_{1},y_{2}, \ldots ,y_{n}\). The neural machine translation model is trained using pairs of input and output sequence pairs by maximizing the conditional probability: \(P (y \mid x) = \prod _{t=1}^{n} P (y_{t} \mid y_{i \mid i < t},x)\). The readers can refer to Stahlberg (2020) for a detailed review of neural machine translation systems. We develop our NEDA based on the architecture presented by Luong et al. (1b. The decision variables should take the same value if they share the same realizations of the scenarios up to the node’s stage, which is also known as time consistency. For example, all decisions for scenario one should be identical; therefore, there is only one scenario group. In stage two, there are two scenario groups: The upper group for scenarios one to four and the lower group for scenarios five to eight.

The learning network can generate predictions using the data in tabular and extended formats, as presented in Fig. 1b. However, this raises a critical complication for the problem of interest with non-anticipativity. This is because the attention-based neural network uses the processed input information from the preceding and subsequent periods. The former case is harmless since the information from the preceding periods is the same for all scenarios that have the same parent node. However, for the succeeding periods, the child nodes will have different parameters to represent changing scenario data. In effect, the original input data and, therefore, the processed input data are likely to be different for each distinct child node. Since those generated hidden states will be used within the attention mechanism, the predictions can end up being different for each scenario group that requires non-anticipativity. This would lead to a violation of the non-anticipative structure of the problem and would result in an unimplementable decision. For example, we can consider predicting the first scenario group consisting of scenarios one to four in the second stage. The parameters and, therefore, the input data for the first stage would be the same for scenarios one to four. On the other hand, when we are at stage three, only scenarios one and two are identical.

Similarly, scenarios three and four are identical, considering only stage three. Assuming that the attention-based learning model decides by only considering the preceding and succeeding periods, i.e., the attention window of size one, the predictions made would be the same for scenarios one and two and the same for scenarios three and four at stage three. These two sets of predictions would probably be different from each other at stage three, since the encoder uses fourth-stage data when predicting. This would violate the fundamental non-anticipativity requirement. In this small example, if the size of the attention window is two, then four different predictions can be made for the first scenario group, that is, scenarios one to four of the second stage. The learner network makes use of input data for the fourth period and the third period, which would have different parameters for child nodes. Having this violating condition makes the predictions for the scenario-based multi-stage stochastic program infeasible and inexecutable. In order to eliminate this violation, we propose a novel neural network architecture called Non-anticipative Encoder-Decoder with Attention or NEDA.

4.1.2 NEDA framework

The proposed NEDA model is based on the network presented by Luong et al. (2015) and modified to handle the non-anticipative nature of the issue of interest. The main idea is to generate the same encoder hidden state information for all succeeding periods that share the same parent node. Building on previous example, in Fig. 1b, we can consider generating a second-stage prediction for the first scenario group consisting of scenarios 1 to 4. To generate a prediction that ensures non-anticipativity, the hidden states on the next periods within the attention windows should be the same. This is accomplished by averaging the encoder hidden states of child nodes. Here, the hidden states of scenarios 1 to 8 of the first stage and the scenarios 1 to 4 of the third stage have been averaged separately to generate predictions using an attention window of one. The alignment for averaging operations depends on the structure of the scenario tree and is performed separately for each stage and scenario group when generating predictions. When generating the second stage prediction for the second scenario group consisting of scenarios five to eight, the hidden states of scenarios 1 to 8 of the first stage and those of 5 to 8 of the third stage have been averaged separately. The encoder processes all input sequences at once and generates the hidden states, which ideally capture the characteristics and features of the problem parameters. The forward encoder layer \(LSTM^{e}_{f}\) generates the hidden state \(\overrightarrow{h}^{e}_{t,s}\) and the backward encoder layer \(LSTM^{e}_{b}\) generates the hidden state \(\overleftarrow{h}^{e}_{t,s}\). Given the current period t and the length of the attention window D, we can represent the hidden state generated for each scenario \(s\in \left\{ 1,\ldots , S\right\} \) as:

$$\begin{aligned} \overrightarrow{h}^{e}_{t-D,s},\ldots ,\overrightarrow{h}^{e}_{t,s},\ldots ,\overrightarrow{h}^{e}_{t+D,s} = LSTM^{e}_{f}(x_{t-D,s},\ldots ,x_{t,s}, \ldots ,x_{t+D,s}), \end{aligned}$$
(4a)
$$\begin{aligned} \overleftarrow{h}^{e}_{t-D,s},\ldots ,\overleftarrow{h}^{e}_{t,s},\ldots ,\overleftarrow{h}^{e}_{t+D,s} = LSTM^{e}_{b}(x_{t-D,s},\ldots ,x_{t,s}, \ldots ,x_{t+D,s}). \end{aligned}$$
(4b)

The hidden states of the forward and backward LSTM layers within the attention window are concatenated and represented as a single encoder hidden state \(h^{e}_{t,s}=[\overrightarrow{h}^{e}_{t,s},\overleftarrow{h}^{e}_{t,s}] \hspace{5.0pt}\forall t \in \) \(\left\{ t-D,\ldots ,t,\ldots , t+D\right\} \hspace{5.0pt}\forall s \in \) \(\left\{ 1,\ldots ,S\right\} \). Let \(\Omega _{t,s}\) denote the indices of scenarios that share the same scenario realization up to the current period t with scenarios s. Therefore, for each scenario s in the problem, averaged hidden states \(h^{e}_{t,s} \) can be calculated as:

$$\begin{aligned} h^{e}_{t,s} = {\sum _{s \in \Omega _{t,s} } h^{e}_{t,s} \over |\Omega _{t,s} |}. \end{aligned}$$
(5)

The explanation behind the the averaging step is to determine all groups of scenarios that have a hidden state similar to the current prediction period t. If those hidden states are close to each other, then the averages of the hidden states would be close to each other. In the end, the model would make a similar prediction of binary variables. However, if the hidden states vary from each other, the trained NEDA model would get varying hidden states throughout the periods. Therefore, the attention scores and context calculated in succeeding steps would lead to differently predicted binary variables for the same scenario clusters violating non-anticipativity. To prevent that, the NEDA model would make an unsure prediction using the averaged hidden states, and the determination of those decision variables would be left to the ScenPredOpt framework, therefore, to the commercial solver to find the best obtainable values.

The decoder cell state is initialized as the scenario average and produces the output sequence. The decoder \(LSTM^{d}\) also generates the decoder hidden state \(h^{d}_{t,s}\) for the current period t using the decision made in the previous period:

$$\begin{aligned} h^{d}_{t,s} = LSTM^{d}(y_{t-1,s}), \end{aligned}$$
(6)

Then the attention module is used to further incorporate averaged encoder hidden state \(h^{e}_{i,s}\) by making a comparison with the current decoder hidden state \(h^{d}_{t,s}\). The attention score \(a_{i,s}\) is calculated as:

$$\begin{aligned} a_{i,s}=\frac{exp(score(h^{d}_{t,s},h^{e}_{i,s}))}{\sum _{t^{\prime }=t-D}^{t+D} exp(score(h^{d}_{t,s},h^{e}_{t^{\prime },s}))} \quad \forall i \in \left\{ t-D,\ldots , t+D\right\} , \hspace{5.0pt}\forall s \in \left\{ 1,\ldots ,S\right\} , \end{aligned}$$
(7)

and the score is calculated by the following formula:

$$\begin{aligned} score(h^{d}_{t,s},h^{e}_{i,s})={h^{d}_{t,s}}^\intercal W_{\alpha } h^{e}_{i,s} \quad \forall i \in \left\{ t-D,\ldots , t+D\right\} . \end{aligned}$$
(8)

Using the attention scores, a weighted average of encoder hidden states is taken to calculate the context:

$$\begin{aligned} cn_{t,s} = \sum _{i=t-D}^{t+D} a_{i,s} \times h^{e}_{i,s}. \end{aligned}$$
(9)

Finally, context \(cn_{t,s}\) is concatenated with the decoder hidden state and passed through a linear layer to generate a prediction for scenario s in period t. Note that for all scenarios that share the same scenario realization up to period t, the predicted values would be the same since the predictions are calculated from the same averaged hidden states calculated with Eq. (5).

4.2 The ScenPredOpt framework

4.2.1 Training and scenario sampling

In the ScenPredOpt framework, the learner is responsible for decisions in all periods over all scenario paths that are linked with non-anticipativity constraints, as ensured by the NEDA framework.

One major challenge for solving scenario-based multi-stage stochastic programs is the generation of training instances. The encoder-decoder models require a significant amount of training data generated by a commercial solver in the order of millions to learn the optimal solutions. Therefore, this instance generation approach would be unsuitable for scenario-based multi-stage stochastic programs, even for short-period instances, as they are much more complex and significantly harder to solve than deterministic multi-stage problems. To overcome this computation challenge, we propose a training strategy based on scenario sampling. In this strategy, at each training epoch, we sample a single scenario for each instance and perform a training step using that scenario data and its optimal solution.

Our proposed training based on scenario sampling achieves a few computational advantages. First, considering that the model is trained by the optimal solutions of 3,500,000 instances, it can be computationally infeasible to solve many multi-stage stochastic problems with multiple scenarios. However, solving the problem with only a single scenario, i.e., a single scenario path in Fig. 1b, only takes a few seconds with the Gurobi solver. In this setting, the non-anticipativity constraints in the formulation are removed, and therefore, each subproblem of scenarios can be solved independently in a fast manner. Second, by sampling a problem with a single scenario path, we increase the learning efficiency in a manner similar to experience replay (Mnih et al., 1a, all parameters of the fourth stage scenario would be the same if the cap** period is set to three. Otherwise, the parameters for scenarios 1,3,5, and 7 would be identical and the parameters for scenarios 2,4,6, and 8 would be identical. In Appendix A, we present further details of the generated test instances.

SMCLSP Instances: Instance generation for SMCLSP is implemented according to the approach given in Büyüktahtakın et al. (2018). The hardness of the SMCLSP is controlled by two main factors: capacity-to-demand ratios \(c \in \left\{ 10,14\right\} \) and setup-to-holding cost ratio \(r=1,000\). The production cost \(p_{it}^s\) is drawn from \(U\left[ 1,200\right] \), the inventory cost \(h_{it}^s\) is sampled from \(U\left[ 1,100\right] \), and the demand \(d_{it}^s\) is drawn from \(U\left[ 500,1500\right] \). The overall means of d and h are represented by \(\bar{d}\) and \(\bar{h}\), respectively. Capacity \(c_{t}\) is drawn from \(U\left[ 0.8c\bar{d},1.2c\bar{d}\right] \) and setup cost \(f_{it}^s\) is drawn from \(U\left[ 0.9r\bar{h},1.1r\bar{h}\right] \). Two different models are trained for SMCLSP: The first model is trained with \(T=40\) periods and \(I=8\) items. The second model is trained with \(T=30\) periods and \(I=12\) items. For both models, data sets with some combinations of \(T \in \left\{ 10,15\right\} \) and \(S \in \left\{ 32,64,81,125,243,512\right\} \), where S is the number of scenarios, are used for testing. For item-wise expansion, we used \(T \in \left\{ 15,10\right\} \), \(S \in \left\{ 32,64,81\right\} \), and \(I \in \left\{ 24,32,16\right\} \) for the first model with \(I=8\) and \(T \in \left\{ 15,10\right\} \), \(S \in \left\{ 32,64,81\right\} \), and \(I \in \left\{ 36,48,24\right\} \) for the second model with \(I=12\). For SMCLSP, 18 test sets are generated, each including 20 test instances.

SMSMK Instances: Instances are generated similar to Angulo et al. (2016). Profit \(p_{it}^s\) is drawn from \(U\left[ 1,1000\right] \), stability bonus \(b_{it}^s\) is drawn from \(U\left[ 1,1000\right] \), weights of the elements \(w_{ijt}\) are drawn from \(U\left[ 1,1000\right] \), and capacity \(c_{jt}^s\) is drawn from \(U\left[ 0.5\sum _{i=1}^{I}w_{ijt},0.8\sum _{i=1}^{I}w_{ijt}\right] \). Two models are trained for SMSMK: The one with \(T=30\) periods with \(I=8\) items and the second with \(T=30\) periods with \(I=10\) items. The test set for both models has some combination of \(T \in \left\{ 10,15\right\} \) and \(S \in \left\{ 32,64,81,125,243,512\right\} \). For the first model trained with \(I=8\), instances with \(T \in \left\{ 15,10\right\} \), \(S \in \left\{ 32,64,81\right\} \), and \(I \in \left\{ 24,32,16\right\} \) are used to test item-wise expansion. For the second model trained with \(I=10\), the test set with \(T \in \left\{ 15,10\right\} \), \(S \in \left\{ 32,64,81\right\} \), and \(I \in \left\{ 30,40,20\right\} \) are generated with item-wise expansion. A total of 30 test sets, each with 20 instances, have been generated.

5.2 Implementation Specifications

For SMCLSP, we implement SDDiP based on Ding et al. (2019) with a default setting and a time limit of 7200 s until 20 stable iterations are achieved. Additionally, we implement a heuristic based on Absi and van den Heuvel (2019) to generate a baseline for comparison. Within the heuristic, the number of fixed periods is assigned as \(T \over 20\), and the periods with binary variables are assigned as \(T \over 10\). For SMSMK, we utilize the PH approach presented by Watson and Woodruff (2011) to compare the quality of our solution. Their PH algorithm is an enhanced version of the classical PH algorithms that address convergence issues. SDDiP is not applicable for SMSMK, since SDDiP requires the complete or relatively complete recourse condition, and SMSMK is not completely recourse. Additionally, we utilize the heuristic solution presented in Bertsimas and Demir (2002) for the benchmark, as there is no existing heuristic approach specifically developed for SMSMK given by Eq. (3). Their heuristic solves an LP relaxation of the problem at each iteration. Due to the computational challenge of this heuristic, we set 0.1% of binary variables to 0 instead of a single variable at each step of the iteration. This modification results in a much faster heuristic solution at the cost of a slightly increased optimality gap for instances with a very large number of variables. Our objective with this modification is to present a more fair time comparison between ScenPredOpt and the heuristic of Bertsimas and Demir (2002).

We set the initial level for model-predicted binary variables \(\theta _{M}=50\%\) for SMCLSP and \(\theta _{M}=40\%\) for SMSMK. For both problem types, we assign the initial level for the LP relaxation-assigned binary variables \(\theta _{LP}=5\%\). Also, the reduction in the level for the model-predicted binary variables \(\lambda _{M}=10\%\) and the reduction in the level for the LP relaxation-assigned binary variables \(\lambda _{LP}=1\%\). The time to generate predictions is less than one second for all instances and is included in timeScenPredOpt. For all tables, we present the number of stages T and the total number of scenarios sc.

5.3 Model training

The NEDA models are trained with longer period problems than the instances in the test set to capture and learn more sequential decision structures with the attention structure. The instances used in the training set are deterministic and solved in 1.7 s on average. The SMCLSP models in Tables 1 and 2 have 128 and 64 hidden units in the decoder for both the forward and backward layers, respectively. The former SMCLSP model is trained for 18 h using a training set with \(T=40\). The latter SMCLSP model is trained using \(T=30\) problems in 30 h. The SMSMK models with the results presented in Tables 4 and 5 are trained using instances with \(T=30\) and contain 256 and 128 hidden units in both forward and backward layers, respectively. The encoders contain two bidirectional LSTM layers, while the decoder contains a unidirectional 2-layer LSTM. We have utilized a standard learning schema by applying training, validation, and test sets that contain 3,500,000, 10,000, and 20 instances, respectively (Alpaydin, 2020). Furthermore, a dropout schema (Srivastava et al., 2014) is used to regularize learning with a random rate of \(\left\{ 0.25,0.30,0.35\right\} \), which is known to limit overfitting. We use the popular Adam optimizer with an initial learning rate of 0.01 for SMCLSP and 0.001 for SMSMK (Kingma & Ba, 2014).

5.4 Evaluation methodology

We have utilized the following metrics to measure the success of ScenPredOpt solution time and its quality compared to exact and heuristic approaches.

  • timeGRB: Average solution time in CPU seconds for SMCLSP or SMSMK with Gurobi 9.5 in its default settings.

  • timeScenPredOpt: Average solution time in CPU seconds for SMCLSP or SMSMK with the ScenPredOpt framework.

  • timeHeur: Average solution time in CPU seconds for the heuristic of Absi and van den Heuvel (2019) for SMCLSP and the heuristic of Bertsimas and Demir (2002) for SMSMK.

  • timeSDDiP: Average solution time in CPU seconds for SMCLSP with SDDiP.

  • timePH: Average solution time in CPU seconds for SMSMK with the PH algorithm.

  • accScenPredOpt(%): Percentage of correct binary variables predicted and fixed by ScenPredOpt (or accScenPredOptWoLP for ScenPredOpt without LP relaxation) with respect to the Gurobi solution.

In addition, we define the following metrics:

Definition 1

The optimality gap between the ScenPredOpt solution \(\hat{x}^*\) (heuristic solution for optGapHeur, SDDiP solution for optGapSDDiP, and PH solution for optGapPH) and Gurobi solution \(x^*\). Let \({Z}(\bullet )\) be the corresponding operator to calculate the value of the function given any solution. Then the optimality gap is:

$$\begin{aligned} \mathbf {optGapScenPredOpt (\%)} = \frac{\left| {Z}(\hat{x}^*)-{Z}(x^*)\right| }{{Z}(x^*) } \times 100. \end{aligned}$$
(10)

Definition 2

The solution time improvement factor achieved by employing the ScenPredOpt framework (heuristic time improvement for timeImpHeur, SDDiP time improvement for timeImpSDDiP, and PH time improvement for timeImpPH) compared to Gurobi solution time is:

$$\begin{aligned} \textbf{timeImpScenPredOpt} = \frac{timeGRB}{timeScenPredOpt}. \end{aligned}$$
(11)

Definition 3

The one-sided Wilcoxon signed rank test is used to measure if both samples are from the same population. It is a nonparametric alternative to the t test and appropriate for statistically comparing solution times of ML-based OR approaches (Accorsi et al., 2022). We conclude that ScenPredOpt is statistically faster than the heuristic if the p-value is smaller than 0.01. The hypotheses are as follows:

$$\begin{aligned} H_{0}:&median(timeHeur-timeScenPredOpt) < 0,\end{aligned}$$
(12a)
$$\begin{aligned} H_{1}:&median(timeHeur-timeScenPredOpt) > 0. \end{aligned}$$
(12b)

6 Results

This section provides a discussion of computational experiments. We compare the ScenPredOpt framework with the optimization solver, exact, and heuristic approaches. The test set for each specified characteristic of an instance includes 20 test instances, and all the results presented in the tables are average values for those 20 instances. All instances are solved using Gurobi 9.5 with a 2 h time limit (Gurobi Optimization, LLC, 2022).

6.1 Quality of predictions for SMCLSP

Table 1 presents the detailed computational results for the first set of SMCLSP instances. The 8-item model is trained using deterministic instances sampled by scenarios with \(T=40\) periods and 8 items. The local attention structure helps the model to generalize instances with a varying number of periods. In the first set of Table 1, the test has 32 scenarios and \(T=10\) stages. Gurobi achieves an average solution time of more than 3000 s, while SDDiP reduces the solution time to nearly 450 s with a gap of 0.03% to the Gurobi value. The heuristic significantly reduces the solution time to almost 8 s, with a relatively high optimality gap of 2.13%. ScenPredOpt remedies the trade-off between solution time and quality and achieves a 3.6-second solution with only a 0.16% optimality gap. Here, the solution time is reduced by a factor of 600, when compared to Gurobi. For the third set of instances with 81 scenarios, ScenPredOpt achieves a similar solution time improvement with a gap of only 0.08%. The Gurobi solution time of the instances is not necessarily proportional to the number of scenarios or stages; rather, it is likely related to the structure of scenario trees. However, ScenPredOpt can solve the 8-item SMCLSP for all cases much faster than Gurobi, SDDiP, and heuristic. Also, compared to the heuristic, the optimality gaps are much smaller. The p-values for the Wilcoxon signed rank test are all below 0.01, ensuring that ScenPredOpt is faster than the heuristic. The time improvement factor values for ScenPredOpt decrease as problems become more difficult because the solution time is set to a 2-hour time limit. Gurobi would require a much longer solution time than two hours for harder instances, as proved by the increasing optimality gap. Since ScenPredOpt has no solution time set, the solution with ScenPredOpt starts to take a long time, and the time improvement values appear to shrink. The time improvement values would be much higher if the Gurobi benchmark instances did not terminate early on.

Table 1 Average results of experiments for SMCLSP with 8 items
Full size table

Table 2 shows the computational results with 12-item SMCLSP. Here, the model is trained using \(T=30\)-period instances with 12 items. The results show a similar trend to that of Table 1, favoring ScenPredOpt over the heuristic. Gurobi solves the first three sets of instances in Table 2 on an average of more than 6000 s. ScenPredOpt solves all three of those instances in less than a minute, achieving a small optimality gap of less than 0.41%. The SDDiP halves solution time with a small optimality gap, but still does not reach a fast solution like ScenPredOpt. The last three sets of instances are significantly challenging since none of the individual instances can be solved to optimality in the set 2-hour time limit using Gurobi, hence the average Gurobi solution time of approximately 7200 s. For such instances, the heuristic time is close to or more than 1000 s, whereas the ScenPredOpt time is closer to 100 s with a significantly lower optimality gap compared to the heuristic. Also, LP-relaxation provides an accuracy improvement in the ScenPredOpt.

All p-values of the Wilcoxon test are smaller than 0.01, suggesting that ScenPredOpt is faster with a much smaller optimality gap than the heuristic. Therefore, ScenPredOpt achieves a notable computational advance by generating fast, high-quality solutions to challenging scenario-based multi-stage stochastic programs. Also, for Tables 1 and 2, the overall average and median solution time with the ScenPredOpt is smaller than the heuristic solution time with a lower standard deviation. Therefore, we can highlight that ScenPredOpt outperforms the heuristic in the solution.

Table 2 Average results of experiments for SMCLSP with 12 items
Full size table

6.1.1 Comparison of ScenPredOpt and Gurobi in the first few seconds

Figure 3 presents the progress of the normalized objective function values during the first seconds of the solution for ScenPredOpt and Gurobi. Specifically, Fig. 3a and b show the progress of the solution for the third and fifth sets of instances in Table 1, with 81 and 243 scenarios, respectively. Figures 3c and d show the progress of the solution for the third and fifth sets of instances in Table 2, having 81 and 243 scenarios, respectively. All four figures highlight that ScenPredOpt reduces the objective function value at a faster rate compared to Gurobi. In addition, the progress of the objective value stabilizes earlier, underlining the success of ScenPredOpt.

Fig. 3
figure 3

Progress of Gurobi and ScenPredOpt objective values during the first few seconds of the solution process. All solution times are given in CPU seconds

Full size image

6.1.2 Instance-by-Instance results and comparison with PredOpt

In Table 3, we present the instance-by-instance results for 10 SMCLSP instances with larger scenarios than the previously-presented ones. The problem contains 8 items, 13 periods, and 2 scenarios per stage without scenario-cap**. Therefore, each instance contains 4096 scenarios. The results are generated using the 8-item model in Table 1. The Gurobi does not reach an optimal solution for any problem within the given 2-hour solution time limit. In addition, SDDiP cannot reach a better solution than Gurobi in a given 20-stable iteration limit. The solution time of ScenPredOpt changes between 80 and 882 s. The heuristic has a higher solution time than ScenPredOpt for all 10 instances within the range of 1222 to 2086 s. This translates to a higher time-improvement factor of ScenPredOpt compared to the heuristic for all instances. Also, the optimality gaps between ScenPredOpt and heuristic differ considerably in favor of the ScenPredOpt. Table 3 demonstrates that ScenPredOpt is not only dominant in averages but also superior in instance-by-instance cases compared to the heuristic solution times and the optimality gap and solution time of exact approaches. Furthermore, Table 3 presents a comparison between ScenPredOpt and the PredOpt introduced in Yilmaz and Büyüktahtakın (2024). The solution time of PredOpt is denoted by timePredOpt, the time improvement factor achieved by PredOpt is denoted by timeImpPredOpt, and the resulting optimality gap is denoted by optGapPredOpt. In 8 over 10 instances, ScenPredOpt outperforms PredOpt in terms of both the solution time and the optimality gap. In instance 2, ScenPredOpt has a better optimality gap than PredOpt, but with a slightly higher solution time. The third instance presents the opposite case, where ScenPredOpt has a better solution time with a larger optimality gap compared to PredOpt. The averages highlight the superiority of ScenPredOpt over PredOpt, with the former having a lower average solution time, a higher time improvement, and a lower optimality gap.

Table 3 Detailed results of experiments for SMCLSP with 8 items
Full size table

To summarize the results presented in Tables 1, 2, and 3 and Fig. 3, ScenPredOpt achieves a better solution than the heuristic and PredOpt in a statistically faster process. The optimality gap of state-of-the-art SDDiP is lower than that of ScenPredOpt at the cost of significantly increased solution time. Therefore, ScenPredOpt can be a favorable alternative to Gurobi and SDDiP by providing a fast and high-quality solution at a fraction of the computational cost without requiring expert knowledge about the problem solved.

6.2 Quality of predictions for SMSMK

Table 4 presents the first set of results for SMSMK. The model is trained with \(T=30\)-period instances. For the first set with 32 scenarios, the solution time is reduced from more than 1000 s with Gurobi to only one second with ScenPredOpt. This is much faster compared to the heuristic with a better optimality gap, i.e., a 2.73% gap with the heuristic compared to 1.09% with ScenPredOpt. The PH improves the Gurobi solution time for most cases with a slight optimality gap, but it is much slower compared to the heuristic or ScenPredOpt. For example, PH reduces the solution time more than half with only a 0.02% optimality gap in almost 2000 s in the fourth test set of Table 4. The ScenPredOpt can provide a solution in less than 5 s with only a 0.82% optimality gap. While the heuristic outperforms PH in solution time, ScenPredOpt outperforms the heuristic in terms of both solution time and optimality gap. Also, all p-values of the Wilcoxon signed-rank are smaller than 0.01 highlighting the success of the ScenPredOpt over the heuristic.

Table 4 Average results of experiments for SMSMK with 8 items
Full size table

Table 5 presents another set of instances for SMSMK with 10 items. The results highlight the quality of the ScenPredOpt solution over the heuristic and the time improvement over Gurobi and PH, similar to Table 4. For example, in the last data set with 512 scenarios, the solution time is reduced to almost a minute from two hours. This significant time improvement factor of 150 is achieved with an optimality gap of only 0.77%. Similarly to the tables presented previously with SMCLSP and SMSMK, all p-values for the Wilcoxon test are less than 0.01. Also, the optimality gaps of the heuristic are much larger than those of the ScenPredOpt for all instances. Furthermore, LP-relaxation enhances ScenPredOpt accuracy.

Table 5 Average results of experiments for SMSMK with 10 items
Full size table

To sum up Tables 4 and 5, ScenPredOpt achieves a significant reduction in solution time compared to Gurobi and PH at the cost of a small optimality gap. Also, it outperforms the heuristic in terms of solution quality and time for all cases. Thus, ScenPredOpt is a promising alternative to other exact and heuristic algorithms for generating fast but high-quality solutions to complex problems that need to be solved repeatedly and quickly. Furthermore, both models are tested with the parameters given for the two-stage problem and the results are presented in Appendix B.

6.3 Generalization: quality of predictions for item-wise expansion algorithm

In this section, we present the computational results for test sets with a larger number of items than the models are trained with. In the previous section, the results showed that the models can maintain high-quality solutions with the increasing number of periods and scenarios. The expansion in the period dimension is organic since encoder-decoder models can handle variable-length input and output structures. Also, the presented NEDA model can handle a varying number of scenarios by averaging different groups of scenarios based on the scenario tree of the problem using Eq. (5). This provides substantial flexibility to solve instances with a changing number of scenarios and periods. However, predicting a problem with a different number of items is not straightforward with the NEDA, since the predictions are made using a fixed-length output. Algorithm 2 presents an item-wise expansion algorithm that can generate predictions for a problem with a large number of items using a model trained with a small number of items. The main idea is to generate predictions for a subset of items multiple times with the trained model of a fixed number of items and combine them to generate a final prediction for all items considered in the test instance. This algorithm provides significant benefits, as a trained model has the potential to make predictions for a problem with any number of periods, scenarios, and items for a certain distribution of input data. Therefore, the ScenPredOpt framework can provide high levels of flexibility without generating training instances and performing training for the new set of instances with a larger number of items. Furthermore, we compare this with the item-wise expansion strategy presented in Yilmaz and Büyüktahtakın (2024) and show that the deviation-based item-wise expansion method is a further improvement over the former one. For these results, we use metrics timePredOpt, timeImpPredOpt, optGapPredOpt, and optGapPredOpt.

Table 6 presents the results of the item-wise expansion for the SMCLSP. The first three sets of results are generated using the model trained with 8 items in Table 1, and the last three sets of results are generated using the model trained with 12 items in Table 2. The results demonstrate that the ScenPredOpt used within the item-wise expansion algorithm can provide high-quality solutions. For example, in the third set of instances with 16 items, predictions from the 8-item model yield a time improvement of 300, which is significantly more than the heuristic time improvement of 65. In addition, the optimality gap of ScenPredOpt is 0. 09%, which is 20 times lower than the heuristic optimality gap of 1.84%. Also, in the first, second, fourth, and fifth datasets, ScenPredOpt outperforms SDDiP in terms of optimality gap and solution time. For all the test sets in Table 6, ScenPredOpt outperforms the heuristic in terms of solution time and optimality gap. Also, all p-values for the Wilcoxon signed-rank test are all lower than 0.01, confirming that ScenPredOpt is statistically faster than the relax-and-fix heuristic. Moreover, ScenPredOpt outperforms PredOpt in terms of optimality gap in 3 out of 6 test sets and has the same average optimality gap for the remaining 3 instances at the cost of reduced time improvement. Therefore, the variance-based item-wise algorithm achieves a better optimality gap compared to Yilmaz and Büyüktahtakın (2024).

Table 6 Average results of generalization experiments for SMCLSP
Full size table

Table 7 presents the item-wise expansion results for SMSMK, similar to Table 6. The first three results are produced with the 8-item model in Table 4, and the remaining three sets of results are produced using the 10-item model in Table 5. The results highlight that the models can be used to predict instances with a varying number of items coming from the same distribution using Algorithm 2. The instances presented in Table 7 do not terminate within a set solution time limit of 7200 s and achieve significant optimality gaps with Gurobi. For example, Gurobi achieves an optimality gap of 0.67% for the second dataset. The ScenPredOpt terminates in only 13 s on average and achieves a 0.70% optimality gap compared to the best solution found by Gurobi. For the same test set, the heuristic terminates in 27 s with a larger gap of 1.07%. On average, ScenPredOpt reduces the solution time by more than 700, with an optimality gap below 1%. The heuristic has an average time improvement factor of 377 with a larger gap. We also conclude that the ScenPredOpt is faster than the heuristic since p-values for the Wilcoxon signed rank test are below 0.01 except for the fourth test set. Additionally, the variance-based item-wise strategy given in Algorithm 2 outperforms the strategy given by Yilmaz and Büyüktahtakın (2024) in terms of the optimality gap for all test sets in Table 7. On average, the reduction of the optimality gap with Algorithm 2 is greater than 0. 2% with an increased average solution time of 6 s. In addition, the accuracy of the fixed binary variables is increased by more than 2% as a result of the LP-relaxation in the ScenPredOpt framework.

Table 7 Average results of generalization experiments for SMSMK
Full size table

In summary, the ScenPredOpt framework with the variance-based item-wise expansion algorithm can be used to predict instances with a varying number of items. This provides significant flexibility for model training, since training can be performed using problems with a small number of items, which is easier to solve. Also, trained models do not need to retrain with changing number of items. Tables 6 and 7 provide the generalization results, in which ScenPredOpt outperforms the heuristics in terms of solution time and quality in 11 of 12 instances. Furthermore, Algorithm 2 reaches a better or the same optimality gap as Yilmaz and Büyüktahtakın (2024) at the cost of an increased solution time.

Table 8 Details of test instances for SMCLSP
Full size table

7 Conclusions and future work

In this study, we presented a learning-enabled framework for solving scenario-based multi-stage stochastic programs. We address the non-anticipativity of predicted variables by develo** the NEDA based on attentional encoder-decoder models. Additionally, generating labels for training instances can be untraceable when considering significant training data requirements. We overcome this issue by sampling a scenario and solving this deterministic problem to optimality, which is used for training. Furthermore, we present the ScenPredOpt algorithm to utilize the predictions without causing any infeasibility. We integrate an LP-based heuristic to further reduce the solution time and to integrate heuristic solution capabilities that might not be captured with a learning methodology. We present the results of our framework by generating benchmark instances with a commercial solver, exact approaches, and heuristics. The results show that the solution time can be reduced by three orders of magnitude by achieving a small optimality gap of less than 1%. Additionally, we present a variance-based item-wise expansion algorithm and test if the models can be used to predict instances with a larger number of items than they are trained with. The results show that the trained models and ScenPredOpt provide a high amount of flexibility and can be utilized to solve instances with varying stages, scenarios, and items. Our framework is general and can be utilized to solve scenario-based multi-stage stochastic programs with binary variables where such problems need to be solved repeatedly quickly, such as resource allocation, price optimization, and scheduling.

We have demonstrated the applicability of our methodology in the context of two prominent multi-stage stochastic programs: multi-item lot-sizing and dynamic knapsack. The multi-item lot-sizing problem can be relaxed to the multi-item knapsack problem (Pochet & Wolsey, 2006). The multi-item knapsack problem resembles the broader class of general multi-stage stochastic MIPs. By considering diverse dimensions, such as items, locations, products, processes, and more, our approach accommodates a flexible framework. Consequently, our item-wise expansion method can be employed to enhance the scalability of predictions to larger instances, applying to a variety of dimension types.

Our study shows a way to successfully integrate learning models, heuristics, and existing mathematical solvers to achieve significant reductions in solution time. In this way, the best of each approach can be used. The scenario-based multi-stage stochastic programs have a wide range of applications in which learning-based frameworks can be exploited. Further studies can focus on solving multi-stage stochastic programs by integrating scenario-generation mechanisms into the framework. Further studies can focus on advancing the scalability of the proposed ScenPredOpt framework for larger dimensional instances. Also, risk-averse stochastic programs can be tackled by adjusting the NEDA model, the probability of scenarios and the distribution of uncertain elements. Another direction relates to the integration of heuristics. Instead of general LP-based heuristics, problem-specific heuristics can be integrated into the ScenPredOpt solution framework to achieve better solutions faster.