Multi-item order quantity optimization through stochastic goal programing

Abstract

Managing multi-item economic order quantity (MIEOQ) problems within an uncertain business environment is a critical challenge. Decision-makers, with a comprehensive understanding of organizational goals and risk tolerances, play a pivotal role in this context. However, existing solutions often inadequately consider decision-maker preferences in MIEOQ problem-solving. The literature suggests that integrating the concept of satisfaction function with stochastic goal programming (SGP) can address this issue. However, the existing SGP approaches struggle with the challenge of effective goal setting. Additionally, employing distinct satisfaction functions for each uncertain goal can complicate threshold setting, diminishing their effectiveness. To tackle these challenges, we introduce a straightforward, yet effective approach called aspiration-free goal programming (AFGP) and integrate it with a unified satisfaction function. AFGP operates by minimizing expected values of deviation variables, eliminating the challenging task of goal setting under uncertainty. A unified satisfaction function is a singular metric applied uniformly across multiple goals, offering a consistent framework for evaluating performance across diverse objectives. This integration forms a preference-sensitive framework that not only captures nuanced trade-offs between conflicting objectives but also enhances decision quality and stakeholder satisfaction. By emphasizing the importance of decision-maker’s preferences and addressing identified issues, our research introduces a practical and effective approach for achieving balanced solutions in uncertain MIEOQ environments.

1 Introduction

In today's rapidly changing and highly competitive business environment, managing multi-item economic order quantity (MIEOQ) problems under uncertain conditions is a significant challenge. These problems are fundamental to effective inventory management and directly impact a company's operational efficiency and financial performance. The complexity of these issues stems from the need to determine the best order quantities for multiple items while dealing with various sources of uncertainty. These uncertainties can result from unpredictable shifts in demand, unforeseen disruptions in the supply chain, or rapidly changing market conditions. The challenge becomes even more overwhelming when dealing with many items, each with its own unique demand patterns and supply limitations.

In this context, effective decision-making extends beyond mere operational efficiency; it evolves into a strategic imperative. Inadequate inventory management can give rise to a dual dilemma. On one hand, excessive stock levels can result in elevated holding costs and the risk of wastage. Conversely, insufficient stock levels pose their own array of challenges, such as the specter of stockouts, lost sales, and disgruntled customers. In a marketplace where customer satisfaction is the ultimate competitive advantage, the ability to promptly fulfill customer demands emerges as a matter of paramount significance. Any deficiency in addressing this critical aspect can lead to the attrition of valuable clientele and detriment to the company's brand reputation.

Several multi objective programming (MOP) approaches have been employed to tackle MIEOQ problems under uncertainty, including stochastic goal programming (SGP), fuzzy goal programming, and heuristics. However, the solutions fall short in explicitly considering the decision-maker's preferences. Incorporating decision-maker’s preferences into the problem-solving process under conditions of uncertainty is pivotal for several reasons. It ensures that the solutions are strategically aligned with the organization's goals, as decision-makers possess a comprehensive understanding of the overarching objectives. Furthermore, it facilitates the mitigation of risks by allowing for the consideration of the decision-maker's specific risk tolerances. The adaptability and customization provided by this approach enable a fine balance between conflicting objectives and offer resilience to changing uncertainties. Ultimately, decision-maker’s preferences are a crucial component in enhancing the problem-solving process, allowing it to effectively navigate the challenges presented by uncertain environments while maintaining a focus on the organization's strategic objectives and risk management.

This study aims to address the research question: How can MIEOQ problems, operating in an uncertain environment, be efficiently resolved while deliberately incorporating the decision-maker's preferences into the decision-making process? The multi-objective programming (MOP) literature suggests that integrating the concept of satisfaction function with SGP can provide an effective framework for tackling this challenge. SGP is an extension of traditional goal programming (GP), which incorporates stochastic or probabilistic elements to account for uncertainty and variability in the goal achievement process. A satisfaction function quantifies how well a specific goal is achieved within a given decision-making scenario and measures the degree to which a solution aligns with the desired goals.

SGP offers distinct advantages over other methodologies when confronting similar challenges. A key feature of SGP lies in its adept consideration of probabilistic aspects, presenting a more realistic portrayal of uncertainty. By incorporating uncertainty, SGP ensures a comprehensive understanding of the variability inherent in real-world scenarios, allowing decision-makers to assess potential scenarios with a deeper awareness of associated probabilities, thus enhancing decision quality. Moreover, SGP offers flexibility and adaptability, enabling model adjustments in response to changing uncertainties, making it well-suited for dynamic environments.

However, a challenge with employing SGP is that the decision-maker needs to set a goal (an aspiration level) for every objective, which can be particularly problematic in situations marked by high levels of uncertainty. Uncertainty in various aspects of decision-making, such as resource availability, demand fluctuations, supply chain disruptions, and market dynamics, can make it difficult to precisely determine the desired goals. This problem becomes even more noticeable when dealing with complex situations where multiple conflicting objectives need to be considered, like the case with MIEOQ problems.

Furthermore, in cases where goals exhibit conflicts and uncertainty, the decision-maker may find it necessary to continually adapt their preferences by adjusting the form and/or thresholds of the satisfaction functions until a balanced solution is attained. However, using distinct satisfaction functions for each goal can complicate this adjustment process and may lead to a complex web of individual functions, each with its specific parameters and thresholds, potentially leading to a less intuitive and more convoluted decision-making process.

To overcome these limitations, we propose a straightforward, yet effective approach called aspiration-free goal programming (AFGP), which is seamlessly integrated with a unified satisfaction function to address multi-item economic order quantity (MIEOQ) problems. AFGP operates on the fundamental principle of minimizing the sum of expected deviations, as opposed to their actual values. This distinctive feature eliminates the necessity for defining specific goals or aspiration levels, providing a more flexible and adaptive solution framework.

By excluding explicit goal setting from the solution process and using normalized expected deviations, AFGP allows for the application of a unified satisfaction function across all goals. This approach not only empowers the decision-maker to explicitly integrate their preferences regarding expected deviations but also streamlines the adjustment of preferences to attain a more satisfactory solution.

This study makes a substantial contribution by identifying a critical gap in existing approaches to solving MIEOQ problems. Specifically, it underscores the significant shortcoming of not incorporating decision-maker’s preferences into the problem-solving process. This recognition serves as the foundational impetus for introducing a novel approach, AFGP, and integrating it with a unified satisfaction function to address this limitation. By introducing this approach, our paper offers a practical and effective solution to the identified problem, significantly enhancing the decision-making process and promoting more balanced and adaptable solutions in uncertain environments.

The remainder of this paper is structured as follows: Sect. 2 provides a comprehensive review of the existing literature on MIEOQ problems and models, GP and SGP modeling, satisfaction functions, and SGP formulations. In Sect. 3 the AFGP approach is introduced. Section 4 presents the AFGP formulation of MIEOQ. Section 5, provides an illustrative example, offering a deeper understanding of the proposed model. We conclude with some final remarks in Sect. 6.

2 Literature review

2.1 MIEOQ problem categories

Practical multi-item economic order quantity (MIEOQ) problems inherently encompass multiple, often conflicting, objectives. Within the realm of inventory management, these objectives primarily revolve around minimizing costs, maximizing profits, ensuring timely deliveries to satisfy customers, and optimizing the utilization of available storage space.

The MIEOQ problems discussed in the literature can be grouped into six distinct categories including independent replenishment problems, joint replenishment problems, dynamic lot-sizing problems, capacitated lot-sizing problems, demand stochastic order quantity problems, periodic order quantity problems, and finally, multi-factor stochastic order quantity problems, which is the focus of our study.

Independent replenishment problems involve determining optimal order quantities for several items, often considering quantity discounts, limited storage capacity, and discrete delivery orders. For instance, Khalilpourazari et al. (2019c) introduce a multi-item EOQ model with imperfect items and stochastic operational constraints, optimizing order and backorder sizes for each item to maximize the total profit. Additionally, Khalilpourazari and Pasandideh (2020) propose a multi-objective optimization approach, utilizing meta-heuristic algorithms to solve the multi-item EOQ model with partial backordering, defective batches, and stochastic constraints.

The joint replenishment problems deal with the simultaneous replenishment of multiple items to optimize ordering costs. Ai et al. (2021) introduce an approach for optimizing joint replenishment for non-instantaneous deteriorating items with quantity discounts, utilizing the Improved Moth Flame Optimization (IMFO) algorithm to solve the model. Additionally, Liu et al. (2023) address this problem by develo** an efficient algorithm based on dynamic programming and branch-and-bound techniques.

Dynamic demand patterns necessitate tackling the dynamic lot-sizing problems, involving determining order quantities that adapt over time. Buschkühl et al. (2010) present a review of four decades of research on dynamic lot-sizing with capacity constraints, discussing various modeling and algorithmic solution approaches. Kulkarni and Bansal (2022) study single-item discrete multi-module capacitated lot-sizing problems where the amount produced in each time period is equal to the summation of binary multiples of the capacities of different modules or machines.

The capacitated lot-sizing problems encompass the challenge of determining optimal order quantities for multiple items while adhering to capacity constraints. Jalal et al. (2023) delve into the robust multi-plant capacitated lot-sizing problem with uncertain demands, processing, and setup times, addressing the complexities of a production system with multiple production plants.

The periodic order quantity problems require determining order quantities at regular intervals for multiple items, considering factors like deterioration and varying demands. Budiman et al. explore the economic order quantity model for deteriorating multi-items when constraints of storage capacity are active. The demand stochastic order quantity problems navigate the complexities of stochastic demand patterns for multiple items. Mubiru (2013) adopts a Markov decision process approach to determine the economic order quantity (EOQ) that minimizes inventory costs of multiple items under a periodic review inventory system with stochastic demand. Meisheri et al. (2022) propose a novel reinforcement learning approach for multi-product inventory control, considering dynamic and stochastic demand for multiple products and aiming to maximize long-term profit while satisfying customer service levels.

Lastly, multi-factor stochastic order quantity problems introduce complexities beyond uncertain demand, encompassing stochastic factors such as costs, time, quality, and resources. The next section provides an overview of these problems and the methodologies employed for their resolution.

2.2 MIEOQ modeling

Various methodologies are proposed to model and solve MIEOQ problems under uncertainty. Our literature study shows that stochastic goal programming (SGP), fuzzy goal programming and Heuristics are the most popular methods used in this context. In the following we review the most recent papers which have modeled a variation of the multi-item EOQ problem under uncertainty.

Stochastic goal programming¹

In their study, Nalubowa et al. (2022) investigate multi-objective optimization in the context of manufacturing lot size decisions under stochastic demand, emphasizing the challenge of simultaneously optimizing conflicting objectives. Their approach involves Markov chains and stochastic goal programming, ensuring comprehensive decision-making by considering goal constraints, deviation variables, priorities, and objective functions. Meanwhile, Liu et al. (2014) delve into order quantity allocation problems from the perspective of manufacturers contending with supply uncertainty. Their work presents a multi-objective mixed-integer stochastic programming model, addressing supply timing and quantity uncertainties while offering a two-phase heuristic approach. Nasiri and Davoudpour (2012) propose an integrated multi-objective distribution model. Their research explores optimizing conflicting objectives, including distribution costs, customer service levels, resource utilization, and delivery time, in the presence of uncertain forecast demands. Panda et al. (2008) tackle single-period inventory models with imperfections, stochastic demand, and various constraint types. They introduce mathematical models capable of handling stochastic and imprecise constraints, offering practical insights into profit functions' sensitivity. Lastly, Salas-Molina et al. (2020) address cash management systems and the management of multiple conflicting goals in the face of uncertainty. Their work introduces a stochastic goal programming model for cash management, considering various objectives and the inherent uncertainty in expected cash flows.

Fuzzy goal programming

Bera et al. (2009) study a multi-item mixture inventory model with budget constraint where both demand and lead-time are random. They use fuzzy chance-constrained programming technique and surprise function to transform the optimization problem into a multi-objective optimization problem. They develop an algorithm procedure to find the optimal order quantity and optimal value of the safety factor. Björk (2012) develops a fuzzy multi-item economic production quantity model where cycle times are uncertain. He handles uncertainty with triangular fuzzy numbers and finds an analytical solution to the optimization problem. Byrne (1990) presents an approach to the multi-item production lot-sizing problem based on the use of simulation to model the interactions occurring in a system where items share manufacturing facilities, and demands and lead times are stochastic. To achieve a minimum total cost solution, a search algorithm is applied to adjust the lot sizes based on the results of previous simulation runs. Dash and Sahoo (2015) present the optimization of a multi-item news-boy problem, where the demand is considered as a fuzzy random variable and the purchasing cost as a fuzzy number. They obtain the optimum order quantity by using Buckley's concept, which transforms a fuzzy single period inventory model into a crisp model. Panda et al. (2008) consider a multi-item economic order quantity model in which the cost parameters are of fuzzy or hybrid nature. They use the “surprise function” for the constraints to transform the problems into equivalent unconstrained deterministic and equivalent multi-objective inventory problems, respectively. Mondal and Maiti (2003) propose a soft computing approach to solve non-linear programming problems under fuzzy objective goal and resources with/without fuzzy parameters in the objective function. They use genetic algorithms (GAs) with mutation and whole arithmetic crossover. They formulate fuzzy inventory models as fuzzy non-linear decision-making problems and solved by both GAs and fuzzy non-linear programming (FNLP) method based on Zimmermann’s approach. Khalilpourazari et al. (2019a, 2019b, 2019c) propose new mathematical models for multi-item economic order quantity model considering defective supply batches and apply basic chance constraint programming, robust fuzzy chance constraint programming, and meta-heuristic algorithms to deal with uncertain parameters and operational constraints.

Heuristics

Levén and Segerstedt (2007) introduce a heuristic scheduling policy for a multi-item, single-machine production facility that checks that the presumed optimal order quantities obtain a feasible production schedule need to be modified to achieve a feasible solution. They discuss how the policy can also consider stochastic behaviour of the demand rates and compensate the schedule by applying appropriate safety times. Song et al. (2000) consider a single-period multi-item economic order/production quantity and time problem, where the procurement lead-time and demand are random. They present some structural results and present several simple heuristic policies and compare them to optimal policies.

Other methods

Fergany (2016) proposes a new general probabilistic multi-item, single-source inventory model with varying mixture shortage cost under two restrictions on the expected varying backorder cost and the expected varying lost sales. He formulates a model to analyze how the firm can deduce the optimal order quantity and the optimal reorder point for each item when demand is random but lead-time is constant. Gao et al. (2020) develop a multi-period, multi-item periodic-review dynamic programming model to address the raw-material inventory management problem in a foundry enterprise assuming carbon cost is only incurred during the transportation. They use the model to compare two production strategies: (i) scale down the original consumption rate of raw materials in an equal proportion on the premise of maximizing meeting the carbon emission limit, and (ii) keep the original raw material consumption rate constant in early stage and stop production when the carbon emissions are saturated. They propose a mathematic algorithm based on probabilistic dynamic programming (PDP) to derive the structural properties of the model. Jaya et al. (2012) develop multi-items inventory models by considering product expire date and quantity unit discount for stochastic demand environment. They use simulation and genetic algorithm to solve the models. Finally, Zhou (2010) studies a multi-item model in which a retailer faces a minimum order size requirement from its manufacturer and the demands for these items are stochastic. He constructs the exact model and develop an accurate lower bound approximation.

2.3 Goal programming and stochastic programming in MOP framework

Multi-objective programming (MOP) deals with optimization problems that entail the simultaneous optimization of multiple objective functions. MOP is employed when making optimal decisions involves managing trade-offs among two or more conflicting objectives. Consequently, for MOP problems, finding a single solution that optimizes all objectives simultaneously is often challenging, if not impossible. Without additional subjective preference information, an MOP problem may yield a (potentially infinite) number of Pareto optimal solutions, all deemed equally valid. A solution is termed Pareto efficient when improving one objective function's value necessitates a degradation in another objective's value. MOP problems are approached from various perspectives, resulting in different solution philosophies and objectives during their formulation and resolution. When emphasizing the decision-making aspect, the primary goal of solving an MOP problem is to assist the decision-maker in identifying the Pareto optimal solution that aligns most closely with their subjective preferences (Branke et al., 2008).

Depending on how the decision-maker's preferences are considered, MOP methods can be classified into four categories (Ching-Lai & Abu Syed, 1979): “no-preference”, “a priori”, “a posteriori”, and “interactive” methods. While in the first category the decision-maker is not involved, the other three categories incorporate the decision-maker's preferences in distinct ways. In priori methods, the decision-maker provides their preference information, and a solution that best satisfies these preferences is then determined. Sufficient preference information must be expressed prior to initiating the solution process (Hwang & Masud, 1979). In posteriori methods, a set of representative Pareto optimal solutions are initially identified, and the decision-maker subsequently selects one of them. In interactive methods, the decision-maker iteratively searches for the most preferred solution. In each iteration of the interactive method, the decision-maker is presented with Pareto-optimal solutions, and they describe how these solutions could be improved. The information provided by the decision-maker is then taken into account when generating new Pareto-optimal solutions for the decision-maker to examine in the next iteration. This process allows the decision-maker to gain insights into the feasibility of their preferences and focus on solutions that align with their interests. The decision-maker can choose to conclude the search at their discretion.

A well-known example of priori methods is goal programming (GP) first used by Charnes et al. (1955). In GP, each objective is given a goal or target value to be achieved. Unwanted deviations from these set target values are then minimized in an achievement function. This approach is based on a satisfying philosophy, which means the aim is not necessarily to find the optimal solution, but rather a solution that is “good enough” or satisfies the minimum requirements.

The satisfying philosophy of GP contrasts with the efficiency philosophy commonly found in optimization. While the efficiency philosophy seeks the optimal solution that maximizes or minimizes the objective function, the satisfying philosophy of GP seeks a solution that meets the goals or targets set for each objective (Jones & Florentino, 2022). This makes GP particularly useful in situations where the decision-maker has specific goals or targets for each objective. GP has been widely used in various fields however, it’s important to note that GP models have the downside of potentially generating solutions that are not Pareto efficient. Despite this, there are ways to improve Pareto efficiency within the GP framework (Gütmen et al., 2023).

While deterministic optimization problems are typically formulated with known parameters, real-world problems often involve varying degrees of uncertainty. Stochastic Programming, initially formulated by Dantzig in 1955, is designed to model this uncertainty and seeks to find solutions that remain feasible for all (or nearly all) potential instances of uncertain parameters. Stochastic Programming is an optimization approach in which some or all problem parameters are characterized by uncertainty but follow known probability distributions (Birge & Louveaux, 2011). This framework stands in contrast to deterministic optimization, where all parameters are assumed to be precisely known. The fundamental goal of stochastic programming is to identify a decision that not only optimizes specific criteria chosen by the decision-maker but also effectively accommodates the uncertainty associated with problem parameters.

Stochastic goal programming (SGP) seamlessly integrates the principles of stochastic programming and goal programming, creating a comprehensive framework that effectively addresses multi-objective problems in uncertain decision-making environments. In this approach, each objective function is assigned a goal that is subject to stochastic or uncertain events (Masri, 2017). This allows the decision-maker to manage risk and uncertainty while still striving to achieve their goals. SGP provides a robust and flexible framework for multi-objective optimization in the presence of uncertainty, allowing decision-makers to balance multiple conflicting objectives while taking into account the inherent uncertainties in real-world decision-making scenarios (Al Qahtani et al., 2019).

2.4 Satisfaction function

The satisfaction function, originally introduced by Martel and Aouni in 1990, is a crucial concept in the domain of multi-objective optimization and decision-making. It provides decision-makers with a structured framework to articulate their preferences regarding the disparities between actual achievement and desired aspiration levels for each objective. This function enables decision-makers to quantify the extent of concessions or improvements they are willing to make for each objective, allowing for a balanced approach in handling trade-offs. Through scenario analyses, decision-makers can evaluate how changes in their preferences influence the resulting solutions, enhancing their understanding of solution sensitivity and trade-off dynamics in multi-objective optimization problems.

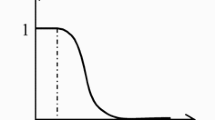
The general form of the satisfaction function is demonstrated in Fig. 1, where ${\text{S}}_{{\text{i}}} \left( {{\updelta }_{{\text{i}}} } \right)$ represents the satisfaction level associated with deviation ${\updelta }_{{\text{i}}}$, and ${\upalpha }_{id}$, ${\upalpha }_{i0}$, and ${\upalpha }_{iv}$ denote the “indifference”, the “nil”, and the “veto” thresholds, respectively. According to the model, when the deviations ${\updelta }_{{\text{i}}}$ falls within the interval $\left[ {0,{\upalpha }_{id} } \right]$ the decision-maker is perfectly satisfied, and the satisfaction level reaches “1” which is the maximum value. The satisfaction decreases when the deviation falls within the interval $\left[ {{\upalpha }_{id} ,{\upalpha }_{i0} } \right]$. Within the interval $\left[ {{\upalpha}_{i0} ,{\upalpha}_{iv} } \right]$, the decision-maker will be dissatisfied but the solutions are accepted. The solutions leading to deviations that exceed ${\upalpha }_{iv}$ are rejected.

Fig. 1

General shape of the satisfaction functions

The degree of satisfaction is contingent on the differences between the aspirated levels and the achieved level. Smaller differences result in a higher level of satisfaction for the decision-maker. Moreover, the satisfaction function concept is versatile, allowing for the modeling of imprecision related to goal values through decision-maker-defined intervals, showcasing its adaptability to various contexts.

Applications of the satisfaction function within the stochastic goal programming (SGP) are diverse and impactful. For instance, it has been utilized in stock exchange market portfolio selections, supply chain strategic and tactical decision-making, and optimal labor allocation. The satisfaction function's role in SGP is akin to that of the membership function in fuzzy goal programming (FGP) or the penalty function in goal programming with interactive fuzzy goals (GPI). However, the satisfaction function excels by explicitly incorporating decision-makers' preferences and not necessitating symmetry or linearity, offering a robust approach to preference modeling within SGP (Cherif et al., 2008). This integration of preference modeling makes the satisfaction function a powerful tool in addressing imprecision and enhancing decision-making processes.

2.5 SGP formulations

A widely employed mathematical programming model for tackling MOP problems is deterministic goal programming (GP) introduced by Charnes and Cooper (1955). One of the primary strengths of GP is its direct engagement of decision-makers in the formulation process. This involvement allows decision-makers to actively participate in setting goals and determining the relative importance of each goal. Consequently, GP ensures a solution that is more pertinent and meaningful, incorporating critical insights vital for the model's accuracy.

Serving as an extension of linear programming, GP focuses on achieving predefined target values for a set of goals rather than seeking an optimal solution confined by strict constraints. In a typical form of GP, as demonstrated in Program 1, the objective is to minimize the weighted sum of variables $\updelta_{i}^{ + }$ and $\updelta_{i}^{ - }$ which respectively represent the positive and negative deviations between the achievement levels and the goals (or aspiration levels) denoted by $g_{i}$.

$$ \begin{aligned} & Min \mathop \sum \limits_{i = 1}^{m} \left( {w_{i}^{ + } \delta_{i}^{ + } + w_{i}^{ - } \delta_{i}^{ - } } \right) \\ & s.t. \mathop \sum \limits_{j = 1}^{n} \left( {a_{ij} x_{j} - \delta_{i}^{ + } + \delta_{i}^{ - } } \right) = g_{i} \\ & \quad \delta_{i}^{ + } , \delta_{i}^{ - } \ge 0 \\& \quad i = 1; 2; . . . ; m \\ \end{aligned} $$

(1)

In Program 1, $m$ is the number of objectives, weights $w_{i}^{ + }$ and $w_{i}^{ - }$ represent the relative importance of $\delta_{i}^{ + }$ and $\delta_{i}^{ - }$, $x_{j}$ ​denotes the $j$ th decision variable, $a_{ij}$ ​indicates the coefficient of the $j$ th decision variable in the $i$ th constraint, and $n$ refers to the number of the decision variables.

Deterministic model parameters are not always available and/or appropriate. In such cases, stochastic goal programming (SGP) formulations have received attention. Introduced by Contini (1968), SGP deals with the uncertainty related to the decision-making situation. In such situations, decision-makers are unable to evaluate the certainty of parameters but can provide some information regarding the likelihood of occurrence of the parameter values (Aouni et al., 2012). Therefore, SGP aims to maximize the probability that the result of the decision fall within a certain region encompassing the uncertain goal.

Depending on the sources and types of uncertainty, the methods of handling uncertainty, and the structure of the objectives, different SGP models are employed to address a wide range of decision-making scenarios. These models offer distinct approaches to optimizing multiple objectives under varying degrees of uncertainty and priorities. Some of the models include scenario based SGP (Jayaraman et al., 2016), Fuzzy SGP (Van Hop, 2007), mean–variance SGP (Ballestero et al., 2001), recourse SGP (Masmoudi and Ben Abdelaziz, 2012), and multiple SGP (Masri, 2017). However, according to Ben Abdelaziz et al. (2007) the most popular model of SGP is chance-constrained goal programming (CCGP) which is based on chance-constrained programming (CCP) approach. This approach uses probability distributions to represent the uncertain parameters and imposes probabilistic constraints on the goals. Introduced by Charnes and Cooper (1959, 1963), CCP was initially designed to solve stochastic linear problems. The motivation behind CCP is to let decision-makers arrive at the most satisfactory solutions by striking a balance between the achievement levels of the objectives and the associated risks. In essence, CCP aims to maximize the expected value of the objectives while ensuring a specified probability of constraint realization (Azimian & Aouni, 2015).

Depending on the treatment of the constraints there are two distinct approaches for the CCP, namely the unconditional CCP and the joint CCP. The unconditional CCP considers the probability to realize each one of the constraints independently from the other and is formulated as follows:

$$ \begin{aligned} & Max E\left[ {f\left( {\underline {x} } \right)} \right] \\ & s.t. P\left[ {\mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} = \tilde{b}_{i} } \right] = \alpha_{i} \\ & \quad 0 < \alpha_{i} \le 1 \\ & \quad i = 1; 2; . . . ; m \\ \end{aligned} $$

(2)

The joint CCP assumes that the decision-maker is interested in the joint realization of the constraints and is modelled as:

$$ \begin{aligned} & Max E\left[ {f\left( {\underline {x} } \right)} \right] \\ & s.t. P\left[ {\mathop \sum \limits_{j = 1}^{n} a_{j} x_{j} = \tilde{b}} \right] = \alpha \\ & \quad 0 < \alpha \le 1 \\ \end{aligned} $$

(3)

CCP allows for addressing probabilistic uncertainty associated with various parameters of the problem, such as coefficients and goal values (Aouni et al., 2005). However, in its classical formulation of chance-constrained SGP, only goals are assumed to be stochastic following specific probability distributions (Jayaraman et al., 2016).

Keown (1978) and Keown and Taylor (1980) propose adapted models of CCP which transforms SGP into a nonlinear program. Keown and Martin (1977) and Keown (1978) are the first attempts to combine the SGP and CCP models. The lexicographic chance-constrained GP model of Keown and Martin (1977) can be formulated as:

$$ \begin{aligned} & lexmin \left[ {\mathop \sum \limits_{{i \in I_{1} }} \left( {\tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } } \right),\mathop \sum \limits_{{i \in I_{2} }} \left( {\tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } } \right), \ldots , \mathop \sum \limits_{{i \in I_{p} }} \left( {\tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } } \right)} \right] \hfill \\ & s.t.\quad \quad P\left[ {f_{i} \left( {\underline {x} } \right) \le \tilde{b}} \right] \ge \alpha_{i} \hfill \\ &\quad \quad \quad \underline {x} \in D \hfill \\ & \quad \quad \quad 0 < \alpha \le 1 \hfill \\ & \quad \quad \quad \tilde{\delta }_{i}^{ + } ,\tilde{\delta }_{i}^{ - } > 0 \hfill \\ & \quad \quad \quad i = 1,2, \ldots ,m \hfill \\ \end{aligned} $$

(4)

To explicitly incorporate the decision-maker’s preferences in the solution process, Aouni et al. (2005) propose a new formulation of SGP. Starting from a linear formulation of the SGP,

$$ \begin{aligned} & min \mathop \sum \limits_{i = 1}^{m} \left( {\tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } } \right) \\ & s.t. \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - \tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } = \tilde{g}_{i} \\ & \quad \quad \tilde{\delta }_{i}^{ + } ,\tilde{\delta }_{i}^{ - } > 0 \\ & \quad \quad i = 1,2, \ldots ,m \\ \end{aligned} $$

(5)

and assuming $\tilde{g}_{i} \in N\left( {\mu ,\sigma^{2} } \right)$, they formulate the deterministic equivalent of Program 5 as:

$$ \begin{aligned} & min \mathop \sum \limits_{i = 1}^{m} \left( {\delta_{i}^{ + } + \delta_{i}^{ - } } \right) \\ & s.t. \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - \delta_{i}^{ + } + \delta_{i}^{ - } = \mu_{i} \\ & \quad \quad \delta_{i}^{ + } , \delta_{i}^{ - } > 0 \\ & \quad \quad i = 1,2, \ldots ,m \\ \end{aligned} $$

(6)

Finally, incorporating the concept of the satisfaction function, Martel and Aouni (1990) model SGP as:

$$ \begin{aligned} & min \mathop \sum \limits_{i = 1}^{m} \left( {w_{i}^{ + } F_{i}^{ + } \left( {\delta_{i}^{ + } } \right) + w_{i}^{ - } F_{i}^{ - } \left( {\delta_{i}^{ - } } \right)} \right) \\ & s.t. \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - \delta_{i}^{ + } + \delta_{i}^{ - } = \mu_{i} \\ & \quad \quad i = 1,2, \ldots ,m \\ \end{aligned} $$

(7)

where $\mu_{i}$ represents the mean of goal $i$, variables $\delta_{i}^{ + }$ and $\delta_{i}^{ - }$ denote the positive and negative deviations from $\mu_{i}$, $F_{i}^{ + } \left( {\delta_{i}^{ + } } \right)$ and $F_{i}^{ - } \left( {\delta_{i}^{ - } } \right)$ are the satisfaction functions for the positive and negative deviations, and $w_{i}^{ + }$ and $w_{i}^{ - }$ refer to the corresponding weights.

Aouni and La Torre (2010) provide a different formulation of the SGP model. Given a probability space $\left( {\Omega ,\Im ,P} \right)$, where $\Omega$ is the space of events, $\Im$ is a sigma algebra on $\Omega$, and $P$ is a probability measure. They consider the aspiration levels $g_{i} :D \to R \left( {{\text{i}} = 1,2,...,{\text{p}}} \right)$, which are random variables with finite first-order and second-order moments, and introduce the following program for almost every $\omega \in \Omega$:

$$ \begin{aligned} & min \mathop \sum \limits_{i = 1}^{p} \left( {\delta_{i}^{ + } \left( \omega \right) + \delta_{i}^{ - } \left( \omega \right)} \right) \\ & s.t. f_{i} \left( {x,\omega } \right) - \delta_{i}^{ + } \left( \omega \right) + \delta_{i}^{ - } \left( \omega \right) = g_{i} \left( \omega \right) \\ & \quad \quad \delta_{i}^{ + } \left( \omega \right), \delta_{i}^{ - } \left( \omega \right) \ge 0 \\ \end{aligned} $$

(8)

Their work illustrates a method that requires more computational time than those based on equivalent deterministic problems. However, it offers a more detailed representation of the inherent complexity within the stochastic problem.

Abdelaziz et al. (2007) propose the following chance constrained compromise programming (CCCP) model based on the compromise programming (CP) and chance constrained programming (CCP) models where the parameters of the objectives are stochastic.

$$ \begin{aligned} & min \mathop \sum \limits_{i = 1}^{m} \delta_{i}^{ + } + \delta_{i}^{ - } + \varepsilon_{i}^{ + } + \varepsilon_{i}^{ - } + \mathop \sum \limits_{k = 1}^{p} \delta_{k}^{ + } + \delta_{k}^{ - } \\ & s.t.\, E\left( {\mathop \sum \limits_{j = 1}^{n} \tilde{a}_{kj} x_{j} - \tilde{g}_{k} } \right) + F^{ - 1} \left( {\alpha_{k} } \right).\sigma \left( {\mathop \sum \limits_{j = 1}^{n} \tilde{a}_{kj} x_{j} - \tilde{g}_{i} } \right) - \delta_{k}^{ + } + \delta_{k}^{ - } = 0 \\ & \quad \quad E\left( {f_{i}^{*} - \mathop \sum \limits_{j = 1}^{n} \tilde{C}_{ij} x_{j} } \right) + F^{ - 1} \left( {\alpha_{i} } \right).\sigma \left( {f_{i}^{*} - \mathop \sum \limits_{j = 1}^{n} \tilde{C}_{ij} x_{j} } \right) - \varepsilon_{i}^{ + } + \varepsilon_{i}^{ - } - \delta_{i}^{ + } + \delta_{i}^{ - } = 0 \\ \end{aligned} $$

(9)

In the above program, $\tilde{a}_{kj} x_{j}$ and $\tilde{g}_{k}$ represent the objective function and goal for objective $i$, $E\left( . \right)$ and $\sigma \left( . \right)$ are, respectively, the mean and the standard deviation functions, $F^{ - 1} \left( . \right)$ represents the inverse distribution function of the standard normal distribution, $\alpha_{i}$ refers to the desired level of probability for achieving $\tilde{g}_{i}$, and $\delta_{k}^{ + } {\text{and}} \delta_{k}^{ - }$ are the variables denoting the deviations between the goals and the achievement levels. Besides, $f_{i}^{*}$ denote the best solution of the objective function $\mathop \sum \nolimits_{j = 1}^{n} \tilde{C}_{ij} x_{j}$ where $\tilde{C}_{ij}$ as the maximum value observed for objective $i$, and $\alpha_{k}$ refers to the desired level of probability for achieving $f_{i}^{*}$.

Masmoudi and Ben Abdelaziz (2012) propose a recourse approach for solving the same problem. The model first minimizes the expected deviation between the objective function and the goal. The result is then used to inform and guide the decision-maker in making decisions in the recourse step.

Masri (2017) identifies two goals (acceptable and ideal goals) instead of a unique goal and extend the previous two works by introducing a new chanced-constrained approach called multiple stochastic goal programming and integrating that with the concept of penalty function (Martel & Aouni, 1990).

The aforementioned SGP formulations exhibit at least one of the following issues: neglecting the decision-maker's limitation in promptly specifying target values for stochastic goals, oversimplifying the problem by substituting the stochastic goals with their averages, and proposing a model that is overly intricate, particularly for complex problems like MOEOQ. In the next section, we introduce an intuitive approach that effectively addresses these issues by eliminating the need for decision-makers to set aspiration levels for stochastic goals.

3 Aspiration-free approach to SGP

Goal setting is a critical step in SGP which poses several challenges. Almost in all SGP extensions stochastic goals are either substituted by their means or represented by probabilistic thresholds set by the decision-maker. Using means to representing stochastic goals introduces several drawbacks. Firstly, this method oversimplifies the inherent stochasticity of the original goal distributions. Stochastic goals typically follow probability distributions, and relying on means neglects the variability and risk associated with these distributions. Consequently, solutions derived from this approach may fall short of capturing the entire spectrum of potential outcomes. Secondly, there is a significant loss of crucial stochastic information when stochastic goals are represented by means. While means provide a measure of central tendency, they fail to convey the complete distribution, which is essential for understanding the full range of potential outcomes. Thirdly, the use of means ignores decision-makers' risk preferences, a critical aspect when dealing with stochastic goals. Decision-makers may have specific attitudes towards risk, and stochastic goals inherently involve an element of uncertainty. Neglecting these risk preferences can lead to solutions that do not align with the decision-maker's tolerance for uncertainty. Lastly, the approach of using means might oversimplify the decision space, focusing solely on deviations from means. This oversimplification disregards the complexities involved in optimizing multiple objectives and making informed trade-offs. Particularly in dynamic and uncertain environments, this simplification can result in misleading outcomes, especially if decision results are sensitive to extreme values or outliers.

Representing stochastic goals by probabilistic thresholds allows for a more nuanced representation of uncertainty and provides a more realistic and flexible approach compared to using means. It allows decision-makers to explicitly consider the uncertainty associated with goal achievement and tailor the thresholds to their specific risk preferences. However, it comes with certain disadvantages. Firstly, accurately defining appropriate probabilistic thresholds can be a challenging task. The decision-maker needs a deep understanding of the problem context and the consequences associated with different probability levels. Setting thresholds too high might lead to overly optimistic expectations, while setting them too low might result in excessively conservative solutions. Secondly, the inherent probabilistic nature of goals introduces complexities in the decision-making process. The decision-maker must grapple with the uncertainty associated with achieving goals, making it difficult to precisely determine the desired probabilistic thresholds. This uncertainty can be exacerbated in situations with limited historical data or rapidly changing environments. Moreover, the process of setting probabilistic thresholds adds an additional layer of subjectivity to the decision-making process. Different decision-makers may have varying risk tolerances and preferences, leading to potential disagreements in the selection of appropriate thresholds.

To address these shortcomings, we introduce a straightforward, yet effective approach known as aspiration-free goal programming (AFGP). In AFGP, the objective is to minimize the expected value of deviations rather than their actual values. This approach eliminates the need for setting specific goals, thereby avoiding the disadvantages associated with using means or probabilistic thresholds.²

The SGP model can be reformulated as follows:

$$ \begin{aligned} & Min \mathop \sum \limits_{i = 1}^{I} \left( {w_{i}^{ + } \tilde{\delta }_{i}^{ + } + w_{i}^{ - } \tilde{\delta }_{i}^{ - } } \right) \\ & s.t. \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - \tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } = \tilde{g}_{i} \\ & \quad \quad \tilde{\delta }_{i}^{ + } ,\tilde{\delta }_{i}^{ - } \ge 0 \\ & \quad \quad i = 1,2, \ldots , I \\ \end{aligned} $$

(10)

where $\tilde{g}_{i}$ refers to the stochastic goal of the $i$ th objective, $a_{ij}$ ​ represents the coefficient for the $j$ th decision variable in the $i$ th objective, $x_{j}$ is the $j$ th decision variable, $\tilde{\delta }_{i}^{ + }$ and $\tilde{\delta }_{i}^{ - }$ refers to the positive and negative deviations, $w_{i}^{ + }$ and $w_{i}^{ - }$ denote the weights associated with positive and negative deviations for objective $i$, respectively, and $I$ is the number of the objectives.

Because solving the above problem as is proves difficult, if not impossible, and representing the goals by their means or probabilistic thresholds poses challenges, instead of attempting to minimize the sum of the actual values of deviations, $\tilde{\delta }_{i}^{ + } {\text{and}}\,\tilde{\delta }_{i}^{ - }$, we look into minimize the sum of the expected values deviations, ${\varvec{E}}\left( {\tilde{\delta }_{i}^{ + } } \right)$ and ${\varvec{E}}\left( {\tilde{\delta }_{i}^{ - } } \right)$, which are calculated as follows:

$$ {\varvec{E}}\left( {\tilde{\delta }_{i}^{ - } } \right) = \mathop \int \limits_{{\mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} }}^{\infty } \left( {\tilde{g}_{i} - \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} } \right)f\left( {\tilde{g}_{i} } \right)d\tilde{g}_{i} $$

(11)

$$ {\varvec{E}}\left( {\tilde{\delta }_{i}^{ + } } \right) = \mathop \int \limits_{ - \infty }^{{\mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} }} \left( {\mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - \tilde{g}_{i} } \right)f\left( {\tilde{g}_{i} } \right)d\tilde{g}_{i} $$

(12)

Assuming $\tilde{g}_{i}$ is normally distributed with mean of $\mu_{i}$ and standard deviation of $\sigma_{i}$, ${\varvec{E}}\left( {\tilde{\delta }_{i}^{ + } } \right)$ and ${\varvec{E}}\left( {\tilde{\delta }_{i}^{ - } } \right)$ can be written as:

$$ E\left( {\tilde{\delta }_{i}^{ - } } \right) = \sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) $$

(13)

$$ E\left( {\tilde{\delta }_{i}^{ + } } \right) = \sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) + \sigma_{i} \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) $$

(14)

where ${\varvec{L}}\left( . \right)$ denotes the loss function.³ The proof of (13) and (14) can be found in Appendix II and Appendix III. Therefore Program (10) is transformed into:

$$ \begin{aligned} & Min \mathop \sum \limits_{i = 1}^{I} \left[ {w_{i}^{ + } {\varvec{E}}\left( {\tilde{\delta }_{i}^{ + } } \right) + w_{i}^{ - } {\varvec{E}}\left( {\tilde{\delta }_{i}^{ - } } \right)} \right] \\ & s.t.\,\sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - E\left( {\tilde{\delta }_{i}^{ - } } \right) = 0 \\ & \quad \quad \sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) + \sigma_{i} \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - E\left( {\tilde{\delta }_{i}^{ + } } \right) = 0 \\ & \quad \quad i = 1,2, \ldots , I \\ \end{aligned} $$

(15)

The model outlined above has a limitation in that it concentrates solely on optimizing solutions, rather than maximizing the decision maker's satisfaction by incorporating their preferences, as advocated by Schultz et al. (2010). This poses a noteworthy concern because as the achievement level approaches the optimal point, marginal satisfaction often decreases. As a result, this limitation could lead to a solution that fails to maximize the decision maker's overall satisfaction. To address this limitation, we include satisfaction functions into the model. Consequently, Program (15) can be written as:

$$ \begin{aligned} & Max \mathop \sum \limits_{i = 1}^{I} \left[ {w_{i}^{ + } {\varvec{S}}_{{\varvec{i}}} \left( {E\left( {\tilde{\delta }_{i}^{ + } } \right)} \right) + w_{i}^{ - } {\varvec{S}}_{{\varvec{i}}} \left( {E\left( {\tilde{\delta }_{i}^{ - } } \right)} \right)} \right] \\ & s.t.\,\sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - E\left( {\tilde{\delta }_{i}^{ - } } \right) = 0 \\ & \quad \quad \sigma_{i} {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) + \sigma_{i} \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - E\left( {\tilde{\delta }_{i}^{ + } } \right) = 0 \\ & \quad \quad i = 1,2, \ldots , I \\ \end{aligned} $$

(16)

where ${\varvec{S}}_{{\varvec{i}}} \left( . \right)$ is the satisfaction function for objective $i$ with the thresholds presented in Fig. 1, and ${\varvec{S}}_{{\varvec{i}}} \left( {E\left( {\tilde{\delta }_{i}^{ + } } \right)} \right)$ and ${\varvec{S}}_{{\varvec{i}}} \left( {E\left( {\tilde{\delta }_{i}^{ - } } \right)} \right)$ represent the satisfaction levels associated with the expected deviations for goal $i$. It is evident that when the satisfaction functions exhibit a strictly increasing pattern, the resulting solution will be Pareto optimal.

The establishment of satisfaction thresholds can be a complex task, especially when dealing with uncertainty. One potential strategy to simplify this process is the adoption of a unified satisfaction function for all goals. Typically, three key goal-specific factors necessitate distinct satisfaction thresholds: goal magnitude, goal uncertainty, and goal importance (preference). Generally, decision makers set tighter satisfaction thresholds for goals with smaller magnitudes, less uncertainty, or higher levels of importance. However, the relative importance of the goals can be managed through their respective weights, thanks to the weighting mechanism integrated into the achievement function. This eliminates the need to consider ‘goal importance’ in the determination of satisfaction thresholds. Additionally, normalizing expected deviations relative to the standard deviations of the goals can effectively neutralize the influence of goal magnitude and uncertainty. This process ensures that the thresholds are dimensionless and independent of the uncertainty associated with each goal, allowing for the application of a unified satisfaction function across all goals. Therefore, we can rewrite program (16) as:

$$ \begin{aligned} & Max \mathop \sum \limits_{i = 1}^{I} \left( {w_{i}^{ + } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{i}^{ + } } \right)}}{{\sigma_{i} }}} \right) + w_{i}^{ - } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{i}^{ - } } \right)}}{{\sigma_{i} }}} \right)} \right) \\ & s.t. {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - \frac{{ E\left( {\tilde{\delta }_{i}^{ - } } \right)}}{{\sigma_{i} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) + \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} a_{ij} x_{j} - \mu_{i} }}{{\sigma_{i} }}} \right) - \frac{{E\left( {\tilde{\delta }_{i}^{ + } } \right)}}{{\sigma_{i} }} = 0 \\ & \quad \quad i = 1,2, \ldots , I \\ \end{aligned} $$

(17)

where ${\varvec{S}}$(.) denotes a unified satisfaction function defined as a function of normalized deviation.⁴

4 MIEOQ problems formulation

In this section, we present the general formulation of a MIEOQ problem with stochastic goals and independent lot orders and deliveries When only demands are stochastic with known means $\left( {D_{j} } \right)$ and standard deviations over lead time $\left( {\sigma_{j} } \right)$, the objective is to find the order quantities $\left( {Q_{j} } \right)$, order frequency $\left( {N_{j} } \right)$, and safety stock levels $\left( {ss_{j} } \right)$ that minimize the expected inventory cost. Safety stock is a certain quantity of inventory held in addition to the expected demand over lead-time. The expected inventory cost consists of carrying costs, ordering costs, and stock-out costs of all items. So, the inventory problem can be formulated as follows:

$$ \begin{aligned} & Min \mathop \sum \limits_{j = 1}^{n} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)H_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) \\ & s.t.\,f_{i} \left( {Q,N,ss} \right) \le g_{i} \\ & \quad \quad i = 1,2, \ldots ,I \\ \end{aligned} $$

(18)

where $f_{i} \left( {Q,V,ss} \right) \le g_{i}$ denotes constraint $i$ as a function of $Q$, N and $ss$ which are the vectors of order quantity, order frequency, and safety stock variables. $g_{i}$ is the right-hand side (RHS) of constraint $i$, $I$ is the number of the constraints, and $n$ is the number of the items. The carrying cost of item $j$ equals $\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)h_{j} C_{j}$, where $\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)$ is the average inventory and $h_{j} C_{j}$ denotes the annual holding cost per unit for item $j$. The ordering cost is formulated as $N_{j} S_{j}$, where $N_{j}$ represents the expected order frequency and $S_{j}$ denotes the cost per order for item $j$. The expected stockout cost when demand during stockout is backlogged, as provided by Chopra (2019), equals $N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j}$, in which $B_{j}$ represents the backlog cost per unit, and $\sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)$ is the expected backlog for item $j$ where ${\varvec{L}}\left( . \right)$ denotes the loss function.

The shift from a scenario with stochastic demand alone to one where resources also introduce uncertainty, indeed emphasizes the necessity of a robust approach. Stochastic goal programming (SGP) stands out as a favorable choice due to its ability to handle and adapt to uncertainty, showcasing the distinguished feature of robustness. In the context of inventory management, robustness refers to the approach's ability to adapt and perform effectively in achieving specified goals and meeting constraints, even when faced with unpredictable changes in demand patterns, budget constraints, or resource availability. The solution of a robust approach remains effective and viable across a variety of potential scenarios, providing stability and consistency in performance despite the uncertainties and variations in the system. Using the SGP model, the SGP model of an MIEOQ problem with stochastic objectives and constraints can be written as:

$$ \begin{aligned} & Min w_{c}^{ + } \tilde{\delta }_{c}^{ + } + w_{c}^{ - } \tilde{\delta }_{c}^{ - } + \mathop \sum \limits_{i = 1}^{I} w_{i}^{ + } \tilde{\delta }_{i}^{ + } + w_{i}^{ - } \tilde{\delta }_{i}^{ - } \\ & s.t.\,\mathop \sum \limits_{j = 1}^{n} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)H_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \tilde{\delta }_{c}^{ + } + \tilde{\delta }_{c}^{ - } = \tilde{g}_{c} \\ & \quad \quad f_{i} \left( {Q,N,ss} \right) - \tilde{\delta }_{i}^{ + } + \tilde{\delta }_{i}^{ - } = \tilde{g}_{i} \\ & \quad \quad i = 1,2, \ldots ,I \\ \end{aligned} $$

(19)

where $\tilde{g}_{c}$ is the stochastic goal for the inventory-cost objective, $\tilde{g}_{i}$ represents the goal for the rest of objectives, and $\tilde{\delta }_{c}^{ + }$, $\tilde{\delta }_{c}^{ - }$, $\tilde{\delta }_{i}^{ + }$, and $\tilde{\delta }_{i}^{ - }$ refer to the stochastic deviation variables. To address the challenge of goal setting when goals are stochastic, we use the AFGP model and integrate it with the unified satisfaction function concept to explicitly incorporate the decision-maker’s preference into the model. Therefore program (19) can be written as:

$$ \begin{aligned} & Max w_{c}^{ + } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{c}^{ + } } \right)}}{{\sigma_{c} }}} \right) + w_{c}^{ - } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{c}^{ - } } \right)}}{{\sigma_{c} }}} \right) + \mathop \sum \limits_{i = 1}^{I} w_{i}^{ + } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{i}^{ + } } \right)}}{{\sigma_{i} }}} \right) + w_{i}^{ - } {\varvec{S}}\left( {\frac{{E\left( {\tilde{\delta }_{i}^{ - } } \right)}}{{\sigma_{i} }}} \right) \\ & s.t.\,{\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)H_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \mu_{c} }}{{\sigma_{c} }}} \right) - \frac{{E\left( {\tilde{\delta }_{c}^{ - } } \right)}}{{\sigma_{c} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)H_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \mu_{c} }}{{\sigma_{c} }}} \right)\\ &\quad+ \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)H_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \mu_{c} }}{{\sigma_{c} }}} \right) - \frac{{E\left( {\tilde{\delta }_{c}^{ + } } \right)}}{{\sigma_{c} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{f_{i} \left( {Q,N, ss} \right) - \mu_{i} }}{{\sigma_{i} }}} \right) - \frac{{E\left( {\tilde{\delta }_{i}^{ - } } \right)}}{{\sigma_{i} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{f_{i} \left( {Q,N, ss} \right) - \mu_{i} }}{{\sigma_{i} }}} \right) + \left( {\frac{{f_{i} \left( {Q,N, ss} \right) - \mu_{i} }}{{\sigma_{i} }}} \right) - \frac{{E\left( {\tilde{\delta }_{i}^{ + } } \right)}}{{\sigma_{i} }} = 0 \\ & \quad \quad i = 1,2, \ldots ,I \\ \end{aligned} $$

(20)

where $E\left( {\tilde{\delta }_{c}^{ + } } \right)$, $E\left( {\tilde{\delta }_{c}^{ - } } \right)$, $E\left( {\tilde{\delta }_{i}^{ + } } \right)$, and $E\left( {\tilde{\delta }_{i}^{ - } } \right)$ are the expected values of the deviations, and $S\left( . \right)$ denotes the unified satisfaction function.

In the next section, we present an illustrative example to clarify our introduced approach, providing a deeper understanding of how it operates in practice.

5 Illustrative example

A category manager at an electronics and appliance store needs to determine the optimal order quantity and safety stock for four products, each subject to random demand. The objective is to satisfy the demands within the budget and handling time constraints while achieving satisfactory levels of turnover and fill rate, with all goals deemed equally important. The products are replenished independently, and all random goals are assumed to be normally distributed. The products’ metrics are provided in Table 1.

Table 1 Product metrics

Due to demand uncertainty and budget allocation among several product categories, the category manager expects the annual inventory budget to be approximately $100,000, with a standard deviation of $10,000. The annual carrying cost per unit is 3% of the unit cost, and the cost per order is $2,200. Variations in receiving staff assignments result in random handling times, with an average of 700 min and a standard deviation of 70 min.

The market is highly sensitive to product availability and delays often lead to customers switching to competitors. Hence, maintaining a high service level is crucial. Market research indicates that competitors achieve an average service level of 85% with a standard deviation of 5%. To promote efficiency, every year the store rewards category managers who can achieve the highest inventory turnover. In the previous years, the average inventory turnover across categories was 15 times with a standard deviation of 2.

Analysis:

The deterministic model of this example can be formulated as follows. The variables’ notations and explanations are provided in Table 2.

$$ \begin{aligned} & Min \mathop \sum \limits_{j = 1}^{4} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)h_{j} C_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) \\ & s.t.\,N_{j} Q_{j} \ge D_{j} { } \\ & \quad \quad \frac{{\mathop \sum \nolimits_{j = 1}^{n} \left( {N_{j} Q_{j} C_{j} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)C_{j} }} \ge U \\ &\quad \quad \mathop \sum \limits_{j = 1}^{n} \left( {Q_{j} t_{j} } \right) \le T \\ &\quad \quad {\varvec{F}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right) \ge sl_{j} \\ &\quad \quad j = 1,2,3,4 \\ \end{aligned} $$

(21)

Table 2 Variable notations and descriptions

As shown in program (18), the objective cost function consists of carrying costs, ordering costs, and stockout costs represented by $\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)h_{j} C_{j}$, $N_{j} S_{j}$, and $N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j}$, respectively. The first constraint in program (21) ensures that $N_{j} Q_{j}$, the total units ordered for item $j$, is greater than or equal to the expected demand, $D_{j}$. The second constraint requires the aggregate inventory turnover to be greater than or equal to the required level $U$. The aggregate inventory turnover equals the cost of goods sold, $\mathop \sum \nolimits_{j = 1}^{n} \left( {N_{j} Q_{j} C_{j} } \right)$, divided by the inventory cost, $\mathop \sum \nolimits_{j = 1}^{n} \left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)C_{j}$. The third constraint limits the required handling time, $\mathop \sum \nolimits_{j = 1}^{4} \left( {Q_{j} t_{j} } \right)$, to the available time $T$. Finally, constraint four requires the service level for item $j$, represented by ${\varvec{F}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)$, to be greater than or equal to the desired level $sl_{j}$, where ${\varvec{F}}\left( . \right)$ denotes the cumulative distribution function.

Based on the above deterministic model, the SGP model of the problem can be written as:

$$ \begin{aligned} & Min w_{c}^{ + } \tilde{\delta }_{c}^{ + } + \mathop \sum \limits_{j = 1}^{4} w_{{D_{j} }}^{ - } \tilde{\delta }_{{D_{j} }}^{ - } + w_{u}^{ - } \tilde{\delta }_{u}^{ - } + w_{t}^{ + } \tilde{\delta }_{t}^{ + } + \mathop \sum \limits_{j = 1}^{4} w_{{sl_{j} }}^{ - } \tilde{\delta }_{{sl_{j} }}^{ - } \\ & s.t.\,\mathop \sum \limits_{j = 1}^{4} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)h_{j} C_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \tilde{\delta }_{c}^{ + } + \tilde{\delta }_{c}^{ - } = \tilde{g}_{c} \\ & \quad \quad N_{j} Q_{j} - \tilde{\delta }_{{D_{j} }}^{ + } + \tilde{\delta }_{{D_{j} }}^{ - } = \tilde{g}_{{D_{j} }} \\ & \quad \quad \frac{{\mathop \sum \nolimits_{j = 1}^{n} \left( {NQ_{j} C_{j} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{n} \left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)C_{j} }} - \tilde{\delta }_{u}^{ + } + \tilde{\delta }_{u}^{ - } = \tilde{g}_{u} \\ & \quad \quad \mathop \sum \limits_{j = 1}^{4} \left( {Q_{j} t_{j} } \right) - \tilde{\delta }_{t}^{ + } + \tilde{\delta }_{t}^{ - } = \tilde{g}_{t} \\ & \quad \quad F\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right) - \tilde{\delta }_{{sl_{j} }}^{ + } + \tilde{\delta }_{{sl_{j} }}^{ - } = \tilde{g}_{{sl_{j} }} \\ & \quad \quad j = 1,2,3,4 \\ \end{aligned} $$

(22)

where $\tilde{g}_{c}$, $\tilde{g}_{{D_{j} }}$, $\tilde{g}_{u}$, $\tilde{g}_{t}$, and $\tilde{g}_{{sl_{j} }}$ are stochastic goals.

Finally, employing the AFGP approach and incorporating the concept of satisfaction function, we can formulate the SGP model of the problem as:

$$ \begin{aligned} & Max w_{c}^{ + } S\left( {\frac{{E\left( {\tilde{\delta }_{c}^{ + } } \right)}}{{\sigma_{c} }}} \right) + \mathop \sum \limits_{j = 1}^{4} w_{{D_{j} }}^{ - } S\left( {\frac{{E\left( {\tilde{\delta }_{{D_{j} }}^{ - } } \right)}}{{\sigma_{{D_{j} }} }}} \right) + w_{u}^{ - } S\left( {\frac{{E\left( {\tilde{\delta }_{u}^{ - } } \right)}}{{\sigma_{u} }}} \right) + w_{t}^{ + } S\left( {\frac{{E\left( {\tilde{\delta }_{t}^{ + } } \right)}}{{\sigma_{t} }}} \right)\\ &\quad+ \mathop \sum \limits_{j = 1}^{4} w_{{sl_{j} }}^{ - } S\left( {\frac{{E\left( {\tilde{\delta }_{{sl_{j} }}^{ - } } \right)}}{{\sigma_{{sl_{j} }} }}} \right) \\ & s.t.\,{\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{4} \left( {\left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)h_{j} C_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \mu_{c} }}{{\sigma_{c} }}} \right)\\ &\quad+ \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{4} \left( {\frac{{Q_{j} }}{2}h_{j} C_{j} + N_{j} S_{j} + N_{j} \sigma_{j} {\varvec{L}}\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right)B_{j} } \right) - \mu_{c} }}{{\sigma_{c} }}} \right) - \frac{{E\left( {\tilde{\delta }_{c}^{ + } } \right)}}{{\sigma_{c} }} = 0 \\ & \quad \quad \user2{ L}\left( {\frac{{N_{j} Q_{j} - \mu_{{D_{j} }} }}{{\sigma_{{D_{j} }} }}} \right){ } - \frac{{E\left( {\tilde{\delta }_{{D_{j} }}^{ - } } \right)}}{{\sigma_{{D_{j} }} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{4} \left( {NQ_{j} C_{j} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{4} \left( {\frac{{Q_{j} }}{2} + ss_{j} } \right)C_{j} }} - \mu_{u} } \right)/\sigma_{u} } \right) - \frac{{E\left( {\tilde{\delta }_{u}^{ - } } \right)}}{{\sigma_{u} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{4} \left( {Q_{j} t_{j} } \right) - \mu_{t} }}{{\sigma_{t} }}} \right) + \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{4} \left( {Q_{j} t_{j} } \right) - \mu_{t} }}{{\sigma_{t} }}} \right) - \frac{{E\left( {\tilde{\delta }_{t}^{ + } } \right)}}{{{ }\sigma_{t} }} = 0 \\ & \quad \quad {\varvec{L}}\left( {\frac{{F\left( {\frac{{ss_{j} }}{{\sigma_{j} }}} \right) - \mu_{{sl_{j} }} }}{{\sigma_{{sl_{j} }} }}} \right){ } - \frac{{E\left( {\tilde{\delta }_{{sl_{j} }}^{ - } } \right)}}{{\sigma_{{sl_{j} }} }} = 0 \\ \end{aligned} $$

(23)

To solve this problem, the decision-maker can adopt an initial satisfaction function that appears suitable and then refine it based on the results to better align with their preferences. Let’s assume that the decision-maker starts with satisfaction function A, with veto, nil, and indifferent thresholds of 1, 0.5, and 0, respectively.

Solving the problem with function A results in a satisfaction level of 54%, accompanied by multiple deviations equal to the veto threshold. This suggests that function A’s thresholds are overly restrictive and need to be relaxed. One viable adjustment is to raise the nil threshold from 0.5 to, for example, 0.8, as illustrated in function B. This adjustment allows for greater tolerance and prevents a premature shift to other goals, as the decision-maker is more willing to find satisfaction in achieving outcomes somewhat farther from the ideal goal.

Upon resolving the problem using function B, the satisfaction level improves slightly reaching 57%. However, some deviations persist at the veto threshold, signaling that the thresholds remain restrictive, necessitating further adjustments.

To further ease the thresholds, the decision-maker can increase the nil threshold further or introduce a transition threshold $\left( {\alpha_{t} } \right)$ as demonstrated by function C. In this function, the satisfaction rate decreases from 3 to 0.5 at a transition threshold of 0.2, indicating a deliberate shift in focus towards more attainable objectives. As indicated in Table 3, adopting function C leads to a substantial increase in the satisfaction level to 93%, accompanied by deviations well below the nil threshold of 0.5.

Table 3 Comparison of the solutions for the illustrative example

In the scenario where the decision-maker simultaneously increases the nil and transition thresholds, depicted in function D, the satisfaction level experiences a modest improvement to 95%. Although this results in a slight deterioration in the achieved deviations, they still remain well below the nil threshold.

Increasing the transition threshold further from 0.2 to 0.5, as illustrated in function E, elevates the satisfaction level to 99%. However, this adjustment comes with a trade-off, resulting in an increase in the achieved deviation for the cost objective, from 0.36 to 0.5. On the flip side, deviations for all other objectives decrease. This contrasting change in achieved deviations leads to a less balanced outcome compared to functions C and D. Given the decision-maker's equal consideration of all objectives, this imbalance may not align with their preferences. Consequently, the decision-maker might favor functions C and D over function E, as they offer a more balanced solution across all objectives.

This example not only demonstrates the effectiveness of the proposed approach in guiding the decision-maker towards a balanced and satisfactory solution but also emphasizes the critical role of iterative adjustments to satisfaction thresholds. Through this iterative process, the decision-maker engages in a dynamic exploration of the optimal solution landscape, allowing for a comprehensive assessment of the trade-offs associated with each adjustment.

Furthermore, the example highlights the systematic and adaptive nature of the proposed approach. It empowers the decision-maker to navigate the intricate landscape of satisfaction thresholds, ensuring that the final solution not only meets satisfaction criteria but also aligns with their overarching preferences across multiple objectives. This alignment is facilitated by a nuanced representation of preferences within the satisfaction function, which incorporates a dynamic weighting mechanism. Beyond simply assessing goal attainment, this mechanism adjusts goal weights based on the diminishing effect of satisfaction, recognizing the changing importance of goals as they approach ideal levels. This flexibility in modeling goal significance not only addresses concerns about oversimplification but also enhances the model's capacity to reflect trade-offs in decision-making under uncertain conditions.

6 Concluding remarks

This study effectively navigates the complex landscape of multi-item economic order quantity (MIEOQ) problems, tackling three interconnected challenges. Firstly, existing models in this domain often fall short in explicitly incorporating decision-makers' preferences within the solution framework, especially in uncertain conditions. Secondly, current stochastic goal programming (SGP) approaches grapple with the complexity of effective goal setting. Lastly, the use of distinct satisfaction functions for each uncertain goal, while common, can complicate the threshold-setting process, undermining their effectiveness.

To overcome these challenges, we propose an innovative integration of a new SGP approach, named aspiration-free goal programming (AFGP), with a unified satisfaction function. AFGP operates by minimizing the sum of expected values of deviation variables, eliminating the need for specific goals or aspiration levels. This methodology offers a versatile, preference-sensitive framework for solving MIEOQ problems, ensuring a Pareto optimal solution. The focus on expected deviations under uncertain goal conditions facilitates nuanced decision-making, accommodating the stochastic nature of original goal distributions.

The pivotal role of a unified satisfaction function cannot be overstated in our approach. By providing a common measure of satisfaction across all goals, it simplifies the decision-making process. While setting satisfaction thresholds can be complex, especially in uncertainty, adopting a unified satisfaction function proves to be a potential strategy to streamline this intricate process.

To illustrate the practicality and efficacy of our proposed approach, we present a detailed illustrative example. This example serves as more than just an application—it acts as a tangible demonstration of how our approach addresses the specific challenges within MIEOQ. Through the step-by-step implementation of AFGP in uncertain conditions, readers witness firsthand the resolution of challenges related to preference incorporation and goal setting.

Acknowledging concerns that minimizing the sum of expected values of deviation variables could oversimplify complexities, it is crucial to recognize that AFGP intentionally embraces simplicity for enhanced practical applicability. This deliberate choice strikes a balance between simplicity and accuracy, ensuring real-world relevance.

While our illustrative example showcases the application within a specific context, it's paramount to emphasize the generalizability of our proposed approach. The integration of AFGP with a unified satisfaction function offers a systematic and adaptive framework applicable to a broader range of MIEOQ problems and potentially extends its utility to other decision-making domains.

In summary, our study contributes significantly to the MIEOQ literature by introducing an innovative solution to long-standing challenges. Through AFGP and a unified satisfaction function, we bridge gaps in preference incorporation, goal setting, and complexity. The adaptability of our approach ensures a nuanced decision-making process even in uncertain environments.

As we conclude, the integrated AFGP and unified satisfaction function emerge not only as a solution to specific MIEOQ challenges but as a testament to the broader potential of this approach in advancing decision-making methodologies under uncertainty. This work paves the way for future research to explore and refine these methodologies, ensuring continued progress in the field of Multi-Item Economic Order Quantity problems.

Appendices

Appendices

Appendix I: An intermediate evaluation

$$ \begin{gathered} A = \mathop \int \limits_{x = - \infty }^{a} xf\left( x \right)dx = \mathop \int \limits_{x = - \infty }^{a} x\frac{1}{{\sqrt {2\pi } \sigma }}e^{{ - \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} dx \hfill \\ After substituting z = \frac{{\left( {x - \mu } \right)}}{\sigma }and dx = \sigma dz we have \hfill \\ A = \mathop \int \limits_{z = - \infty }^{{\frac{a - \mu }{\sigma }}} \frac{{\left( {z\sigma + \mu } \right)}}{{\sqrt {2\pi } }}e^{{ - \frac{{z^{2} }}{2}}} dz = \mu \mathop \int \limits_{z = - \infty }^{{\frac{a - \mu }{\sigma }}} \frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{{z^{2} }}{2}}} dz + \sigma \mathop \int \limits_{z = - \infty }^{{\frac{a - \mu }{\sigma }}} z\frac{1}{{\sqrt {2\pi } }}e^{{ - \frac{{z^{2} }}{2}}} dz \hfill \\ A = \mu F_{s} \left[ {\frac{a - \mu }{\sigma }} \right] - \sigma f_{s} \left[ {\frac{a - \mu }{\sigma }} \right] \hfill \\ \end{gathered} $$

Appendix II:

Expected negative deviation between achievement level and goal.

If O denotes the achievement level and x represent the goal, negative deviation results only if x > O. We thus have

$$ \begin{aligned} E\left( {\tilde{\delta }^{ - } } \right) & = \mathop \int \limits_{x = O}^{\infty } \left( {x - O} \right)f\left( x \right)dx = \mathop \int \limits_{x = O}^{\infty } xf\left( x \right)dx - \mathop \int \limits_{x = O}^{\infty } Of\left( x \right)dx \\ & = \mathop \int \limits_{x = - \infty }^{\infty } xf\left( x \right)dx - \mathop \int \limits_{x = - \infty }^{O} xf\left( x \right)dx - O\left\{ {1 - F_{s} \left( {\frac{O - \mu }{\sigma }} \right)} \right\} \\ & = \left( {\mu - O} \right) + OF_{s} \left( {\frac{O - \mu }{\sigma }} \right) - \mathop \int \limits_{x = - \infty }^{O} xf\left( x \right)dx \\ \end{aligned} $$

$$ Using\,the\,result\,of\,Appendix\,I\,we\,obtain: $$

$$ \begin{aligned} E\left( {\tilde{\delta }^{ - } } \right) & = \left( {\mu - O} \right) + OF_{s} \left( {\frac{O - \mu }{\sigma }} \right) - \mu F_{s} \left( {\frac{O - \mu }{\sigma }} \right) + \sigma f_{s} \left( {\frac{O - \mu }{\sigma }} \right) \\ & = \sigma \left\{ { - \left( {\frac{O - \mu }{\sigma }} \right)\left\{ {1 - F_{s} \left( {\frac{O - \mu }{\sigma }} \right)} \right\} + f_{s} \left( {\frac{O - \mu }{\sigma }} \right)} \right\} \\ \end{aligned} $$

$$ Therefore $$

$$ E\left( {\tilde{\delta }^{ - } } \right) = \sigma L\left( {\frac{O - \mu }{\sigma }} \right) $$

$where\,L\left( . \right)\,is\,standard\,loss\,function$

Appendix III:

Expected positive deviation between achievement level and goal.

If O denotes the achievement level and x represent the goal, positive deviation results only if x < O. We thus have

$$ \begin{aligned} E\left( {\tilde{\delta }^{ + } } \right) & = \mathop \int \limits_{x = - \infty }^{O} \left( {O - x} \right)f\left( x \right)dx = \mathop \int \limits_{x = - \infty }^{O} Of\left( x \right)dx - \mathop \int \limits_{x = - \infty }^{O} xf\left( x \right)dx \\ & = OF_{s} \left( {\frac{O - \mu }{\sigma }} \right) - \mathop \int \limits_{x = - \infty }^{O} xf\left( x \right)dx \\ \end{aligned} $$

$$ Using\,the\,result\,of\,Appendix\,I,\,we\,obtain: $$

$$ \begin{aligned} E\left( {\tilde{\delta }^{ + } } \right) & = OF_{s} \left( {\frac{O - \mu }{\sigma }} \right) - \mu F_{s} \left( {\frac{O - \mu }{\sigma }} \right) + \sigma f_{s} \left( {\frac{O - \mu }{\sigma }} \right) \\ & = \left( {O - \mu } \right)F_{s} \left( {\frac{O - \mu }{\sigma }} \right) + \sigma f_{s} \left( {\frac{O - \mu }{\sigma }} \right) \\ & = \sigma \left\{ {\left( {\frac{O - \mu }{\sigma }} \right)F_{s} \left( {\frac{O - \mu }{\sigma }} \right) + f_{s} \left( {\frac{O - \mu }{\sigma }} \right)} \right\} \\ \end{aligned} $$

$$ Therefore $$

$$ E\left( {\tilde{\delta }^{ + } } \right) = \sigma L\left( {\frac{O - \mu }{\sigma }} \right) + \sigma \left( {\frac{O - \mu }{\sigma }} \right) $$

$where\,L\left( . \right)\,is\,standard\,loss\,function$