A novel integration of MCDM methods and Bayesian networks: the case of incomplete expert knowledge

Abstract

In this study, we propose an effective integration of multi criteria decision making methods and Bayesian networks (BN) that incorporates expert knowledge. The novelty of this approach is that it provides decision support in case the experts have partial knowledge. We use decision-making trial and evaluation laboratory (DEMATEL) to elicit the causal graph of the BN based on the causal knowledge of the experts. BN provides the evaluation of alternatives based on the decision criteria which make up the initial decision matrix of the technique for order of preference by similarity to the ideal solution (TOPSIS). We then parameterize BN using Ranked Nodes which allows the experts to submit their knowledge with linguistic expressions. We propose the analytical hierarchy process to determine the weights of the decision criteria and TOPSIS to rank the alternatives. A supplier selection case study is conducted to illustrate the effectiveness of the proposed approach. Two evaluation measures, namely, the number of mismatches and the distance due to the mismatch are developed to assess the performance of the proposed approach. A scenario analysis with 5% to 20% of missing values with an increment of 5% is conducted to demonstrate that our approach remains robust as the level of missing values increases.

1 Introduction and problem definition

In many logistical problems such as the supplier selection problem, data is not always readily available or is often rather limited. For instance, when new supplier performance about some criteria cannot be known determined and some sellers may not want to share all information or spend their own resources on gathering information sought by buyers. One way forward is for the decision makers to take advantage of the experts’ knowledge and perception in such circumstances. The buyer may be able to gather data about some criteria, such as price and reputation through market research. On the other hand, the buyer may form a judgement about some criteria like cooperation and communication abilities based on the purchasing interviews. In addition, a buyer may ask for sample parts which can be used to evaluate the suppliers in terms of product quality, delivery performance, among others. Note that it is not possible to gain knowledge about the supplier performance based on the sample parts, such as reliability and price stability. Our aim is to develop a robust approach which takes into account incomplete expert knowledge. We believe this approach is important for effective decision making with expert knowledge even if it is incomplete. There are some multi criteria decision making methods (MCDM) that consider expert knowledge (Zhang et al., 2017; Chowdhury & Paul, 2020). However, these are often deterministic methods that are not designed to deal with uncertainty. Our approach deals with uncertainty with probabilistic estimations.

One philosophy is that experts are encouraged to submit their knowledge quantitatively although they may feel more comfortable providing such information qualitatively. The tendency of a qualitative submission and the uncertainty in expert knowledge prompt to integrate MCDMs with fuzzy approach (Zeshui & Zhang, 2022, Ecer, 2020, Mohammed, 2020a). There is a lot of research on fuzzy approaches as will be shown in the literature review. In this paper, we propose to use Ranked Nodes to model qualitative judgements of experts in Bayesian networks (BNs) which will be briefly reviewed in the next section.

BNs have the flexibility to work even if there is incomplete knowledge. This is usually achieved by estimating the missing knowledge based on the causal relationship between the criteria. This can be considered as a dynamic evaluation tool. In other words, when a decision maker has a new evidence about a given criterion, BNs update the entries of the network based on the entered evidence as posterior probabilities. This demonstrates that BNs are effective tools to evaluate the alternatives based on the causal relationship between the selection criteria. However, it is worth stressing that there is no systematic way of determining the causal structure of BNs. Kaya and Yet (2019) adopted DEMATEL to resolve this issue. They determined the causal relationship between the criteria based on DEMATEL and then parameterized the BN with Ranked Nodes systematically. In this network, the buyer can evaluate alternative suppliers based on each criterion. However, it is worth noting that the network does not rank the alternatives based on the overall performance. In this study, we propose to extend the work of Kaya and Yet (2019) by producing a ranking of the suppliers. To achieve this, we incorporate TOPSIS into our methodology.

TOPSIS is one of the commonly used MCDM methods for the supplier selection problem. Inputs of TOPSIS are weights of the criteria and the evaluation matrix of the alternatives based on the criteria. In case there is a lack of data, the evaluation of the alternatives based on criteria is carried out on a scale that needs to be determined. Mostly, as experts prefer to submit their knowledge by linguistic expressions, a fuzzy-based approach is usually integrated with TOPSIS (Nilashi et al., 2019; Venkatesh et al., 2019). As the full expert knowledge is not always possible, BN provides a full probabilistic evaluation matrix for TOPSIS based on the expert knowledge which is submitted with linguistic expressions. The missing knowledge is incorporated based on the causal relationship between the criteria which then provides a complete and an updated evaluation matrix.

Another critical input of TOPSIS is the weights of the decision criteria. It is hard to elicit these weights quantitatively. Liu and Wan (2019) use ELECTRE I and III for the weights of criteria. One way forward, which is commonly adopted in the literature, is to integrate AHP with TOPSIS for the elicitation of the weights (Jain et al., 2018; Mohammed et al., 2019b; Akgün & Erdal, H., 2019).

In summary, we rank the suppliers with TOPSIS. Weights of the criteria are determined by AHP. Initial decision matrix of TOPSIS is elicited by BN. Causal graphical structure and parameterization of the BN is done with DEMATEL.

The motivation and the contributions of the study are summarized in the following two paragraphs, namely, (a) and (b)

(a) Motivation

When data is not available, expert knowledge is a valuable alternative source for decision making. However, sometimes even full expert knowledge is not available. Our motivation comes from decision making in case of incomplete knowledge. For this purpose we need a tool which is able to fill the missing parts in a reliable way. BNs are causal probabilistic networks. They are able to make reliable estimations based on the available information according to cause-effect relationship between the decision criteria. In addition, when a new information obtained about any criterion, the BN updates the network based on this new information. Another challenge when making decision with expert knowledge is elicitation of expert knowledge as the experts tend to submit their knowledge qualitatively. The Ranked Nodes tool of Bayesian Networks offers submission of expert knowledge in a qualitative ordinal scale as "low","medium" and "high". BN turns them into quantitative numbers while considering causal relations between the criteria. These results provide us to see the performance of each alternative based on each decision criterion dynamically and also produces the initial decision matrix for ranking the alternatives by TOPSIS. In this study, we therefore propose a systematic solution approach for decision making with incomplete expert knowledge by taking advantage of the strengths of the methods which are used in the proposed approach.

(b) Contributions

• (i) An effective integration of MCDM methods and BNs for multi criteria decision problems is proposed.

• (ii) This novel approach is able to work with both complete and incomplete expert knowledge.

• (iii) This approach is able to deal with uncertainty by making reliable probabilistic estimations.

• (iv) This approach considers causal relationship between the decision criteria and updates the network based on any change arising from any of the criteria.

• (v) Ranked Nodes are used for easy elicitation of probabilities of BN based on qualitative judgements of experts.

• (vi) The value of the knowledge is analysed and a scenario analysis is conducted with interesting results.

The rest of the paper is organised as follows. A short literature review related to MCDM, BN and integrated approaches is given in the next section. The techniques that are used in this study are outlined in Sect. 3 followed by the proposed approach in Sect. 4. An illustrative example using a case study is provided in Sect. 5 and a scenario analysis is presented in Sect. 6. Our conclusion and suggestions are provided in the final section. An appendix that briefly covers AHP, TOPSIS and DEMATEL is also given for completeness.

2 Literature review

As we aim to integrate MCDM methods and BNs for decision making with incomplete expert knowledge, we organize this section into three subsections. We first present a short literature review on MCDM methods with a focus on those that are used in this study, namely, AHP, TOPSIS and DEMATEL, though other related multi-criteria decision making problems will also be briefly presented. This is followed by a short introduction on BNs. As we conducted the case study for the supplier selection problem, the final subsection will cover and discuss the integration of those chosen MCDM methods and BN while highlighting our contribution.

2.1 A short literature review of MCDM

MCDM methods are commonly used for decision making with expert knowledge. Most of the time, due to unavailability of data, the researchers tend to rely on expert knowledge for the supplier selection problem. Therefore, MCDM methods are commonly used methods for the supplier selection problem. As AHP, TOPSIS and DEMATEL are used in our study, we mainly focus on reviewing these approaches.

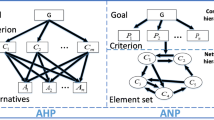
AHP is one of the commonly used MCDM methods particularly for the supplier selection problem (Çalık, 2021; Ecer, 2020). It works based on the pairwise comparison of criteria and alternatives (Liu et al., 2020). As experts prefer to submit the relative preferences between criteria and alternatives by linguistic values, hybridization of AHP with fuzzy logic is common for supplier selection problem (Ho et al., 2021; Ecer, 2020). Analytic network process(ANP) is an MCDM method which works in reverse hierarchy. Aguezzoul (2014) for instance use this approach for the selection of 3PL providers.

TOPSIS is another commonly used MCDM method for the supplier selection problem. It works based on distance to the ideal solution, see Wang et al. (2009); Mohammed (2020a). Fuzzy hybridization is also common with TOPSIS (Nilashi et al., 2019; Venkatesh et al., 2019; Memari et al., 2019).

Rodrigues et al. (2014) compares TOPSIS and AHP methods for the supplier selection problem in terms of adequacy to changes of alternatives or criteria, agility in the decision process, computational complexity, adequacy to support group decision making, the number of alternative suppliers and criteria and also modelling of uncertainty. The results also show that TOPSIS is more robust in the case of change of alternatives or criteria besides being more effective in terms of computational time. In other words, TOPSIS is more practical in terms of the number of criteria, alternatives and decision makers. In addition, TOPSIS has the agility in decision compared to AHP that has a hierarchical structure resulting in processing pairwise comparison at each level.

VIKOR is an MCDM approach which is similar to TOPSIS. It works based on the maximum utility and minimum regret of the decision makers. Wu et al. (2019) used fuzzy VIKOR for the green supplier selection problem. Opricovic (2004) compares VIKOR and TOPSIS based on evaluation metrics and a normalization method. While VIKOR performs based on minimum regret and maximum utility, TOPSIS performs based on the distance to ideal solution. On the other hand, VIKOR uses a linear normalization whereas TOPSIS adopts a vector normalization.

ELECTRE and PROMETHEE are other MCDM approaches for finding the best alternative for the supplier selection problem. They work based on the dominance of the alternatives on each other (Qu et al., 2020; Tong et al., 2022).

DEMATEL is another type of MCDM method that is based on determining the cause-effect relationship between the criteria. For example, Li et al. (2020) use this approach for the leagile supplier selection problem in Chinese Textile Industry. Giri et al. (2022) extend the idea by using a pythagorean fuzzy DEMATEL for the supplier evaluation in the case of sustainable supply chain management. As DEMATEL does not have ranking ability, it is integrated with other methods to rank the alternatives. For instance, Zhang et al. (2021) determine the causal relationship between the supplier selection criteria by DEMATEL and rank the suppliers by fuzzy VIKOR.

The use of integrated methods in MCDM

Integrated MCDM approaches have the advantages of overcoming the limitations of the individual methods. For instance, Ozcan et al. (2018) combine AHP and TOPSIS for the gas supplier selection while Mohammed et al. (2019a) integrate DEMATEL, ELECTRE and TOPSIS for the vendor selection problem. Recently, Çalık (2021) integrate AHP and TOPSIS for the green supplier selection problem in Industry 4.0 era and Mohammed (2020b) combine DEMATEL and VIKOR methods to develop the integrated "gresillient" supply chain management approach. Here, both green and resilience aspects of the supplier selection problem are considered. The author used DEMATEL to determine the relative importance of the decision criteria based on expert knowledge and VIKOR to rank the performances of the suppliers based on the gresillience criteria.

Incorporation of fuziness in MCDM

Due to uncertainty of decision making with expert knowledge, the integration of a fuzzy approach with MCDM methods is well received by the MCDM researcher community. Here, the idea is to transform linguistic expressions of experts such as low, medium and high into a trapezoidal or triangular type membership (Zhang et al., 2017; Liu et al., 2019; Darbari et al., 2019). Si et al. (2019) propose an effective ranking approach based on a fuzzy approach. Govindan et al. (2015) emphasize the fuzzy prevalence in the review of multi-criteria decision making approaches for a green supplier evaluation and selection. Recently, Liu et al. (2020) review the studies which use fuzzy AHP for dealing with subjective judgements. Jain et al. (2018) use fuzzy AHP and TOPSIS for the supplier selection problem in the automotive industry.

Awasthi et al. (2018) use integrated fuzzy AHP-VIKOR approach for the multi-tier global supplier selection problem. Çalık (2021) integrates fuzzy AHP and fuzzy TOPSIS for green supplier selection in industry 4.0 era. Venkatesh et al. (2019) adopt fuzzy AHP and fuzzy TOPSIS for partner selection in humanitarian logistics. Singh et al. (2018) integrates fuzzy AHP and fuzzy TOPSIS for the third party logistics partner selection for cold-chain. Ortiz-Barrios et al. (2020) integrated fuzzy AHP, fuzzy DEMATEL and TOPSIS for the selection of forklift filter suppliers. Fuzzy AHP is used for the determination of the weights of the criteria, fuzzy DEMATEL for the relations between the criteria and finally TOPSIS for ranking the alternative suppliers. On the other hand, Liu and Li (2019) use a different approach based on multi attribute decision making method that relies on generalized maclaurin symmetric mean aggregation operators for probabilistic linguistic information.

2.2 Brief literature review on BN

BNs are also effective tools for dealing with uncertainty due to probabilistic structure (Hosseini & Ivanov, 2019). As BNs are adopted in this study, a more informative way on how it is used is given in the next section. They provide reliable predictions based on the causal relationship between the items in the network (Topuz et al., 2018). This type of networks have shown to provide effective tools for decision making based on expert knowledge (Fenton et al., 2007). BNs have the advantage of being able to deal with uncertainty while considering the causal relationship between the decision criteria (Hosseini & Barker, 2016). Hosseini and Ivanov (2019) used BNs for the resilience measure of supply networks. There is an important research gap about this issue in the literature. BNs has the flexibility to work even if there is incomplete knowledge. This is usually achieved by estimating the missing knowledge based on the causal relationship between the criteria. This can be considered as a dynamic evaluation tool. In other words, when a decision maker has a new evidence about a given criterion, BNs update the entries of the network based on the entered evidence as posterior probabilities. This demonstrates that BNs are effective tools to evaluate alternatives based on the causal relationship between the selection criteria.

For instance, Sener et al. (2021) use Bayesian belief networks to examine the effect of information sharing, quality of shared information, commitment and information on supplier performance in aircraft manufacturing supply chain in US. Dohale et al. (2021) integrates Delphi-MCDM and BNs for production system selection problem. Hosseini and Barker (2016) evaluates alternative suppliers based on three main criteria; primary, green and resillience and in sub-criteria of these main criteria by BNs. In addition, BNs have the capability to work with incomplete knowledge. There is a research gap in the literature for these approaches in case of incomplete knowledge. In case there is missing information about any decision criterion, BNs estimates them based on the causal relationship between the criteria. However, the elicitation of the probabilities based on expert knowledge is a challenge for BNs. To respond to this critical issue, Yazdi and Kabir (2020) propose to integrate fuzzy evidence theory with BNs for process system risk analysis. Another practical tool for this challenge is Ranked Nodes tool of BNs. Ranked Nodes establish node probability tables of BNs based on the qualitative judgement of experts in ordinal scale as"low", "medium" and "high" (Fenton et al., 2007, Laitila & Virtanen, 2016). For example, Kaya and Yet (2019) used Ranked Nodes for building BN for the supplier selection problem and evaluated alternative suppliers based on each supplier evaluation criterion. Although Ranked Nodes is reliable and is a user friendly tool, there is a gap in the application of the Ranked Nodes in the literature.

Also, it is worth stressing that there is no systematic way of determining the causal structure of BNs. Kaya and Yet (2019) adopted DEMATEL to resolve this issue with DEMATEL being used to determine the cause-effect relationship between the criteria. Very recently, Li et al. (2020) also used DEMATEL for the supplier selection problem in a Chinese Textile Industry to determine the most influential criteria for the evaluation of suppliers based on the cause-effect relationship between the criteria. Kaya and Yet (2019) also determined the causal relationship between the criteria based on DEMATEL and then parameterized the BN with Ranked Nodes systematically. In this network, the buyer can evaluate alternative suppliers based on each criterion. However, it is worth noting that the network does not rank the alternatives based on the overall performance. In this study, we propose to extend the work of Kaya and Yet (2019) by producing a ranking of the suppliers. To achieve this, we incorporate TOPSIS into our methodology.

2.3 An overview of our integration approach

The integration of MCDM with Mathematical Programming and Artificial Intelligence (AI) methods has also shown recently to provide more effective methods in which the weakness of a given method is compensated by the others (Mohammed et al., 2021; Liu et al., 2019; Luan et al., 2019). In this study, we propose to integrate MCDM methods and BN as one of the AI approaches.

The strengths and limitations of the methods used in the proposed approach are summarised in Fig. 1.

Fig. 1

Strengths and limitations of the methods used in the proposed approach

In this study, we propose TOPSIS as a ranking approach and AHP for the elicitation of the weights of criteria for TOPSIS. This strategy is shown to be effective as recently demonstrated by Mohammed et al. (2021); Singh et al. (2018); Venkatesh et al. (2019) who also used AHP for the elicitation of weights of the criteria for the supplier selection problem. According to these recent studies, we can conclude that the integration of AHP and TOPSIS is useful for the purposes of obtaining the relative importance of the decision criteria and the evaluation of the alternatives respectively for multi criteria problems with expert knowledge. It was also noted that the elicitation of the weights of the criteria can also be determined by DEMATEL (Mohammed et al., 2019a; Mohammed, 2020b). It is also worth noting that DEMATEL aims to determine the weights based on the cause and effect relationships and prioritizes the cause attributes than the effect attributes contrarily to AHP which prioritizes the criteria based on the relative preferences of the experts. It is therefore appropriate to take advantages of the strengths of these two MCDM methods by using DEMATEL for building causal graph and AHP for the calculation of the weights of the criteria.

This integration would provide a systematic and a user friendly way to evaluate the alternatives. It helps the experts to submit their available knowledge with linguistic expressions and calculates the relative performances of the suppliers in a probabilistic way. One of the important contributions of this study is the ability of working with incomplete knowledge and making reliable probabilistic estimations.

There is therefore a gap in the literature for decision making with incomplete expert knowledge. We propose to use BN for this purpose and elicit the expert knowledge by Ranked Nodes tool. BN estimates the missing information probabilistically based on the causal relationship between the criteria and provide full initial decision matrix to TOPSIS. The results are updated with new information dynamically. In terms of dealing with uncertainty and using expert knowledge, BNs with Ranked Nodes tool is found to be a good alternative to fuzzy approach as it considers the causal relationship between the criteria, estimates the missing information and updates the network with new information dynamically. We also obtain the weights of criteria which is another input of TOPSIS using AHP. We build the causal graph of BN based on DEMATEL.

In summary, in this study we develop a novel, dynamic and systematic integrated approach for decision making with incomplete expert knowledge.

3 Main ingredients of the methodology

The proposed approach will be described in the next section. Here, we present some of the techniques that will be used. The following three MCDM approaches namely, the AHP, TOPSIS and DEMATEL will be incorporated into our methodology. As these are commonly known we do not include them here but more information is given in Appendix A for completeness. We also use Bayesian networks (BNs) with Ranked Nodes (RNs). As these are relatively less known, we first provide a brief description of BNs and how RNs are implemented.

3.1 Bayesian networks

Bayesian Networks are probabilistic graphical decision making tools (Fenton & Neil, 2013). They work based on Bayes’ Theorem and make inferences based on the prior beliefs of experts. They are able to make inferences even with partial evidence. When new evidence is obtained, BNs calculate the posterior probabilities and update all the network based on the new evidence. BNs are comprised of nodes and arcs which represent variables and causal relationship between variables respectively. Each node has its own Node Probability Table(NPT) which includes the conditional probability distribution parameters of that node (Kaya & Yet, 2019). BNs have the advantage in terms of representation of causal relationships between variables graphically. It analyses the causal relationship between variables probabilistically and systematically. BNs have also the flexibility in working with expert knowledge resulting in producing updated results based on the obtained new evidences.

3.2 Ranked nodes

Ranked Nodes (RNs) are expert friendly tools of BNs for decision making based on human judgement. RNs work based on doubly Truncated Normal (TNormal) distribution with scaled states [0–1] and approximate this distribution with a discrete BN node with equal width intervals (Fenton et al., 2007). RNs work with weighted functions such as the weighted mean (WMEAN), the weighted minimum (WMIN) and the weighted maximum (WMAX). These three measures are used to determine the central tendency of child node depending on the parent nodes.

An illustrative example is displayed in Figure 2 (Kaya & Yet, 2019). This shows a TNormal distribution with mean 0,7 and variance 0,1 on the left and ranked node approximation of this distribution on the right. This ranked node has 5 states, so it approximates the probability density under 5 equal width intervals (i.e., [0,0.2), [0.2,0.4), [0.4,0.6), [0.6,0.8) and [0.8,1]).

Fig. 2

Graph of an item with TNormal distribution(left) and with ranked nodes (right)

The main advantage of ranked nodes is that they require fewer number of parameters than their node probability tables (NPTs) counterparts. Besides, RNs are flexible enough to define a wide variety of shapes. An NPT has probability values of a node for each state combination of its parents. Therefore, the number of parameters in an NPT is the cartesian product of the number of its parents’ states and its states. For example, the BN model in Fig. 3 has three variables A, B, C where A is dependent on B and C, and each node has 5 states. Without using RNs, the number of probability values that need to be elicited from experts for the NPT of A is therefore $5^{3}=125$. This is not only time consuming task for the experts but can also be confusing resulting in misleading information.

Fig. 3

Example network

The construction of NPTs by ranked nodes consists of the following steps.

• Firstly, the states of a ranked node are determined.

• The type of the weighted function to be adopted is selected.

• The weights and variances of its parents are determined.

• NPTs are then calculated based on the TNormal approximation. This is performed automatically by the software AgenaRisk ( Fenton et al. (2007)).

For instance, if we use ranked nodes for our example model in Fig. 3, we need to define 3 parameters. These include the weights of Y and Z and the variance of X to define NPT of X as shown in Fig. 4.

Fig. 4

Parameters for NPT of X with ranked nodes

4 A novel integrated approach

We develop an integrated approach that combines DEMATEL, AHP, TOPSIS and BNs for the supplier selection problem. We first provide an overview of the algorithm, followed by the algorithm itself and some explanation of the main steps.

4.1 An overview

We adopt an approach that consists of four stages,

• 1. Use DEMATEL to determine the causal graph of BN,

• 2. Apply AHP to find the weights of the criteria,

• 3. Implement BNs to provide the evaluation matrix of alternatives for TOPSIS,

• 4. Use TOPSIS to rank the alternatives.

A basic flow chart is given in Fig. 5 and the main steps of the algorithm which we refer to as "MCDM-BN" are summarized in Fig. 6. It is worth noting that this approach can easily be made applicable for other multi-criteria type problems.

Fig. 5

Flow chart of the MCDM and BN integrated approach (MCDM-BN)

4.2 The MCDM-BN algorithm

Figure 6 describes the summary of the MCDM-BN algorithm.

Fig. 6

The integrated MCDM-BN algorithm

In Step 1, experts determine the main criteria for the supplier selection decision.

In Step 2, the relative importance of the decision criteria are found using the pairwise comparison of criteria of AHP. There are obviously several other available methods for determining the weights of the criteria. These include for instance the entropy method, SWARA and Simos method (Kobryn, 2017). DEMATEL can also be applied as a weighting method (Baykasoglu et al., 2013). As we already use DEMATEL in our proposed approach for the construction of BNs, we also elicit the weights of the criteria based on DEMATEL and evaluate the results with the experts in the case study. In the last step of DEMATEL, the total relation matrix(T) is obtained. This matrix has two important indicators, namely, the importance indicator($t^{+}$) and the relation indicator($t^{-}$) which are sums of and differences between the rows and columns of the total relation matrix, respectively. The weights of the criteria which are represented by $w_{i}$ are then calculated with the following formulas:

$$\begin{aligned} z_{i}= & {} {\left( {(t^{+})}^2+ {(t^{-})}^2\right) }^{1/2} \end{aligned}$$

(1)

$$\begin{aligned} w_{i}= & {} \frac{z_{i}}{\sum _{i=1}^{n} z_{i}} \end{aligned}$$

(2)

We conducted a DEMATEL survey with purchasing experts. The total relation matrix(T) is presented in Table 1 and the weights of the criteria which are calculated based on DEMATEL are given in Table 2.

Table 1 Total relation matrix

Table 2 Weights of the criteria by DEMATEL

Kobryn (2017) produced an interesting modification of the formulas of the calculation of the weights of the criteria using DEMATEL. These are defined in the following equations:

$$\begin{aligned} \bar{t_{i}}= & {} \frac{1}{2} \left( t^{+} + t^{-}\right) \end{aligned}$$

(3)

$$\begin{aligned} w_{i}= & {} \frac{\bar{t_{i}}}{\sum _{i=1}^{n}\bar{t_{i}}} \end{aligned}$$

(4)

The corresponding results related to the modified DEMATEL rule as defined by Kobryn (2017) are presented in Table 3.

Table 3 Weights of the criteria by DEMATEL using the modified rule

We also calculated the weights of the criteria based on the AHP in Step 2 of the case study. The results are given in Table 4.

We evaluated the results of these two strategies with the experts. They state that the weights elicited by AHP represent better their preferences. DEMATEL is used to determine the cause-effect relationships and gives more importance to the criteria which have cause-effect on the other criteria. Based on the above information, we therefore opted to use AHP for the elicitation of the weights of the criteria.

the alternatives based on the causal relationship between the criteria. When any evidence is entered to any criterion, BNs update the rest of the network based on the causal relationship between the criteria which are determined by DEMATEL. However, it is worth noting that the initial causal graph which was obtained by DEMATEL may not be a convenient causal network for BNs as it may include cycles. After the construction of the initial causal graph, cycles are eliminated using the interesting rules constructed by Kaya and Yet (2019).

In Step 4, the causal graph of BN is built based on the causal graph obtained from DEMATEL and the states of the nodes in BN are also determined.

In Step 5, we use Ranked Nodes to parameterize the BN. This is mainly because these are easy to elicit the expert knowledge from experts as a parameter of BN. The weighted function of Ranked Nodes, known as the WMEAN function, is used as the Ranked Node function. The central tendency and variance of child nodes are determined with the weights and variances of the parent nodes via the WMEAN function. The weights of the parent nodes are then elicited from the direct relation matrix of DEMATEL. On the other hand, the variance values are summed for each child node and normalized to the unit scale of TNormal Distribution. In this study, AgenaRisk software is used to compute the BN model automatically where Ranked Nodes are already inserted in the software.

In Step 6, the decision matrix is elicited from experts as it is one of the inputs of TOPSIS. In this matrix, alternatives are evaluated based on the selection criteria by the experts. Experts may not have a complete knowledge about all attributes of the suppliers. In this case, they submit their available knowledge about the alternatives.

In Step 7, in case there are missing values in the decision matrix for TOPSIS, BNs estimate these elements to complete the decision matrix.

In Step 8, TOPSIS uses the weights of the criteria and the decision matrix as an input and proceed with the matrix calculations to compute the geometric distance to the best and the worst alternatives. The alternatives are then ranked based on the smallest distance to the best alternative and the largest distance to the worst alternative.

5 Case study

To illustrate the approach, we use the following example based on a case study carried out with a forging company in Turkey. This company outsources machining operation and they have alternative suppliers for this operation. In this case study, we evaluated the eight alternative suppliers used by the company with three purchasing experts from the company.

The experts are chosen to reflect a wider view of the suppliers and their long term relationship with the company. We discussed about the surveys with the company’s planning and stock control manager. She assigned two purchasing experts and a planning and stock control supervisor as the experts for the survey. A survey that incorporates both quantitative and qualitative aspects was then constructed and given to these experts. We conducted AHP with planning and stock control supervisor of the company. We asked her to compare the criteria and suppliers based on the criteria pairwise manner. The other experts did not involve the survey of AHP as the pairwise comparison of eight alternative for 5 criteria takes a long time. However, for the DEMATEL survey all three experts were involved. They scored the effects of the criteria on each other. We processed the DEMATEL based on the average evaluation scores of the experts. A general discussion and explanation were also provided as part of this data gathering exercise.

For simplicity, we refer to these suppliers as Supplier A,..., Supplier H. Some explanation of the steps of the approach as given in Fig. 6 are provided below.

• 1. Identify decision criteria. Experts determined the decision criteria as product quality, delivery performance, price, cooperation and reputation based on the supplier selection criteria given in Kaya and Yet (2019).

• 2. Determine the weights of criteria. In this case study, the weights of the criteria in step 2 were initially calculated by both DEMATEL and AHP for a better understanding. However, the discussion with the purchasing experts in the company led to a conclusion that the AHP-based results represent their preferences much more than those derived by DEMATEL. AHP was therefore conducted to determine the weights of the criteria. The pairwise preferences of the experts among the decision criteria asked in a scale of 1–3–5–7–9 then averaged out the values and rounded to adhere the scale. The pairwise comparison matrix of criteria is presented in Table 4.

Table 4 Pairwise comparison matrix of the criteria

After processing the matrix computations, the weights of the criteria are obtained and presented in Table 5.

Table 5 Weights of the criteria

A consistency check is then conducted and the consistency index(CI) is found as 0.028. As $CI<0.1$, the judgements are considered as consistent.

• 3. Determine the causal relationship between the decision criteria. Causal relationships between criteria are determined by DEMATEL. We conducted DEMATEL survey in a 0-3 scale with three purchasing experts from the company and aggregated their values by basically having the average of their responses. The direct relation matrix of the DEMATEL is presented in Table 6.

Table 6 Direct relation matrix

The threshold value is set to 2 by the experts in this case study. The values above 2 are considered accepted as direct causal relation between the corresponding criteria. According to Table 6, there is a direct causal relation between product quality and price, delivery performance and price, product quality and delivery performance, cooperation and delivery performance, product quality and reputation, and finally delivery performance and reputation. The causal graph of the criteria is presented in Fig. 7.

• 4. Construct BN and define its states. As mentioned earlier we use Ranked Nodes. The states of the nodes are therefore determined in an ordinal scale, namely, very high, high, medium, low and very low.

• 5. Parameterize the BN with Ranked Nodes. We propose to use Ranked Nodes to parameterize the BN with WMEAN as the Ranked Node function as we also noted earlier. Weights of the parent nodes were elicited from the direct relation matrix of DEMATEL. For example, according to causal relationship between the criteria, the parents of price are product quality and delivery performance where the weights of product quality and delivery performance for mean of price node are 2.67 and 2.67. On the other hand, the variance values are summed for each child node and normalized to the unit scale of the TNormal Distribution[0-1]. The variances of the values in the matrix are presented in Table 7.

Fig. 7

Causal graph

Table 7 Variances of criteria

The software AgenaRisk (Fenton et al., 2007) is used to automatically compute the BN model. As an example, see a snapshot in Fig. 8.

• 6. Elicit the decision matrix from the experts. Decision makers submitted their knowledge about the alternatives for each criterion on the five point ordinal scale as very high, high, medium, low and very low. This information is presented in Table 8. We then randomly deleted some of the knowledge to make BN estimate the missing knowledge. The evaluation of the alternatives with missing knowledge is given in Table 9. We finally entered the knowledge of the experts as evidence into the BN as shown in Fig. 9.

Fig. 8

Ranked nodes

Table 8 Evaluation of suppliers based on criteria

Table 9 Evaluation of experts with missing knowledge denoted by ‘–’

Fig. 9

Example BN with ranked nodes for supplier E

• 7. Estimate the missing values in the decision matrix. BNs submit their knowledge about the alternative suppliers as provided in Table 9.

If there is missing knowledge, BN estimates the missing values. In this case study, to validate this process we purposely deleted some of these knowledge values randomly and make BN estimate these missing values. For example, for supplier E, the experts submitted that the delivery performance is medium, the price is high, the cooperation is high and the reputation is medium. The knowledge of the experts about product quality of supplier E is deleted and expected the BN to estimate it based on causal relations between the criteria. The available knowledge are entered as evidence. The elicitation of probability of product quality for supplier E with BN by AgenaRisk software is presented in Fig. 10. According to the estimation of BN, the product quality of the supplier E is estimated as 0.61 which is slightly above medium. We can perform similar operations for all suppliers and assess the performance of each supplier based on each criterion with this illustrative network.

Fig. 10

Estimation of probability of product quality for supplier E

Expert knowledge about all the criteria for all suppliers is entered as evidence to the network with linguistic expressions by Ranked Nodes. The BN turns these knowledge into probabilistic estimations with the considerations of causal relations between the criteria. The full estimation of BN with incomplete knowledge is presented in Table 10.

Table 10 Probabilities of criteria elicited from BN

• 8. Rank alternatives with TOPSIS. The weights of the criteria are obtained by AHP and the decision matrix is given by BN as inputs for TOPSIS which finally ranks the alternative suppliers. The results are given in Table 11.

Table 11 Ranking of suppliers

According to the results, supplier A is ranked as the best supplier, both supplier B and supplier C, and also both supplier D and supplier G have the same performance values. This case study illustrates that we can evaluate the suppliers based on each evaluation criterion by BN even when the experts do not have knowledge about some criteria and rank the suppliers based on their overall performance by TOPSIS.

6 Scenario analysis for knowledge value

To assess the effects of the knowledge value and robustness of the proposed approach, a sensitivity analysis is conducted by using various scenarios with different levels of missing values.

6.1 Performance measures

We assess the robustness of the approach using the following two evaluation measures:

a) Total number of mismatch ($T_{m}$)

Let n refer to the number of suppliers,

$\tilde{P_{i}}$ refers to the original or default position of the $i^{th}$ supplier(i.e., no missing value); $i=1,\dots ,n$

$P_{i}$ the position of the $i^{th}$ supplier in the new list when there are some missing values; $i=1,\dots ,n$

$$\begin{aligned} T_{m}=\sum _{i=1}^{n} m_{i} \end{aligned}$$

$$\begin{aligned} where \quad m_{i} ={\left\{ \begin{array}{ll} 1, &{} \hbox { if}\ P_{i}\ne {\tilde{P_{i}}} \quad i = 1,\dots ,n\\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

b)Total distance of mismatch $D_{m}$

This refers to the sum of mismatch for each supplier which is defined as

$$\begin{aligned} D_{m}=\sum _{i=1}^{n}{d(P_{i},{\tilde{P_{i}}})}=\sum _{i=1}^{n}{\mid P_{i}-{\tilde{P_{i}}} \mid } \end{aligned}$$

with $\mid P_{i}-{\tilde{P_{i}}} \mid$ is the distance between $P_{i}$ and $\tilde{P_{i}};\ i= 1,\ldots ,n$.

Illustrative Example

We presented an illustrative example for sensitivity analysis for knowledge value and robustness of the proposed approach. We compared the case of missing knowledge against complete knowledge. We already obtained the list with missing knowledge in the case study section which is presented in Table 11. We also ranked the same alternatives with complete knowledge of the experts and obtained the list in Table 12.

Table 12 Ranking of suppliers with complete knowledge

When we compare the list with complete knowledge and the list with missing knowledge, 3 mismatch items are generated which include Supplier E, Supplier G, Supplier D. Their total position distance of mismatch items is 4 as E mismatched by 2, G by 1 and D by 1.

6.2 Statistical analysis

We replicated the approach 10 times for these 8 suppliers and 5 criteria while varying the number of missing value from 5% to 20% with an increment of 5. Figure 11 shows the total number of mismatch whereas Fig. 12 displays the total position distance of mismatch as the number of missing value increases. According to both graphs, as one may expect, the total distance and the number of mismatch increase with the number of missing values. The marginal change appears to be relatively higher when the % of missing values($m_{i}$) is low (ie 5%, 10%) and they slowly stabilise. In other words, we have for $m_{i}=5\%$, $T_{m} =2.4$ & $D_{m}=3.2$, these values increase for $m_{i}=10\%$ to 3.6 and 4.8 then their relative increase slow down afterward. These results indicates the value of knowledge. By the increase of the available knowledge, more reliable estimations can be obtained.

Fig. 11

Effect of mismatch on % of missing values

Fig. 12

Effect of average position on % of missing values

Although we can observe the value of available knowledge when the % of missing values($m_{i}$) is low (ie 5%, 10%), the change stabilizes afterward and hence we can conclude, though the analysis is limited to this illustrative example, that the proposed approach can be robust for the different levels of missing values.

7 Conclusion, limitations and suggestions

Conclusions

In this study we develop a robust and effective approach which integrates MCDM and BNs. The proposed approach is able to work with incomplete expert knowledge and makes reliable probabilistic estimations. It is a dynamic approach which updates performance of the alternatives among all the decision criteria according to any obtained new information about the criteria and causal relationship between them. The Ranked Nodes tool offers an alternative friendly way of submitting qualitative knowledge of experts and turns them into probabilistic numbers in a well presented and easy to read causal network.

We discussed the estimation performance of BN for the missing part of the network with the purchasing experts of the company in our case study. They found the results reliable. However, for a more robust performance evaluation, more data can be collected about the suppliers and their real performance and the estimations based on each criterion can then be compared.

Our approach uses TOPSIS to rank the alternative suppliers with the weights of the selection criteria for TOPSIS obtained by AHP. The initial evaluation matrix for TOPSIS is estimated by BN. DEMATEL is used for determining the causal graphical structure of the BN. We developed two performance criteria of mismatch, namely, the distance as well as the number of mismatches. A sensitivity analysis using several levels of missing values, ranging from 5% to 20% with an increment of 5%, is conducted. Interesting results show that our approach is robust as the degree of mismatch does not deteriorate significantly with the increase in the number of missing values.

Limitations

The current study is limited to one case study only as the research arose from this particular industrial project. One way forward would be to identify a number of case studies that have different levels of missed information to assess whether the approach we developed will remain robust. On the other hand, there are different ways of elicitation of the weights of the decision criteria by DEMATEL, we only used one of the versions, other ones can be applied which could result in a richer discussion with the experts. It is also worth stressing that there are other approaches for obtaining the weights of the criteria which can then be integrated as well into the approach. In the case study, for our data gathering we relied on three experts from the company only. All of them involved the survey for DEMATEL but only one expert for the survey of AHP. The obtained results may not be very robust though the outcome in this occasion was satisfactory. To be consistent and more reliable one way would be to extend the data gathering by inviting similar type of experts from other similar companies. A larger data set would obviously lead to more informative and robust conclusions. In this paper, we conducted a case study for the supplier selection problem. However, our proposed approach can be applicable for other industry problems, particularly in case of incomplete knowledge, it will provide reliable decision making based on probabilistic estimations of the missing knowledge.

Suggestions

In this work, we used TOPSIS as a ranking method but other MCDM ranking methods such VIKOR, ELECTRE or PROMETHEE can also be adopted. Our approach could also be extended to incorporate invaluable information derived from commonly used statistical techniques on missing values. One way of tackling the aspect of uncertainty and vagueness could be to incorporate rough set theory as successfully implemented in some models in forecasting by Sharma et al. (2020). Another interesting though challenging avenue would be to incorporate fuzzy information in some of these techniques by considering a mixture of memberships to better represent each of the criteria from a fuzzy environment view point. A very recent and informative review chapter on MCDM with fuziness is given by Zeshui and Zhang (2022) and could be used as a basis for exploring several aspects in that particular but challenging area of research.

Appendix

1.1 A1: Analytical hierarchy process (AHP)

Analytical Hierarchy Process (AHP) is a well-known MCDM method. It works based on the pairwise comparison of criteria and alternatives. The relative importance of criteria and then relative preferences between alternatives for each criterion are provided by decision makers. Decision makers submit their preferences in AHP pairwise comparison scale (Saaty 1980) which is presented in Table 13.

Table 13 AHP pairwise comparison scale

The pairwise comparison matrix in AHP is a reciprocal matrix with its diagonal elements are 1, and the lower triangular of the matrix is reciprocal of the upper triangular matrix. An example pairwise comparison matrix is presented in Table 14.

Table 14 Example pairwise comparison matrix

Fig. 13

Notations of steps of AHP

Fig. 14

Steps of AHP

The pairwise comparison matrix of criteria is used to compute the priorities(weights) of criteria. In other words, the pairwise comparison of alternatives for each criterion is used to compute the priorities(preferences) of alternatives for each criterion. In the last step of the method, the priority vector of each alternative is multiplied by the corresponding priority value(weight) of the criterion and the alternatives are then ranked based on the overall priority values. Since AHP works based on the subjective judgement of the decision makers, a consistency check is performed to assess if the judgements of decision makers are consistent. If a decision maker submits that alternative A is more preferable than alternative B(pairwise comparison matrix value of A vs B:3) and alternative B is more preferable than alternative C(B vs C:5), then the decision maker can not state that alternative is more preferrable than alternative A(C vs A:5). The consistency check is performed by computing the consistency index(CI). If the value of CI is below 0.10, the judgements are accepted as consistent. The main notations used in the AHP process are given in Fig. 13 and the main steps of the method are summarized in Fig. 14.

Table 15 Random consistency index (RI)

Random consistency index(RI) is determined based on the number of items being compared and table of RI is shown in Table 15.

1.2 A2: Technique for order preference by similarity to ideal solution (TOPSIS)

TOPSIS differs from AHP as it is a distance based MCDM method. It ranks the alternatives based on the distance from the ideal-solution and negative-ideal solution. In other words, the closer to the ideal, the better. The notation of TOPSIS are given in Fig. 15. The main steps of TOPSIS is explained in Fig. 16.

Fig. 15

Notatios of TOPSIS

Fig. 16

Steps of TOPSIS

1.2.1 DEMATEL

DEMATEL determines the causal relationship between the criteria and strengths of the relationships. Chang et al. (2011) DEMATEL has two important matrices; direct relation matrix and total relation matrix. Direct relation matrix shows the direct influences between the criteria. Total relation matrix shows the total direct and indirect influences between the criteria. Total influence values above the threshold value is accepted as cause-effect relation between the related criteria. Steps of the DEMATEL are presented in the below:

• 1. The direct relation matrix A is constructed by asking the influence of decision criteria on each other on a 0 to 4 scale. If there are multiple experts and the average of their response for each influence is recorded in the direct relation matrix.

• 2. A normalized direct relation matrix M is obtained by dividing values of the direct relation matrix A with the maximum of sum of rows and columns:

  $$\begin{aligned} M= A* \min \left( \frac{1}{\max \sum _{i}^{n} a_{ij}} ,\frac{1}{\max \sum _{j}^{n} a_{ij}}\right) \end{aligned}$$

  (21)

  where $a_{ij}$ is the average direct relation matrix value for row i and column j.

• 3. The total relation matrix T represents the sum of direct and indirect relations:

  $$\begin{aligned} T = M+M^2+M^3+M^4+\dots \end{aligned}$$

  (22)

  It is calculated as follows:

  $$\begin{aligned} T = M\left( I-M\right) ^{-1} \end{aligned}$$

  (23)

  where I is the identity matrix.

• 4. For each criterion, the sum of the associated row R and column C is calculated. The criterion is classified as a net cause (sender) if R - C is positive, and it is classified as a net effect (receiver) if it is negative. The total relation strength of a criterion is represented by R + C.

• 5. A threshold value is defined by the domain experts and causal network is built by including the causal influences that are above the threshold in the total relation matrix. 17 shows an example causal graph built by DEMATEL. The vertical and horizontal axes in this figure represents the R-C and R+C values respectively. The arcs between variables represent whether the sum of direct and indirect strength of causal relations were above the threshold in the total relation matrix T. For example, the arc A to E represents that the presence of causal relation between A and E which is the sum of direct and indirect causal relations. This causal representation is quite different than BNs. In a BN, the arc A to E would represent a direct causal relation between A and E, and the indirect relations would be modelled by paths of directed arcs. As a result, DEMATEL results cannot be directly used for building BNs; they need to be systematically transformed. We present a novel method for this task in Sect. 5, and in the following section we present the supplier selection case study which we will use to illustrate our method.

Fig. 17

Example DEMATEL graph