Heterogeneity-adjusted management of pension funds using adaptive representative agents

Abstract

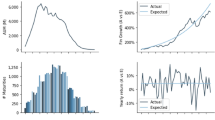
This paper focuses on defined-benefit pension funds in which heterogeneous plan members differ in age, salary, contribution rate, and other characteristics. The co-variation of these characteristics proves to have an important effect on the management of the fund. For example, we find that members’ ages and salary growths, if co-vary in unfavourable way, can substantially increase the funds’ liability, which in turn drives up the amount of funding required and the proportion of risky investment. This coupling effect of heterogeneity is demonstrated first through analytical statements which we derive under a simplified assumption of no investment constraints. In constrained cases for which analytical solutions are unavailable, we develop a numerical method that finds the heterogeneity-adjusted management decisions using a so-called adaptive representative agent (ARA), whose characterization is given explicitly in a key theorem. Whereas traditional methods often suffer from numerical complexity that grows exponentially with the number of heterogeneous members, the computational cost of the proposed ARA method is only linear in the number of time steps. This advantage of the ARA method and its ability to rectify the coupling effects of heterogeneity are demonstrated through our numerical example.

Appendices

Appendix I: Proof of Proposition 3.1

Before proving Proposition 3.1, let us first rewrite (3.1–3.2) by substituting the ${A}_{i,t}$ and ${B}_{i,t}$ from (3.3–3.4) to yield:

$${p}_{t}^{*} = \frac{\xi /\sigma }{{u}_{t}+{\xi }^{2}} \left[ \frac{{\mathcal{M}}_{t}+{u}_{t}{\mathcal{S}}_{t}/\xi -{Q}_{t}}{{W}_{t}} - 1 - r \right] ,$$

(A.1)

$${X}_{t}^{*} = \frac{{u}_{t}-1 }{{u}_{t}+{\xi }^{2}} \left[ {\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} - {Q}_{t} - \left(1+r\right){W}_{t} \right] ,$$

(A.2)

where ${\mathcal{M}}_{t}\,{:}{=}\,\frac{1}{1+r}{\sum }_{i=1}^{N}{B}_{i,t+1}{K}_{i}{\left(1+{\mu }_{i}\right)}^{{\tau }_{i}-t}{S}_{i,t}$, ${\mathcal{S}}_{t}\,{:}{=}\,\frac{1}{1+r}{\sum }_{i=1}^{N}{B}_{i,t+1}{K}_{i} (1+{\mu }_{i})^{{\tau }_{i}-t-1} \beta_{i} S_{i,t}$, and ${Q}_{t}={\sum }_{i=1}^{N}{\pi }_{i,t}^{^{\prime}}{S}_{i,t}$ (see (2.2)). Recall the definition that ${u}_{t}=1$ if no one retires at time $t$, and ${u}_{t}=1+{x}_{t}$ otherwise. In order to verify (A.1–A.2), the key is to show that the value function ${V}_{t}\left({W}_{t},{\mathbf{S}}_{t}\right)$ defined in (2.9) has the following form for all $t$:

$$ \begin{aligned} \frac{{V_{t} }}{{x_{t - 1} }} & = W_{t}^{2} - \frac{2}{1 + r}\left( {{\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} - Q_{t} } \right)W_{t} + {\Psi }_{t} \\ & = W_{t}^{2} - \frac{2}{1 + r}\mathop \sum \limits_{i = 1}^{N} B_{i,t} K_{i} \left( {1 + \mu_{i} } \right)^{{\tau_{i} - t}} S_{i,t } W_{t} + {\Psi }_{t} \\ \end{aligned} $$

(A.3)

where ${\Psi }_{\mathrm{t}}\,{:}{=}\,{\sum }_{i=1}^{N}{\sum }_{j=1}^{N}{v}_{ij,t}{S}_{i,t}{S}_{j,t}$ is a quadratic form in ${S}_{i,t}$’s with some fixed coefficients ${v}_{ij,t}$, independent of ${W}_{t}$. (The second equality in (A.3) follows directly from (3.3) and the definition of ${\mathcal{M}}_{t}$, ${\mathcal{S}}_{t}$, and ${Q}_{t}$.)

Let us prove (A.3) by induction on $t$. We begin by substituting ${R}_{t}$ from (2.3) into (2.5), to obtain ${W}_{t+1}=\left(\xi +{Z}_{t}\right){\Omega }_{t}+{\Upsilon }_{t}+{X}_{t}$, where

$${\Omega }_{\mathrm{t}}\,{:}{=}\,{\sigma }{p}_{t}{W}_{t}, \,{\text{and}}\, {\Upsilon }_{\mathrm{t}}\,{:}{=}\,\left(1+r\right){W}_{t}+{Q}_{t }.$$

Let ${\Gamma }_{\mathrm{t}}\,{:}{=}\,{\left[ {\Omega }_{\mathrm{t}} \left({\Upsilon }_{\mathrm{t}}+{X}_{t}\right)/{x}_{t }\right]}$. Then, (2.5) can be further simplified as${W}_{t+1}={\Gamma }_{t }{\left[ \xi +{Z}_{t} {x}_{t }\right]}^{T}$. Combined with ${S}_{i,t+1}={S}_{i,t}\left(1+{\mu }_{i}+{\alpha }_{i}{Y}_{i,t}+{\beta }_{i}{Z}_{t}\right)$ and the assumption that ${Y}_{i,t}$ and ${Z}_{t}$ are independent $\mathcal{N}\left(\mathrm{0,1}\right)$’s, we can write

$${E}_{t}\left[{W}_{t+1}^{2}\right] = {\Gamma }_{t}\left[ \begin{array}{cc}1+{\xi }^{2}& \xi {x}_{t}\\ \xi {x}_{t}& {x}_{t}^{2}\end{array}\right]{\Gamma }_{t}^{T} \text{and } {E}_{t}\left[{S}_{i,t+1}{W}_{t+1}\right] = {S}_{i,t}{\Gamma }_{t}\left[ \begin{array}{c}{\beta }_{i}+\xi \left(1+{\mu }_{i}\right)\\ {x}_{t}\left(1+{\mu }_{i}\right)\end{array} \right].$$

Therefore, assuming that (A.3) holds at time $t+1$, we can write ${E}_{t}\left[{V}_{t+1}/{x}_{t}\right]$ as

$${E}_{t}\left[\frac{{V}_{t+1}}{{x}_{t}}\right] = {\Gamma }_{t}\left[\begin{array}{cc}1+{\xi }^{2}& \xi {x}_{t}\\ \xi {x}_{t}& {x}_{t}^{2}\end{array}\right]{\Gamma }_{t}^{T} - 2{\Gamma }_{t}\left[\begin{array}{c}{\mathcal{S}}_{t}+\xi {\mathcal{M}}_{t}\\ {x}_{t}{\mathcal{M}}_{t}\end{array}\right] + {E}_{t}\left[{\Psi }_{t+1}\right] .$$

(A.4)

Note that, since ${\Psi }_{t+1}$ is quadratic in ${S}_{i,t+1}$’s and ${E}_{t}\left[{S}_{i,t+1}{S}_{j,t+1}\right] = {S}_{i,t}{S}_{j,t}\left(1+{\mu }_{i}+{\mu }_{j}+{\mu }_{i}{\mu }_{j}+{\beta }_{i}^{2}+{\alpha }_{i}^{2}{1}_{\left\{i=j\right\}}\right)$, the last term $E\left[{\Psi }_{t+1}\right]$ is quadratic in ${S}_{i,t}$’s.

Case 1: No retirement at time ${\varvec{t}}$ In this case ${X}_{t}=0$, ${\Gamma }_{\mathrm{t}}={\left[ {\Omega }_{\mathrm{t}} {\Upsilon }_{\mathrm{t}}/{x}_{t }\right]}$ and equation (A.4) simplifies to:

$$E\left[\frac{{V}_{t+1}}{{x}_{t}}\right]=\left(1+{\xi }^{2}\right){\Omega }_{t}^{2}-2\xi \left({\mathcal{M}}_{t}+{\mathcal{S}}_{t}/\xi -{\Upsilon }_{t}\right){\Omega }_{t}+{\Upsilon }_{t}^{2}-2{\Upsilon }_{t}{\mathcal{M}}_{t}+{E}_{t}\left[{\Psi }_{t+1}\right] .$$

(A.5)

The solution ${\Omega }_{t}^{*}$ that minimizes the above expression (which is simply quadratic in ${\Omega }_{t}$) can be easily found as

$${\Omega }_{t}^{*} = \frac{\xi \left({\mathcal{M}}_{t}+{\mathcal{S}}_{t}/\xi -{\Upsilon }_{t}\right)}{1+{\xi }^{2}}.$$

Since ${\Omega }_{\mathrm{t}}^{*}={\sigma }{p}_{t}^{*}{W}_{t}$ and ${\Upsilon }_{\mathrm{t}}=\left(1+r\right){W}_{t}+{Q}_{t}$, the above equation gives ${p}_{t}^{*}$ that confirms (A.1). Moreover, according to (2.9), the value function ${V}_{t}$ at time $t$ is obtained by substituting the minimizer ${\Omega }_{\mathrm{t}}^{*}$ into (A.5):

$$ \begin{aligned} \frac{{V_{t} }}{{x_{t} }} & = \frac{1}{{\left( {1 + r} \right)^{2} }}\left[ { - \frac{{\xi^{2} \left( {{\mathcal{M}}_{t} + {\mathcal{S}}_{t} /\xi - {\Upsilon }_{t} } \right)^{2} }}{{1 + \xi^{2} }} + \left( {{\mathcal{M}}_{t} - {\Upsilon }_{t} } \right)^{2} - {\mathcal{M}}_{t}^{2} + E_{t} \left[ {{\Psi }_{t + 1} } \right]} \right] \\ & = \frac{1}{{\left( {1 + r} \right)^{2} }}\left[ {\frac{{\left( {{\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} - {\Upsilon }_{t} } \right)^{2} + 2{\mathcal{S}}_{t}^{2} }}{{1 + \xi^{2} }} - {\mathcal{S}}_{t}^{2} - {\mathcal{M}}_{t}^{2} + E_{t} \left[ {{\Psi }_{t + 1} } \right]} \right] \\ \end{aligned} $$

(A.6)

Substituting ${x}_{t-1}={x}_{t}/\left(1+{\xi }^{2}\right)$ and ${\Upsilon }_{t}=\left(1+r\right){W}_{t}+{Q}_{t}$, and letting ${\Psi }_{t}={\left({\mathcal{M}}_{t}-\xi {\mathcal{S}}_{t}-{Q}_{t}\right)}^{2}+{\mathcal{S}}_{t}^{2}-{\mathcal{M}}_{t}^{2}-{\xi }^{2}\left({\mathcal{S}}_{t}^{2}+{\mathcal{M}}_{t}^{2}\right)+{x}_{t}E\left[{\Psi }_{t+1}\right]/{x}_{t-1}$, one can show that the display equation above is equivalent to (A.3).

Case 2: Some members retire at time $\,{\varvec{t}}$ Combining (A.4) with ${X}_{t}^{2}={\left({X}_{t}+{\Upsilon }_{t}\right)}^{2}+{\Upsilon }_{t}^{2}-2{\Upsilon }_{t}\left({X}_{t}+{\Upsilon }_{t}\right)$, we obtain

$$\frac{{X}_{t}^{2}+{E}_{t}\left[{V}_{t+1}\right]}{{x}_{t}} = {\Gamma }_{t}\left[\begin{array}{cc}1+{\xi }^{2}& \xi {x}_{t}\\ \xi {x}_{t}& {x}_{t}+{x}_{t}^{2}\end{array}\right]{\Gamma }_{t}^{T}-2{\Gamma }_{t}\left[ \begin{array}{c} \xi {\mathcal{M}}_{t}+{\mathcal{S}}_{t}\\ {x}_{t}{\mathcal{M}}_{t}+{\Upsilon }_{t}\end{array} \right] +\frac{{\Upsilon }_{t}^{2}}{{x}_{t}}+\frac{E\left[{\Psi }_{t+1}\right]}{{\left(1+r\right)}^{2}} .$$

(A.7)

The solution ${\Gamma }_{t}^{*}$ that minimizes the above expression (which is simply quadratic in ${\Gamma }_{t}$) can be easily found as

$$ \begin{aligned} {\Gamma }_{t}^{*} & = \left[ {\begin{array}{*{20}c} {1 + \xi^{2} } & {\xi x_{t} } \\ {\xi x_{t} } & {x_{t} + x_{t}^{2} } \\ \end{array} } \right]^{ - 1} \left[ { \begin{array}{*{20}c} { \xi {\mathcal{M}}_{t} + {\mathcal{S}}_{t} } \\ {x_{t} {\mathcal{M}}_{t} + {\Upsilon }_{t} } \\ \end{array} } \right] \\ & = \frac{1}{{u_{t} + \xi^{2} }}\left[ { \begin{array}{*{20}c} {\xi {\mathcal{M}}_{t} + u_{t} {\mathcal{S}}_{t} - \xi {\Upsilon }_{t} } \\ {{\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} + \left( {1 + \xi^{2} } \right){\Upsilon }_{t} /x_{t} } \\ \end{array} } \right] , \\ \end{aligned} $$

where ${u}_{t}=1+{x}_{t}$. With ${\Gamma }_{t}^{*}\,{:}{=}\,{\left[ \sigma {p}_{t}^{*}{W}_{t} \left({\Upsilon }_{\mathrm{t}}+{X}_{t}^{*}\right)/{x}_{t }\right]}$ and ${\Upsilon }_{\mathrm{t}}=\left(1+r\right){W}_{t}+{Q}_{t}$, one can show that the above equation gives ${p}_{t}^{*}$ and ${X}_{t}^{*}$ that confirm (A.1–A.2). And from (2.9), ${V}_{t}$ is obtained by substituting the minimizer ${\Gamma }_{\mathrm{t}}^{*}$ into (A.7):

$$ \begin{aligned} \frac{{V_{t} }}{{x_{t} }} & = \frac{1}{{\left( {1 + r} \right)^{2} }}\left[ { - \frac{1}{{u_{t} + \xi^{2} }}\left[ { \begin{array}{*{20}c} { \xi {\mathcal{M}}_{t} + {\mathcal{S}}_{t} } \\ {x_{t} {\mathcal{M}}_{t} + {\Upsilon }_{t} } \\ \end{array} } \right] \cdot \left[ { \begin{array}{*{20}c} {\xi {\mathcal{M}}_{t} + u_{t} {\mathcal{S}}_{t} - \xi {\Upsilon }_{t} } \\ {{\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} + \left( {1 + \xi^{2} } \right){\Upsilon }_{t} /x_{t} } \\ \end{array} } \right] + \frac{{{\Upsilon }_{t}^{2} }}{{x_{t} }} + \frac{{E\left[ {{\Psi }_{t + 1} } \right]}}{{\left( {1 + r} \right)^{2} }}} \right] \\ & = \frac{1}{{\left( {1 + r} \right)^{2} }}\left[ { \frac{{\left( {{\mathcal{M}}_{t} - \xi {\mathcal{S}}_{t} - {\Upsilon }_{t} } \right)^{2} }}{{u_{t} + \xi^{2} }} - {\mathcal{S}}_{t}^{2} - {\mathcal{M}}_{t}^{2} + \frac{{E\left[ {{\Psi }_{t + 1} } \right]}}{{\left( {1 + r} \right)^{2} }} } \right] . \\ \end{aligned} $$

Substituting ${x}_{t-1}={x}_{t}/\left(1+{\xi }^{2}\right)$ and ${\Upsilon }_{t}=\left(1+r\right){W}_{t}+{Q}_{t}$, and letting ${\Psi }_{t}={\left({\mathcal{M}}_{t}-\xi {\mathcal{S}}_{t}-{Q}_{t}\right)}^{2}-\left({u}_{t}+{\xi }^{2}\right)\left({\mathcal{S}}_{t}^{2}+{\mathcal{M}}_{t}^{2}\right)+{x}_{t}E\left[{\Psi }_{t+1}\right]/{x}_{t-1}$, one can show that the display equation above is equivalent to (A.3).

Thus, in both cases above, we have shown for an arbitrary $t$ that if (A.3) holds at time $t+1$, then it also holds at time $t$. Recall that ${V}_{{\tau }_{N}}$, by construction, satisfies the boundary condition:

$${V}_{{\tau }_{N}}={\left({K}_{N}{Y}_{N,{\tau }_{N}}-{W}_{{\tau }_{N}}\right)}^{2}$$

Thus, referring to the fact that ${B}_{N,{\tau }_{N}}=1+r$ and ${x}_{{\tau }_{N}-1}=1$ and letting ${\Psi }_{{\tau }_{N}}={\left(1+r\right)}^{2 }{K}_{N }^{2}{Y}_{N,{\tau }_{N }}^{2}$, one can see that (A.3) holds for $t={\tau }_{N}$. Hence, by induction, we (A.3) is verified for all $t\le {\tau }_{N}$, and so are the optimal decisions ${p}_{t}^{*}$ and ${X}_{t}^{*}$.

Appendix II: Proof of Proposition 4.1

Because of (4.4C) and (4.4G), multiplying both sides of (4.4H) by $1+{\mu }_{i}$ and then summing over $i=1$ to $N$ yields

$$1+{\mu }_{R} = \frac{\left(1+r\right){\mathcal{M}}_{t}}{{B}_{R,t+1 }{K}_{R }{\left(1+{\mu }_{R}\right)}^{{\tau }_{R}-t-1 }{S}_{R} } .$$

(A.8)

where ${\mathcal{M}}_{t}$ is as defined in Appendix I. And because of (4.4E), multiplying both sides of (4.4H) by ${\beta }_{i}$ and then summing over $i=1$ to $N$ yields

$${\beta }_{R} = \frac{\left(1+r\right){\mathcal{S}}_{t}}{{B}_{R,t+1 }{K}_{R }{\left(1+{\mu }_{R}\right)}^{{\tau }_{R}-t-1 }{S}_{R} } .$$

(A.9)

where ${\mathcal{S}}_{t}$ is as defined in Appendix I. If we substitute ${A}_{R,t}$ from (4.2) into (4.1) and use (A.8–A.9), we can rewrite ${\widehat{p}}_{R,t}$ in terms of ${\mathcal{M}}_{t}$ and ${\mathcal{S}}_{t}$ as:

$${\widehat{p}}_{R,t} = \frac{\xi /\sigma }{1+{\xi }^{2}} \left[ \frac{{\mathcal{M}}_{t}+{\mathcal{S}}_{t}/\xi -{\pi }_{R}{S}_{R}}{{W}_{t}} - 1 - r \right] .$$

(A.10)

Because (2.2) and (4.4B) imply that ${Q}_{t}={\pi }_{R}{S}_{R}$, one can readily see that ${\widehat{p}}_{R,t}$ in (A.10) matches exactly ${p}_{t}^{*}$ in (A.1). Hence, Proposition 4.1 is proved.