SpringerLink
Log in

Workload and short sickness absences in a cohort of Finnish hospital employees

  • OriginalPaper
  • Published:
The European Journal of Health Economics Aims and scope Submit manuscript

Abstract

This article used register data on day-to-day working hours of hospital employees combined with patient characteristics at work unit (wards) level to measure workload and its implications for short, self-certified sickness absences. We measured statistically the average nursing treatment burden of different patient mixes in hospital wards, and then analyzed the overall workload (intensity) of working days by comparing it to the actual available nursing workforce. We found that a significant part of the workload variation occurred between working days, and it was related to unexpected changes in the number of employees. In atypical situations a long work shift was associated with caring for patients with fewer resources. The high workload of a day increased the risk of short sickness absences along the following 3-week period. The results show that managing short-term workload variability should be a key aim from the perspective of well-being at work, and that combining different data sources can provide novel, important insights to the measurement of workload.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Source: the researchers’ own calculations. Notes: Point estimates and 95-% confidence intervals. The analysis was carried out with OLS estimation, where the variable to be explained was the person’s short sickness absence, and the explanatory variables were delayed workload estimates. The bootstrap** method was used in the evaluations to calculate confidence intervals. The data contains a total of slightly less than 200,000 person-level daily observations, depending on the resampling. The number of observations without previous (long) absences is ca. 43,000. All wards in the data were included, regardless of their size and the amount of data. Fixed person, month, day-of-the-week and year effects were also used as explanatory factors. The control variables also included all sickness absences and short sickness absences on the same day. The explanatory power R2 of the model is typically less than 0.05, depending on resampling

Fig. 4

Source: The researchers’ own calculations. Notes: The analysis was carried out with OLS estimation, where the variable to be explained was the person’s short sickness absence, and the explanatory variables were delayed workload estimates multiplied by the person’s corresponding number of working hours and the number of working hours alone. The bootstrap** method was used in the evaluations to calculate confidence intervals. The data contains a total of slightly fewer than 200,000 person-level daily observations. The number of observations without previous (long) absences is ca. 43,000. Fixed person, month, day-of-the-week and year effects were also used as explanatory factors. The control variables also included all sickness absences on the same day and short sickness absences in the ward. The explanatory power R2 of the model is typically less than 0.05, depending on resampling

Fig. 5

Source: The researchers’ own calculations. Notes: The analysis was carried out with OLS estimation, where the variable to be explained was the person’s short sickness absence, and the explanatory variables were delayed workload estimates multiplied by the person’s corresponding number of working hours and the number of working hours alone. The bootstrap** method was used in the evaluations to calculate confidence intervals. The data contains a total of slightly fewer than 200,000 person-level daily observations. The number of observations without previous (long) absences is ca. 43,000. Fixed person, month, day-of-the-week and year effects were also used as explanatory factors. The control variables also included all sickness absences on the same day and short sickness absences in the ward

Similar content being viewed by others

Data availability

The data is confidental and it is not publicly available.

Notes

  1. The main model we used classified the patient population into different burden categories by type of treatment, using the main categories of the Oulu patient classification (OPC). An average resource need was calculated separately for different patient categories, while treatments with no OPC classification were evaluated (only) according to their treatment type. In addition, the effect on the workload of the sub-categories of the OPC classifications was evaluated separately. The calculations were made separately for four different types of wards.

  2. The sources of the data have been described in more detail above. Titania data was used as the source of working hours, and patient data was compiled by combining ward-specific and anonymised OPC- and DRG-classified patient data.

  3. The guidelines are no longer available from public sources as they have been incorporated into a commercial service product.

  4. The day’s workload in relation to the average (estimated) burden is

    $${workload}_{i,t}=\frac{{\sum }_{l=1}^{n}{\beta }_{l}{patients}_{l,t}+{\epsilon }_{i}+{\epsilon }_{t}}{{Hours}_{i,t}}=1-\frac{{\epsilon }_{i,t}}{{Hours}_{i,t}}$$

    When the resource usage is average exactly as predicted by the model, \({\epsilon }_{i,t}=0,\) and the metric gets a value of 1.

  5. A broader discussion of the uncertainties is given in the “Discussion” section.

  6. Sampling is carried out with return, so that the same original observation can occur several times in a new sample.

  7. The coefficients of the linear probability model indicate how changing some characteristic of the conditions affects the probability of sickness absences in otherwise similar conditions. For example, if the coefficient associated with a previous workload k periods earlier is 0.01, an increase in the workload by 1 unit (by one average workload) would be 1 percentage point more likely to mean a sickness absence than in conditions with otherwise the same background factors.

    Adding cross-effect variables (in the “Appendix 1”) to the model makes it possible to investigate whether the increased level of the workload together with the cross-effect variable increases sickness absences (coefficient \({\alpha }_{k}^{r}>0\)) or decreases them (coefficient \({\alpha }_{k}^{r}<0\)).

  8. Temporary staff is not necessarily registered in Titania.

  9. In this case, wards with fewer than 1000 daily observations were also included in the data. Focusing on long observation periods dropped the number of observations from approximately 360,000 to just over 200,000, and the limited amount of data was no longer enough to make reliable observations.

  10. As an alternative, we also considered a two-step instrumental variable approach. The effect of workload to sickness absences was investigated by using variation in contemporaneous staffing level as a first-stage predictor of workload, and that prediction as an explanatory variable for the sick leaves in the second stage. In this case, our argument is that past difficulties in finding staff may identify (exogenous) variation in workload, and this variation can be used to make inferences on the impacts of workload on brief sickness absences. We find evidence of an initial large impact of similar size (0.005, p = 0.056) at the 1–3 day interval, while the usual first stage testing indicated that the instruments (average staffing levels with the same lag structure as the workload index variables) is appropriate.

  11. Recent work has been documented by Vähämäki et al. [75]. There are several administrative development projects in the background, which have been considered to provide new and valuable information about the resource variability and productivity of work tasks. The method has already been piloted in the social security system, HR services and tax administration as well as in fields such as maritime safety monitoring work.

  12. In practice, the subcategories are set as control variables in the evaluation of the groups divided into the main categories. Thus, the same patient is evaluated with several overlap** criteria. When information about the same treatment period is entered into the statistical model several times according to different classifications, the statistical model gives an estimate of the effect of a certain criterion on the patient’s burden while the other criteria are kept constant.

  13. If the patient’s main class remains the same, but the sub-categories in the OPC classification change, for example so that category 1 is A and 2 is C, the marginal change in the patient’s burden is $$({\beta }_{A,1}-{\beta }_{B,1})+({\beta }_{C,2}-{\beta }_{B,2})$$. The result shows that the changes in the OPC sub-classification are assumed to be the same in all treatment types while the general load of the treatment period type is controlled at the same time.

  14. In model 1, the different sub-categories are treated together through the overall classification.

  15. Together with the corresponding terms of classified patients, these terms are set in the (simplified) resource demand model presented above as factors explaining the working time (cf. $${\sum }_{l=1}^{n}{\beta }_{l}lk{m}_{l,i,t}$$ in the simplified model).

  16. In general, the assessments according to model 2 have a larger dispersion. The standard deviation of model 2 in the data shown in the graphs is 0.495, while it is only 0.358 in model 1.

References

  1. Heilmann, P.: To have and to hold: personnel shortage in a Finnish healthcare organization. Scand. J. Public Health 2010(38), 518–523 (2010)

    Article  Google Scholar 

  2. Pihlava, M.: Työkuormitus kasvoi julkisessa terveydenhuollossa. Lääkärilehti 19(1), 2023 (2023)

    Google Scholar 

  3. Simoens, S., Villeneuve, M., Hurst, J.: Tackling nurse shortages in OECD countries (2005)

  4. Turunen, V.: Avi: Meilahden leikkausosaston henkilöstö kovilla—työnantajan korjattava tilanne. Tehy-lehti. TEHY 13(11), 2018 (2018)

    Google Scholar 

  5. Marmot, M., Feeney, A., Shipley, M., North, F., Syme, S.L.: Sickness absence as a measure of health status and functioning: from the UK Whitehall II study. J. Epidemiol. Commun. Health 49(2), 124–130 (1995)

    Article  CAS  Google Scholar 

  6. Boschman, J.S., Noor, A., Sluiter, J.K., Hagberg, M.: The mediating role of recovery opportunities on future sickness absence from a gender- and age-sensitive perspective. PLoS ONE 12(7), e0179657 (2017)

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  7. Vedaa, Ø., Pallesen, S., Waage, S., Bjorvatn, B., Sivertsen, B., Erevik, E., Svensen, E., Harris, A.: Short rest between shift intervals increases the risk of sick leave: a prospective registry study. Occup. Environ. Med. 74(7), 496–501 (2017)

    Article  PubMed  Google Scholar 

  8. Janssen, N., Kant, I.J., Swaen, G.M., Janssen, P.P., Schroer, C.A.: Fatigue as a predictor of sickness absence: results from the Maastricht cohort study on fatigue at work. Occup. Environ. Med. 60(Suppl 1), i71-76 (2003)

    Article  PubMed  PubMed Central  Google Scholar 

  9. Suadicani, P., Olesen, K., Bonde, J.P., Gyntelberg, F.: Psychosocial work conditions associated with sickness absence among hospital employees. Occup. Med. (Lond.) 64(7), 503–508 (2014)

    Article  CAS  PubMed  Google Scholar 

  10. Ala-Mursula, L., Vahtera, J., Kivimäki, M., Kevin, M.V., Pentti, J.: Employee control over working times: associations with subjective health and sickness absences. J. Epidemiol. Commun. Health 56(4), 272–278 (2002)

    Article  Google Scholar 

  11. Delamaire, M., Lafortune, G.: Nurses in advanced roles. OCDE, ed. OECD Health Working Papers (54) (2010)

  12. Rainio, A.K., Ohinmaa, A.E.: Assessment of nursing management and utilization of nursing resources with the RAFAELA patient classification system—case study from the general wards of one central hospital. J. Clin. Nurs. 14(6), 674–684 (2005)

    Article  PubMed  Google Scholar 

  13. Fagerström, L., Rainio, A.K., Rauhala, A., Nojonen, K.: Validation of a new method for patient classification, the Oulu Patient Classification. J. Adv. Nurs. 31(2), 481–490 (2000). https://doi.org/10.1046/j.1365-2648.2000.01277.x

    Article  PubMed  Google Scholar 

  14. Kaustinen, T.: Oulu-Hoitoisuusluokitus Ja Hoitohenkilökunnan Ajankäyttö Hoitotyön Laatuvaatimusten Näkökulmasta. Acta Universitatis Ouluensis (2011)

  15. Luhtasela, L.: Hoitoisuuden vaikutus hoitotyöhön RAFAELA-järjestelmän avulla tarkasteltuna. Pro Gradu, Hoitotieteenlaitos, Lääketieteellinen tiedekunta, Tampereen Yliopisto (2006)

  16. Pusa, A.-K.: The right nurse in the right place: nursing productivity and utilisation for the RAGAELA patient classification system in nursing management. University of Kuopio, Dept. of Health Policy and Management (2007)

  17. Rauhala, A., Fagerstrom, L.: Determing the optimal nursing Intensift: the Rafaela method. J. Adv. Nurs. 45, 351–359 (2004)

    Article  PubMed  Google Scholar 

  18. Kaustinen, T.: Oulu-hoitoisuusluokitus ja hoitohenkilökunnan ajankäyttö hoitotyön laatuvaatimusten näkökulmasta (Oulu patient classification and use of working hours in nursing from the perspective of nursing care quality standards. In Finnish). Acta Universitatis Ouluensis, ISSN 0355-3221. Oulu, Oulun yliopisto. PhD: 177 (2011)

  19. Fagerström, L.: Professional assessment of optimal nursing care intensity level: a new method of assessing personnel resources for nursing care. J. Clin. Nurs. 8(4), 369–379 (1999)

    Article  PubMed  Google Scholar 

  20. Fagerström, L., Rauhala, A.: Benchmarking in nursing care by the RAFAELA patient classification system—a possibility for nurse managers. J. Nurs. Manag. 15(7), 683–692 (2007)

    Article  PubMed  Google Scholar 

  21. Liljamo, P., Kaakinen, P.: Cross-map** the Finnish classification of nursing diagnosis, nursing interventions and the Oulu Patient Classification. Stud Health Technol. Inform. 146, 774–775 (2009)

    PubMed  Google Scholar 

  22. Luhtasela, L.: Hoitoisuuden vaikutus hoitotyöhön RAFAELA-järjestelmän avulla tarkasteltuna, pp. 68–68 (2006)

  23. Pusa, A.-K.: The Right nurse in the right place: nursing productivity and utilisation of the RAFAELA patient classification system in nursing management, University of Kuopio, Dept. of Health Policy and Management, pp. 111–111 (2007)

  24. Rauhala, A., Fagerstrom, L.: Determining optimal nursing intensity: the RAFAELA method. J. Adv. Nurs. 45(4), 351–359 (2004)

    Article  PubMed  Google Scholar 

  25. Atkinson, L.: Atkinson review: measurement of government output and productivity for the national accounts. Final Report. Palgrave Macmillan (2005)

  26. Dunleavy, P., Carrera, L.: Growing the Productivity of Public Services. Edward Elgar Publishing, London (2013)

    Book  Google Scholar 

  27. OECD: OECD Compendium of Productivity Indicators 2015. OECD Publishing, Paris (2015). https://doi.org/10.1787/pdtvy-2015-en

    Book  Google Scholar 

  28. Diewert, W.E.: Productivity measurement in the public sector: theory and practice, microeconomics.ca working papers erwin_diewert-2017-1, Vancouver School of Economics, revised 02 Feb 2017 (2017)

  29. Simpson, H.: Productivity in public services. J. Econ. Surv. 23, 250–276 (2009). https://doi.org/10.1111/j.1467-6419.2008.00562.x

    Article  Google Scholar 

  30. Lau, E., Lonti, S., Schiltz, R.: Challenges in the measurement of public sector productivity in OECD countries. Int. Product. Monit. 32, 180–195 (2017)

    Google Scholar 

  31. The Finnish Audit Office: Tuottavuuden mittaaminen valtiolla. Valtiontalouden tarkastusviraston selvitys 4/2011 (2011)

  32. Evans, R.G., Schneider, D.G., Barer, M.L.: Health human resources productivity: what it is, how it’s measured, why (how you measure) it matters, and who’s thinking about it. Canadian Health Services Research Foundation (2010)

  33. Häkkinen, P.: Sairaaloiden tuottavuuden kehitys 2004–2008. Helsinki (2010)

  34. Koechlin, F., Lorenzoni, L., Schreyer, P.: Comparing price levels of hospital services across countries: results of pilot study. OECD Health Working Papers (53) (2010)

  35. Kotzian, P.: Productive efficiency and heterogeneity of health care systems: results of a measurement for OECD countries. Open Econ. J. 2(1), 20–30 (2009)

    Article  Google Scholar 

  36. Levitt, S.D.: Super freakonomics: global cooling, patriotic prostitutes, and why suicide bombers should buy life insurance. First Harper Perennial edition. New York: Harper Perennial (2011)

  37. Linna, M., Vesterinen, S., Juvonen, I.: Sairaaloiden tuottavuuden kehitys 2001–2005. 2355(09) (2007)

  38. Palfrey, S.: Daring to practice low-cost medicine in a high-tech Era. N. Engl. J. Med. 364(11), e21 (2011)

    Article  CAS  PubMed  Google Scholar 

  39. Tveiten, J.E., Flatum, C., Flato, G.D., Johannessen, K.-A., Aspholm Hole, S.: Makroanalyse av bemanning og produktivitet i somatisk En sammenligning av Norge, Danmark, Finland. Tyskland og Skottland, Oslo (2008)

    Google Scholar 

  40. Härmä, M., Ropponen, A., Hakola, T., Koskinen, A., Vanttola, P., Puttonen, S., Sallinen, M., Salo, P., Oksanen, T., Pentti, J., Vahtera, J., Kivimäki, M.: Develo** register-based measures for assessment of working time patterns for epidemiologic studies. Scand. J. Work Environ. Health 41(3), 268–279 (2015). https://doi.org/10.5271/sjweh.3492

    Article  PubMed  Google Scholar 

  41. Rosenstrom, T., Harma, M., Kivimaki, M., Ervasti, J., Virtanen, M., Hakola, T., Koskinen, A., Ropponen, A.: Patterns of working hour characteristics and risk of sickness absence among shift-working hospital employees: a data-mining cohort study. Scand. J. Work Environ. Health (2021). https://doi.org/10.5271/sjweh.3957

    Article  PubMed  PubMed Central  Google Scholar 

  42. Krutova, O., Ervasti, J., Virtanen, M., Peutere, L., Härmä, M., Ropponen, A.: Work unit level personnel working hours and the patients’ length of in-hospital stay—an administrative data approach. PLOS Digit Health 2(5), e0000265 (2023). https://doi.org/10.1371/journal.pdig.0000265

    Article  PubMed  PubMed Central  Google Scholar 

  43. Pirkanmaa: About the wellbeing services county of Pirkanmaa (2024). Retrieved January 17, 2024, from https://www.pirha.fi/en/web/english/about-us/about-the-wellbeing-services-county-of-pirkanmaa

  44. RISCC: Pirkanmaa hospital district (2020, 2024). Retrieved 31.1., 2024, from https://www.riscc-h2020.eu/about-riscc/partners/tauh/

  45. Fagerström, L.: Staffing Structures for Effectiveness in Person-Centred Care, pp. 119–130. Wiley, London (2017)

    Google Scholar 

  46. Frilund, M., Fagerström, L.: Oulu patient classification instrument within primary health care. Stud. Health Technol. Inform. 2009(146), 30–35 (2009)

    Google Scholar 

  47. Andersen, M.H., et al.: Testing reliability and validity of the Oulu patient classification instrument—the first step in evaluating the RAFAELA system in Norway. Open J. Nurs. 04(04), 303–311 (2014)

    Article  Google Scholar 

  48. Fagerström, L.: Expertvalidering av Oulu Patient Classification—En fas i utvecklingen av ett nytt system för vårdtyngds-klassificering, RAFAELA. Nord. J. Nurs. Res. 20(3), 15–21 (2000)

    Article  Google Scholar 

  49. Fagerström, L., et al.: Professional assessment of optimal nursing care intensity level. Scand. J. Caring Sci. 14(2), 97–104 (2000)

    PubMed  Google Scholar 

  50. Fagerström, L., et al.: Validation of a new method for patient classification, the Oulu Patient Classification. J. Adv. Nurs. 31(2), 481–490 (2000)

    Article  PubMed  Google Scholar 

  51. Frilund, M., Fagerström, L.: Validity and reliability testing of the Oulu patient classification: instrument within primary health care for the older people. Int. J. Older People Nurs. 4(4), 280–287 (2009)

    Article  PubMed  Google Scholar 

  52. Hustad, N.B., et al.: A qualitative study of manager experiences using the RAFAELA system. Open J. Nurs. 05(11), 1024–1032 (2015)

    Article  Google Scholar 

  53. Liljamo, P., et al.: Healthcare professionals’ views on the mutual consistency of the Finnish Classification of Nursing Interventions and the Oulu Patient Classification. Scand. J. Caring Sci. 30(3), 477–488 (2016)

    Article  PubMed  Google Scholar 

  54. Rauhala, A., Fagerström, L.: Are nurses’ assessments of their workload affected by non-patient factors? An analysis of the RAFAELA system. J. Nurs. Manag. 15(5), 490–499 (2007)

    Article  PubMed  Google Scholar 

  55. Zaranko, B., Sanford, N.J., Kelly, E., Rafferty, A.M., Bird, J., Mercuri, L., Sigsworth, J., Wells, M., Propper, C.: Nurse staffing and inpatient mortality in the English national health service: a retrospective longitudinal study. BMJ Qual. Saf. 1, 10 (2022). https://doi.org/10.1136/bmjqs-2022-015291

    Article  Google Scholar 

  56. Ropponen, A., Koskinen, A., Puttonen, S., Härmä, M.: Exposure to working-hour characteristics and short sickness absence in hospital workers: a case-crossover study using objective data. Int. J. Nurs. Stud. 91, 14–21 (2019). https://doi.org/10.1016/j.ijnurstu.2018.11.002

    Article  PubMed  Google Scholar 

  57. Grinza, E., Rycx, F.: The impact of sickness absenteeism on firm productivity: new evidence from Belgian matched employer–employee panel data. Ind. Relat. J. Econ. Soc. 59(1), 150–194 (2020)

    Google Scholar 

  58. Haegdorens, F., Van Bogaert, P., De Meester, K., Monsieurs, K.G.: The impact of nurse staffing levels and nurse’s education on patient mortality in medical and surgical wards: an observational multicentre study. BMC Health Serv. Res. 19(1), 1–9 (2019). https://doi.org/10.1186/s12913-019-4688-7

    Article  Google Scholar 

  59. Harrison, J.M., Aiken, L.H., Sloane, D.M., Carthon, J.M.B., Merchant, R.M., Berg, R.A., McHugh, M.D., Grossestreuer, A., Moskowitz, A., Edelson, D., Ornato, J., Berg, K., Peberdy, M.A., Churpek, M., Kurz, M., Starks, M.A., Chan, P., Girotra, S., Perman, S., Goldberger, Z.: In hospitals with more nurses who have baccalaureate degrees, better outcomes for patients after cardiac arrest. Health Aff. 38(7), 1087–1094 (2019). https://doi.org/10.1377/hlthaff.2018.05064

    Article  Google Scholar 

  60. Lasater, K.B., McHugh, M.D., Rosenbaum, P.R., Aiken, L.H., Smith, H.L., Reiter, J.G., Niknam, B.A., Hill, A.S., Hochman, L.L., Jain, S., Silber, J.H.: Evaluating the costs and outcomes of hospital nursing resources: a matched cohort study of patients with common medical conditions. J. Gen. Intern. Med. 36(1), 84–91 (2021). https://doi.org/10.1007/s11606-020-06151-z

    Article  PubMed  Google Scholar 

  61. Zheng, Q., Williams, C.S., Shulman, E.T., White, A.J.: Association between staff turnover and nursing home quality—evidence from payroll-based journal data. J. Am. Geriatr. Soc. 70(9), 2508–2516 (2022). https://doi.org/10.1111/JGS.17843

    Article  PubMed  Google Scholar 

  62. Musy, S.N., Endrich, O., Leichtle, A.B., Griffiths, P., Nakas, C.T., Simon, M.: The association between nurse staffing and inpatient mortality: a shift-level retrospective longitudinal study. Int. J. Nurs. Stud. 120, 103950 (2021). https://doi.org/10.1016/j.ijnurstu.2021.103950

    Article  PubMed  Google Scholar 

  63. Aiken, L.H., Cerón, C., Simonetti, M., Lake, E.T., Galiano, A., Garbarini, A., Soto, P., Bravo, D., Smith, H.L.: Hospital nurse staffing and patient outcomes. Rev. Méd. Clín. Las Condes 29(3), 322–327 (2018). https://doi.org/10.1016/J.RMCLC.2018.04.011

    Article  Google Scholar 

  64. Moyo, N., Jones, M., Dennis, S., Sharma, K., Gray, R.: The association between nursing skill mix and patient outcomes in a mental health setting: protocol for an observational feasibility study. Int. J. Environ. Res. Public Health (2022). https://doi.org/10.3390/ijerph19074357

    Article  PubMed  PubMed Central  Google Scholar 

  65. Zhang, Y., Martikainen, O., Pulli, P., Naumov, V.: Develo** a real-time process data acquisition system for automatic process measurement BT—grid and pervasive computing workshops. In: Teoksessa, R.M., Korhonen, T., Mutafungwa, E., Ovaska, E., Katasonov, A., Evesti, A., Ailisto, H., Quigley, A., Häkkilä, J., Milic-Frayling, N. & Riekki, J. (eds.). Springer, Berlin (2012)

  66. van Oostveen, C.J., et al.: Pre-implementation studies of a workforce planning tool for nurse staffing and human resource management in university hospitals. J. Nurs. Manag. 24(2), 184–191 (2016)

    Article  PubMed  Google Scholar 

  67. Castrén, L., Kauhanen, A., Kulvik, M., Kulvik-Laine, S., Lönnqvist, A., Maijanen, S., Martikainen, O., Palvalin, M., Peltonen, I., Ranta, P., Vuolle, M., Zhan, Y.: ICT ja palvelut—Näkökulmia tuottavuuden kehittämiseen. Helsinki: Taloustieto Oy (2013). http://www.etla.fi/wp-content/uploads/2012/09/B254.pdf

  68. Kauhanen, A., Kulvik, M., Kulvik, S., Maijanen, S., Martikainen, O., Ranta, P.: Resource allocation in health care processes: a case study 1. VSK 2420, 10 (2013)

    Google Scholar 

  69. Kotiranta, A., Kulvik, M., Maijanen, S., Seppälä, T.: Arvoketjut kustannusten näkökulmasta. Teoksessa Harsoja ja hallintoa—Terveysarvoketjujen anatomiaa, Kotiranta, A., Kulvik, M., Maijanen, S. & Seppälä, T. (eds.), 93–100. Helsinki: Taloustieto Oy (2016). https://www.etla.fi/julkaisut/harsoja-ja-hallintoa-terveysarvoketjujen-anatomiaa-2/

  70. Fagerström, L., Kinnunen, M., Saarela, J.: Nursing workload, patient safety incidents and mortality: an observational study from Finland. BMJ Open (2017). https://doi.org/10.1136/bmjopen-2017-016367

    Article  Google Scholar 

  71. Rauta, S., Salanterä, S., Vahlberg, T., Junttila, K.: Testing an instrument for assessing nursing intensity in perioperative settings: construct validity. Int. J. Nurs. Knowl. 28(4), 233–240 (2017). https://doi.org/10.1111/2047-3095.12117

    Article  PubMed  Google Scholar 

  72. Sutinen, T.: RafaelaTM-järjestelmän opcq-mittarin käyttö ja arviointi kehitysvammahuollossa. Itä-Suomen yliopisto UEF (2013)

  73. Alfra, T.A.O.F.L.A.R.A.: Special responsibility areas for medical care and hospital districts 2020, population 31.12.2018 (in Finnish). Kartta_Ervat_Sairaanhoitopiirit2020_0.pdf, ALFRA, The Association of Finnish Local and Regional Authorities (2020)

  74. Coelli, T.J., Prasada Rao, D.S., O’Donnell, C.J., Battese, G.E.: An Introduction to Efficiency and Productivity Analysis, 2nd edn. New York, Springer (2005)

    Google Scholar 

  75. Vähämäki, T., Kuusi, T., Laiho, M., Kulvik, M.: The road to productivity with automatization: Dialogue between the experienced and measured. Teoksessa Poutanen & Rouvinen (eds). Digital Work and the Platform Economy: Understanding Tasks, Skills, and Capabilities in the New Era. Routledge (2019)

  76. Bojke, C., Castelli, A., Grasic, K., Street, A.: Productivity growth in the English national health service from 1998/1999 to 2013/2014. Health Econ. 26, 547–565 (2017)

    Article  PubMed  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge the research funding of the Finnish Work Environment Fund, the Pirkanmaa Hospital District for the excellent cooperation in implementing the project, and the project steering group for their helpful comments.

Funding

This project was co-financed by the Finnish Work Environment Fund (Grant Agreement No. 200103), Etla and the Finnish Institute of Occupational Health.

Author information

Authors and Affiliations

  1. Etla Economic Research, Helsinki, Finland

    Tero Kuusi & Martti Kulvik

  2. Etlatieto Oy, Helsinki, Finland

    Martti Kulvik

  3. The Finnish Institute of Occupational Health, Helsinki, Finland

    Mikko Härmä & Annina Ropponen

Authors
  1. Tero Kuusi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Martti Kulvik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mikko Härmä
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Annina Ropponen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tero Kuusi.

Ethics declarations

Conflict of interest

The authors have no financial, proprietary or other conflict of interest in any material discussed in this article.

Ethical approval

The study protocol was designed and performed according to the principles of the Helsinki Declaration. This study was fully based on administrative register data that the hospital district had permitted the access. Although research using such data does not need to undergo review by an ethics committee according to Finnish legislation (Medical Research Act), this study had the ethical vetting performed and approved by the Ethical Review Board of Finnish Institute of Occupational Health (3/2020). None of the authors had access to any kind of identifying information. The data are not publicly available. All researchers participated in the analysis.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1: Burden and workload measurements

Implementation of the burden model

Our aim is to build a meaningful day-specific burden index from the classifications, which sufficiently considers the variation in the burden of different patients.

Even a metric that focuses on the main characteristics of the data can give a sufficiently detailed description of the workload. On the other hand, an advantage of a statistical tool is that it enables the flexible definition of different metrics and thus also the assessment of the adequacy of their detailedness. If simplified classifications that take into account the differences in work performance in different ways arrive at similar results on burden and its effects, it can be stated that the simplified metrics are sufficiently detailed to make general conclusions.

In our view, our main model (workload model 1) is the most natural starting point for processing our data, while we also discuss other options below. It separately classifies the burden of OPC main classes (1–3) for different treatment types. In addition, the effect on the workload of the sub-categories of the OPC classifications is evaluated separately.Footnote 12 On the other hand, treatments with no OPC classification are evaluated (only) according to their 7 different types.

Formally, the total effect of OPC-classified patients on the workload (without ward index) is

$$\mathop \sum \limits_{\begin{array}{*{20}c} {l = OPC\,main\,classification, } \\ {h = type\,of\,treatment} \\ \end{array} }^{OPC\,classified} \beta_{h,l} \, number_{l,h,t}^{\,} + \mathop \sum \limits_{\begin{array}{*{20}c} {l = OPC\,sub{\text{-}}classification} \\ {k = OPC\,category} \\ \end{array} }^{OPC\,classified} \beta_{k,l} \,number_{l,k,t}^{\,}$$

The individual regression coefficient (\(\beta\)) tells how much more (less in the case of a negative coefficient) the consideration of a certain feature requires human resources (in hours) compared to the reference category, where all other factors (by the other reference criteria used) are the same.

It is worth noting that in the first sum, the terms are specific to the main class and the treatment type. Presented in this way, for example, a patient whose treatment type is “ward treatment period”, the main category of OPC burden is 2 and the OPC sub-classifications are B in all categories, is estimated to consume the following amount of working hour \(\beta_{ward\,treatment\,period,\,2} + \sum_{k = 1}^6 \beta_{B,k}\), where the coefficients \(\beta\) of the different criteria indicate the effect of one such additional patient on the patient load.Footnote 13

Workload model 1 (and Model 2 introduced below as a robustness check) is limited to wards where more than half of the patients have received an OPC classification. The average burden of the first, last and one-day treatment periods, annual fixed cost effects and ward-specific fixed effects are also controlled in all the models.

Burden and workload measurements

When the burden model that evaluates the work input has been calculated for the entire patient population, it can be used to estimate the ward’s resource demand (service activity) in relation to the actual resource used (the number of hours worked by nurses). Based on the calculation, an index is created that measures the workload in relation to the average. It gets a value of 1 when the workload is at an average level based on the patient load. A value of 2 means that the workload is twice the average, and a value of 0.5 means that the workload is half of the average.

When defining the burden index, a balance must be struck between sufficient detail and excessive complexity. The model must have so many factors differentiating burden that the key factors affecting burden are considered. At the same time, overcomplicating the model must be avoided: The classification of burden can also be too detailed, if it divides tasks that are equally demanding into different categories and at the same time makes the use of the model statistically burdensome.

An example sheds light on how the increase in the number of patient classification methods can cause problems in terms of statistical modelling. The burden of treatment can be assumed to be influenced by the type of treatment and the (OPC) burden class estimated for the treatment. In our data, there are seven types of treatment and three main burden classes (1–3). Classified in this way, there are 21 different treatments. In addition to this, OPC burden is divided into six different burden sub-categories. There are 46 = 4096 different combinations on intensity-of-care classes in the data, and their burden may vary in different types of care. Therefore, it is not possible to evaluate the burden of each different combination of features.

All in all, the data we used offered opportunities for detailed analysis. The main model we used (model 1) classified the patient population into different burden categories by type of treatment, using the main categories of the Oulu patient classification (OPC). From the data, an average treatment burden was calculated separately for different patient categories. In addition, the effect on the burden of the sub-categories of the OPC classifications was evaluated separately. On the other hand, treatments with no OPC classification were evaluated (only) according to their treatment type.

Estimates of burden in the data

We first look at the estimates of resource utilisation. In the following, we mainly focus on model 1, where productivity was evaluated according to treatment type and OPC burden class, and individual OPC sub-categories were controlled. See, “Alternative Specification of Treatment Burden” for comparison with an alternative specification.

The burden weights are described in more detail in the following, by evaluating nurses’ time use according to a statistical model—however, for the sake of simplicity, we present in Table 

Table 7 Resource use (total working hour of the staff in relation to the average) in different types of care and OPC main intensity-of-care classes.
Full size table

7 estimates of statistical model for all ward types together. This gives an average estimate of the effects of different classifications on time use. The presented coefficients are estimates of the effect of adding a specific type of patient on time use in relation to the average.

Based on Table 7, there are significant differences in time use between different treatment types. Patients cause the biggest load in day surgery and the smallest in outpatient visits. The higher the OPC intensity-of-care class of the treatment, the higher the average treatment burdens for it are. In all cases, however, there were large differences between events falling in the same category, so the statistical uncertainty of the average time use estimates is quite large, and we emphasize that this uncertainty needs to be taken into account when making statistical inferences on the implications of workload. It should be noted that there were no treatment periods of classes 2 and 7 in the data.

The effects of different OPC sub-categories on time use are described in Table 

Table 8 Resource use in relation to the average, effect of OPC sub-classes, with OPC main class and treatment type being controlled.
Full size table

8. Based on this, especially the increase in the intensity-of-care class in the areas of care planning and coordination; nutrition and medication treatment; and hygiene and special activities increase the required nursing resources relative to the average. It is noteworthy that, in category 5 (activity, slee** and rest) and 2 (respiration, circulation and symptoms of illness), the burden of the intensity-of-care class is strongly positively correlated with the burden of the other sub-criteria.

This may partly explain why the increase in the burden of treatment does not appear as an increase in the estimated amount of work when other factors are controlled. Again, the effect of different classes on time use varies a lot, which can be seen in the rather large confidence intervals of the estimates.

Regarding other features, it should be mentioned that the first few and last few days of treatment are more demanding (marginally increasing the number of hours) and, on the other hand, treatments lasting only one day are less demanding (marginally decreasing the number of hours).

Uncertainty of the measures

Figure 

Fig. 6
figure 6

Workload at the monthly level (black line) and the statistical 95% confidence interval related to the estimate (grey lines), ward ID pseudonymised. Note: Only wards with more than 1000 daily observations and more than 10 employees have been selected for the graph

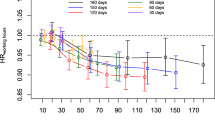
Full size image

6 examines the uncertainty related to the workload estimates in the different months of the data on average. Based on the estimates, it can be stated that the estimates of the workload do vary due to the uncertainty of the data, but on the other hand, the model provides in any case a fairly reliable picture of the burden of different periods. The conclusion is based on the fact that the confidence intervals of the workload estimates are quite moderate.

Alternative specifications of treatment burden

In the second version (burden model 2), the numbers of patients are added up per OPC sub-classification category and treatment type. The effects of different OPC sub-classifications within different treatment types are then evaluated separately.

$$\mathop \sum \limits_{\begin{array}{*{20}c} {l = OPC\,sub{\text{-}}classification} \\ {k = OPC\,category} \\ {h = type\,of\,treatment} \\ \end{array} }^{OPC\,classified} \beta_{k,l,h} \,number_{l,k,t}^{\,}$$

This time, each coefficient distinguishes the patient based on three different characteristics. For example, the same patient whose treatment type is “ward treatment period”, the main OPC burden class is 2 and the OPC sub-classifications are B in all categories, is estimated to consume the following amount of working hour:

$$\mathop \sum \limits_{k = 1}^6 \beta_{B,k,t}$$

When evaluated in this way, a better understanding of the associations of the different subcategories to the patient’s burden in different types of treatment is obtained. On the other hand, the possible combined effects of the OPC sub-classifications on the burden are not taken into account. If the sub-categories of the OPC classification change again like in the benchmark example, so that category 1 is now A and 2 is C, the impact on the workload in this model is:

$$\left( {\beta_{A,1,t} - \beta_{B,1,t} } \right) + \left( {\beta_{C,2,t} - \beta_{B,2,t} } \right)$$

The effects of changes in OPC sub-classifications are thus specific to the type of treatment, but a change in the burden of one sub-category is not assumed to affect the change in burden of another sub-category.Footnote 14

By utilising different metrics, it is possible to assess whether the differences presented above are essential in evaluating the workload. If they are not, the results from metrics using different classifications will be similar.

In models 1 (benchmark) and 2, it should, furthermore, be emphasised that, while the patient classification is not available in all cases, the type of treatment is. In these cases, the average treatment-type-specific cost, with no OPC classification, is evaluated.

$$\mathop \sum \limits_{h = type\,of\,treatment}^{Not\,OPC\,classified} \gamma_h lkm_{h,t}$$

In these cases, the patient’s burden is simply a coefficient to be calculated on average for the missing observations \(\gamma_h .\)Footnote 15

Workload estimates with the help of different models

Finally, we compared the workloads measured in different ways. Figure 

Fig. 7
figure 7

Workload at the daily level, comparison between different models (the green line is workload model 1 and the red dotted line is workload model 2). The ward ID is pseudonymised. Notes: Only wards with more than 1000 daily observations and more than 10 employees have been selected for the graph

Full size image

7 shows and compares assessments according to workload models 1 and 2. Overall, the estimates are very similar, although the workload estimates clearly deviate in the case of one ward. The estimates produced by workload model 2 (anonymised ward number 61) are quite large, even on average, which suggests that model 1 would produce more realistic estimates of the workload.Footnote 16

One natural way of approaching the similarity of the metrics is to evaluate the correlations between them. Workload metrics 1 and 2 are quite strongly correlated with each other. In the data as a whole the correlation is 0.69. In those wards where there are more than 1000 daily observations and an average of more than 10 employees, the correlation is 0.65. Excluding the individual ward (61) with a more unclear evaluation, the correlation is very high, 0.86.

All in all, based on the findings, focusing on one metric (workload model 1) seems justified. Although the metrics do not give the exact same results, their strong correlation means that they have very similar implications for research on the associations between general workload and work characteristics.

Appendix 2: Working hour characteristics and short sickness absences

We separately examined the associations of different working hour characteristics to the risk of sickness absence and to the workload. Cross-effects of the workload and features of working hour were added as explanatory factors to the model. They were used to explain the frequency of short sickness absences.

$$\begin{aligned} short\,sickness\,absence_{h,t} & = \mathop \sum \limits_{k = 1}^n \alpha_k \,workload_{k,i,t - k} + \mathop \sum \limits_{k = 1}^n \alpha_k^r \,workload_{i,t - 1} cross\,variables_{k,h,t} \\ & \quad + \gamma *\,control\,variables_t + \epsilon_h + \epsilon_t + \epsilon_{h,t} \,\left( {model \,3} \right) \\ \end{aligned}$$

However, it turned out that the working hour characteristics, together with the workload, are not associated to an increased or decreased risk of sickness absences, at least in any statistically significant way. Table

Table 9 Cross-effects of the workload and features of working hour.
Full size table

9 shows that none of the cross-effect terms (\(\alpha_k^r\) in statistical Model 3) deviate from zero at the 95 per cent confidence level. This means that no single working hour feature increases the effect of workload on the risk of sickness absence in a statistically detectable way.

Based on the previous section, it seems more like certain working hour characteristics are directly associated to the amount of workload. But no clear evidence was found in this analysis of their joint effects on short sickness absences. At the same time, it must be stated that the scope of the data does not allow for very detailed analyses and, therefore, associations cannot be excluded based on the results either.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuusi, T., Kulvik, M., Härmä, M. et al. Workload and short sickness absences in a cohort of Finnish hospital employees. Eur J Health Econ (2024). https://doi.org/10.1007/s10198-024-01698-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10198-024-01698-8

Keywords

JEL Classification

Search

Navigation