Efficient joint object matching via linear programming

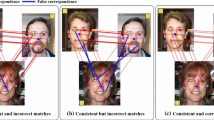
Abstract

Joint object matching, also known as multi-image matching, namely, the problem of finding consistent partial maps among all pairs of objects within a collection, is a crucial task in many areas of computer vision. This problem subsumes bipartite graph matching and graph partitioning as special cases and is NP-hard, in general. We develop scalable linear programming (LP) relaxations with theoretical performance guarantees for joint object matching. We start by proposing a new characterization of consistent partial maps; this in turn enables us to formulate joint object matching as an integer linear programming (ILP) problem. To construct strong LP relaxations, we study the facial structure of the convex hull of the feasible region of this ILP, which we refer to as the joint matching polytope. We present an exponential family of facet-defining inequalities that can be separated in strongly polynomial time, hence obtaining a partial characterization of the joint matching polytope that is both tight and cheap to compute. To analyze the theoretical performance of the proposed LP relaxations, we focus on permutation group synchronization, an important special case of joint object matching. We show that under the random corruption model for the input maps, a simple LP relaxation, that is, an LP containing only a very small fraction of the proposed facet-defining inequalities, recovers the ground truth with high probability if the corruption level is below 40%. Finally, via a preliminary computational study on synthetic data, we show that the proposed LP relaxations outperform a popular SDP relaxation both in terms of recovery and tightness.

Appendix

1.1 Facetness for block consistency inequalities

Proof of Proposition 8

Without loss of generality, we prove for any nonempty $D_1, D_2, D_3 \subseteq [d]$ with $|D_1|+|D_2| > |D_3|$, the following defines a facet of the joint matching polytope ${\mathcal {C}}_{n,d}$:

$$\begin{aligned} \sum _{l \in D_3}{\left( \sum _{t\in D_1}{X_{lt}(1,2)}+\sum _{q\in D_2}{X_{lq}(1,3)}\right) }-\sum _{t \in D_1}{\sum _{q \in D_2}{X_{tq}(2,3)}} \le |D_3|. \end{aligned}$$

(70)

We start by identifying the set of consistent partial maps in ${\mathcal {C}}_{n,d}$ that satisfy inequality (70) tightly. Subsequently, we show that any nontrivial valid inequality $\alpha X \le \beta$ for ${\mathcal {C}}_{n,d}$ that is satisfied tightly at all such maps coincides with (70) up to a positive scaling. Since ${\mathcal {C}}_{n,d}$ is full dimensional, this in turn implies that inequality (70) defines a facet of ${\mathcal {C}}_{n,d}$.

A consistent partial map is binding for inequality (70), if for every $l \in D_3$, there exists $e_l \in {\mathcal {M}}_X$ with $1_l \in e_l$ satisfying one of the following conditions:

• (i) $2_t \in e_l$ for some $t \in D_1$ and $3_q \notin e_l$ for all $q \in D_2$,

• (ii) $2_t \notin e_l$ for all $t \in D_1$ and $3_q \in e_l$ for some $q \in D_2$,

• (iii) $2_t \in e_l$ for some $t \in D_1$ and $3_q \in e_l$ for some $q \in D_2$.

Now consider a consistent partial map ${\mathcal {M}}^1_X$ satisfying conditions (i) or (ii) above for all $l \in D_3$ such that for some $t' \in D_1$ we have $2_{t'} \notin e_l$ for all $l \in D_3$. Notice that such a consistent partial map exists since by assumption $|D_1| +|D_2| > |D_3|$. Moreover, suppose that ${\mathcal {M}}^1_X$ contains no matched pairs other than those required by conditions (i)–(ii), i.e., ${\mathcal {M}}^1_X = \{e_l,\; l \in D_3\}$ with $|e_l|= 2$ for all $l \in D_3$. Next consider another consistent partial map obtained from ${\mathcal {M}}^1_X$ by replacing a matched pair of the form $(1_{{\hat{l}}},2_{{\hat{t}}})$ for some ${\hat{t}} \in D_1$ and ${\hat{l}} \in D_3$ by $(1_{{\hat{l}}},2_{t'})$, where $t' \in D_1$ is the index defined above. Notice that this flip** operation results in a consistent partial map that is also binding for (70). Substituting these two partial maps in $\alpha X = \beta$ yields $\alpha _{{\hat{l}} {\hat{t}}}(1,2) =\alpha _{{\hat{l}} t'}(1,2)$. Using a similar line of arguments for all possible consistent partial maps satisfying conditions (i) or (ii) for all $l \in D_3$ together with $2_{t'} \notin e_l$ for some $t' \in D_1$ ($3_{t'} \notin e_l$ for some $t' \in D_2$) for all $l \in D_3$, we conclude that for each $l \in D_3$, we have

$$\begin{aligned} \alpha _{lt}(1,2) = \alpha _{lq}(1,3), \quad \forall t \in D_1, \; \forall q \in D_2. \end{aligned}$$

(71)

Next consider a consistent partial map ${\mathcal {M}}^2_X$ satisfying conditions (i) or (ii) above for all $l \in {\mathcal {D}}_3 \setminus \{{\hat{l}}\}$ and suppose that for ${\hat{l}}$ condition (iii) is satisfied, i.e., $e_{{\hat{l}}} = (1_{{\hat{l}}}, 2_{{\hat{t}}}, 3_{{\hat{q}}})$ for some ${\hat{t}} \in D_1$ and ${\hat{q}} \in D_2$. Consider a second consistent partial map satisfying conditions (i) or (ii) above for all $l \in {\mathcal {D}}_3 \setminus \{{\tilde{l}}\}$ where ${\tilde{l}} \ne {\hat{l}}$ and suppose that for ${\tilde{l}}$ condition (iii) is satisfied with $e_{{\tilde{l}}} = (1_{{\tilde{l}}}, 2_{{\hat{t}}}, 3_{{\hat{q}}})$. In addition, suppose that in both these maps, no additional matched pairs other than those required by conditions (i)–(iii) exist. Substituting these two maps in $\alpha X = \beta$ and using (71) yield $\alpha _{{\hat{l}} {\hat{t}}}(1,2) = \alpha _{{\tilde{l}} {\hat{t}}}(1,2)$ and $\alpha _{{\hat{l}} {\hat{q}}}(1,3) = \alpha _{{\tilde{l}} {\hat{q}}}(1,3)$. Using a similar line of arguments for all possible pairs of partial maps satisfying assumptions above, we obtain:

$$\begin{aligned} \alpha _{lt}(1,2) = \alpha _{lq}(1,3) = \frac{\beta }{|D_3|}, \quad \forall t \in D_1, \; \forall q \in D_2, \; \forall l \in D_3. \end{aligned}$$

(72)

Moreover, substituting the partial map corresponding to ${\mathcal {M}}^2_X$ in $\alpha X = \beta$ and using (72) we obtain $\alpha _{{\hat{t}} {\hat{q}}}(2,3) = -\beta /|D_3|$. It then follows that

$$\begin{aligned} \alpha _{tq}(2,3) = -\frac{\beta }{|D_3|}, \quad \forall t \in D_1, \; \forall q \in D_2. \end{aligned}$$

(73)

Next consider a consistent partial map ${\mathcal {M}}^3_X$ satisfying conditions (i) or (ii) above for all $l \in {\mathcal {D}}_3$ of the form ${\mathcal {M}}^3_X = \{e_l: l\in D_3\}$ with $|e_l| = 2$ for all $l \in D_3$. Construct another consistent partial map of the form ${\mathcal {M}}^3_X \cup \{(i_t, j_q)\}$ for some $(i,j,t,q) \in {\mathcal {Q}}$, where

$$\begin{aligned} Q :&= \left\{ (i,j,t,q): 4 \le i < j \le n, t \in [d], q \in [d]\right\} \\&\cup \Big \{(1,j,t,q): j \ge 4, t \in [d] \setminus D_3, q \in [d]\Big \}\\&\cup \Big \{(2,j,t,q): 4 \le j \le n, t \in [d] \setminus D_1, q \in [d]\Big \} \\&\cup \Big \{(3,j,t,q): 4 \le j \ge n, t \in [d] \setminus D_2, q \in [d]\Big \}\\&\cup \Big \{(1,2,t,q): t \in [d] \setminus D_3, q \in [d] \setminus D_1\Big \} \\&\cup \Big \{(1,3,t,q): t \in [d] \setminus D_3, q \in [d] \setminus D_2\Big \}\\&\cup \Big \{(2,3,t,q): t \in [d] \setminus D_1, q \in [d] \setminus D_2\Big \}. \end{aligned}$$

Substituting these two partial maps in $\alpha X = \beta$ yields

$$\begin{aligned} \alpha _{tq}(i,j) = 0, \quad \forall (t,q,i,j) \in {\mathcal {Q}}. \end{aligned}$$

(74)

Consider the consistent partial map ${\mathcal {M}}^3_X$ defined above with the additional assumption that for some ${\hat{t}} \in D_1$ (resp. ${\hat{q}} \in D_2$), we have $(1_l, 2_{\hat{t}}) \notin {\mathcal {M}}^3_X$ (resp. $(1_l, 3_{\hat{q}}) \notin {\mathcal {M}}^3_X$) for all $l \in D_3$. Notice that such a partial map always exists since by assumption $|D_1|+|D_2| > |D_3|$. Construct another consistent partial map of the form:

• ${\bar{{\mathcal {M}}}}^3_X = {\mathcal {M}}^3_X \cup \{(1_{{\hat{l}}}, 2_{{\hat{t}}})\}$ (resp. ${\bar{{\mathcal {M}}}}^3_X ={\mathcal {M}}^3_X \cup \{(1_{{\hat{l}}}, 3_{{\hat{q}}})\}$) for some ${\hat{l}} \notin D_3$. Substituting ${\mathcal {M}}^3_X, {\bar{{\mathcal {M}}}}^3_X$ in $\alpha X = \beta$ gives $\alpha _{{\hat{l}} {\hat{t}}}(1,2) =0$ (resp. $\alpha _{{\hat{l}} {\hat{t}}}(1,3) =0$). Using a similar line of arguments for all possible partial maps satisfying the assumptions above, we obtain

  $$\begin{aligned} \alpha _{lt}(1,2) = \alpha _{lq}(1,3) = 0, \quad \forall l \in [d] \setminus D_3, \forall t \in D_1, \forall q \in D_2. \end{aligned}$$

  (75)

• ${\bar{{\mathcal {M}}}}^3_X = {\mathcal {M}}^3_X \cup \{(2_{{\hat{t}}}, j_s)\}$ (resp. ${\bar{{\mathcal {M}}}}^3_X ={\mathcal {M}}^3_X \cup \{(3_{{\hat{q}}}, j_s)\}$ ) for some $4 \le j \le n$ and some $s \in [d]$. Substituting ${\mathcal {M}}^3_X, {\bar{{\mathcal {M}}}}^3_X$ in $\alpha X = \beta$ gives $\alpha _{{\hat{t}} s }(2,j) =0$ (resp. $\alpha _{{\hat{q}} s}(3, j) =0$). Using a similar line of arguments for all possible partial maps satisfying the assumptions above, we obtain

  $$\begin{aligned} \alpha _{ts}(2,j) \!=\! \alpha _{qs}(3,j) = 0, \quad \forall 4 \le j \le n, \forall t \in D_1, \forall q \in D_2, \forall s \in [d].\qquad \end{aligned}$$

  (76)

• ${\bar{{\mathcal {M}}}}^3_X = {\mathcal {M}}^3_X \cup \{(2_{{\hat{t}}}, 3_q)\}$ for some $q \in [d] \setminus D_2$ (resp. ${\bar{{\mathcal {M}}}}^3_X = {\mathcal {M}}^3_X \cup \{(2_t, 3_{{\hat{q}}})\}$ for some $t \in [d] \setminus D_1$). Substituting ${\mathcal {M}}^3_X, \bar{\mathcal {M}}^3_X$ in $\alpha X = \beta$ gives $\alpha _{{\hat{t}} s }(2,j) =0$ (resp. $\alpha _{{\hat{q}} s}(3, j) =0$). Using a similar line of arguments for all possible partial maps satisfying the assumptions above, we obtain

  $$\begin{aligned} \alpha _{tq}(2,3) = 0, \quad \forall t \in [d]\setminus D_1, q \in D_2 \; \textrm{or} \; \forall t \in D_1, q \in [d] \setminus D_2. \end{aligned}$$

  (77)

Consider a consistent partial map ${\mathcal {M}}^4_X$ satisfying conditions (i) or (ii) above for all $l \in {\mathcal {D}}_3$ of the form ${\mathcal {M}}^4_X = \{e_l: l\in D_3\}$ with $|e_l| = 2$ for all $l \in D_3$. Consider some ${\hat{l}} \in D_3$ for which $e_{{\hat{l}}} = (1_{{\hat{l}}}, 2_{{\hat{t}}})$ for some ${\hat{t}} \in D_1$ (resp. $e_{{\hat{l}}} = (1_{{\hat{l}}}, 3_{{\hat{q}}})$ for some ${\hat{q}} \in D_2$). Construct another consistent partial map of the form

• ${\bar{{\mathcal {M}}}}^4_X = {\mathcal {M}}^4_X \cup \{(1_{{\hat{l}}}, 3_{{\hat{q}}}), (2_{{\hat{t}}}, 3_{{\hat{q}}})\}$ for some ${\hat{q}} \in [d] \setminus D_2$ (${\bar{{\mathcal {M}}}}^4_X = {\mathcal {M}}^4_X \cup \{(1_{{\hat{l}}}, 2_{{\hat{t}}}), (2_{{\hat{t}}}, 3_{{\hat{q}}})\}$ for some ${\hat{t}} \in [d] \setminus D_1$). Substituting these two partial maps in $\alpha X = \beta$ and using (77) we obtain $\alpha _{{\hat{l}} {\hat{t}}}(1,2) = 0$ (resp. $\alpha _{{\hat{l}} {\hat{q}}}(1,3) = 0$). More generally it can be checked that

  $$\begin{aligned} \alpha _{lt}(1,2) = \alpha _{lq}(1,3) = 0, \quad \forall l \in D_3, \forall t \in [d] \setminus D_1, \forall q \in [d] \setminus D_2. \end{aligned}$$

  (78)

• ${\bar{{\mathcal {M}}}}^4_X = {\mathcal {M}}^4_X \cup \{(1_{{\hat{l}}}, j_s), (2_{{\hat{t}}}, j_s)\}$ (resp. ${\bar{{\mathcal {M}}}}^4_X = {\mathcal {M}}^4_X \cup \{(1_{{\hat{l}}}, j_s), (3_{{\hat{q}}}, j_s)\}$) for some $4 \le j \le n$ and $s \in [d]$. Substituting these two partial maps in $\alpha X = \beta$ and using (76) we obtain $\alpha _{{\hat{l}} s}(1,j) = 0$. More generally, it can be checked that

  $$\begin{aligned} \alpha _{ls}(1,j) = 0, \quad \forall 4 \le j \le n, \forall l \in D_3, \forall s \in [d]. \end{aligned}$$

  (79)

From (70)–(79) it follows that the inequality $\alpha X \le \beta$ can be equivalently written as

$$\begin{aligned} \frac{\beta }{|D_3|} \left( \sum _{l \in D_3}{\left( \sum _{t\in D_1}{X_{lt}(1,2)}+\sum _{q\in D_2}{X_{lq}(1,3)}\right) }-\sum _{t \in D_1}{\sum _{q \in D_2}{X_{tq}(2,3)}}\right) \le \beta . \end{aligned}$$

Since $\alpha X \le \beta$ is nontrivial and valid, we have $\beta > 0$ and this completes the proof.

1.2 Size inequalities

In this section, we assume that an upper bound ${\hat{m}}$ on the size of the universe is available and we utilize ${\hat{m}}$ to improve our proposed LP relaxation. As in Sect. 2, consider a collection of n objects each consisting of $d_i$, $i \in [n]$ elements; that is, we have a total number of ${\bar{d}} = \sum _{i \in [n]}{d_i}$ elements. Let ${\mathcal {N}}$ denote the set consisting of all these elements, i.e., ${\mathcal {N}}= \cup _{i \in [n]}{\cup _{t \in [d_i]}{i_t}}$. Define $d_{\min } = \min _{i \in [n]} d_i$ and $d_{\max } = \max _{i \in [n]} d_i$, where we assume $d_{\max } \ge 2$. Let ${\hat{m}} \in \{d_{\max }, \ldots ,{\bar{d}}-1\}$. Notice that ${\hat{m}}= {\bar{d}}$ is a trivial upper bound and cannot be exploited to improve the relaxation.

Proposition 10

Consider a subset ${\mathcal {N}}' \subset {\mathcal {N}}$ of cardinality ${\hat{m}} + 1$. Then the following inequality is valid for the feasible region of Problem (IP):

$$\begin{aligned} \sum _{1 \le i < j \le n}{\sum _{\begin{array}{c} t \in [d_i] q \in [d_j]: \\ i_t, j_q \in {\mathcal {N}}' \end{array}}{X_{tq}(i,j)}} \ge 1, \end{aligned}$$

(80)

where $i_t$ and $j_q$ denote the t-th element of object ${\mathcal {S}}_i$ and the q-th element of object ${\mathcal {S}}_j$, respectively.

Proof

To see the validity of inequality (80), suppose that $X_{tq}(i,j) = 0$ for all $i_t, j_q \in {\mathcal {N}}'$. Since by assumption $|{\mathcal {N}}'| = {\hat{m}} + 1$, it then follows that the size of the universe is at least ${\hat{m}} +1$, which contradicts with the assumption that ${\hat{m}}$ is an upper bound on the size of the universe. $\square$

Henceforth, we refer to inequalities of the form (80) for all ${\mathcal {N}}' \subset {\mathcal {N}}$ as size inequalities. The following example demonstrates that size inequalities can tighten the proposed LP relaxation.

Example 6

Let $n =3$ and $d_1 = d_2 = d_3 =2$; moreover, suppose that ${\hat{m}} = 3$. Then it can be checked that the following is feasible for Problem (LPF):

$$\begin{aligned} X(1,2) = \begin{pmatrix} 0 &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix}, \qquad X(1,3) = \begin{pmatrix} 0 &{} \quad 0 \\ 0 &{}\quad 1 \end{pmatrix}, \qquad X(2,3) = \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix}. \end{aligned}$$

(81)

Now consider a size inequality obtained by letting ${\mathcal {N}}'=\{1_1, 1_2, 2_1, 2_2\}$ in inequality (80):

$$\begin{aligned} X_{11}(1,2)+X_{12}(1,2)+X_{21}(1,2)+X_{22}(1,2) \ge 1. \end{aligned}$$

Substituting (81) in the above inequality yields $0+0+0+0 \not \ge 1$.

Next, suppose that ${\hat{m}} = 4$ and consider the point:

$$\begin{aligned} X(1,2) = \begin{pmatrix} 0 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}, \qquad X(1,3) = \begin{pmatrix} 0 &{} \quad 0 \\ 0 &{}\quad 0 \end{pmatrix}, \qquad X(2,3) = \begin{pmatrix} 0 &{} \quad 0 \\ 0 &{}\quad 0 \end{pmatrix}. \end{aligned}$$

(82)

Again, it can be checked that (82) is feasible for Problem (LPF). Consider now the size inequality obtained by letting ${\mathcal {N}}'=\{1_1, 2_1, 2_2,3_1,3_2\}$:

$$\begin{aligned}{} & {} X_{11}(1,2)+ X_{12}(1,2)+X_{11}(1,3)+ X_{12}(1,3)+X_{11}(2,3)+ X_{12}(2,3)\\{} & {} \quad +X_{21}(2,3)+ X_{22}(2,3)\ge 1. \end{aligned}$$

Substituting (82) in the above inequality yields $0+0+0+0+0+0+0+0 \not \ge 1$.

Remark 3

Let us revisit the graph partitioning problem described in Remark 1; namely, the problem of partitioning the nodes of a graph into at most K subsets [9]. Let ${\tilde{N}}$ denote a subset of [n] with $|{\tilde{N}}| = K +1$. Then the clique inequality associated with ${\tilde{N}}$ is defined as

$$\begin{aligned} \sum _{i,j \in {\tilde{N}}: i < j}{y_{ij}} \ge 1. \end{aligned}$$

(83)

Now, let $t \in [d_{\min }]$ and consider a size inequality (80) with ${\mathcal {N}}' = \{i_t: i \in I \subseteq [n]\}$, where $|I| = {\hat{m}} + 1$; that is, the inequality:

$$\begin{aligned} \sum _{i,j \in I: i < j}{X_{tt}(i,j)} \ge 1. \end{aligned}$$

(84)

Comparing (83) and (84), it follows that for a particular type of ${\mathcal {N}}'$, the corresponding size inequalities have the same form as clique inequalities. However, we would like to remark that while a clique inequality (83) associated with a clique of size r contains $\left( {\begin{array}{c}r+1\\ 2\end{array}}\right)$ variables, a size inequality (84) associated with ${\mathcal {N}}'$ of cardinality r may contain different number of variables.

For instance, let $n = 5$, $d_i = 3$ for all $i \in \{1,\ldots ,5\}$, and suppose that ${\hat{m}} = 4$. Then letting ${\mathcal {N}}'=\{1_1,1_2,1_3, 2_1, 2_2\}$ in (80), we obtain the size inequality

$$\begin{aligned} X_{11}(1,2)+ X_{12}(1,2)+X_{21}(1,2)+ X_{22}(1,2)+X_{31}(1,2)+ X_{32}(1,2) \ge 1, \end{aligned}$$

consisting of six variables, while letting ${\mathcal {N}}'=\{1_1,2_1, 3_1, 4_1,4_2\}$, we obtain a size inequality

$$\begin{aligned}&X_{11}(1,2)+ X_{11}(1,3)+X_{11}(1,4)+ X_{12}(1,4)+X_{11}(2,3)+ X_{11}(2,4)+X_{12}(2,4)\\&\quad +X_{11}(3,4)+X_{12}(3,4) \ge 1, \end{aligned}$$

consisting of nine variables.

Hence size inequalities (80) can be considered a generalization of clique inequalities for joint object matching. It is well-known that the separation problem over clique inequalities (83) is NP-hard [16]. Various heuristics for separating clique inequalities have been proposed in the literature [16] and similar ideas could be developed to efficiently separate over size inequalities. However, such a computational study is beyond the scope of this paper.

Remark 4

Consider the following variant of joint object matching: find a collection of consistent partial maps $X(i,j) \in \{0,1\}^{d_i\times d_j}$ for all $1 \le i < j \le n$ corresponding to a universe of at most ${\hat{m}}$ elements so as to minimize (6). It can be checked that this problem can be equivalently solved by solving the ILP obtained by adding all size inequalities (80) to Problem (IP).