1 Introduction

The last few decades have seen significant advances in computing power, as well as increased pressure to optimise the efficiency of all aspects of production processes and reduce associated costs. This has naturally led to a significant increase in interest in production planning techniques, both in industry and academia.

In general terms, production planning is a decision-making process aimed at determining when, where, how, and what to produce from a given set of products that have defined characteristics and requirements. This process is carried out by managing a set of finite resources and is in most cases subject to time constraints from the outset, as indicated in the reference (Floudas and Lin 2004).

Mathematical programming, especially Mixed Integer Linear Programming (MILP), is widely used for production scheduling processes due to its rigour, versatility, and extensive modelling capabilities (Floudas and Lin 2005). Models assessing scheduling for a single station are commonly encountered in this field, mainly because they are highly applicable in three primary scenarios. The initial challenge lies with intricate multi-stage problems that can be deconstructed into simpler, self-reliant, or loosely connected single-stage problems (Pinto and Grossmann 1995); thus, handling production planning in a modular manner. The second application area is in systems where a station acts as a significant bottleneck. In such cases, production planning for the particular station is critical for the entire system. Consequently, this planning can be extended to the remaining stations (Díaz-Ramírez and Huertas 2018; Elekidis et al. 2019; Marchetti and Cerdá 2009a). Ultimately, it is relevant to issues with a solitary station (Aguirre and Papageorgiou 2018; Méndez and Cerdá 2002).

When develo** mathematical models, one of the initial decisions to consider is how time should be represented (Floudas and Lin 2005; Sung and Maravelias 2009). Consequently, three primary classes of MILP models are identified: those formulated with a complete planning horizon in discrete time, those formulated in continuous time, and hybrid models. Despite the extensive literature dealing with such problems, there are no studies that analyse, for the same problem, the response of a continuous model and that of a discrete model.

Acknowledging the relevance of such problems and the existing gap in the literature to date, this study will introduce two MILP mathematical models to solve the same single station problem, one with continuous time representation and the other with discrete representation. Both models will be tested using a database containing actual time estimates from a factory with these characteristics. The results of this experiment will be presented and compared.

The structure of this paper is as follows. Section 2 defines the core problem and situates it within the existing literature. Section 3 presents the continuous and discrete models and is further divided into two subsections, one dedicated to each model. Section 4 presents a comprehensive analysis of the results obtained by applying these models and draws important conclusions. Finally, the last section provides a list of all references cited throughout this document.

2 Problem definition

As noted previously, there exist three categories of models that are established on the basis of representative time: continuous, discrete, and hybrid models. In the continuous formulation, the planning horizon is partitioned as a component of the optimisation process, allowing the placement of tasks at any point in the timeline (Roslöf et al. 2001; Harjunkoski and Grossmann 2002; He et al. 2017). On the contrary, discrete models are founded on dividing the timeline into different intervals or time units of generally equal size (Liu et al. 2010b; Lee et al. 2002; Mouret et al. 2011). The model is constrained to schedule tasks at specific time points due to this discretization. Less frequently, there are mixed formulations in which discrete periods, such as weeks, are already predetermined within the temporal horizon (Aguirre and Papageorgiou 2018; Liu et al. 2010a; Chen et al. 2008). However, in each of these periods, there is a continuous representation in use. However, according to the review of the literature on MILP models of a single station conducted by Muñoz-Díaz et al. (2022), there are no articles that develop continuous and discrete representations to solve the same problem. This study presents and encodes both versions for future comparison.

Once the difference in time representation has been established, the remaining characteristics of the issue and models are specified. This will be identical for both the continuous and the discrete versions. It is essential to note that the problem described in this work is based on a real factory within the metallurgical sector. This factory and its processes have already been studied in the literature (Muñoz-Díaz et al. 2024; Lorenzo-Espejo et al. 2022). Therefore, this research contributes not only to the existing scientific literature, but also to the decision-making process for production planning in an actual facility.

Starting with the machinery, in the station under consideration there are parallel machines, all of which have to perform the same operation. However, these machines are not identical, and their production speeds are not proportional. In other words, the production speed depends not only on the machine on which a task is performed but also on the nature of the specific task being performed. This distinction is a key factor that distinguishes single-station models with parallel machines. In this scenario, we encounter a problem with Unrelated Parallel Machines (Brucker 2007), where all machines are capable of processing all jobs.

In terms of the objectives of the models, the ultimate goal is always to obtain the assignment of tasks to machines and the sequencing within each machine. However, there are many feasible solutions that fulfil this objective, so it is necessary to establish a criterion for optimisation among all the possible options. This criterion is the objective function of the model and is generally divided into two categories: economic functions and time-based functions (Merchan and Maravelias 2014). In this case, it is a time-based function, specifically minimising the maximum completion time or makespan. In other words, the objective is to minimise the time that elapses between the start of processing the first task and the completion of the last.

At this point, it is important to emphasise that we are not dealing with batches but with individual units. This implies that there is no need to include the batch formation process in either the model or the objective function, contrary to the approach taken by other authors in similar problems (Berber et al. 2007; Méndez and Cerdá 2003). With the criterion for selecting a production schedule now established, we will proceed to explain the most relevant features in the context of the current problem.

The first characteristic to consider is the presence of setups. In production planning models, there are different types of setups: those that depend on the sequence (Liu et al. 2008; Chen et al. 2008), on the machine where the task is to be performed (Sun and Xue 2009; He et al. 2017), on the specific tasks to be processed (Mouret et al. 2011) or on certain resources specific to real plants (Méndez and Cerdá 2002). In this case, we will work with task-dependent setups, specifically based on the sequence of these tasks.

In addition, there will be specific mandatory precedence, i.e. there will be pairs of jobs that must be processed on the same machine and in immediate succession. Finally, there will be no consideration of delivery times for jobs, and it will be assumed that the machines are fully available.

With all this, we have an Unrelated Parallel Machine Scheduling Problem that can be classified according to Graham et al. (1979) as a \(R|prec|C_\mathrm{max}\), where R means that the machines are Unrelated Parallel Machines, prec refers to the fact that compulsory precedence relations are specified, and finally, \(C_\mathrm{max}\) indicates the Objective Function of the problem, minimising the maximum completion time.

3 Mixed integer linear programming models

In this section we present the mathematical formulation of the problem described above. First, for the continuous time representation (subsection 3.1), and second, for the discrete representation (subsection 3.2). Before that, the common parameters, indices and variables for both models are listed below (Table 1).

Table 1 Common parameters, indices and variables in both MILP models
Full size table

3.1 Continuous model

This section presents the Mixed Linear Programming model in its continuous time representation. As mentioned earlier, this formulation splits the time horizon as part of the optimisation process. In this representation, there are different approaches, typically classified as global-event based (Shaik et al. 2006), unit-specific-event based (Floudas and Lin 2004), slot based (Pan et al. 2009), and precedence based (Marchetti and Cerdá 2009b). In this case, we will focus on the last approach, which uses specific variables to represent the start or finish of tasks and binary variables to represent direct precedence relationships between different tasks.

The variables used exclusively for this formulation are presented below (Table 2). This is followed by the MILP model in its continuous formulation and, finally, an explanation of each of the constraints.

$$\begin{aligned} \text {Min} \qquad&C_\mathrm{max} \end{aligned}$$
(1)
$$\begin{aligned} \text {s.a.} \qquad&C_\mathrm{max}\ge C_i{} & {} \forall i=1,2, ...,T \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{j=1}^T y_{0jk}=1{} & {} \forall k \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{k=1}^M \sum _{i\in T \diagdown \{j\} } y_{ijk}=1{} & {} \forall j=1,2, ...,T \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{i \in T \diagdown \{j\}} y_{ijk}=\sum _{l \in T \diagdown \{j\}} y_{jlk}{} & {} \forall j=1,2, ...,T; \forall k \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{k=1}^M y_{ijk}\ge z_{ij}{} & {} \forall i,j=1,2, ..., T \end{aligned}$$
(6)
$$\begin{aligned}&C_j \ge C_i + p_{jk} -E(1-y_{ijk}){} & {} \forall j=1,2,...,T; \forall i; \forall k \end{aligned}$$
(7)
$$\begin{aligned}&C_0 = 0{} & {} \end{aligned}$$
(8)
$$\begin{aligned}&y_{ijk} \in \{0,1\}{} & {} \forall i,j,k \end{aligned}$$
(9)
$$\begin{aligned}&C_i \ge 0{} & {} \forall i \end{aligned}$$
(10)
$$\begin{aligned}&C_\mathrm{max} \ge 0{} & {} \end{aligned}$$
(11)
Table 2 Specific variables of the continuous MILP model
Full size table

The objective function to minimize is stated in Constraint (1) and the Makespan is obtained in Constraints (2). A dummy task is introduced in Constraints (3), which indicate that the dummy task 0 is placed at the beggining of each machine. Constraints (4) ensure that each task has only one immediately previous task, only one immediately subsequent task and is assigned to only one machine, except task 0, the dummy task. Balance equations are included through Constraints (5). Constraints (6) are enforced to guarantee that the mandatory sequences between certain pairs of tasks are fulfilled. Constraints (7) and (8) define the completion time of all tasks. Finally, Constraints (9), (10) and (11) are the basic restrictions on the decision variables.

In assessing the scale of the mathematical model under consideration, the order of magnitude of the number of constraints and variables deserves attention. The number of constraints can be expressed as \(T^2 \cdot M + T^2 + 4 \cdot T \cdot M + 3 \cdot T + 2 \cdot M + 3\), while the number of variables can be given by \(T^2 \cdot M + 2 \cdot T \cdot M + T + M + 2\). This implies a polynomial growth pattern where the number of constraints in the model has a complexity of \(\mathcal {O}(T^2 \cdot M)\) and the number of variables has a complexity of \(\mathcal {O}(T^2 \cdot M)\). Such a characterisation illustrates the increase in constraints and variables concerning the dimensions T and M within the model.

3.2 Discrete model

In this section we present the Mixed Linear Programming model in its discrete time representation. As mentioned earlier, in these models the partitioning of the time horizon is a task that takes place before and outside of the optimisation process. This implies constraints on the times at which each job can start (Burkard and Hatzl 2005), as the points on the horizon where the start of each job can be planned are fixed and no intermediate points can be chosen.

In this case, for this discretisation, a practical upper bound (\(W_\mathrm{max}\)) is used to determine the length of the time horizon. In addition, a time period (U) is used to define the size of each time interval within the horizon, \([U-1, U]\). In this research, U corresponds to a time interval of 30 min.

Next, we present the parameters, index and variables used exclusively for this discrete formulation (Table 3). We then present the MILP model in its discrete formulation, and finally, an explanation of each of the constraints.

$$\begin{aligned} \text {Min} \qquad&C_\mathrm{max} \end{aligned}$$
(12)
$$\begin{aligned} \text {s.a.} \qquad&C_\mathrm{max}\ge C_i{} & {} \forall i \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{k=1}^M \sum _{u\in W_{ik}} y_{iuk}=1{} & {} \forall i \end{aligned}$$
(14)
$$\begin{aligned}&\sum _{i=1}^T \sum _{v=u-p_{ik}+1}^u y_{ivk}\le 1{} & {} \forall k;\forall u \in \{1,...,W_\mathrm{max}\} \end{aligned}$$
(15)
$$\begin{aligned}&y_{(i+1)(u+p_{ik})k} \ge y_{iuk}-E(1-z_{i(i+1)}){} & {} \forall i \in \{1,...,T-1\}, \forall k, \forall u; \end{aligned}$$
(16)
$$\begin{aligned}&C_i = \left[ \sum _{k=1}^M \sum _{u\in W_{ik}} y_{iuk}.(u+p_{ik}) \right] -1{} & {} \forall i \end{aligned}$$
(17)
$$\begin{aligned}&y_{ijk} \in \{0,1\}{} & {} \forall i,j,k \end{aligned}$$
(18)
$$\begin{aligned}&C_i \ge 0{} & {} \forall i \end{aligned}$$
(19)
$$\begin{aligned}&C_\mathrm{max} \ge 0{} & {} \end{aligned}$$
(20)
Table 3 Specific parameters, index and variables of the discrete MILP model
Full size table

The objective function to minimize is stated in Constraint (12) and the Makespan is obtained in Constraints (13). Constraints (14) require each task to be started exactly once and Constraints (15) ensure that at a given time period u, only one task can be executed on each machine. Constraints (16) are enforced to guarantee that the mandatory sequences between certain pairs of tasks are fulfilled. Constraints (17) define the completion time of all tasks and Constraints (18), (19) and (20) are the basic restrictions on the decision variables.

When assessing the scale of the mathematical model under consideration, the order of magnitude of the number of constraints and variables needs to be examined. The number of constraints is expressed as \(T \cdot M \cdot W_\mathrm{max} + T^2 \cdot M + 4 \cdot T + 1\), while the number of variables is given by \(T \cdot M \cdot W_\mathrm{max} + T + 1\). This implies a polynomial growth pattern, where the number of constraints has a complexity of \(\mathcal {O}(T \cdot M \cdot W_\mathrm{max})\), since \(W_\mathrm{max}\) is necessarily greater than T, and the number of variables has a complexity of \(\mathcal {O}(T \cdot M \cdot W_\mathrm{max})\). Such a characterisation illustrates the increasing constraints and variables concerning the dimensions T, M and \(W_\mathrm{max}\) within this model.

4 Results and conclusions

As mentioned above, the problem described is based on a real production planning problem in a metallurgical plant. This has allowed the use of time estimations derived from the actual historical data of the factory. In addition to the time estimations, the priority relationships are also based on a real project, and the different configurations represent situations of interest to this industry.

These configurations are characterised by the number of machines available for task processing, shown in the column M, and the number of tasks to be scheduled, shown in the column T. Configurations with 2, 4 and 6 machines were chosen, and for each of these 20, 40, 80 and 160 tasks were considered, giving a total of 12 configurations. All were run for both models, with the same processing times for each task and the same priority relationships for each configuration.

A time limit of 2 h was also implemented as a time constraint for model execution. When this limit was reached, the model stopped and returned the best solution achieved up to that point, together with the corresponding makespan. In cases where this measure was implemented, the column Runtime in Table 4 contains the abbreviation LR (limit reached). In order to facilitate the interpretation of the results, for each of the twelve configurations, the best result in terms of makespan, i.e. the lowest maximum completion time between both models, has been highlighted in bold.

Both models have been implemented in Python and solved on an Intel® Core™ i7-4790 CPU at 3.60 GHz with 12 GB of RAM using Gurobi Optimizer v9.1.1.

Table 4 Comparison of Makespans (hours) and runtimes (seconds) obtained for the 12 configurations in the continuous and discrete models. LR: limit reached (2 h/7200 s)
Full size table

These results are analysed in more detail in the following, with the aim of responding to as wide a range of situations as possible.

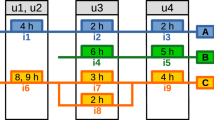
Strictly considering the makespan, which is the only objective in both objective functions (Constraints 1 and 12), it is evident that the continuous model gives better results in all cases. In fact, the results show that the makespan of the discrete model is higher than that of the continuous model, ranging from 3.2% (M = 4, T = 20 and M = 6, T = 40) to 18% (M = 2, T = 160). This result is consistent with the implications of the time discretisation itself, because even if both models were to choose exactly the same scheduling, it is highly likely that the discrete model would result in a higher makespan. This is due to the losses incurred in assigning tasks with real processing times, which may not be multiples of U, to time intervals of duration U. In most cases, this will result in idle times in the last interval in which each task is assigned in the discrete model. To illustrate this concept, consider a simple example with only two tasks, A1 and A2. Assuming that the time discretization for the discrete model is one hour (U = 1 h), if tasks A1 and A2 have durations of 3.2 h and 4 h respectively, the discrete model would give a makespan of 8 h compared to the continuous model’s 7.2 h (Fig. 1), despite returning the same actual schedule.

Fig. 1
figure 1

Gantt chart of the continuous and discrete models for two identical tasks (A1 and A2) following the same sequence

Full size image

This phenomenon occurs to a minor extent if the size of the individual time intervals (U) is reduced, because the unallocated times generated will have a shorter maximum duration. However, using smaller U intervals will also result in longer execution times. Furthermore, these unallocated times will always be present, and with a greater number of tasks, the probability of generating unallocated times increases. This can be clearly seen in the results: as the number of tasks increases, the difference between the makespans of the continuous and discrete models increases significantly (Table 4).

In order to better study the influence of the number of tasks and machines on the difference between the results of the two models, Table 5 is presented. In this table, the first two columns again give the number of machines (M) and the number of tasks (T) for each configuration run. The third column (Makespan difference) shows the difference between the makespans, with the continuous model consistently giving smaller makespans. The fourth column (Runtime difference) shows the difference between the runtimes obtained, where LR indicates when one of the models reached the time limit. Finally, the fifth column (Best Runtime Performance Model) indicates which model delivered the better runtime performance. In this last column, a dash (-) appears when both models reached the time limit. In cases where only one model reached the time limit, LR is displayed in the Runtime Difference column, and the Best Runtime Performance Model column indicates the model that did not reach the time limit and therefore provided the best runtime.

Table 5 Difference between the performance of the two models in terms of makespan and execution times
Full size table

With these results in mind, it is easy to see that the difference between the makespans of the two models does indeed grow as the number of tasks increases. Furthermore, when we increase the number of available machines, this growth is significantly mitigated. This confirms that the problem of time discretization becomes more pronounced as more tasks are assigned to the same machine, leading to an accumulation of unallocated times.

It is important to note that the solution returned by the discrete model does not have a higher makespan solely due to unallocated times. Additionally, the assignment and sequencing of tasks does not always coincide with that of the continuous model. Therefore, if the term net makespan refers to the makespan resulting from removing unallocated times from the schedule returned by the discrete model, the net makespan of the discrete model is equal to or higher than that of the continuous model in all configurations studied. This is also due to the loss of accuracy caused by the discretisation of time.

Finally, regarding the makespan, it’s worth noting that the continuous model reaches the time limit for the first and only time with 6 machines and 160 tasks. However, its makespan is still lower than that of the discrete model, which does not reach the time limit. This again emphasises the loss of efficiency in the discrete model due to the inherent discretisation of the time horizon.

On the other hand, if we now turn our attention to the execution times, the continuous model again delivers better results than the discrete model in all but one configuration. Furthermore, if we look at the runtimes in Table 4, we can see that the model does not take more than half a minute in any of the configurations with 20, 40 and 60 tasks. However, when the number of tasks increases to 160, the time limit of 2 h is reached in all cases. On the other hand, the discrete model reaches the time limit in problems with fewer machines and does not do so as the number of machines increases.

In conclusion, for environments with these characteristics, the use of continuous models is clearly more advantageous, as they provide solutions with better makespans and runtimes. However, an interesting line of future research would be to extend both mathematical models to other industries where the number of tasks is higher, as the performance of the discrete model suggests that it could give better results in such environments compared to the continuous model.