1 State of the art

The behavior of rolling bearings during operation depends on their raceway geometries [1]. The design of rolling bearing arrangements is usually based on the assumption of geometrically ideal raceways, which consequently requires tight tolerances for both bearing components and bearing seats. For rolling bearings, several international tolerance-defining standards exist. For example, geometrical product specifications (GPS) and tolerances for radial bearings can be found in ISO 492 [2] while ISO 12297‑1 [3] defines boundary dimensions, GPS, tolerances and gauges of cylindrical steel rollers used in roller bearings. In addition, limits for radial internal clearance classes of rolling bearings are specified in ISO 5753‑1 [4].

In contrast, there is currently no normative standard for geometrical tolerancing of the bearing ring seats of shafts and casings, which are typically in-house produced parts. A related German norm (DIN 5425‑1 [5]) was withdrawn in 2010, while the American standard ANSI/ABMA 7 [6] proposes shaft and housing fits selected from the ISO fit system [7], but no specifications of geometrical tolerances like cylindricity or concentricity of the seats. Furthermore, various recommendations for dimensional and geometrical tolerancing of the bearing seats exist on the part of rolling bearing manufacturers (cf. e.g. [8,9,10,11]), which include tight ISO tolerance grades down to IT4/2.

Compliance with these narrow limits requires costly precision manufacturing [12]. On the other hand, exceeding these specifications may potentially have undesirable effects on the operating behavior of the bearing, for example when form or runout deviations of the bearing seats are transferred to the raceways due to mechanical deformation. Wavy raceway surfaces can strongly affect the dynamic behavior of rolling bearings, where they may cause increased friction or vibrations [13] as well as acoustic effects such as whistling [14]. Various techniques for modeling these effects have been developed, ranging from analytical spring-mass approaches [15] to numerical methods which allow for integration of multiaxial load states [16] as well as centrifugal forces and gyroscopic moments [17].

In addition to possible impacts on the dynamic behavior, it has also been shown that production- or assembly-related geometrical deviations affect bearing fatigue life due to changes in the internal load distribution. Many investigations in this context focus on variations of internal bearing clearance caused by inevitable diameter variations of raceways—which may also result from ring deformations due to press fits—and rolling elements. Multiple examples can be found for deep groove ball bearings [18,19,20,21], angular contact ball bearings [22] and cylindrical roller bearings [19, 23, 24]. These analyses show that bearing life can be increased by adjusting the amount of clearance or pretension to the respective operating conditions.

Apart from changes of clearance, another mode of deformation that has been examined (e.g. in [25,26,27]) is an ovalization of the outer bearing raceway, which is frequently observed in thin-walled planetary gears due to load-induced deformation. In this case, the acting interlocking forces cause the gear to deform elliptically such that the major axis is aligned parallel to the external bearing load, which leads to a relief of the most heavily loaded rolling element. An ovalization of the right magnitude—which depends on the respective boundary conditions—may thus contribute to a more uniform load distribution within the bearing and hence longer fatigue life [25].

However, calculation of raceway deformations in the aforementioned examinations is based either on analytical formulas, which are available only for simple problems like circumferential contact of geometrically ideal rings [28] and (curved) beam-like structures with known loads [29]—as in the case of thin-walled planet gears—or on time consuming finite element analysis (FEA). Consequently, they are not suitable for statistical tolerance analyses with non-ideal part geometries, which are essential in order to determine the distributions of functional key characteristics—such as fatigue life—resulting from real manufacturing processes so as to be able to statistically assess fulfillment of requirements.

To this end, previous investigations have been conducted in [30] and [31] on radially loaded cylindrical roller bearings. In [30], the influence of diameter variations of bearing components and bearing seats and radial form deviations of the bearing seats on clearance, fatigue life and vibrational behavior was examined using a 2D cross section bearing model. After creating 10,000 samples of deviated bearings and seats using a Monte Carlo approach, the assembly process was simulated employing the formula for geometrically ideal rings (cf. e.g. [28]) with an FE-based correction factor. In the following, mean bearing clearance was evaluated by a ray-tracing algorithm and the determined mean clearance value was then used to calculate fatigue life. As a consequence, the effects of form deviations could not be clearly identified since the consideration of the internal bearing geometry through a mean clearance effectively reduced the analysis to a diameter variation of the bearing rings. It was observed that bearing fatigue life increased as mean clearance diminished, whereby no negative clearance values (“preloading”) occurred. Vibration behavior was also investigated for some samples on the edges and in the center of the design space. For low frequency form deviations considered in this case, vibrations primarily occurred orthogonal to the load direction.

In [31], all deviations were directly applied to the bearing raceways and rollers, neglecting the bearing seats. A superposition of 50 harmonic radial form deviations (beginning at a spatial frequency of 2 circumferential undulations, i.e. an ovalization) was considered for each component in addition to variations of raceway and roller diameters. 36,000 Monte Carlo-sampled bearings were evaluated with regard to total inner ring displacement, clearance and deflection. Due to the high number of form deviations—resulting in small individual amplitudes—and the binning of the different waviness frequencies in the sensitivity analysis, no significant effect of form deviations was observed. Thus, depending on the respective result quantity, diameter deviations of raceways and loaded or diametrically opposite rollers as well as roller profiles had the greatest impact. While the statistical distributions of individual roller loads were determined, fatigue life was not evaluated.

In summary, a number of previous works on the influence of different geometrical deviations on the functional properties of rolling bearings exist, yet none of them are capable of considering arbitrary, statistically distributed geometrical deviations of bearings and seats since they either neglect part deformations altogether or depend on simplifying analytical approaches (e.g. limitation to diameter variations) or time-consuming FE simulations for their computation. This paper therefore introduces a method to bridge the current gap and enable statistical analyses of the operating behavior of cylindrical rolling bearings taking into account actual shapes of the connecting components and bearings.

2 Method for integration of geometrical deviations in the design of cylindrical rolling bearing arrangements

The method presented herein is based on a combination of three-dimensional statistical tolerance analysis and multi-body simulation. For the statistical simulation, a large number of individual cases (“samples”) are evaluated in order to determine the distribution of key characteristics such as bearing fatigue life resulting from the distributions of the dimensional, shape and position deviations of the components. The sample-dependent values of the deviations may be obtained either from a systematic Design of Experiments (DoE) based scheme such as Latin Hypercube Sampling (LHS) so as to screen the parameter space or by drawing from arbitrary statistical distributions (e.g. normal distributions) to simulate manufacturing processes (Monte Carlo sampling). For individual cases (e.g. on the edges of the design space), multi-body simulations may be utilized to investigate the dynamic operating behavior, especially with regard to unwanted vibration excitations. Based on the results, tolerances can then be adjusted if necessary to ensure fulfillment of the specified requirements such as in terms of minimum bearing life and smooth running.

An illustrative overview of the procedure of the method is given in Fig. 1. In a first step, the general simulation settings, system components (i.e. bearings and the corresponding inner and outer ring seats in the casing and on the shafts), deviations and operational parameters like acting loads are defined in a custom XML input file (Fig. 1, top left). The geometrical deviations are modeled using a two-dimensional inverse Discrete Fourier Transform (DFT), which is capable of representing arbitrary deviations through superposition of harmonic waves and is implemented by default in many programming languages by means of efficient Fast Fourier Transform (FFT) algorithms. However, the method presented herein also allows for alternative modeling approaches such as Fourier-Legendre polynomials [32]. From a mathematical point of view, any complete basis of the vector space spanned by the set of nodal displacements can be utilized to generate any kind of deviation.

Fig. 1
figure 1

Procedure of the presented method for the integration of geometrical deviations in the design of cylindrical roller bearing arrangements

Full size image

A mathematical formulation of the 2D inverse DFT for a real-valued discretized function f, which in this case means an \(M\times N\) matrix of radial surface point displacements, is given in Eq. 1. Therein, m and n are the matrix (surface point) indices, fm,n are the related function (displacement) values and u and v are the spatial frequencies along the two dimensions of the matrix (i.e. surface). The coefficients A and P represent amplitudes and phase angles of the individual harmonic waves whose superposition yields the function values. Their indices describe the propagation direction of the corresponding undulation. For example, A4,3 is the amplitude of a wave with 4 periods along the first (axial) and 3 periods in the orthogonal (circumferential) direction.

$$\begin{aligned}f_{m,n}&=\frac{1}{M\cdot N}\cdot {\sum }_{u=0}^{\left\lfloor \frac{\left(M-1\right)}{2}\right\rfloor }{\sum }_{w=0}^{\left\lfloor \frac{\left(N-1\right)}{2}\right\rfloor }\left[A_{u,w}\cdot\right.\\ &\mathit{\sin }\left(2\pi \cdot \left(m\cdot \frac{u}{M}+n\cdot \frac{w}{N}\right)+P_{u,w}\right)+\\ &\left.A_{-u,w}\cdot \mathit{\sin }\left(2\pi \cdot \left(m\cdot \frac{-u}{M}+n\cdot \frac{w}{N}\right)+P_{-u,w}\right)\right]\end{aligned}$$
(1)

While the DFT is principally capable of representing arbitrary radial deviations since it provides a complete basis of the vector space [33], specific relevant deviation types such as conicity and crowning of the cylindrical surfaces can be described more easily through a separate implementation. In addition, radial offset of the seat halves as occurring in split casings as well as position deviations and tilts of the bores in the housing are also modeled separately since they are not covered by the DFT.

The tolerance analysis settings defined in the XML input file are then processed by a matlab program (Fig. 1, bottom left), which generates the deviated geometries of the bearings and the corresponding inner and outer ring seats for the individual samples based thereon. In order to achieve statistically stable results, 10,000 samples are created. Thereafter, the interference-induced deformations of the bearing raceways are computed for every sample. For geometrically ideal circular rings, an analytical solution exists which can also be applied to rolling bearings [28]. However, this does not hold true if the parts deviate from their nominal shapes. The proposed method therefore includes a metamodeling approach based on interpolation between FEA reference results, which enables consideration of form defects.

This approach employs the amplitudes Ai of the considered deviations, the phase angle differences ΔPi between them and the difference D between the mean radii of the bearing ring and the bearing seat surface as input parameters (i.e. independent variables). In a first step, a user-specified number of FEA models are automatically created and solved following a full factorial Design of Experiments (DoE) table of input parameter values. The radial node displacements Uref of the raceway surfaces are then extracted. After creation of these reference points, the raceway deformations of the individual samples are computed by interpolating between the FEA solutions of the neighboring reference points based on the values of the input parameters. The approach is visualized in Fig. 2 for an inner ring seat. In this example, a harmonic waviness of the seat surface with six periods along the circumferential direction as well as a diameter variation of the bearing ring are considered. Consequently, there are two input parameters (A and D), which requires a bilinear interpolation. For each sample, the weighting factors w of the four adjacent FEA reference points equal the area of their opposing rectangle divided by the summed area of all four rectangles.

Fig. 2
figure 2

Interpolation of sample raceway deformations between FEA reference solutions (shape deviations exaggerated for visualization purposes)

Full size image

After computation of the raceway deformations, operational clearance is evaluated for each sample utilizing a ray-tracing algorithm as described in [30]. The raceway geometries of all samples are then transferred to a transmission design software capable of accounting for raceway deformations during computation of the mechanical system loads (in this case, FVA Workbench) together with the relevant operational parameters (external loads, temperatures etc.) via a spreadsheet file (Fig. 1, top center). In FVA Workbench, the modified reference rating lives (L10mrh) of the bearings are calculated according to ISO/TS 16281 [34] for each sample. It is worth mentioning that while the algorithm described in ISO/TS 16281 is generally capable of dealing with arbitrary raceway geometries, FVA Workbench is limited to additive superpositions of axial and circumferential shape deviations as of release 8.1. The results are again exported to a spreadsheet and subsequentially analyzed in matlab (Fig. 1, right), where statistical and graphical evaluations as well as sensitivity analyses can be carried out (cf. Sect. 3). Based on the results, additional tolerance analyses with adjusted tolerances can be conducted if life requirements are not met. Furthermore, the dynamic bearing behavior may be analyzed through multi-body simulation (MBS) for critical cases (e.g. maximum raceway deformations) to ensure smooth operation even under worst-case conditions.

3 Statistical tolerance analysis

The developed method is illustrated by the example of the belt diverter unit shown in Fig. 3 comprising two cylindrical roller bearings of type NU216 (B I, loose bearing) and NUP216 (B II, fixed bearing). The shaft (material E295) transmits 150 kW at 2,000 rpm. The sum of belt forces F acting on each pulley is 9.5 kN, effecting a load PB of 21 kN on both bearings, which are grease-lubricated (ISO viscosity grade 100) and operate at a temperature of 50 °C. The casing with an outer diameter (DA) of 164 mm is made of S235JR. The axial distance between the bearing center points (l) is 160 mm.

Fig. 3
figure 3

Exemplary belt diverter unit and considered seat form deviations

Full size image

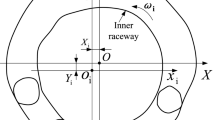
In the example analyzed herein, an axial waviness with three periods on the shaft seat and a circumferential waviness with 18 periods on the casing seat are considered at the left bearing position (I), while a circumferential waviness with three periods on both seats is taken into account at the right bearing position (II) utilizing the DFT (see Fig. 3). These form errors are exemplarily chosen in order to examine the effect of the spatial frequency as well as the propagation direction of geometrical form errors of the seats on their transfer to the raceways. The origins of the waves are marked with an X. They propagate along the u axis (axial) and according to the right-hand rule about u (circumferential). Furthermore, a positioning error of the casing bores, given in polar coordinates (radial offset Δr, polar angle φ), is included. With regard to the bearings, which are usually bought parts, dimensional variations of the bore (d) and outer (D) diameter within the limits of tolerance class “Normal” according to ISO 492 [2] are considered (i.e. [−15;0] µm for the bore and [−18;0] µm for the outer diameter). In addition, the initial bearing clearance is assumed to be within the limits of clearance class N ([40;75] µm) as defined in ISO 5753‑1 [4], which is achieved through symmetrical variation of the inner and outer raceway diameter. For both bearings, the parameter values specified in Table 1 are assumed. The bearing seats are toleranced according to the scheme proposed in [8], which employs specifications of the total circular (t1) and planar (t2) runout of the bearing seats (cf. Fig. 4).

Table 1 Parameters for bearing types NU216 and NUP216
Full size table
Fig. 4
figure 4

Bearing seat tolerancing scheme according to [8]

Full size image

Two analyses are conducted: In the first investigation, standard tolerance values as recommended in [8] are applied. For comparison, a second analysis is carried out where tolerances are extended by two ISO tolerance grades. Additionally, the fundamental deviation of the casing bore is changed from H to JS to limit the maximum clearance between outer ring and bore. Table 2 shows an overview of the applied seat tolerances.

Table 2 Tolerance values used in the statistical analyses
Full size table

Considering Fig. 5, the following relations between radial offset Δr, total circular runout error ΔR and total planar runout deviation ΔP of the casing bores can be established:

$$\alpha =\tan ^{-1}\left(\frac{2\cdot \Updelta r}{l}\right)$$
(2)
$$\Updelta R=\left(B-D\cdot \tan \left(\alpha \right)\right)\cdot \sin \left(\alpha \right)$$
(3)
$$\Updelta P=D\cdot \sin \left(\alpha \right)-\Updelta R\cdot \tan \left(\alpha \right)$$
(4)
Fig. 5
figure 5

Planar (ΔP) and circular (ΔR) runout errors resulting from radial casing bore position offset Δr (exaggerated)

Full size image

The total permissible deviations defined by the tolerance limits for catalog and extended tolerances are split between the individual considered parameters as follows: By deriving Eqs. 3 and 4, it can be readily established that in this example, ΔP increases faster than ΔR with Δr or α. Consequently, the maximum permissible value of the radial position offset Δr is determined by the total planar runout tolerance t2, which equals ΔP. The remaining circular runout tolerance after subtracting the error ΔR due to Δr from t1 is then equated to the maximum acceptable peak-to-valley height (i.e. two times the amplitude) of the waviness. The remaining fit tolerance of the seat, which is obtained by shifting both fit limits inward (towards the mean) by two times the maximum waviness amplitude, is assigned to a uniform diameter variation. The shaft seat deviations are determined using the same algorithm, however no planar runout error is considered here.

The individual samples are then generated through a Monte-Carlo process, i.e. by drawing the parameter values from random distributions. In this case, normal distributions which are characterized by their mean (\(\mu\)) and their standard deviation (σ) are assumed in order to model a real manufacturing process [35]. With regard to the bearing seats, all parameters—except for the Fourier phase angles and the casing bore polar angles φ, which are drawn from uniform distributions—are sampled from normal distributions whose mean \(\mu\) is centered within the range T of permissible values with a standard deviation of T/8, which corresponds to process capability indices Cp and Cpk of 1.33 (cf. ISO 22514‑2 [36]). The same distribution parameters are also adopted for the initial bearing clearance. For the bore (d) and outer diameter (D) of the bearing on the other hand, the manufacturing process is assumed to be tuned in such a way that the mean is located at a distance of T/3 from the maximum material size (MMS) and this distance measures four standard deviations (Cp = 2, Cpk = 1.33).

For each of the four bearing ring seats, a grid of FEA reference solutions with 24 supporting points is computed as a foundation of the meta-model from which the individual raceway deformation is then interpolated for each sample. The histograms of the modified reference rating lives (L10mrh) of both bearings obtained from the two analyses with catalog-based (top) and extended (bottom) tolerances can be seen in Fig. 6.

Fig. 6
figure 6

Life histograms with catalog (top) and extended (bottom) tolerances for bearing I (left; considered form errors: Axial waviness with 3 periods on shaft seat and circumferential waviness with 18 periods on casing seat) and II (right; considered form errors: Circumferential waviness with 3 periods on shaft seat and 3 periods on casing seat)

Full size image

The resulting bearing life of every sample has been calculated from a total of four individual values corresponding to two rotational positions of inner ring and roller set respectively. As expected, the standard deviations (scattering) of bearing lives are considerably smaller and the means values of both bearings are closer to each other with catalog tolerances as compared to the results with extended tolerance values. In this example, an increase of mean modified reference bearing life with extension of tolerances is observed for both bearings. In the case of bearing I, a rise of 30% (from 60,771 to 78,991 h) occurs. The lower bound of the value range also increases from 44,687 to 53,637 h, which means the rate of premature failures—whose value depends on the required minimum fatigue life—declines. With bearing II on the other hand, the mean also increases by 12%, but minimum bearing life drops from 46,287 to 33,313 h and therefore an elevated rate of untimely bearing failures must be expected.

In summary, it can be stated that while the bearing seats on both sides are identically toleranced, the resulting distributions of bearing lives differ due to the different kinds of form errors present. While the difference is small if tight tolerances according to current bearing manufacturer catalogs are applied, it increases when tolerances are widened. However, depending on the type of the occurring form errors, the observed changes with extended tolerances are not necessarily negative. Therefore, no straightforward relation between tolerance width and bearing life can be established and a case-specific analysis is advisable. In this context, it is worth noting that the possible ramifications of tolerancing on the assembly process due to interference fits should also be taken into account in the tolerance allocation process.

For a detailed examination of the influence of the individual deviation parameters on bearing life, a sensitivity analysis for the case of extended tolerances is conducted utilizing the “moment independent uncertainty indicator” δ proposed by Borgonovo [37] employing the algorithmic implementation from [38]. This dimensionless indicator takes values between zero and one with zero meaning that the distribution of an input quantity has no effect on the analyzed result quantity and one meaning that the variation of the result quantity is entirely caused by the variability of the input quantity.

Table 3 shows the results of the sensitivity analysis for the modified reference rating life of both bearings. Only those input parameters with an indicator value of δ ≥ 0.05 are listed. It can be seen that initial (pre-assembly) internal bearing clearance greatly influences bearing life, as does the casing seat diameter. Due to the tighter tolerance limits, the influence of the diameter variation of the shaft seats is less pronounced (for seat II, it is below 0.05). The bearing fit diameters (d, D) are not relevant here since their spread is small. Variations of the bearing fit or seat diameters lead to a constriction or widening of the raceway diameters during assembly and thus have the same principal effect on clearance and life as changes of the initial clearance.

Table 3 Sensitivity analysis results (Borgonovo Delta) for bearing lives with extended tolerances
Full size table

With regard to shaft seat waviness, an effect of the amplitude is observed for both seats, whereas the phase angles are of no importance. In the case of the axial waviness on seat I, this is due to the fact that its effect on the inner raceway is limited to a uniform widening of its diameter because the axial stiffness of the bearing ring prevents a transfer of the undulation (in the FEA simulations, the maximum peak-to-valley raceway height difference is 1.8 µm compared to 15 µm at seat II). Considering the circumferential waviness of seat II, the bearing is always subjected to the entire range of phase angles because of the shaft rotation and the sampled value is thus not relevant.

Concerning the casing seats, no significant effect of the waviness is observed for seat I. Similar to the shaft seat, virtually no transfer of the waviness to the raceway occurs due to the short wavelength (2 µm maximum raceway height difference in FEA compared to 17 µm at seat II) and its effect is limited to a diameter constriction, whose effect is below 0.05. With seat II on the other hand, both the waviness amplitude and particularly the phase angle notably influence bearing life. The positioning errors of the casing bores have no significant effect in this case since their distributions are centered around the nominal positions. Even in cases where both bore centers exhibit their maximum permissible radial offsets—which implies two simultaneous four-sigma events—in diametrically opposing directions, the resulting shaft misalignment is less than 2′.

For further analysis, a parallel coordinate diagram of the contributors in Table 3 to the fatigue life of bearing II is shown in Fig. 7. With regard to clearance and casing seat diameter, low values are advantageous since a small clearance or slight preload positively affects the internal load distribution and therefore causes bearing life to increase (cf. e.g. [30]). To this end, the switch from a clearance to a transition fit (H to JS) on the casing seat has a beneficial effect. While the waviness amplitude of the shaft seat contributes to a reduction of clearance, it also causes higher peak roller loads during shaft rotation which are detrimental to bearing life. Consequently, the maximum life values mostly occur with amplitudes in the lower half of the spectrum. On the stationary casing seat, a different constellation is observed: The waviness amplitudes are similar for maximum and minimum lives, but a clear separation in terms of the phase angles can be determined. While the best performing samples are linked to values around 90°, the minimum lives are found around 270°. The explanation for this effect can be seen in Fig. 7 on the right: A phase angle of 90° corresponds to a maximum of the outer bearing seat waviness at the position of the most heavily loaded roller, which in turn causes a lowering of the raceway in this area. As a consequence, the peak roller load is reduced and the load arc (Q) is widened. Thus, the total load (P) is more equally distributed among the rollers and bearing life increases. This illustrates that the effect of geometrical imperfections of seats or raceways on bearing life is not necessarily adverse in all cases. With a phase angle of 270° on the other hand, a contrary effect occurs, i.e. an increase of maximum roller load due to an elevation of the raceway in the load zone. As a result, bearing life declines. The lower minimal life values with extended tolerances observed with bearing II as compared to bearing I are due to the fact that the form errors of the seats (cf. Fig. 3) are transferred to the raceways to a large extent due to their low spatial frequency and cause an increase of maximum roller loads in adverse constellations (cf. Fig. 7).

Fig. 7
figure 7

Parallel coordinate plot of contributors to modified reference rating life of bearing II (left), influence of casing waviness phase angle on bearing load distribution (right, schematic representation)

Full size image

In the case of bearing I on the other hand, the transfer of the shape deviations from the seats to the raceways is greatly reduced due to their short wavelengths and a uniform change of the raceway diameters—which leads to a reduction of internal clearance—becomes the dominant effect instead. Since the occurring beneficial reduction of clearance is more pronounced with extended tolerances for the majority of the samples, the increase of mean bearing life by approximately 30% compared to catalog tolerances can be accounted for.

While the positive effect of reduced bearing clearance values or even a light preloading (“negative clearance”) on fatigue life has been reported many times in the literature, clearance adjustments through modifications of the seat fits and tolerances are associated with some caveats. First of all, attention should be paid to the fact that form errors occurring within the allowed limits may reduce or overturn the desired effect (cf. Fig. 7, bottom right). Secondly, the assembly effort may increase if a transition fit is chosen instead of a clearance fit in order to achieve a diameter constriction of the bearing ring during assembly. Thirdly, press fits inevitably give rise to hoop stresses within the bearing rings. While this fact is acknowledged in ISO 281 [39] upon which ISO/TS 16281 [34] is based, no quantitative statements regarding their influence on fatigue life are included therein. On the other hand, it is known that compressive hoop stresses as occurring in interference-fitted outer rings cause an increase of fatigue life, while the tensile stresses present within press-fitted inner rings have the opposite effect (cf. e.g. [40]). Thus, if a tight inner ring fit is chosen to achieve a clearance reduction, the desired effected may be diminished or inverted by the increased hoop stress level. In any case, bearing clearance must be chosen such that no thermal runaway of the bearing (i.e. a positive feedback loop between thermal expansions and frictional torque due to preloading) can occur.

4 Influence of geometrical deviations in raceway contacts on dynamic bearing behavior

In multi-body simulations with circumferential wave-shaped form errors of the raceways, two different kinds of roller movements, that is to say the phase-synchronous and the phase-asynchronous type, can be observed. These can be distinguished based on the ratio of the total number of oscillations (fAR) to the number of rollers (iWK). Phase-synchronous movements occur for integer values of this ratio, where the rollers move synchronically through the peaks and valleys of the raceway during rotation of the roller set. The value of the ratio corresponds to the order of excitation (first, second etc.). For non-integer ratios on the other hand, the roller movement is asynchronous. These effects are visualized in Fig. 8. Therein, the results of three multi-body simulations of a cylindrical roller bearing of type NU216 with 18 rollers with an increasing number of periodic outer raceway oscillations are depicted. In the central plot (b), an increased excitation of the first order is observed because the ratio of fAR to iWK is 1 and therefore a phase-synchronous movement occurs. The acceleration obtained through a Fast Fourier Transform is 125.5 mm/s2. In contrast, the roller movements in plots (a) and (c) are phase-asynchronous. Consequently, no significant excitation is observed in these cases.

Fig. 8
figure 8

Influence of the number of undulations fAR on excitation of vibrations observed during multi-body simulation at a constant peak-to-valley distance aAR of 21 µm (\(C_{0}/P\)= 8, \(n_{IR}\)= 2,000 min−1)

Full size image

Since manufacturing-related shape deviations of the rings usually have a waviness of \(f_{AR}=2\) to \(f_{AR}=6\), i.e. an ovalization or the shape of an orbiform, the case shown in plot (b) does not typically result from the manufacturing process. Such a deformation pattern can for example be caused by extreme impacts on the bearing if the load gets so high that the rolling elements plastically deform the raceway. The number of indentations then corresponds to the number of rolling elements. Due to the load arc develo** within radial bearings (cf. Fig. 7, right), the depth of the resulting indentations typically depends on their position along the circumference, with the largest deformation occurring at the location of the highest loaded roller. Constant indentation depths are usually observed in bearings whose raceways support axial forces, e.g. angular contact ball bearings, tapered roller bearings or axial bearings.

5 Summary and outline

Within this contribution, a novel method for the integration of statistically distributed geometrical part deviations in the design of cylindrical roller bearing arrangements has been laid out, which is based on a combination of statistical tolerance analysis and multi-body simulations.

By application in an exemplary use case, it could be shown that the influence of geometrical imperfections on operational behavior greatly depends on the types of the present deviations and no general relation between specified tolerance ranges and key characteristics such as bearing fatigue life or vibration behavior can be established. It is therefore advisable to consider the individual boundary constraints in the design stage in order to ensure fulfillment of the functional requirements and reduce manufacturing costs by avoiding unnecessarily tight tolerances. Furthermore, by adjusting tolerances to the respective application instead of relying on standard catalog recommendations, an increase of bearing life may be achieved, although it should be mentioned that this requires knowledge of the types of geometrical deviations occurring in the application at hand since different deviations lying within the same tolerance limits may have contrary effects, as has been shown in this article. Additionally, this may come at the cost of a more elaborate manufacturing and/or assembly process (e.g. when a clearance fit is changed into a transition fit). In order to identify and avert possible unwanted tolerancing-related dynamic effects such as bearing vibrations, multi-body simulations should be conducted for individual critical cases, e.g. maximum raceway deformations.

Future work is aimed at extending the method to other bearing types, which can be achieved by implementing additional geometry models. Moreover, examinations of the effects of fit surface deviations on ring creep, which may cause premature bearing failure, are to be conducted. In perspective, the method described herein is to be fully integrated into the design process of transmissions by enabling sampling of geometries based on geometrical product specification (GPS) and establishing suitable user and program interfaces, thus allowing design engineers to carry out an automated statistical evaluation of the effects of deviated bearing and seat geometries on system performance. Once a fully automated data exchange has been achieved, the method may also be adapted for tolerance optimization, for example to ensure fulfillment of a required minimum service life at the lowest possible manufacturing costs.