1 Introduction

The Winkler–Pasternak-type elastic foundation has been widely adopted by many researchers as a suitable model in various practical applications. Accurate determination of the soil–foundation behavior is of great importance for the safety of the structure. Elastic foundations have many engineering applications, especially in soil mechanics, ice engineering, highway pavement, strip foundations, etc. [1].

Since soil–foundation interaction is very complex, many models have been developed to represent soil–foundation behavior. The first and simplest elastic soil model is the Winkler model [2], which assumes that the soil consists of discrete springs. Some mechanical soil models have been proposed to predict the interaction between the foundation and the structure. The simplest foundation model developed by Winkler is called single parametric model and assumes that the foundation consists of discrete springs. Since the Winkler model fails to provide continuity due to the discrete spring assumption, other different models have been proposed, the most famous of which is the two-parameter Winkler–Pasternak model. A Winkler–Pasternak model, a more advanced model than the Winkler model, proposed a shear stiffness coefficient to describe the foundation and added a shear layer to the Winkler model. Due to its importance, many researchers have conducted studies involving the Winkler model or the Winkler–Pasternak model. Huang et al. [3] investigated the elasticity solution of FG thick plates resting on Winkler–Pasternak foundation using the state space method. Atmane and Tounsi [4] investigated a new high shear deformation theory for free vibration analysis of a functionally graded (FG) plate supported on a Winkler–Pasternak foundation. The material properties of the FG plate are assumed to obey the exponential function or power law function. Nobili [5] presented the nonlinear stress-free free boundary problem for beams resting on a Winkler or Pasternak elastic foundation. Free vibration analysis of uniform beams resting on Pasternak foundation was investigated by Le et al. Bending and torsion modes are analyzed, and it is found that the effect of rotational inertia reduces the natural frequencies. Avcar and Mohammed [6] investigated the free vibration of FG beams supported by Pasternak foundation. Stephen and Ch’ng [7] investigated the diverging contact problem of an Euler–Bernoulli beam resting on a Winkler foundation.

Contact problems have an important place in soil mechanics. There are not many studies on the contact problem of a layer supported by a Winkler elastic foundation. Marzeda et al. [8] investigated the contact mechanics of a homogeneous wedge supported by a Winkler foundation. The problem was reduced to an integral equation using the Mellin transformation. The same study was developed by Dempsey et al. [9] for different punch profiles and by Woźniak et al. [10] for the case of Winkler type excavation. Birinci and Erdöl [11] investigated the contact problem of a double layer resting on a Winkler foundation. Both continuous and discontinuous cases are considered using Fourier transform. Çömez [12] investigated the contact problem of an FG layer supported by a Winkler-type foundation when the layer is pressed by a rigid cylindrical punch. Matysiak et al. [13] investigated the stress distribution in a layer lying on a hollow Winkler foundation using Fourier transform methods. A second-type integral equation is obtained by applying the boundary condition and Fourier transform of the problem. Çömez and Omurtag [14] investigated the contact problem of a Winkler–Pasternak-based FG orthotropic layer when the layer is pressed with a cylindrical or flat punch. The dynamic interaction between soil–foundation interaction has long been a subject of great interest. Dynamic loads such as seismic loads and machine vibrations substantially affect the vibration of the foundation and should be considered in the analysis and design of structures.

The dynamic analysis of a rigid strip foundation subjected to harmonic time-dependent vertical, shear and moment forces and bonded to a half-plane was studied by Luco and Wetsmann [15]. The static and dynamic response of rigid strip foundations resting on the surface of any number of diagonal anisotropic soil layers was studied by Gazetas [16]. Dargush and Chopra [17] solved time-harmonic axisymmetric problems governed by Biot’s theory of dynamic poroelasticity using BEM. The dynamic analysis of a rigid strip foundation resting on a random anisotropic multilayer half-space was performed by Lin et al. [18] using the precision integration method. Han et al. [19] investigated the dynamic impedance of rigid foundation embedded in anisotropic multilayer soil through hybrid numerical method. Ai et al. [20] examined the vertical vibration of a massless flexible strip foundation connected to a transversely isotropic multilayer semi-plane using the Fourier transform. This work was extended to the case of a dynamic rigid rectangular plate by Ai and Ye [21] using the Bessel series.

Wang et al. [22] investigated the dynamic response of a half-plane covered with a homogeneous layer pressed by a harmonic Hertz load using the Helmholtz function and Fourier integral transform. This study was extended by Wang et al. [23] to the case where the system is pressed by a flat punch and the material is viscoelastic. Yang et al. [24] investigated the dynamic response of orthotropic layered media with imperfect interfaces between layers under time-harmonic loading using the Fourier transform. The horizontal and vertical vibration of rigid strip foundation on poroelastic or viscoelastic half-space was investigated by Zheng et al. Çömez [25] investigated the dynamic contact problem between a rigid flat punch and an orthotropic-coated viscoelastic half-space by applying Helmholtz functions and Fourier transform. The axisymmetric thermoelastic contact vibration of a rigid rotating spherical punch pressed into a homogeneous half-plane was investigated by Lv et al. [26] using the Hankel transform.

Although the dynamic behavior of a rigid flat punch resting on elastic materials has been investigated by many researchers, the studies on the dynamic contact mechanics of viscoelastic materials are quite limited. In addition, to the best of the researcher knowledge, the vertical vibration of a layer supported by a Winkler–Pasternak foundation has not been investigated. To fill this gap in the literature, the author presents analytically in this paper the dynamic contact problem between the rigid flat punch and an orthotropic viscoelastic half-plane resting on a Winkler–Pasternak foundation. Using Fourier transform, Helmholtz functions and the boundary of the contact problem, a first kind singular integral equation is obtained and solved numerically with the Gauss–Chebyshev integration formula.

2 Formulation of the problem

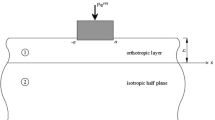
Figure 1 shows a viscoelastic orthotropic layer of height \(h\) lying on a two-parameter Winkler–Pasternak foundation. The layer is pressed with a flat punch of width \(2a\), which transmits a time harmonic an external excitation \(Pe^{i\omega t}\), where \(P\) is the amplitude of the load, \(\omega\) is the circular frequency of the load.

Fig. 1
figure 1

Geometry of the viscoelastic layer resting on a Winkler–Pasternak foundation

Full size image

The wave equations of elasto-dynamics can be written as:

$$\frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xz} }}{\partial z} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(1a)
$$\frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \sigma_{z} }}{\partial z} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(1b)

where \(u\),\(w\) are the \(x -\) and \(z -\) components of the displacement vector, \(\rho\) is the mass density and \(t\) denotes the time variable.

For the orthotropic layer, the stress–displacement relation can be written as follows:

$$\sigma_{x} = C_{11} \frac{\partial u}{{\partial x}} + C_{13} \frac{\partial w}{{\partial z}}$$
(2a)
$$\sigma_{z} = C_{13} \frac{\partial u}{{\partial x}} + C_{33} \frac{\partial w}{{\partial z}}$$
(2b)
$$\tau _{{xz}} = C_{{55}} \left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)$$
(2c)

The orthotropic layer is considered as a viscoelastic material, which can be described by a linear hysteretic dam** model. The hysteretic dam**, which can be described by the complex modulus, is assumed to occur in the orthotropic layer. The loss factor, \(\eta\), gives a measure of the natural dam** in a material when dynamically loaded. Accordingly, at a steady-state harmonic motion, the complex modulus can be expressed as \(C_{ij} = C_{ij}^{*} (1 + i\eta_{1} )\) where \(C_{ij}^{*}\) are the elastic constants:

$$C_{11}^{*} = - \frac{{E_{xx}^{*} (\nu_{xz} + \nu_{xy} \nu_{yz} )}}{\Delta },C_{13}^{*} = - \frac{{E_{xx}^{*} ( - 1 + \nu_{xy} \nu_{yx} )}}{\Delta },C_{33}^{*} = - \frac{{E_{zz}^{*} ( - 1 + \nu_{xy} \nu_{yx} )}}{\Delta },C_{55}^{*} = G_{xz}^{*}$$
(3)

where

$$\Delta = - 1 + \nu_{xy} (\nu_{yx} + \nu_{yz} \nu_{zx} ) + \nu_{yz} \nu_{zy} + \nu_{xz} (\nu_{zx} + \nu_{yx} \nu_{zy} )$$
(4a)
$$\nu_{yx} = \nu_{xy} \frac{{E_{yy}^{*} }}{{E_{xx}^{*} }},\nu_{zx} = \nu_{xz} \frac{{E_{zz}^{*} }}{{E_{zz}^{*} }},\nu_{zy} = \nu_{xz} \frac{{E_{zz}^{*} }}{{E_{yy}^{*} }}$$
(4b)

Inserting Eq. (2) into Eq. (1), the following governing equations for displacement are obtained

$$C_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + C_{55} \frac{{\partial^{2} u}}{{\partial z^{2} }} + (C_{13} + C_{55} )\frac{{\partial^{2} w}}{\partial x\partial z} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(5a)
$$(C_{13} + C_{55} )\frac{{\partial^{2} u}}{\partial x\partial z} + C_{55} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33} \frac{{\partial^{2} w}}{{\partial z^{2} }} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(5b)

To solve governing Eq. (5), the following Helmholtz functions can be presented:

$$u = \frac{\partial \phi }{{\partial x}} - \frac{\partial \psi }{{\partial z}},w_{j} = \frac{{\partial \phi_{j} }}{\partial z} + \frac{{\partial \psi_{j} }}{\partial x}$$
(6)

In a steady time-harmonic motion, the potential Helmholtz functions can be written in the harmonic form as follows:

$$\phi (x,z,t) = \phi^{(0)} (x,z)e^{i\omega t} ,\psi_{j} (x,z,t) = \psi^{(0)} (x,z)e^{i\omega t}$$
(7)

where \(\phi^{(0)} (x,z)\) and \(\psi_{{}}^{(0)} (x,z)\) are the complex amplitudes of potential functions.

Substituting (6 and 7) into the (5), the following partial differential equation system can be obtained depending on Helmholtz potential functions:

$$\begin{aligned} & - \rho_{1} \omega^{2} \frac{{\partial \psi^{(0)} }}{\partial z} - C_{55} \frac{{\partial^{3} \psi^{(0)} }}{{\partial z^{3} }} + ( - C_{11} + C_{13} + C_{55} )\frac{{\partial^{3} \psi^{(0)} }}{{\partial x^{2} \partial z}} + \rho_{1} \omega^{2} \frac{{\partial \phi^{(0)} }}{\partial x} \\ & \quad + (C_{13} + 2C_{55} )\frac{{\partial^{3} \phi^{(0)} }}{{\partial x\partial z^{2} }} + C_{11} \frac{{\partial^{3} \phi^{(0)} }}{{\partial x^{3} }} = 0 \\ \end{aligned}$$
(8a)
$$\begin{aligned} & \rho_{1} \omega^{2} \frac{{\partial \psi^{(0)} }}{\partial x} + C_{55} \frac{{\partial^{3} \psi^{(0)} }}{{\partial x^{3} }} - (C_{13} - C_{33} + C_{55} )\frac{{\partial^{3} \psi^{(0)} }}{{\partial x\partial z^{2} }} + \rho_{1} \omega^{2} \frac{{\partial \phi^{(0)} }}{\partial z} \\ & \quad + (C_{13} + 2C_{55} )\frac{{\partial^{3} \phi^{(0)} }}{{\partial x^{2} \partial z}} + C_{33} \frac{{\partial^{3} \phi^{(0)} }}{{\partial z^{3} }} = 0 \\ \end{aligned}$$
(8b)

The partial differential Eq. (8) can be transformed into an ordinary differential equation using the Fourier transform. For this purpose, the following Fourier transforms are defined:

$$\phi^{(0)} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\tilde{\phi }^{(0)} (k,z){\kern 1pt} e^{ - ikx} {\text{d}}k}$$
(9a)
$$\psi^{(0)} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\tilde{\psi }^{(0)} (k,z){\kern 1pt} e^{ - ikx} {\text{d}}k}$$
(9b)

where \(\tilde{\phi }^{(0)} (k,z)\) and \(\tilde{\psi }^{(0)} (k,z)\) are Fourier transforms of \(\phi^{(0)} (x,z)\) and \(\psi^{(0)} (x,z)\), respectively.

When Fourier transforms (9) are applied, Eq. (8) is reduced to the following system of ordinary differential equations

$$\begin{aligned} & i(C_{11} k^{3} - k\rho_{1} \omega^{2} )\tilde{\phi }^{(0)} + (C_{11} k^{2} - C_{13} k^{2} - C_{55} k^{2} - \rho_{1} \omega^{2} )\frac{{{\text{d}}\tilde{\psi }^{(0)} }}{{{\text{d}}z}} \\ & \quad - i(C_{13} + 2C_{55} )k\frac{{{\text{d}}^{2} \tilde{\phi }^{(0)} }}{{{\text{d}}z^{2} }} - C_{55} \frac{{{\text{d}}^{3} \tilde{\psi }^{(0)} }}{{{\text{d}}z^{3} }} = 0 \\ \end{aligned}$$
(10a)
$$\begin{aligned} & i(C_{55} k^{3} - k\rho_{1} \omega^{2} )\tilde{\psi }^{(0)} + ( - C_{13} k^{2} - 2C_{55} k^{2} + \rho_{1} \omega^{2} )\frac{{{\text{d}}\tilde{\phi }^{(0)} }}{{{\text{d}}z}} \\ & \quad + ik(C_{13} - C_{33} + C_{55} )\frac{{{\text{d}}^{2} \tilde{\psi }^{(0)} }}{{{\text{d}}z^{2} }}C_{55} \frac{{{\text{d}}^{3} \tilde{\psi }^{(0)} }}{{{\text{d}}z^{3} }} = 0 \\ \end{aligned}$$
(10b)

Upon solving the resulting equations, the following polynomial characteristic equation is obtained:

$$n^{4} + L_{1} n^{2} + L_{2} = 0$$
(11)

where

$$L_{1} = \frac{{(C_{13}^{2} - C_{11} C_{33} + 2C_{13} C_{55} )k^{2} + (C_{33} + C_{55} )\rho \omega^{2} }}{{C_{33} C_{55} }}$$
(12a)
$$L_{2} = \frac{{(C_{11} k^{2} - \rho_{1} \omega^{2} )(C_{55} k^{2} - \rho \omega^{2} )}}{{C_{33} C_{55} }}$$
(12b)

The roots of characteristic equation are:

$$n_{1,2} = \mp \frac{{\sqrt { - L_{1} - \sqrt { - 4L_{2} + L_{1}^{2} } } }}{\sqrt 2 },n_{3,4} = \mp \frac{{\sqrt { - L_{1} + \sqrt { - 4L_{2} + L_{1}^{2} } } }}{\sqrt 2 }$$
(13)

Thus, the solution of Eq. (10) may be expressed as:

$$\phi^{(0)} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ {\sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} } } \right\}} e^{ - ikx} {\text{d}}k$$
(14a)
$$\psi^{(0)} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right.} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} m_{s} e^{{\,n_{s} \,z}} } \left. \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right\}e^{ - ikx} dk$$
(14b)

where \(A{\kern 1pt}_{s}\) \((s = 1,2...4)\) are the initially unknown functions but can be found applying the boundary conditions of the problem.

where

$$m_{s} = \frac{{in_{s} ( - C_{13} k^{2} - 2C_{55} k^{2} + C_{33} n_{s}^{2} + \rho_{1} \omega^{2} )}}{{k( - C_{13} n_{s}^{2} - C_{33} n_{s}^{2} + C_{55} (k^{2} + n_{s}^{2} ) - \rho_{1} \omega^{2} )}}(s = 1,2...4)$$
(15)

Substituting Eq. (14) and Eq. (7) into Eq. (6), the displacement expressions for the orthotropic layer can be found as follows:

$$u(x,z,t) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ { - i\,e^{\,i\omega t} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} (k - i{\kern 1pt} m_{s} n_{s} )} } \right\}} e^{ - ikx} {\text{d}}k$$
(16a)
$$w(x,z,t) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right. - i} e^{\,i\omega t} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} (k{\kern 1pt} m_{s} + i{\kern 1pt} n_{s} )} \left. \begin{gathered} \hfill \\ \hfill \\ \end{gathered} \right\}e^{ - ikx} dk$$
(16b)

Substituting displacement expressions (16) into Eq. (2), the stress expressions for the layer can be written as follows:

$$\sigma_{x} (x,z,t) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ {e^{\,i\omega t} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} (C_{13} n_{s} ( - i{\kern 1pt} k{\kern 1pt} m_{s} + n_{s} ) - C_{11} k(k - i{\kern 1pt} m_{s} n_{s} ))} } \right\}} e^{ - ikx} {\text{d}}k$$
(17a)
$$\sigma_{z} (x,z,t) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ {e^{\,i\omega t} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} (C_{33} n_{s} ( - i\,k\,m_{s} + n_{s} ) - C_{13} k(k - i{\kern 1pt} \,m_{s} n_{s} ))} } \right\}} e^{ - ikx} {\text{d}}k$$
(17b)
$$\tau_{xz} (x,z,t) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left\{ { - e^{\,i\omega t} C_{55} \sum\limits_{s = 1}^{4} {A{\kern 1pt}_{s} e^{{\,n_{s} \,z}} (k^{2} m_{s} + 2i{\kern 1pt} k{\kern 1pt} n_{s} + m_{s} n_{s}^{2} )} } \right\}} e^{ - ikx} {\text{d}}k$$
(17c)

3 The boundary conditions and the singular integral equation

The boundary conditions for the orthotropic viscoelastic layer supported by a Winkler–Pasternak foundation can be defined as follows:

$$\sigma_{z} (x,0,t) = - p(x)e^{i\omega t} - a \le x \le a$$
(18a)
$$\tau_{xz} (x,0,t) = 0 - \infty < x < \infty$$
(18b)
$$\tau_{xz} (x, - h,t) = 0 - \infty < x < \infty$$
(18c)
$$\sigma_{z} (x, - h,t) = k_{{\text{w}}} w(x, - h,t) - k_{{\text{p}}} \frac{\partial w(x, - h,t)}{{\partial x}} - \infty < x < \infty$$
(18d)

where \(p(x){\kern 1pt}\) is the unknown contact stress under the rigid flat punch on the contact area \(( - a,a)\). \(k_{{\text{w}}}\) and \(k_{{\text{p}}}\) are Pasternak moduli, where the former being the subgrade reaction modulus and the latter is the shear foundation modulus.

When the Fourier transform is applied to the boundary conditions (18) and the resultant conditions are used, the coefficients \(A{\kern 1pt}_{s}\) \((s = 1,2...4)\), \(B_{1}\) and \(B_{2}\) can be found depending on the unknown contact stress and width as follows.

$$A{\kern 1pt}_{s} = A_{s}^{p} \int\limits_{ - a}^{a} {p(\xi )} {\text{d}}\xi ,B{\kern 1pt}_{j} = B_{j}^{p} \int\limits_{ - a}^{a} {p(\xi )} {\text{d}}\xi$$
(19)

Statements \(A_{s}^{p}\) and \(B_{j}^{p}\) are not given here because they are too long.

Substituting \(A{\kern 1pt}_{s}\), \(B_{1}\) and \(B_{2}\) into the mixed boundary conditions

$$\begin{array}{*{20}c} {\frac{dw(x,0,t)}{{dx}} = 0} & { - a < x < a} \\ \end{array}$$
(20)

The following equation can be obtained:

$$\frac{1}{2\pi }\int\limits_{ - a}^{a} {p(\xi ){\text{d}}\xi } \left[ {\int\limits_{ - \infty }^{\infty } {M_{1} (k)e^{ik(\xi - x)} {\text{d}}k} } \right] = 0$$
(21)

where

$$M_{1} (k) = ke^{\,i\omega t} \sum\limits_{s = 1}^{4} {A_{s}^{p} e^{{\,n_{s} \,h}} (k\,m_{s} + i\,n_{s} )}$$
(22)

Equation (21) can be rewritten as follows when the integral is put in the interval \(0 < x < \infty\)

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(\xi ){\text{d}}\xi } \int\limits_{0}^{\infty } {\left[ {i{\text{Re}} [M_{1} (k)] - {\text{Im}} [M_{1} (k)]} \right]\sin [k(\xi - x)]{\text{d}}k = 0}$$
(23)

Note that the following singular terms appear in (23)

$$\beta_{1} = \mathop {\lim }\limits_{k \to \infty } {\text{Re}} [M_{1} (k)],\beta_{2} = \mathop {\lim }\limits_{k \to \infty } {\text{Im}} [M_{1} (k)]$$
(24)

When removing the singular terms in \(M_{1} (\xi )\), the following singular integral equation can be obtained:

$$\frac{1}{\pi }\int\limits_{ - a}^{a} {p(\xi ){\text{d}}\xi } \left[ {\frac{\beta }{\xi - x} + K_{1} (x,\xi )} \right] = 0( - a < x < a)$$
(25)

where

$$\beta = i\beta_{1} - \beta_{2}$$
(26a)
$$K_{1} (x,\xi ) = \int\limits_{0}^{\infty } {\left[ {i\left\{ {{\text{Re}} [M_{1} (k)] - \beta_{1} } \right\} - \left\{ {{\text{Im}} [M_{1} (k)] - \beta_{2} } \right\}} \right]} \sin \left[ {k(\xi - x)} \right]{\text{d}}k$$
(26b)

The solution of the singular integral equation must satisfy the following equilibrium condition:

$$\int\limits_{ - \infty }^{\infty } {\sigma_{z} (x,h){\text{d}}x} = - \int\limits_{ - a}^{a} {p(\xi ){\text{d}}\xi } = - P$$
(27)

4 On the solution of the singular integral equation

Since the flat punch has sharp edge at the ends \((x = \mp a)\), the index of the integral equation Eq. (25) is “0” [27]. To normalize the size of rigid punch, we define.

$$\xi = a{\kern 1pt} r,x = a{\kern 1pt} s$$
(28)

Hence, Eq. (25) and Eq. (27) can be rewritten in the following form:

$$\frac{1}{\pi }\int\limits_{ - 1}^{1} {p(\xi ){\text{d}}\xi } \left[ {\frac{\beta }{r - s} + a{\kern 1pt} K_{1} (s,r)} \right] = 0$$
(29a)
$$a\int\limits_{ - 1}^{1} {p(r){\text{d}}r} = P$$
(29b)

Utilizing Gauss–Chebyshev integration formulas [27], the solution of the singular integral equation Eq. (29) can be written as:

$$p(r) = \frac{g(r)}{{\sqrt {1 - r^{2} } }}$$
(30)

Thus, Eq. (29) becomes

$$\frac{1}{N}\sum\limits_{m = 1}^{N} {g(r_{m} )\left[ {\frac{\beta }{{r_{m} - s_{k} }} + a{\kern 1pt} K_{1} (s_{k} ,r_{m} )} \right]} = 0k = 1,2...N - 1$$
(31a)
$$a\frac{1}{N}\sum\limits_{m = 1}^{N} {g(r_{m} ) = \frac{P}{\pi }} ,$$
(31b)

where

$$r_{i} = \cos \left( {\frac{2i - 1}{{2N}}\pi } \right)i = 1,2...N$$
(32a)
$$s_{k} = \cos \left( {\frac{k}{N}\pi } \right)k = 1,2...N - 1$$
(32b)

Equation (31) gives \(N\) equations to determine the \(N\) unknowns \(g(r_{m} )\).

After determining the contact stress, the in-plane stress \(\sigma_{x1} (x,h)\) can be obtained as follows:

$$\sigma_{x} (x,0) = \beta_{3} p(x) + \frac{1}{\pi }\int\limits_{ - 1}^{1} {p(\xi )d\xi } \left[ {a\,K_{2} (s,r)} \right]$$
(33)

where

$$K_{2} (x,\xi ) = \int\limits_{0}^{\infty } {\left[ {\left\{ {{\text{Re}} [M_{2} (k)] - \beta_{3} } \right\} + i{\text{Im}} [M_{2} (k)]} \right]} \cos [k(\xi - x)]{\text{d}}k$$
(34a)
$$M_{2} (k) = \sum\limits_{s = 1}^{4} {A_{s}^{p} e^{{n_{s} \,h}} \left( {C_{13} n_{s} ( - i{\kern 1pt} k{\kern 1pt} m_{s} + n_{s} ) - C_{11} k(k - i{\kern 1pt} m_{s} n_{s} )} \right)}$$
(34b)
$$\beta_{3} = \mathop {\lim }\limits_{k \to \infty } {\text{Re}} [M_{2} (k)]$$
(34c)

5 Numerical results

In this chapter, the dynamic response of a viscoelastic orthotropic sheet supported by a Winkler–Pasternak foundation is discussed. The effect of external excitation frequency \(\omega_{0} = \omega h\sqrt {\frac{\rho }{{C_{55}^{*} }}}\), loss factor \(\eta\), height of the layer \(h\), punch length \(a\), Winkler modulus \(k_{w}\) and Pasternak foundation modulus \(k_{p}\) on the absolute value of dynamic contact stress \(\left| {p(x)} \right|\) is illustrated in figures. Before the numerical solution, the kernels of the integral equations from which the singular term is removed are plotted and their convergence to zero is determined.

The effect of the excitation frequency \(\omega_{0}\) on the absolute values of the contact stress \(\left| {p(x)} \right|\) is given in Fig. 2. As expected, due to the sharp corners of the punch, the contact stress goes to infinity at the point where the contact ends. The distribution of the contact stress is almost uniform in the static state, i.e., at \(\omega_{0} = 0\). From the figure, it can be concluded that the dynamic behavior of the contact stress becomes increasingly oscillatory as the external excitation frequency increases.The dynamic contact stress at the center of the punch is smallest in the static state and decreases with increasing excitation frequency.

Fig. 2
figure 2

The effect of the excitation frequency \(\omega_{0}\) on the absolute values of contact stress \(\left| {p(x)} \right|\) \((\eta_{1} = 0.01,a = 0.001\,{\text{m}},h = 0.001\,{\text{m}},k_{{\text{w}}} = 100 \times 10^{6} {\text{N}}/{\text{m}}^{3} ,k_{{\text{p}}} = 500 \times 10^{6} {\text{N}}/{\text{m}}^{2} )\)

Full size image

Figures 3 and 4 show the effect of the Winkler–Pasternak basic parameters \(k_{{\text{w}}}\) and \(k_{{\text{p}}}\) on the absolute values of the contact stress \(\left| {p(x)} \right|\), respectively. The contact stress is insensitive to the variation of the Winkler foundation parameter \(k_{{\text{w}}}\). However, the influence of the Pasternak foundation modulus \(k_{{\text{p}}}\) on the contact stress is clear. The oscillatory characteristic of the contact stress becomes more pronounced as w decreases. The maximum values of the dynamic contact stress at the center of the rigid staple increase as the Pasternak basic modulus decreases.

Fig. 3
figure 3

The effect of the Winkler foundation modulus \(k_{w}\) on the absolute values of contact stress \(\left| {p(x)} \right|\) \((\omega_{0} = 2,\eta = 0.01,a = 0.003\,{\text{m}},h = 0.002\,{\text{m}},k_{{\text{p}}} = 500 \times 10^{6} {\text{N}}/{\text{m}}^{2} )\)

Full size image
Fig. 4
figure 4

The effect of the Pasternak foundation modulus \(k_{p}\) on the absolute values of contact stress \(\left| {p(x)} \right|\) \((\omega_{0} = 2,\eta = 0.01,a = 0.003\,{\text{m}},h = 0.002\,{\text{m}},k_{{\text{w}}} = 100 \times 10^{6} {\text{N}}/{\text{m}}^{3} )\)

Full size image

The effect of layer height \(h\) on the absolute values of the contact stress is shown in Fig. 4. The dynamic behavior of the contact stress becomes increasingly oscillatory as the layer height increases. This is because the dynamic external load approaches the Winkler–Pasternak basis as the layer depth decreases. When the layer depth is smallest, the stress is highly fluctuating. The largest stress in the center of the punch occurs when the height is the highest and decreases as the height decreases (Fig. 5).

Fig. 5
figure 5

The effect of the layer height \(h\) on the absolute values of contact stress \(\left| {p(x)} \right|\)\((\omega_{0} = 2,\eta = 0.01,a = 0.003\,{\text{m}},k_{{\text{w}}} = 100 \times 10^{6} {\text{N}}/{\text{m}}^{3} ,k_{{\text{p}}} = 500 \times 10^{6} {\text{N}}/{\text{m}}^{2} )\)

Full size image

Figure 6 presents the effect of the punch length \(a\) on the absolute values of contact stress. The behavior of the punch length on the contact stress is the inverse of the layer height. That is, when the punch length increases, dynamic behavior is clearly manifested, and the contact stress becomes fluctuating. Since the stress is distributed over a larger area and since the stress is distributed over a larger area, a decrease in the punch length reduces the contact stress at the center of the staple.

Fig. 6
figure 6

The effect of the punch length \(a\) on the absolute values of contact stress \(\left| {p(x)} \right|\)\((\omega_{0} = 2,\eta = 0.01,h = 0.002\,{\text{m}},k_{{\text{w}}} = 100 \times 10^{6} {\text{N}}/{\text{m}}^{3} ,k_{{\text{p}}} = 500 \times 10^{6} {\text{N}}/{\text{m}}^{2} )\)

Full size image

The variation of dynamic contact stress with loss factor \(\eta\) is shown in Fig. 7. The dynamic contact stress is almost insensitive except in the case of \(\eta = 0.05\).

Fig. 7
figure 7

The effect of the loss factor \(\eta\) on the absolute values of contact stress \(\left| {p(x)} \right|\)\((\omega_{0} = 2,a = 0.003\,{\text{m}},h = 0.002\,{\text{m}},k_{{\text{w}}} = 100 \times 10^{6} {\text{N}}/{\text{m}}^{3} ,k_{{\text{p}}} = 500 \times 10^{6} {\text{N}}/{\text{m}}^{2} )\)

Full size image

6 Conclusions

In this study, the contact response of a viscoelastic orthotropic layer indented by a harmonic vertical load is presented. The layer is indented by a rigid flat punch, and the foundation is modeled as a two-parameter Winkler–Pasternak-type foundation. By applying the Fourier transform, Helmholtz functions and the boundary of the contact problem, a Couch-type singular integral equation is obtained and numerically treated with the Gauss–Chebyshev integration formula. The effects of external excitation frequency, loss factor, Winkler–Pasternak parameters, punch length and layer height on the dynamic contact stress are discussed. The results show that the dynamic behavior of the contact stress becomes increasingly oscillatory as the external excitation frequency increases.

  • Contact stress is insensitive to the change of Winkler foundation parameter. However, the oscillatory feature of contact stress becomes evident as Pasternak modulus decreases.

  • The dynamic contact stress is almost insensitive to the change of loss factor.

  • The greatest stress in the middle of the punch occurs when the height is the highest and decreases as the height decreases.

  • When the punch length increases, dynamic behavior clearly occurs, and the contact stress becomes fluctuating.