Assessing the effects of time series on precipitation forecasting performance from complexity perspective

Abstract

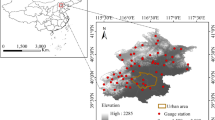
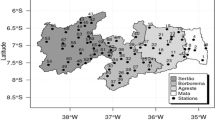
Affected by many factors, the precipitation time series have complex characteristics, which increases the difficulty of precipitation prediction. To reveal the impact of complexity on prediction performance, we propose an impact assessment framework. In this framework, firstly, the complexity results of four commonly used entropy models are compared, and the suitable entropy for precipitation complexity is selected from the perspective of stability and reliability. Secondly, the typical machine learning models (multiple linear regression, support vector machine regression, and BP artificial neural network) are used to predict precipitation. Three regions (including 44 meteorological stations) were selected for the study. The results show that (1) the (sample entropy) SE is higher than (wavelet entropy) WE, (permutation entropy) PE and (Fuzzy entropy) FE from the reliability and stability of the results; (2) there are differences in precipitation predictability at different complexity levels. For the high level of complexity, the prediction performance R² is even close to 0. In addition, the difficulty of precipitation predictability in Southeast China is much higher than that in the other two regions. The findings of this research can help forecasters in determining the difficulty of regional precipitation predictability.

Appendix

1.1 Permutation entropy

The main idea of PE is that the patterns within the time series do not have similar probability of occurrence (Bandt and Pompe 2002). The calculation process is as follows:

Given a time series z(i) , the phase space reconstruction is performed to obtain the reconstructed vector and form the phase space matrix:

$$Z(i)=\left[\begin{array}{cccc}z(1)& z\left(1+\tau \right)& \cdots & z\left(1+\left(m-1\right)\tau \right)\\ {}\vdots & \vdots & \cdots & \vdots \\ {}z(j)& z\left(j+\tau \right)& \cdots & z\left(j+\left(m-1\right)\tau \right)\\ {}\vdots & \vdots & \cdots & \vdots \\ {}z(G)& z\left(G+\tau \right)& \cdots & z\left(G+\left(m-1\right)\tau \right)\end{array}\right]$$

(A.1)

where, m denotes the embedding dimension, τ denotes the delay time, and G denotes the number of vectors in phase space reconstruction.

Each reconstruction vector in the Z(i) is arranged in ascending order to obtain the following formula:

$$\left\{z\left(i+\left({j}_1-1\right)\tau \right)\le z\left(i+\left({j}_2-1\right)\tau \right)\le \cdots \le z\left(i+\left({j}_m-1\right)\tau \right)\right\}$$

(A.2)

where, j₁, j₂, ⋯j_m is the index of the reconstructed component in the column of each element.

For any reconstruction vector z(j) in the phase space matrix, a symbol sequence S(l) = {j₁, j₂, ⋯, j_m} can be obtained after ascending, where l = 1, 2, …, g, g ≤ m!. S(l) is one of the arrangements, and then calculate the probability of each coincidence sequence P_g. The calculation formula of PE can be written as (Bandt and Pompe 2002):

$$PE(m)=-\sum_{l=1}^g{P}_l\ln {P}_l$$

(A.3)

1.2 Wavelet entropy

The WE is a kind of entropy value calculated by wavelet decomposition of signal sequence, which reflects a measure of the ordered or disordered state of signal spectral energy distribution in each subspace (Rosso et al. 2001). The specific calculation steps are as follows:

The signal uses discrete wavelet transform to separate the low frequency band of the signal from the high frequency band, and decomposes the signal into detail coefficients (D_{j, k}) and approximate coefficients (A_{j, k}):

$$\left\{\begin{array}{c}{D}_{j,k}=\sum_n\overline{g}\left(n-2k\right){D}_{j-1,n}\\ {}{A}_{j,k}=\sum_n\overline{h}\left(n-2k\right){A}_{j-1,n}\end{array}\right.$$

(A.4)

where, j is the decomposition level, k is the corresponding wavelet coefficient subscript; g(n) and h(n) are high-pass and low-pass filters, respectively.

The subband energy of the signal is calculated by the square sum of the subband wavelet coefficients:

$${E}_j=\sum_k{\left|{D}_{j,k}\right|}^2$$

(A.5)

Calculate the total wavelet energy and relative wavelet energy (p_j):

$$\left\{\begin{array}{c}{E}_{total}=\sum_j{E}_j\\ {}{p}_j=\frac{E_j}{E_{total}}\end{array}\right.$$

(A.6)

Calculate the WE:

$$WE=-\sum_j{p}_j\ln {p}_j$$

(A.7)

1.3 Sample entropy

The SE is the probability of generating a new subsequence in the detection time series. The higher the SE, the more complex the sample sequence (Richman and Randall 2000). The calculation process is as follows:

For the time series {x(n)} = {x(1), x(2), …x(N)} composed of N data, it is composed of m-dimensional vectors X_m(1), ⋯X_m(N − m + 1).

$$\textrm{where},{X}_m(i)=\left\{x(i),x\left(i+1\right),\cdots x\left(i+m-1\right)\right\},\left(1\le i\le N-m+1\right).$$

Defines the maximum difference between the elements corresponding to the vectors X_m(i) and X_m(j).

Determine the SE:

$$\left\{\begin{array}{c}{A}^k(r)=\frac{1}{N-m}\sum\limits_{i=1}^{N-m}\frac{1}{N-m-1}{A}_i\\ {}{B}^m(r)=\frac{1}{N-m}\sum\limits_{i=1}^{N-m}\frac{1}{N-m-1}{B}_i\\ {} SE=-\ln \left\{\frac{A^m(r)}{B^m(r)}\right\}\end{array}\right.$$

(A.8)

Where, A_i is the number of X_m + 1(i) and X_m + 1(j)(1 ≤ j ≤ N = m, j ≠ i) distance not greater than r ; B_i is the number of X_m(i) and X_m(j) distance not greater than r.

1.4 Fuzzy entropy

The FE is used to characterize the complexity of time series. The greater the entropy, the greater the complexity. FE is a very important nonlinear analysis method, which is less sensitive to parameter changes and less dependent on data length (Luca and Termini 1972). The calculation process is as follows:

Given the time series {x(i), i = 1, 2, ⋯, N}, the similarity tolerance r is introduced to determine a degree m(m ≤ N − 2) that divides the length of the subsequence, and the original sequence is reconstructed to obtain (N − m + 1) subsequences:

$$\left\{\begin{array}{c}X(1),X(2),\cdots X\left(N-m+1\right)\\ {}X(i)=\left[x(i),x\left(i+1\right),\cdots, x\left(i+m-1\right)\right]-{x}_0(i)\\ {}{x}_0(i)=\frac{1}{m}\sum\limits_{j=0}^{m-1}x\left(i+j\right)\end{array}\right.$$

(A.9)

The fuzzy membership function is introduced:

$${A}_{ij}^m=\exp \left[-{\left(\frac{d_{ij}^m}{r}\right)}^n\right]$$

(A.10)

where, ${d}_{ij}^m=d\left[X(i),X(j)\right]$ represents the maximum absolute distance between two reconstructed vectors, determined by the maximum difference of corresponding position elements. n represents the fuzzy power (it is usually equal to 2).

Take the average for each i:

$${C}_i^m(r)=\frac{1}{N-m}\sum_{j=1,j\ne i}^{N-m+1}{A}_{ij}^m$$

(A.11)

Define the fuzzy entropy intermediate quantity:

$${\varPhi}^m(r)=\frac{1}{N-m+1}\sum_{i=1}^{N-m+1}{C}_i^m(r)$$

(A.12)

Repeat the above steps to obtain Φ^m +1(r) when m + 1, so the FE of time series are as follows:

$$FE=\ln {\varPhi}^{m+1}(r)-\ln {\varPhi}^m(r)$$

(A.13)