Spatio-temporal analysis of particulate matter extremes in Seoul: use of multiscale approach

Abstract

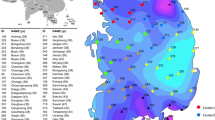
This paper considers a problem of analyzing temporal and spatial structure of particulate matter (PM) data with emphasizing high-level $\text {PM}_{10}$. The proposed method is based on a combination of a generalized extreme value (GEV) distribution and a multiscale concept from scaling property theory used in hydrology. In this study, we use hourly $\text {PM}_{10}$ data observed for 5 years on 25 stations located in Seoul metropolitan area, Korea. For our analysis, we calculate monthly maximum values for various duration times and area coverages at each station, and show that their distribution follows a GEV distribution. In addition, we identify that the GEV parameters of $\text {PM}_{10}$ maxima hold a new scaling property, termed ‘piecewise linear scaling property’ for certain duration times. By using this property, we construct a 12-month return level map of hourly $\text {PM}_{10}$ data at any arbitrary d-hour duration. Furthermore, we extend our study to understand spatio-temporal multiscale structure of $\text {PM}_{10}$ extremes over different temporal and spatial scales.

Appendices

Appendix 1: scaling property theory

Scaling property is widely used in multiscale rainfall analysis, which explains the relation between $Y_{d}(x)$ and $Y_{d_{ref}}(x)$. We consider a nonnegative random variable Y only. Evenly-time-spaced climate data including $\text {PM}_{10}$ extremes have their own reference observational time such as a hour, a month, etc. In this paper, the reference time is considered as a hour since the $\text {PM}_{10}$ data are observed at every hour. Let $Z_{d}(x)$ be a maximum of $Y_{d}(x)$, d hour duration $\text {PM}_{10}$ density at location x. We are interested in the distribution of $Z_{d}(x)$. When the information of the distribution is known, we have the information about quantiles of $Z_{d}(x)$; hence, we could compute the extreme $\text {PM}_{10}$ intensity at any observation location and/or duration time.

On the other hand, a wide-sense scaling property between $Y_{d_{ref}}(x)$ and $Y_{d}(x)$ is expressed by the following equation (Gupta and Waymire 1990; Menabde et al. 1999)

$$\begin{aligned} Y_{d}(x)\mathop {=}\limits ^{d}\left(\frac{d}{d_{ref}}\right)^{-\nu }Y_{d_{ref}}(x), \end{aligned}$$

where $\frac{d}{d_{ref}}$ is a scaling factor and $\nu$ is a scaling exponent. The meaning of this simple scaling property is that $(\frac{d}{d_{ref}})^{-\nu }Y_{d_{ref}}(x)$ and $Y_{d}(x)$ are equal in distribution. Thus, if we know the distribution of $Y_{d_{ref}}(x)$, the scaling factor and the scaling exponent, then it is able to obtain the distribution of $Y_{d}(x)$ as well. This property also holds for $Z_{d}(x)$, that is,

$$\begin{aligned} Z_{d}(x)\mathop {=}\limits ^{d}\left(\frac{d}{d_{ref}}\right)^{-\nu }Z_{d_{ref}}(x). \end{aligned}$$

The role of the scaling exponent can be interpreted as follows. When the scaling exponent is less than zero, $d>d_{ref}$ implies $Z_{d}(x)>Z_{d_{ref}}(x)$, while when the scaling exponent is bigger than zero, $d<d_{ref}$ indicates $Z_{d}(x)<Z_{d_{ref}}(x)$.

On the other hand, a strict-sense scaling property is defined by cumulative distribution function (CDF) of Y, F

$$\begin{aligned} F_{d}(x)=F_{d_{ref}}\left(\left(\frac{d}{d_{ref}}\right)^{\nu }x\right), \end{aligned}$$

(8)

where $F_{Y_{d}}$ and $F_{Y_{d_{ref}}}$ are CDFs of GEV ($\mu _{d}, \sigma _{d}, \xi _{d}$) and GEV ($\mu _{d_{ref}}, \sigma _{d_{ref}}, \xi _{d_{ref}}$), respectively. With the assumption of $\xi _{d}=\xi _{d_{ref}}=\xi$, we derive the following scaling equation between GEV parameters from (8)

$$\begin{aligned} \mu _{d}=\mu _{d_{ref}}\times (d/d_{ref})^{-\nu }\quad \text {and}\quad \sigma _{d}=\sigma _{d_{ref}}\times (d/d_{ref})^{-\nu }, \end{aligned}$$

which is used for estimating $\mu _{d}$ and $\sigma _{d}$ from $\mu _{d_{ref}}$, $\sigma _{d_{ref}}$ and $\nu$.

Appendix 2: generalized extreme value distribution

GEV distribution is known that it is suitable for fitting blockwise extreme value distribution such as a distribution of monthly $\text {PM}_{10}$ maxima. The probability density function (PDF) of GEV distribution is defined as

$$\begin{aligned} f(s;\mu ,\sigma ,\xi )=\frac{1}{\sigma }t(x)^{\xi +1}e^{-t(x)}, \end{aligned}$$

where

$$\begin{aligned} t(x)= {\left\{ \begin{array}{ll} \left(1+(\frac{x-\mu }{\sigma })\xi \right)^{-1/\xi } & \quad \text {if }\quad \xi \ne 0\\ e^{-(x-\mu )/\sigma } & \quad \text {if }\quad \xi = 0.\\ \end{array}\right. } \end{aligned}$$

Here $\mu$, $\sigma$, $\xi$ denote location, scale and shape parameters, respectively. The corresponding CDF is

$$\begin{aligned} F(x;\mu ,\sigma ,\xi )=\exp \left( -\left(1+\xi\left(\frac{x-\mu }{\sigma }\right)\right)^{-1/\xi }\right) . \end{aligned}$$

The location and scale parameters of GEV have similar roles with those in normal distribution. The sign of the shape parameter decides GEV family types. Figure 14 shows the three types of GEV class by changing sign of the shape parameter: when the sign is zero, it is called Gumbel family, when the sign is positive, it is called Fréchet family, and when the sign is negative, it is called Weibull family. Note that for computation of GEV, we use maximum likelihood fitting for GEV in R package ismev of Heffernan and Stephenson (2016).

Fig. 14

GEV distribution at $\mu =0$, $\sigma =1$ with different shape parameters, $\xi =-0.5$ (green), $\xi =0$ (red) and $\xi =0.5$ (blue)