Isogeometric analysis of shear-deformable, in-plane functionally graded microshells by Mindlin’s strain gradient theory

Abstract

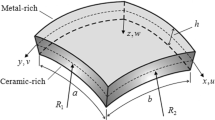
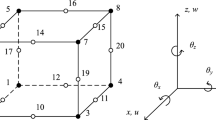
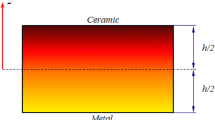
This paper proposes a general strain-gradient and shear-deformable isogeometric microshell formulation based on the complete Mindlin’s form II strain gradient theory (SGT) and Reissner–Mindlin shell model for the static and dynamic analyses of in-plane functionally graded (IFG) microshell structures. The material properties are assumed to vary along in-plane directions and are effectively homogenized via the rule of mixture. Within the Galerkin weak form, tensor-based governing equations of motion expressed in natural curvilinear coordinates are first formulated and accordingly solved by a non-uniform rational basis spline-based isogeometric analysis (IGA) approach. As its general characteristics, the numerical formulation can not only accurately simulate the size-dependent behaviors of thin to moderately thick IFG microshells with arbitrary shapes and material gradation patterns but also effectively provide the predictions of different reduced SGT-based theories, i.e., the modified strain gradient, modified couple stress, and simplified strain gradient theories. These features are confirmed using selected examples related to static, free vibration, and transient dynamic problems. The presented formulation is expected to serve as a comprehensive and reliable instrument to assist the design of advanced thin-walled components and further interpret different aspects of their underlying theory.

Appendices

Appendix 1: Expressions of classical and non-classical material moduli matrices

The classical material moduli matrices ${{\varvec{C}}}_{1}$ and ${{\varvec{C}}}_{2}$ are expressed as follows:

$${\mathbf{C}}_{1}=\left[\begin{array}{ccc}{\widehat{C}}^{1111}& {\widehat{C}}^{1122}& {\widehat{C}}^{1112}\\ {\widehat{C}}^{2211}& {\widehat{C}}^{2222}& {\widehat{C}}^{2212}\\ {\widehat{C}}^{1211}& {\widehat{C}}^{1222}& {\widehat{C}}^{1212}\end{array}\right], {\mathbf{C}}_{2}=\left[\begin{array}{cc}{\widehat{C}}^{1313}& {\widehat{C}}^{1323}\\ {\widehat{C}}^{2313}& {\widehat{C}}^{2323}\end{array}\right],$$

(86)

where the components ${\widehat{C}}^{ijkl}$ are computed using Eq. (22).

The non-classical material moduli matrices are given as follows:

$${\mathbf{D}}_{11}=\left[\begin{array}{cccccc}{\widehat{D}}^{111111}& {\widehat{D}}^{111122}& {\widehat{D}}^{111112}& {\widehat{D}}^{111211}& {\widehat{D}}^{111222}& {\widehat{D}}^{111212}\\ {\widehat{D}}^{122111}& {\widehat{D}}^{122122}& {\widehat{D}}^{122112}& {\widehat{D}}^{122211}& {\widehat{D}}^{122222}& {\widehat{D}}^{122212}\\ {\widehat{D}}^{112111}& {\widehat{D}}^{112122}& {\widehat{D}}^{112112}& {\widehat{D}}^{112211}& {\widehat{D}}^{112222}& {\widehat{D}}^{112212}\\ {\widehat{D}}^{211111}& {\widehat{D}}^{211122}& {\widehat{D}}^{211112}& {\widehat{D}}^{211211}& {\widehat{D}}^{211222}& {\widehat{D}}^{211212}\\ {\widehat{D}}^{222111}& {\widehat{D}}^{222122}& {\widehat{D}}^{222112}& {\widehat{D}}^{222211}& {\widehat{D}}^{222222}& {\widehat{D}}^{222212}\\ {\widehat{D}}^{212111}& {\widehat{D}}^{212122}& {\widehat{D}}^{212112}& {\widehat{D}}^{212211}& {\widehat{D}}^{212222}& {\widehat{D}}^{212212}\end{array}\right],$$

(87)

$${\mathbf{D}}_{14}=[{\mathbf{D}}_{41}{]}^{\rm T}=\left[\begin{array}{cc}{\widehat{D}}^{111133}& {\widehat{D}}^{111233}\\ {\widehat{D}}^{122133}& {\widehat{D}}^{122233}\\ {\widehat{D}}^{112133}& {\widehat{D}}^{112233}\\ {\widehat{D}}^{211133}& {\widehat{D}}^{211233}\\ {\widehat{D}}^{222133}& {\widehat{D}}^{222233}\\ {\widehat{D}}^{212133}& {\widehat{D}}^{212233}\end{array}\right], {\mathbf{D}}_{22}=\left[\begin{array}{ccc}{\widehat{D}}^{311311}& {\widehat{D}}^{311322}& {\widehat{D}}^{311312}\\ {\widehat{D}}^{322311}& {\widehat{D}}^{322322}& {\widehat{D}}^{322312}\\ {\widehat{D}}^{312311}& {\widehat{D}}^{312322}& {\widehat{D}}^{312312}\end{array}\right],$$

(88)

$${\mathbf{D}}_{23}={\mathbf{D}}_{32}^{\rm T}=\left[\begin{array}{cccc}{\widehat{D}}^{311113}& {\widehat{D}}^{311123}& {\widehat{D}}^{311213}& {\widehat{D}}^{311223}\\ {\widehat{D}}^{322113}& {\widehat{D}}^{322123}& {\widehat{D}}^{322213}& {\widehat{D}}^{322223}\\ {\widehat{D}}^{312113}& {\widehat{D}}^{312123}& {\widehat{D}}^{312213}& {\widehat{D}}^{312223}\end{array}\right],$$

(89)

$${\mathbf{D}}_{33}=\left[\begin{array}{cccc}{\widehat{D}}^{113113}& {\widehat{D}}^{113123}& {\widehat{D}}^{113213}& {\widehat{D}}^{113223}\\ {\widehat{D}}^{123113}& {\widehat{D}}^{123123}& {\widehat{D}}^{123213}& {\widehat{D}}^{123223}\\ {\widehat{D}}^{213113}& {\widehat{D}}^{213123}& {\widehat{D}}^{213213}& {\widehat{D}}^{213223}\\ {\widehat{D}}^{223113}& {\widehat{D}}^{223123}& {\widehat{D}}^{223213}& {\widehat{D}}^{223223}\end{array}\right],~ {\mathbf{D}}_{44}=\left[\begin{array}{cc}{\widehat{D}}^{133133}& {\widehat{D}}^{133233}\\ {\widehat{D}}^{233133}& {\widehat{D}}^{233233}\end{array}\right],$$

(90)

where the components ${\widehat{D}}^{ijklmn}$ are evaluated via Eq. (23).

Appendix 2: Sensitivity analysis for the penalty parameter

In this appendix, results from the sensitivity study to determine the sufficient range of the penalty parameter $\zeta$ for predicting accurate solutions of the static, free vibration, and transient dynamic problems are reported. For brevity, only representative cases corresponding to the static, free vibration, and transient analysis of homogeneous square microplate problems considered in Sects. 4.1.1, 4.2.1, and 4.3.1, respectively, are presented. In calculations, the same set of model parameters used previously are adopted.

First, Fig. 26 shows the variation of the normalized central deflection of the MCST-based microplate considered in Sect. 4.1.1 for a wide range of $\zeta$, ranging from 1 to 20. It can be seen from the presented results that the predicted response is not sensitive to $\zeta$, becoming unstable when using $\zeta >16$. Specifically, the obtained results from the present study exhibit an excellent agreement with the reference results by Thai and Choi [101] if $4\le \zeta \le 16$ is assigned.

Next, Table 6 presents the results of the first four normalized frequencies of the MSGT-based microplate with $1\le \zeta \le 10$ while Fig. 27 plots the transient response of the MCST-based microplate with different values of $\zeta$ (i.e., $\zeta \in \left\{\mathrm{2,4},\mathrm{6,8},10\right\}$). In contrast to the static problem, the range of $\zeta$ for predicting the accurate free vibration results of the MSGT-based microplate in comparison with the benchmark solutions reported by Torabi et al. [24] was reduced to $4\le \zeta \le 8$. Within this range, a good agreement between the results obtained from the present study and Mao et al. [74] for the transient response of the MCST-based homogeneous microplate was also observed. In general, using $4\le \zeta \le 8$ can result in accurate predictions for both static and dynamic problems. Similar observations were also found for the remaining microshell problems. Thus, the average of the range, i.e., $\zeta =6$, was chosen for imposing the BCs for the IFG microshell problems considered in the present study.

Fig. 26

Variation of the normalized central deflection of the MCST-based homogeneous simply supported microplate (considered in Sect. 4.1.1) with respect to the penalty parameter $\zeta$.

Table 6 Variation of the normalized frequencies of the MSGT-based homogeneous clamped microplate (considered in Sect. 4.2.1) with respect to the penalty parameter

Fig. 27

Transient response of the MCST-based homogeneous clamped microplate under a harmonic pressure (considered in Sect. 4.3.1) with different values of the penalty parameter $\zeta$