1 Introduction

Occasionally, the discussions about the interpretation of quantum mechanics seem to be a never-ending story [1]. A prominent example of this ongoing debate is the delayed choice 'Gedankenexperiment' [2] which has originally been proposed by Wheeler [3]. According to this scenario light strikes an optical beam splitter (BS1) and is divided into equal parts, a reflected and a transmitted beam with a detector for each (Fig. 1).

Fig. 1
figure 1

Optical beam splitter (BS1) A1, A2: input beams of BS1. A3, A4: output beams. Detectors D1 and D2

Full size image

An interesting situation arises when the light is dimmed down all the way to the point that only one photon at a time is present in the system. It seems that there are only two options for the photon, either to occupy the transmitted or the reflected beam, tertium non datur. Apparently, experiments confirm this expectation. With equal likelihood either detector D1 or detector D2 registers a photon. Depending on which detector has responded in an event people conclude that the path the photon had taken can be told.

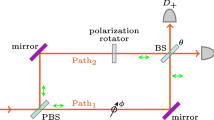
Now this arrangement is modified and two totally reflecting mirrors turn the beams by 90° so that they cross at some point downstream. A second beam splitter (BS2) is introduced at the crossing point, and the beams are recombined on the detectors, as shown in Fig. 2. This configuration is called a Mach–Zehnder interferometer. By changing the optical path lengths, a phase shift ф between the beams can be introduced. For example, the phase can be adjusted such that there is constructive interference at detector D1 and destructive interference at detector D2, i.e., all light is reaching D1 and no light D2. However, how can interference occur when only one photon is present, and this one is occupying the reflected or the transmitted beam? There is no light in the other channel to interfere with.

Fig. 2
figure 2

Mach–Zehnder interferometer B1, B2: input beams of the second beam splitter BS2. B3, B4: output beams

Full size image

People have come up with interpretations that the fundamental rules of logics are mysteriously broken and attribute to the photon some strange abilities. When arriving at the first BS the photon ‘senses’ whether a second BS is present. Depending on the result the photon ‘decides’ to go on one of the two tracks or elects to follow ‘both paths at the same time’ and ‘interfere with itself’. In the first case light exhibits corpuscular properties, while it behaves like a wave in the second case.

To clarify this mystery the following procedure has been considered [3]. An experiment is started in configuration of Fig. 2, but initially without the second BS. According to the decision hypothesis the photon must elect which way to follow. After this decision but before reaching the detector the second BS is introduced. What happens in this case when the choice to follow a specified scenario is delayed?

The actual experimental results show that interference does occur. It is experimentally confirmed that it does not matter if the ‘choice’ was delayed (see, for example, [4,5,6]). The result is the same, just as if the second BS had been present in the first place.

There have been numerous attempts [7] to interpret the delayed choice experiment occasionally contributing to the confusion over the wave-particle issue rather than settling it. Some of the interpretations suffer from misconceptions of the photon, attributing to it some properties of a classical particle, e.g., assigning to it a trajectory. The delayed choice experiment raises a new particularly strange aspect, that is, the apparent ability of the photon to change its own past [3].

On the other hand, the proper quantum treatment of interference [8] shows that the concept of entanglement plays a central role. Entanglement is a unique feature of quantum physics without equivalent in classical physics. In the case of the optical beam splitter the key point is that the reflected and the transmitted beam form an entangled quantum state. As a matter of principle, in such an entangled state the photon cannot be assigned to a specific track. There is no choice to be made.

This article is focussed on the quantum treatment of the optical beam splitter and of the Mach–Zehnder interferometer. The discussion of the delayed choice experiment will be restricted to the simple situation of the single photon input of the original ‘Gedanken-experiment’. On the other hand, there is a vast body of literature today on highly sophisticated extensions of delayed choice experiments including entangled input and delayed choice quantum erasing. A comprehensive review can be found in [2]. Popular accounts are available on various websites, e.g., [9, 10].

2 The optical beam splitter

Let us now consider again Fig. 1 and discuss the functioning of an optical BS. Two light beams with electrical fields \(E_{1}\) and \(E_{2}\) are incident on a partially transmitting mirror along channels A1 and A2 at angles of 45°. Let R and T be the complex reflection and transmission coefficient of the mirror. At this point the polarization of the light does not matter and is assumed to be perpendicular. The output fields \(E_{3}\) and \(E_{4}\) along channels A3 and A4 are given by the following relations:

$$\begin{aligned} E_{3} & = RE_{1} + TE_{2} \\ E_{4} & = TE_{1} + RE_{2} . \\ \end{aligned}$$
(1)

It is shown in [11] that for a lossless beam splitter energy conservation requires that the complex reflection and transmission coefficients satisfy the conditions \(\left| R \right|^{2} + \left| T \right|^{2} = 1\) and \(R\,\overline{T} + \overline{R}\,T\, = 0\). The bar over a symbol indicates complex conjugate.

It is well known that the electromagnetic field can be quantized by associating with each radiation mode a quantum mechanical harmonic oscillator with the corresponding creation and annihilation operators [12, 13]. It is assumed that each of the four channels of the BS represents a radiation mode. The corresponding creation operators are \(a_{1}^{ + } ,a_{2}^{ + } ,\,a_{3}^{ + } \,{\text{and}}\,\,a_{4}^{ + }\) and the annihilation counter parts \(a_{1}^{ - } ,a_{2}^{ - } ,\,a_{3}^{ - } \,{\text{and}}\,\,a_{4}^{ - }\).

Let \(\,\left| n \right\rangle_{\nu }\) represent the state vector of the \(\nu\)-channel occupied by n photons. The action of the operators is given by the well-known harmonic oscillator relations:

$$\begin{aligned} a_{\nu }^{ + } \left| n \right\rangle_{\nu } & = \sqrt {n + 1} \left| {n + 1} \right\rangle_{\nu } \\ a_{\nu }^{ - } \left| n \right\rangle_{\nu } & = \sqrt n \left| {n - 1} \right\rangle_{\nu } . \\ \end{aligned}$$
(2)

Operator relations very similar to the classical optics relations (1) describe the coupling of the radiation channels: the creation operator relations are

$$\begin{aligned} a_{3}^{ + } & = \overline{R}a_{1}^{ + } + \overline{T}a_{2}^{ + } \\ a_{4}^{ + } & = \overline{T}a_{1}^{ + } + \overline{R}a_{2}^{ + } , \\ \end{aligned}$$
(3)

and the annihilation operator are given by the Hermitian conjugate equations. We also need the inverse relations:

$$\begin{aligned} a_{1}^{ + } & = Ra_{3}^{ + } + Ta_{4}^{ + } \\ a_{2}^{ + } & = Ta_{3}^{ + } + Ra_{4}^{ + } . \\ \end{aligned}$$
(4)

The coupling of the four radiation channels produced by the BS results in the exchange of a photon among them, e.g., a photon is destroyed in one channel, while some excitation is created in the others. We are, therefore, interested in states of our four-channel system with total energy corresponding to one photon. These states are linear combinations of the basis vectors formed by tensor products of states of the individual channels:

$$\begin{gathered} \left| {1000} \right\rangle = \left| 1 \right\rangle_{1} \left| 0 \right\rangle_{2} \left| 0 \right\rangle_{3} \left| 0 \right\rangle_{4} ;\quad \left| {0100} \right\rangle = \left| 0 \right\rangle_{1} \left| 1 \right\rangle_{2} \left| 0 \right\rangle_{3} \left| 0 \right\rangle_{4} ; \hfill \\ \left| {0010} \right\rangle = \left| 0 \right\rangle_{1} \left| 0 \right\rangle_{2} \left| 1 \right\rangle_{3} \left| 0 \right\rangle_{4} ;\quad \left| {0001} \right\rangle = \left| 0 \right\rangle_{1} \left| 0 \right\rangle_{2} \left| 0 \right\rangle_{3} \left| 1 \right\rangle_{4} . \hfill \\ \end{gathered}$$
(5)

For example, the vector \(\left| {0010} \right\rangle\) represents one photon in the output channel A3, while all other channels are empty. \(\left| {0000} \right\rangle = \left| 0 \right\rangle_{1} \left| 0 \right\rangle_{2} \left| 0 \right\rangle_{3} \left| 0 \right\rangle_{4}\) is the vacuum state. The set of state vectors (5) span the subspace on which the operators \(a_{\nu }^{ + } \,{\text{and}}\,a_{\nu }^{ - }\) act.

Let us now discuss output of the BS for a given input. To be specific, let initially one photon occupy channel A1:

$$\left| {{\text{In}}} \right\rangle = \left| {1000} \right\rangle .$$
(6)

This state can be generated by applying the creation operator \(a_{1}^{ + }\) on the vacuum state:

$$\left| {{\text{In}}} \right\rangle = a_{1}^{ + } \left| {0000} \right\rangle .$$
(7)

The final state is obtained by substituting for \(a_{1}^{ + }\) the corresponding relation from (4):

$$\left| {{\text{Fin}}} \right\rangle = (Ra_{3}^{ + } + Ta_{4}^{ + } )\left| {0000} \right\rangle .$$
(8)

Thus, the final state of the BS is given by

$$\left| {{\text{Fin}}} \right\rangle = R\left| {0010} \right\rangle + T\left| {0001} \right\rangle .$$
(9)

This is a very important result. The final state is a linear superposition of states from two different subsystems, A3 and A4. Such a combination of state vectors is called an entangled state. A remarkable property of the entanglement produced by the beam splitter is that we are unable to tell which output channel is occupied. As far as the delayed choice situation is concerned a basic misconception of some interpretations is the role of the BS and the idea that the photon must go one way or the other. Instead, the proper quantum treatment shows that an entangled state is produced and there is no answer to the question 'which way'.

How many photons are accumulated in output channel A3 and how many in A4 when the one-photon input experiment is repeated? The answer is given by the number of attempts times the quantum expectation values of the photon number operators \(N_{3}\) and \(N_{4}\):

$$\begin{aligned} n_{3} & = \left\langle {N_{3} } \right\rangle = \left\langle {a_{3}^{ + } a_{3}^{ - } } \right\rangle \\ n_{4} & = \left\langle {N_{4} } \right\rangle = \left\langle {a_{4}^{ + } a_{4}^{ - } } \right\rangle . \\ \end{aligned}$$
(10)

The expectation values of \(N_{3} \,{\text{and}}\,N_{4}\) for the final state are found as follows:

$$\begin{aligned} n_{3} & = \left\langle {{\text{Fin}}} \right|a_{3}^{ + } a_{3}^{ - } \left| {{\text{Fin}}} \right\rangle = \left\langle {0000} \right|(\overline{R}a_{3}^{ - } + \overline{T}a_{4}^{ - } )\,a_{3}^{ + } a_{3}^{ - } \,(Ra_{3}^{ + } + Ta_{4}^{ + } )\left| {0000} \right\rangle \\ n_{4} & = \left\langle {{\text{Fin}}} \right|a_{4}^{ + } a_{4}^{ - } \left| {{\text{Fin}}} \right\rangle = \left\langle {0000} \right|(\overline{R}a_{3}^{ - } + \overline{T}a_{4}^{ - } )\,a_{4}^{ + } a_{4}^{ - } (Ra_{3}^{ + } + Ta_{4}^{ + } )\left| {0000} \right\rangle \\ n_{3} & = \left| R \right|^{2} \\ n_{4} & = \left| T \right|^{2} . \\ \end{aligned}$$
(11)

As expected, the portion of photons received by the detector in the reflected and transmitted channel is given by the reflectivity \(\left| R \right|^{2}\) and the transmissivity \(\left| T \right|^{2}\), respectively. The result confirms energy conservation:

$$n_{3} + n_{4} = \left| R \right|^{2} + \,\,\left| T \right|^{2} \, = 1.$$
(12)

It is interesting to calculate expectation value \(\left\langle {N_{3} \,N_{4} } \right\rangle\) which represents the signal correlation of the two detectors. Making use of (10) it is readily verified that there is perfect anti-correlation of the detector response, \(\left\langle {N_{3} \,N_{4} } \right\rangle = 0\). When a photon is detected in channel A3, channel A4 is empty and vice versa.

3 The Mach–Zehnder interferometer

Let us now turn to the arrangement of Fig. 2, the Mach–Zehnder interferometer with channels B1 through B4. We are interested in the output of the second beam splitter, BS2. The input of BS2 is the entangled output of BS1, essentially given by (9). However, to allow for a phase shift between the input beams a factor \(e^{i\,\phi }\) is included:

$$\left| {{\text{In}}} \right\rangle_{{{\text{BS}}2}} = R\,\left| {1000} \right\rangle + e^{i\phi } \,T\,\left| {0100} \right\rangle = (R\,a_{1}^{ + } + e^{i\phi } \,T\,a_{2}^{ + } )\left| {0000} \right\rangle .$$
(13)

To get the final state we substitute for \(a_{1}^{ + } \,{\text{and}}\,a_{2}^{ + }\) using relation (4):

$$\begin{gathered} \left| {{\text{Fin}}} \right\rangle_{{{\text{BS}}2}} = \left[ {R(Ra_{3}^{ + } + Ta_{4}^{ + } ) + e^{i\phi } T(Ta_{3}^{ + } + Ra_{4}^{ + } )} \right]\left| {0000} \right\rangle \hfill \\ \left| {{\text{Fin}}} \right\rangle_{{{\text{BS}}2}} = (R^{2} + e^{i\phi } \,T^{2} )\left| {0010} \right\rangle + (1 + e^{i\phi } )\,R\,T\left| {0001} \right\rangle . \hfill \\ \end{gathered}$$
(14)

The final state of the MZI is also an entangled state, although slightly more complicated. One can convince oneself that all the manipulations have maintained the proper normalization of the calculated final state:

$$\left\langle {{\text{Fin}}} \right|\left. {{\text{Fin}}} \right\rangle_{{{\text{MIZ}}}} = \left\langle {{\text{Fin}}} \right|\left. {{\text{Fin}}} \right\rangle_{{{\text{BS}}2}} = (\left| R \right|^{2} + \,\,\left| T \right|^{2} )^{2} = 1.$$
(15)

The output characteristics of the MZI is given by the expectation values \(n_{3}\) and \(n_{4}\) of the corresponding photon number operators. The calculation runs very similar to the case of the simple BS, and the result is

$$\begin{aligned} n_{3} & = \left| {R^{2} + e^{i\,\phi } \,T^{2} } \right|^{2} \,\, \\ n_{4} & = \left| {R\,T(1 + e^{i\,\phi } )} \right|^{2} , \\ \end{aligned}$$
(16)

which can be written in a more convenient form as

$$\begin{aligned} n_{3} & = r^{4} + t^{4} - \,\,2\,r^{2} \,t^{2} \cos \phi \\ n_{4} & = 2\,r^{2} \,t^{2} + \,\,2\,r^{2} \,t^{2} \,\cos \phi \quad (R = r,\,\,T = i\,t). \\ \end{aligned}$$
(17)

Obviously, energy conservation is obeyed, \(n_{3} + n_{4} = 1\).

It is interesting to examine the special cases \(\phi = 0\) and \(\phi = \pi\). Let us take a fifty–fifty splitter, i.e., \(r = t = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}\).

For \(\phi\) = 0 the final state and the number of photons detected in channel B3 and B4 are

$$\left| {{\text{Fin}}} \right\rangle = i\,\,\left| {0001} \right\rangle$$
(18)
$$\begin{aligned} n_{3} & = 0 \\ n_{4} & = 1. \\ \end{aligned}$$
(19)

The final state is a simple state (no entanglement). Repeating the single photon experiment all photons are found in channel B4, while channel B3 is left empty.

For \(\phi\) = π, we have

$$\left| {{\text{Fin}}} \right\rangle = \left| {0010} \right\rangle$$
(20)
$$\begin{aligned} n_{3} & = 1 \\ n_{4} & = 0. \\ \end{aligned}$$
(21)

Now, all photons are found in channel B3 and no photons in B4.

The situations \(\phi = 0\,\,{\text{and }}\phi = \pi\) correspond to the case of constructive and destructive interference mentioned in the introduction. Only one detector receives signals, while the other sees nothing.

Letting \(\phi\) continuously vary we obtain an 'interference' pattern:

$$\begin{aligned} n_{3} & = \cos (\phi /2)^{2} \\ n_{4} & = \sin (\phi /2)^{2} . \\ \end{aligned}$$
(22)

For both output channels the numbers of detected photons vary sinusoidally, but in opposite sense. This is in exact agreement with the result of classical optics.

Note that in repeated single photon experiments identical patterns are produced no matter how much time passes between the events. An extremely slow succession will finally produce the same result when the total number of accumulated photons is the same.

4 Single photon wave packets

The simplified single mode quantum treatment employed so far is obviously not able to treat the temporal sequence of the interaction of the photon with the beam splitter. However, this aspect is essential in the discussion of the delayed choice experiment. Within the single mode framework all we can say is that a photon occupies a certain radiation mode, but it is not possible to indicate the time the photon enters the interferometer. It is thus impossible to specify whether the photon has passed the beam splitter before or after the positioning of the second beam splitter.

The temporal evolution can be readily included by forming photon wave packets. Here we are interested in wave packets representing n-photon number states (Fock states), i.e., Eigenstates of the photon number operator [12, 14].

The wave packet creation operators are constructed by superposition of time-dependent continuous mode operators \(a_{\nu }^{ + } (t)\). The subscript ν indicates the radiation mode.

The state vector representing a 1-photon wave packet in channel \(\nu\) can be written:

$$\left| 1 \right\rangle_{\nu }^{t} = \,\,\int {{\text{d}}t^{\prime}V(t^{\prime} - t)} \,\,a_{\nu }^{ + } (t^{\prime})\left| 0 \right\rangle \quad \left( {\int {\left| {V(t^{\prime})} \right|}^{2} {\text{d}}t^{\prime} = 1} \right),$$
(23)

where \(V(t^{\prime} - t)\) is the complex amplitude of a wave packet peaked at time \(t\), \(a_{v}^{ + } (t^{\prime})\) is the operator creating a photon at time \(t^{\prime}\) and \(\left| 0 \right\rangle\) is the appropriate vacuum state. The complex amplitude function \(V(t)\) is determined by the properties of the photon source.

The wave packet (23) is probably the best possible description that quantum physics can offer for the naïve picture of a single photon propagating along a trajectory. As a matter of fact, the wave packet description insures compliance with the uncertainty relation.

Let us skip the application of the wave packet concept to a simple beam splitter and instead consider directly the MZI, namely, the example of one photon incident in channel A1.

To calculate the output the appropriate time dependent input/output channel coupling relation equivalent to (4) are required. The mathematical derivation is somewhat laborious and is omitted here. The outcome given below agrees with the intuitive result that may be obtained from an inspection of Fig. 2:

$$a_{1}^{ + } (t) = R^{2} a_{3}^{ + } (t) + T^{2} a_{3}^{ + } (t - \tau ) + R\,\,T(a_{4}^{ + } (t) + a_{4}^{ + } (t - \tau )).$$
(24)

The delay time τ can be produced by suitably controlling the optical path length of the interferometer arms.

The output state is a superposition of four wave packet states:

$$\left| {{\text{Fin}}} \right\rangle = R^{2} \left| 1 \right\rangle_{3}^{t} + T^{2} \left| 1 \right\rangle_{3}^{t - \tau } + R\,T\left( {\left| 1 \right\rangle_{4}^{t} + \left| 1 \right\rangle_{4}^{t - \tau } } \right).$$
(25)

\(\left| 1 \right\rangle_{3}^{t}\) and \(\left| 1 \right\rangle_{3}^{t - \tau }\) represent one-photon wave packets in output channel B3 peaked at time \(t\) and \(t - \tau\), respectively, and \(\left| 1 \right\rangle_{4}^{t}\) and \(\left| 1 \right\rangle_{4}^{t - \tau }\) are the corresponding wave packets in channel B4.

Finally, let us discuss the expectation values of the photon numbers \(n_{3} (t)\) and \(n_{4} (t)\) for the final state \(\left| {{\text{Fin}}} \right\rangle\):

$$\begin{aligned} n_{3} (t) & = \left\langle {a_{3}^{ + } (t)\,a_{3}^{ - } (t)} \right\rangle = \left\langle {{\text{Fin}}} \right|a_{3}^{ + } (t)\,a_{3}^{ - } (t)\left| {{\text{Fin}}} \right\rangle \\ n_{4} (t) & = \left\langle {a_{4}^{ + } (t)\,a_{4}^{ - } (t)} \right\rangle = \left\langle {{\text{Fin}}} \right|a_{4}^{ + } (t)\,a_{4}^{ - } (t)\left| {{\text{Fin}}} \right\rangle . \\ \end{aligned}$$
(26)

Using (25) and the definition of the wave packet states (24) we obtain

$$\begin{aligned} n_{3} (t) & = \left| {R^{2} V(t) + T^{2} V(t - \tau )} \right|^{2} \\ n_{4} (t) & = \left| R \right|^{2} \left| T \right|^{2} \left| {V(t) + V(t - \tau )} \right|^{2} . \\ \end{aligned}$$
(27)

The similarity with the corresponding single mode relations (16) is quite apparent.

Let us take a closer look at the result (27). With no extra phase shift in A2 (ϕ = 0) we have \(\tau = 0\) and obtain:

$$\begin{aligned} n_{3} (t) & = \left| {R^{2} + T^{2} } \right|^{2} \left| {V(t)} \right|^{2} \\ n_{4} (t) & = 4\left| R \right|^{2} \left| T \right|^{2} \left| {V(t)} \right|^{2} . \\ \end{aligned}$$
(28)

In the delayed choice experiment identical 50:50 mirrors are considered. In this case we have complete destructive and constructive interference and Eq. (28) reduce to

$$\begin{aligned} n_{3} (t) & = 0 \\ n_{4} (t) & = \left| {V(t)} \right|^{2} . \\ \end{aligned}$$
(29)

Bearing in mind \(\int {\left| {V(t^{\prime})} \right|}^{2} {\text{d}}t^{\prime} = 1\) this result shows that the input photon wave packet ends up for sure in channel B4 and thus on detector D2. No photons arrive on D1. The result for this case could be directly inferred from (25) which gives \(\left| {{\text{Fin}}} \right\rangle = \left| 1 \right\rangle_{4}^{t}\). The final state is not entangled.

The situation discussed in the preceding paragraph is the scenario encountered in the original delayed choice experiment. For interference to occur, it is obviously irrelevant at what time the photon wave packet reaches the first beam splitter BS1. The significant condition for interference is that the second beam splitter is in position before leading edge of the wave packet arrives.

The final point of interest is the situation when the time between the wave packets is much greater than their duration [15] and there is no temporal overlap. Integration of Eq. (25) yields

$$\begin{aligned} \int {n_{3} } (t^{\prime}){\text{d}}t^{\prime} & = \left| R \right|^{4} + \left| T \right|^{4} = \frac{1}{2} \\ \int {n_{4} } (t^{\prime}){\text{d}}t^{\prime} & = 2\left| R \right|^{2} \left| T \right|^{2} = \frac{1}{2} \\ \end{aligned}$$
(30)

Thus, if the delay time between the wave packets introduced in the interferometer is very large, the MZI works just like an ordinary beam splitter. The detectors D1 and D2 are randomly activated with equal probability of 50%.

5 Conclusions

The incentive to write this article was the ongoing discussion of the delayed choice experiment and its role as an illustration of the wave-particle duality of quantum physics [7]. Some of the explanation that can be found not only on popular channels but also in the literature and in textbooks suffer from inconsistent concepts, typically mixing classical and quantum physics ones. Here I have tried to remind the reader of the strictly quantum optical approach [12] that leaves no mystery except of cause the intrinsic mystery of quantum physics itself [16].

I started by discussing the case of single-photon input onto a simple optical beam splitter. It has been pointed out that a unique quantum physics process occurs, namely, the formation of an entangled state. As a matter of principle, for the entangled state the photon cannot be assigned to the reflected or the transmitted beam. Accordingly, there is no choice to be made and the question 'which way' the particle goes cannot be answered. As a matter of fact, as far as the nature of photons is concerned, the notions 'particle’ and ‘wave' do not appear in the quantum optics description used here. According to this view a photon is just a quantum of energy contained or exchanged in or between quantum systems (see, e.g., p. 1 in [12]).

The simplified single mode quantum treatment has been used to describe the basic quantum interactions in the beam splitter and the Mach–Zehnder interferometer. The extension of the single mode model to the wave packet concept enabled the treatment of the temporal aspects which play an essential role in the discussion of the delayed choice issue.

In the light of entanglement and of the Fock state wave packet description of a single photon, the delayed introduction of a second BS simply means that after the contact with the first BS, one more interaction will occur if the photon wave packet on its way meets a second BS. It does not matter if this one is in position before or after the contact of the photon with the first BS. It only matters that the second BS is there before the leading edge of the photon wave packet arrives.

The more elaborate wave packet treatment provided deeper insight into the photon interactions, but did not change the basic conclusions of the single-mode approach.