Unambiguous atomic Bell measurement assisted by multiphoton states

Abstract

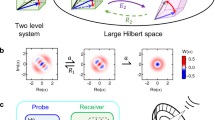
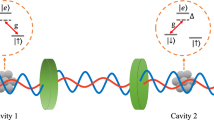
We propose and theoretically investigate an unambiguous Bell measurement of atomic qubits assisted by multiphoton states. The atoms interact resonantly with the electromagnetic field inside two spatially separated optical cavities in a Ramsey-type interaction sequence. The qubit states are postselected by measuring the photonic states inside the resonators. We show that if one is able to project the photonic field onto two coherent states on opposite sites of phase space, an unambiguous Bell measurement can be implemented. Thus, our proposal may provide a core element for future components of quantum information technology such as a quantum repeater based on coherent multiphoton states, atomic qubits and matter–field interaction.

Appendices

Appendix 1: Approximations with large mean photon numbers

In this Appendix, we present the derivation of the time-dependent state vector of Eq. (9). It has been shown in Ref. [25, 40] that the time evolution of any initial state in the form of Eq. (3) can be obtained from the solution of the eigenvalue problem of the two-atom Tavis–Cummings Hamiltonian (1). The exact solution can be written in the following form

$$\begin{aligned} | {{\varPsi }_t} \rangle =& | {0,0} \rangle | {\chi _t^0} \rangle +| {1,1} \rangle | {\chi ^{1}_t} \rangle \nonumber\\&+| {{\varPsi }^+} \rangle | {\chi ^+_t} \rangle +c_-| {{\varPsi }^-} \rangle | {\alpha } \rangle \end{aligned}$$

(20)

with the relevant photonic states

$$\begin{aligned} | {\chi ^0_t} \rangle&= c_0\,p_0| {0} \rangle + \sum _{n=1}^\infty \tfrac{ \sqrt{n} \left( \xi _{n,t}^- -\xi _{n,t}^+\right) +\sqrt{n-1}\xi _{n} }{\sqrt{2n-1}} | {n} \rangle , \nonumber \\ | {\chi ^1_t} \rangle&=\sum _{n=2}^\infty \tfrac{ \sqrt{n-1} \left( \xi _{n,t}^- -\xi _{n,t}^+\right) -\sqrt{n}\xi _{n} }{\sqrt{2n-1}} | {n-2} \rangle , \nonumber \\ | {\chi ^+_t} \rangle&= \sum _{n=1}^\infty \left( \xi _{n,t}^-+\xi _{n,t}^+ \right) | {n-1} \rangle , \end{aligned}$$

(21)

and with the aid of the following abbreviations

$$\begin{aligned}&\xi _{n,t}^\pm = \frac{e^{\pm i \omega _n t}}{2} \left( c_+p_{n-1}\mp \tfrac{\sqrt{n}\,c_0 p_n+\sqrt{n-1}\,c_1 p_{n-2}}{\sqrt{2n-1}} \right) , \nonumber \\&\xi _{n} = \frac{\sqrt{n-1}\,c_0 p_n-\sqrt{n}\,c_1 p_{n-2}}{\sqrt{2n-1}},\quad \omega _n=g\sqrt{4n-2}. \nonumber \end{aligned}$$

The coefficients $p_n$ are initial probability amplitudes of the photon number states $| {n} \rangle$ of the initial field state $| {\alpha } \rangle$. The coefficients $c_0$ and $c_1$ are the initial probability amplitudes of the states $| {0,0} \rangle$ and $| {1,1} \rangle$ and are related to the probability amplitudes of the state in Eq. (3) by

$$\begin{aligned} d_\phi ^\pm&= \frac{c_0 e^{i\phi }\pm c_1 e^{-i\phi }}{\sqrt{2}}. \end{aligned}$$

(22)

The expressions of Eq. (21) can be significantly simplified approximately by taking into account that the field is initially prepared in a coherent state $| {\alpha } \rangle$ with photonic distribution $p_n=\exp (-\bar{n}/2+i\phi )\sqrt{\bar{n}^{n}/n!}$ and by assuming a large mean photon number $\bar{n}=|\alpha |^2\gg 1$. In such case, the photonic distribution has the following property

$$\begin{aligned} p_n=\sqrt{\frac{\bar{n}}{n}}e^{i\phi }p_{n-1}\approx e^{i\phi }p_{n-1}. \end{aligned}$$

(23)

Applying this approximation to the states of Eq. (21), we find the following approximations

$$\begin{aligned}&| {\chi ^0_t} \rangle \approx \sum _{n=1}^\infty \tfrac{ ({c_+}\,+\,d_\phi ^+) e^{-i\omega _n t} -({c_+}\,-\,d_\phi ^+) e^{i\omega _n t} \,+\,2d_\phi ^- }{2\sqrt{2}} p_{n-1} | {n} \rangle , \nonumber \\&| {\chi ^1_t} \rangle \approx \sum _{n=2}^\infty \tfrac{ ({c_+}\,+\,d_\phi ^+) e^{-i\omega _n t} \,-\,({c_+}\,-\,d_\phi ^+) e^{i\omega _n t} \,-\,2d_\phi ^- }{2\sqrt{2}} {p_{n-1}} | {n-2} \rangle , \nonumber \\&| {\chi ^+_t} \rangle \approx \sum _{n=1}^\infty \tfrac{ (c_++d_\phi ^+) e^{-i\omega _n t} +({c_+}\,-\,d_\phi ^+) e^{i\omega _n t} }{2} p_{n-1} | {n-1} \rangle . \nonumber \end{aligned}$$

In order to simplify these expressions, we perform a Taylor expansion in the frequencies $\omega _n$ around $\bar{n}+1$ as

$$\begin{aligned} \omega _n/g&\approx \sqrt{4 \bar{n}+2}+2\frac{n-\bar{n}-1}{\sqrt{4\bar{n}+2}} -2\frac{(n-\bar{n}-1)^2}{(4\bar{n}+2)^{3/2}}. \end{aligned}$$

(24)

The previous second-order expansion is valid provided the third-order contribution multiplied by gt is negligible. This imposes the restriction on the interaction time

$$\begin{aligned} t\ll \frac{(4\bar{n}+2)^{5/2}}{4g \bar{n}^{3/2}} \approx \bar{n}/g. \end{aligned}$$

(25)

For the rescaled time $\tau =gt/\pi \sqrt{4\bar{n} +2}$ used in the main text this implies $\tau \ll \sqrt{\bar{n}}/2\pi$. In this approximation, the field states can be written as

$$\begin{aligned} | {\chi ^0_t} \rangle&\approx e^{-i\phi } \tfrac{ (c_++d_\phi ^+) | {\alpha _t^{-},-1} \rangle -(c_+-d_\phi ^+) | {\alpha _t^{+},-1} \rangle +2d_\phi ^-| {\alpha } \rangle }{2\sqrt{2}}, \nonumber \\ | {\chi ^1_t} \rangle&\approx e^{i\phi } \tfrac{ (c_++d_\phi ^+) | {\alpha _t^{-},1} \rangle -(c_+-d_\phi ^+) | {\alpha _t^{+},1} \rangle -2d_\phi ^-| {\alpha } \rangle }{2\sqrt{2}}, \nonumber \\ | {\chi ^+_t} \rangle&\approx \tfrac{ (c_++d_\phi ^+) | {\alpha ^{-}_t,0} \rangle +(c_+-d_\phi ^+) | {\alpha ^{+}_t,0} \rangle }{2}, \end{aligned}$$

(26)

with

$$\begin{aligned} | {\alpha _t^\pm ,j} \rangle&= \sum _{n=0}^\infty e^{-\frac{|\alpha |^2}{2}}\frac{\alpha ^n}{\sqrt{n!}} e^{\pm i \left( \nu +2\tfrac{n-\bar{n}+j}{\nu }-2\frac{(n-\bar{n}+j)^2}{\nu ^3} \right) g t} | {n} \rangle \nonumber \\&\approx e^{\pm ij2\pi \tau }| {\alpha ^\pm _\tau } \rangle , \end{aligned}$$

(27)

$j\in \{-1,0,1\}$ and $\nu =\sqrt{4\bar{n} +2}$. Furthermore, the states $| {\alpha _\tau ^\pm } \rangle$ are defined by Eq. (10). We neglected the contribution of j in the quadratic term of the exponent in Eq. (27). This can be justified given the fact a Poisson distribution with high mean value is almost symmetrically centered around its mean with variance equal to its mean. This implies that the maximal relevant value in the quadratic term is given by

$$\begin{aligned} \mathrm{max}\left\{ \frac{(n-\bar{n}+j)^2}{\nu }\right\} \approx 2+\frac{2j}{\sqrt{\bar{n}}}+\frac{j}{2\bar{n}}, \end{aligned}$$

which shows that the contribution of $j=-1,0,1$ to this term is negligible for $\bar{n}\gg 1$.

Finally, using the approximations of Eq. (26) and (27) in Eq. (20) and separating the atomic states accompanying to the photonic states $| {\alpha _\tau ^\pm } \rangle$ and $| {\alpha } \rangle$ yields the result of Eq. (9).

Appendix 2: Evaluation of $\langle {\alpha }|{\alpha ^\pm _\tau }\rangle$ and $\langle {-\alpha }|{\alpha ^\pm _\tau }\rangle$

Fig. 6

Top (bottom) figure: real part of the overlap $\langle {\alpha }|{\alpha ^+_\tau }\rangle$ ($\langle {-\alpha }|{\alpha ^+_\tau }\rangle$) as function of the rescaled time $\tau$. The red curve was evaluated using the exact expression in the first line of Eq. (28) and the black narrow line corresponds to the approximation given in Eq. (29). The mean photon number is $\bar{n}=12.16$

In this appendix, we investigate the overlaps between the field states $| {\alpha ^\pm _\tau } \rangle$ and $| {\pm \alpha } \rangle$ defined in Eqs. (10) and (4), respectively. Using the index $j\in \{-1,1\}$ one can write a single expression for the four overlaps as

$$\begin{aligned} \langle {j\alpha }|{\alpha _{\tau }^\pm }\rangle&= \sum _{n=0}^{\infty } \frac{\bar{n}^{n}j^n}{n!e^{\bar{n}}} e^{ \pm i 2\pi \tau \left[ \bar{n}\,+\,1\,+\,n -\frac{(n-\bar{n})^2}{4\bar{n}+2}\right] }\nonumber \\&\approx \frac{ e^{\pm i(\bar{n} +1)2\pi \tau } }{\sqrt{2\pi \bar{n}}} \sum _{n=-\infty }^\infty e^{ \pm i \pi n\left( 2\tau \,+\,\frac{1-j}{2}\right) -\frac{(1\,\pm\, i\pi \tau )}{2\bar{n}}(n\,-\,\bar{n})^2} \nonumber \\&= \frac{ e^{\pm i(\bar{n} \,+\,1)2\pi \tau } }{\sqrt{1\pm i\pi \tau }} \sum _{n=-\infty }^\infty e^{ \pm i2\pi \bar{n}\left( \tau +\frac{1-j}{4}\pm n\right) -\frac{2\pi ^2 \bar{n}}{1\pm i\pi \tau }\left( \tau +\frac{j-1}{4}\pm n\right) ^2 }. \end{aligned}$$

(28)

In the second line, we have approximated the Poisson distribution by a normal distribution and we have extended the sum to $-\infty$. These approximations are valid in the limit $\bar{n}\gg 1$. In the third line, we have used the Poisson summation formula [47] which in the case of a Gaussian sum can be expressed as

$$\begin{aligned} \sum _{n=-\infty }^\infty e^{i2\pi un-s (n-\bar{n})^2}= \sqrt{\frac{\pi }{s}}\sum _{n=-\infty }^\infty e^{i2\pi \bar{n}(n+u) -\frac{\pi ^2}{s}(n+u)^2}, \nonumber \end{aligned}$$

with $\mathrm{Re}[s]>0$. The last expression in Eq. (28) involves a summation of Gaussian terms with variance $(1+\pi ^2\tau ^2)/4\pi ^2\bar{n}$. This variance is very small provided the condition $4\bar{n}\gg \tau ^2$ is fulfilled. If this requirement is met, there exists a dominant contribution in the summation that corresponds to the value of n where $|\tau +(1-j)/4\pm n|$ achieves its minimum value. This minimum can be evaluated as

$$\begin{aligned} f_j(\tau )= \mathrm{frac}\left( \tau +\tfrac{1\,-\,j}{4}+\tfrac{1}{2}\right) -\tfrac{1}{2}, \end{aligned}$$

where $\mathrm{frac}(x)$ denotes the fractional part of x. By considering only the dominant term of the last summation in Eq. (28), one can find the following approximation of the overlap between field states

$$\begin{aligned} \langle {j\alpha }|{\alpha ^\pm _{\tau }}\rangle&\approx \frac{ e^{\pm i2\pi [\bar{n} f_j(\tau )\,+\,(\bar{n} +1)\tau ]} }{\sqrt{1\pm i\pi \tau }} e^{-\frac{2\pi ^2 \bar{n}}{1\pm i\pi \tau }[f_j(\tau )]^2}, \end{aligned}$$

(29)

with $j\in \{-1,1\}$. This result for $\tau =1/2$ and $j=-1$ has been rewritten in polar form in Eq. (14) of the main text, where we used that $f_{-1}(1/2)=0$. In Eq. (13) we have used that $f_1(1/2)=-1/2$. In the top panel of Fig. 6 we have plotted the real part of the overlap $\langle {\alpha }|{\alpha ^+_\tau }\rangle$ as a function of the rescaled time $\tau$. The evaluation of the exact expression is shown in red and the approximation in black. The collapse and revival phenomena are well described by the approximation of the overlap in Eq. (29). Similar treatment to describe the collapse and revival phenomena in the Jaynes–Cummings model has been presented in Ref. [48]. In the bottom figure of Fig. 6, we have plotted the real part of the overlap $\langle {-\alpha }|{\alpha ^+_\tau }\rangle$ .