Far-Field Expansions for Harmonic Maps and the Electrostatics Analogy in Nematic Suspensions

Abstract

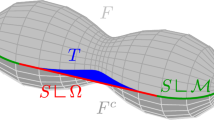
For a smooth bounded domain $G\subset {{\mathbb {R}}}^3$, we consider maps $n:{\mathbb {R}}^3\setminus G\rightarrow {\mathbb {S}}^2$ minimizing the energy $E(n)=\int _{{\mathbb {R}}^3{\setminus } G}|\nabla n|^2 +F_s(n_{\lfloor \partial G})$ among ${\mathbb {S}}^2$-valued map such that $n(x)\approx n_0$ as $|x|\rightarrow \infty$. This is a model for a particle G immersed in nematic liquid crystal. The surface energy $F_s$ describes the anchoring properties of the particle and can be quite general. We prove that such minimizing map n has an asymptotic expansion in powers of 1/r. Further, we show that the leading order 1/r term is uniquely determined by the far-field condition $n_0$ for almost all $n_0\in {\mathbb {S}}^2$, by relating it to the gradient of the minimal energy with respect to $n_0$. We derive various consequences of this relation in physically motivated situations: when the orientation of the particle G is stable relative to a prescribed far-field alignment $n_0$; and when the particle G has some rotational symmetries. In particular, these corollaries justify some approximations that can be found in the physics literature to describe nematic suspensions via a so-called electrostatics analogy.

Appendix A: Decay Estimates for Poisson’s Equation

We collect here some folklore decay estimates for Poisson’s equation. For the reader’s convenience, we include a self-contained proof (similar arguments can be found, e.g. in (Pacard and Rivière 2000, § 2.2.3) for Hölder decay at the origin). The elementary arguments we present here do not seem to apply directly for general systems as in Remark 1, in that case one should refer to (Bella et al. 2020, § 5-6).

Lemma A.1

Let $d\ge 3$, $\gamma >d-2$, $\gamma \notin {\mathbb {N}}$, and f a function in ${{\mathbb {R}}}^d\setminus B_1$ satisfying

$$\begin{aligned} |f(x)|\le \frac{1}{r^{\gamma +2}}\qquad \text {for }r=|x|\ge 1. \end{aligned}$$

Then, there exists a function u such that $\Delta u =f$ in ${{\mathbb {R}}}^d\setminus B_1$ and

$$\begin{aligned} \frac{|u(x)|}{r} +|\nabla u(x)|\lesssim \frac{1}{r^{\gamma +1}}, \end{aligned}$$

(A.1)

where the constant depends only on d and $\gamma$.

Note that (A.1) does not determine u uniquely, as we may add any faster-decaying harmonic terms to u without changing the equation $\Delta u=f$, but the proof does determine an explicit right inverse $f\mapsto u$ to the Laplacian in that decay range.

We will obtain Lemma A.1 as a consequence of an $L^2$ version of it, that we state now.

Lemma A.2

Let $d\ge 3$, $\gamma >d-2$, $\gamma \notin {\mathbb {N}}$, and f a function in ${{\mathbb {R}}}^d\setminus B_1$ satisfying

$$\begin{aligned} \left( \frac{1}{R^d}\int _{{\vert x\vert }> R} {\vert x\vert }^2 f^2 \, dx \right) ^{\frac{1}{2}}&\le \frac{1}{R^{\gamma +1}}\qquad \forall R\ge 1, \end{aligned}$$

(A.2)

Then, there exists a function u such that $\Delta u =f$ in ${{\mathbb {R}}}^d\setminus B_1$ and

$$\begin{aligned} \left( \frac{1}{R^d}\int _{{\vert x\vert }\ge R}\frac{{\vert u\vert }^2}{|x|^2}\, dx\right) ^{\frac{1}{2}}&\lesssim \frac{1}{R^{\gamma +1}}\qquad \forall R\ge 1, \end{aligned}$$

(A.3)

where the implicit constant depends only on d and $\gamma$.

Before proving Lemma A.2, we explain why, together with rescaled elliptic estimates, it implies Lemma A.1.

Proof of Lemma A.1

The assumption on f implies that it satisfies the $L^2$ decay in the assumption of Lemma A.2, so we obtain u such that $\Delta u=f$ in ${{\mathbb {R}}}^d\setminus B_1$ and

$$\begin{aligned} \left( \frac{1}{R^d}\int _{{\vert x\vert }\ge R}\frac{{\vert u\vert }^2}{|x|^2}\, dx\right) ^{\frac{1}{2}} \lesssim \frac{1}{R^{\gamma +1}}\qquad \forall R\ge 1, \end{aligned}$$

and the pointwise bound (A.1) in the conclusion of Lemma A.1 follows from rescaled elliptic estimates. Explicitly, consider ${\hat{u}}({\hat{x}})=u(R{\hat{x}})$ which solves $\Delta {\hat{u}} = {\hat{f}}$, where ${\hat{f}}({\hat{x}}):=R^2 f(R{\hat{x}})$, then from interior elliptic estimates (see, e.g. Gilbarg and Trudinger (2001)) we have

$$\begin{aligned} \sup _{B_3\setminus B_2}\left( |{\hat{u}}| + |\nabla {\hat{u}}| \right)&\lesssim \left( \int _{B_4\setminus B_1}|{\hat{u}}|^2 \right) ^{\frac{1}{2}} + \sup _{B_4\setminus B_1}|{\hat{f}}|\\&\lesssim R \left( \frac{1}{R^d}\int _{|x|\ge R}\frac{|u|^2}{|x|^2} \right) ^{\frac{1}{2}}+\frac{1}{R^{\gamma }}, \end{aligned}$$

from which, scaling back, we infer (A.1).

Next, we prove Lemma A.2. Before doing so, we recall some facts concerning spherical harmonics (that is, homogeneous harmonic polynomials), referring the reader to Stein and Weiss (1971) for details. The Laplace–Beltrami operator on ${\mathbb {S}}^{d-1}$ diagonalizes as

$$\begin{aligned} -\Delta _{{\mathbb {S}}^{d-1}}\Phi _j =\lambda _j \Phi _j,\qquad 0= \lambda _0 \le \lambda _1\le \cdots \end{aligned}$$

The set $\lbrace \lambda _j\rbrace _{j\in {\mathbb {N}}}$ coincides with $\lbrace k^2 + k(d-2)\rbrace _{k\in {\mathbb {N}}}$. The eigenfunctions corresponding to $k^2 + k(d-2)$ span the homogeneous harmonic polynomials of degree k. We choose them normalized in $L^2(\mathbb S^{d-1})$ so they form an orthonormal Hilbert basis of this space. For a $W^{2,2}_{loc}$ function $w:(0,\infty ) \rightarrow \mathbb {R}$, we have

$$\begin{aligned} \Delta (w(r)\Phi _j(\omega )) =({\mathcal {L}}_j w )(r) \Phi _j(\omega ),\qquad {\mathcal {L}}_j =\partial _{rr} +\frac{d-1}{r}\partial _r -\frac{\lambda _j}{r^2}. \end{aligned}$$

(A.4)

The solutions of ${\mathcal {L}}_j w=0$ are linear combinations of $r^{\gamma _j^+}$ and $r^{-\gamma _j^-}$, where $\gamma _j^\pm \ge 0$ are given by

$$\begin{aligned} \gamma _j^+&= \sqrt{\left( \frac{d-2}{2}\right) ^2 +\lambda _j} - \frac{d-2}{2} = k \qquad&\text {for }\lambda _j =k^2+k(d-2),\\ \gamma _j^-&= \sqrt{\left( \frac{d-2}{2}\right) ^2 +\lambda _j} + \frac{d-2}{2} = k +d-2 \qquad&\text {for }\lambda _j =k^2+k(d-2). \end{aligned}$$

The decay rate $\gamma >d-2$, $\gamma \notin {\mathbb {N}}$, is fixed, and we denote by $j_0=j_0(\gamma )$ the integer $j_0\ge 0$ such that

$$\begin{aligned}&\left\{ j\in {\mathbb {N}} :\gamma _j^- <\gamma \right\} =\lbrace 0,\ldots , j_0\rbrace ,\\&\left\{ j\in {\mathbb {N}} :\gamma _j^- > \gamma \right\} =\lbrace j_0 + 1, j_0 +2,\ldots \rbrace . \end{aligned}$$

Proof of Lemma A.2

We extend f to be defined in ${{\mathbb {R}}}^d$, with the property that

$$\begin{aligned} \left( \int _{{\vert x\vert }\le 1} {\vert x\vert }^2f^2 \, dx\right) ^{\frac{1}{2}}&\le 1 \end{aligned}$$

and will construct a function u such that $\Delta u=f$ in ${{\mathbb {R}}}^d\setminus \lbrace 0\rbrace$. The function $f\in L^2({{\mathbb {R}}}^d)$ admits a spherical harmonics expansion

$$\begin{aligned} f =\sum _{j\ge 0} f_j(r)\Phi _j(\omega ), \end{aligned}$$

and the decay assumption (A.2) on f amounts to

$$\begin{aligned} \sum _{j\ge 0}\int _R^\infty f_j(r)^2r^{d+1}\, dr \le R^{d-2\gamma -2}. \end{aligned}$$

(A.5)

We define u as

$$\begin{aligned} u:=\sum _{j\ge 0} u_j(r)\Phi _j(\omega ), \end{aligned}$$

where $u_j\in W^{2,2}_{loc}(0,\infty )$ satisfy

$$\begin{aligned} {\mathcal {L}}_j u_j =f_j. \end{aligned}$$

To write down an explicit formula for $u_j$, we rewrite $\mathcal L_j$, defined in (A.4), as

$$\begin{aligned} {\mathcal {L}}_j u =r^{-d+1+\gamma _j^-}\partial _r [ r^{d-1-2\gamma _j^-} \partial _r ( r^{\gamma _j^-}u) ], \end{aligned}$$

and define

$$\begin{aligned} u_j(r)&= \left\{ \begin{aligned} r^{-\gamma _j^-}\int _r^\infty t^{2\gamma _j^-+1-d}\int _t^\infty s^{d-1-\gamma _j^-} f_j(s)\, ds\, dt&\qquad \text {if }j\in \lbrace 0,\ldots , j_0\rbrace ,\\ r^{-\gamma _j^-}\int _0^r t^{2\gamma _j^-+1-d}\int _t^\infty s^{d-1-\gamma _j^-} f_j(s)\, ds \, dt&\qquad \text {if }j \ge j_0 +1. \end{aligned} \right. \end{aligned}$$

(A.6)

This is well defined because for any $t >0$ using Cauchy–Schwarz, (A.5) with the choice $R = t$, and the fact that $\gamma _j^-\ge d-2>0$, we can estimate the inner integral by

$$\begin{aligned} \int _t^\infty s^{d-1-\gamma _j^-} {\vert f_j(s)\vert }\, ds&\le \left( \int _t^\infty s^{-2-2\gamma _j^-}s^{d-1}ds\right) ^{\frac{1}{2}} \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) ^{\frac{1}{2}} \nonumber \\&\leqslant \frac{1}{\sqrt{2\gamma _j^- + 2-d}}t^{\tfrac{d}{2} - \gamma _j^- - 1} t^{\tfrac{d}{2} - \gamma - 1} \nonumber \\&= \frac{1}{\sqrt{ 2\gamma _j^- + 2-d}} t^{d - \gamma - \gamma _j^- -2} . \end{aligned}$$

(A.7)

Furthermore, as $t\mapsto t^{2\gamma _j^- + 1 - d }t^{d-2-\gamma - \gamma _j^-} = t^{\gamma _j^--\gamma -1}$ is integrable near $\infty$ if $\gamma _j^-<\gamma$, i.e. if $j\le j_0$; and is integrable near 0 if $\gamma _j^->\gamma$, i.e. if $j\ge j_0 +1$, the functions $u_j$ in (A.6) are well-defined.

Let $j\le j_0$ and set

$$\begin{aligned} \alpha {:}{=}\gamma +\gamma _{j_0}^- +1 -d, \end{aligned}$$

so that $2\gamma +1 - d>\alpha > 2\gamma _j^-+1 - d$. By (A.7) and Cauchy–Schwarz, we have

$$\begin{aligned} |u_j(r)|^2&\le \frac{r^{-2\gamma _j^-}}{2+2\gamma _j^--d}\left( \int _r^\infty t^{\gamma _j^--\frac{d}{2}} \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) ^{\frac{1}{2}}\, dt \right) ^2 \\&= \frac{r^{-2\gamma _j^-}}{2+2\gamma _j^--d}\left( \int _r^\infty t^{\gamma _j^--\frac{d}{2}-\frac{\alpha }{2}} t^{\frac{\alpha }{2}}\left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) ^{\frac{1}{2}}\, dt \right) ^2 \\&\le \frac{r^{-2\gamma _j^-}}{2+2\gamma _j^--d} \int _r^\infty t^{2\gamma _j^--d-\alpha }\, dt \int _r^{\infty }t^{\alpha } \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) \, dt \\&= \frac{r^{-d+1-\alpha }}{(2+2\gamma _j^--d)(\alpha -2\gamma _j^- +d - 1)} \int _r^{\infty }t^{\alpha } \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) \, dt\\&\le \frac{r^{-d+1-\alpha }}{(d-2)(\gamma -\gamma _{j_0}^-)} \int _r^{\infty }t^{\alpha } \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) \, dt, \end{aligned}$$

where in the last line, we used that $\gamma _j^- \geqslant d-2$ so that $2 + 2\gamma _j^- - d \geqslant d-2,$ and that $\gamma + \gamma _{j_0}^- - 2\gamma _{j}^- \geqslant \gamma - \gamma _{j_0}^-,$ when $j \leqslant j_0.$ Summing and using (A.5), we deduce

$$\begin{aligned} \sum _{j=0}^{j_0} \frac{|u_j(r)|^2}{r^2}&\le \frac{r^{-d-1-\alpha }}{(d-2)(\gamma -\gamma _{j_0}^-)} \int _r^{\infty }t^{\alpha } \left( \sum _{j=0}^{j_0}\int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) \, dt \\&\le \frac{r^{-d-1-\alpha }}{(d-2)(\gamma -\gamma _{j_0}^-)} \int _r^{\infty }t^{\alpha +d-2\gamma -2}\, dt \\&=\frac{r^{-2\gamma -2}}{(d-2)(\gamma -\gamma _{j_0}^-)(2\gamma +1 -d -\alpha )}\\&\le \frac{r^{-2\gamma -2}}{(d-2)(\gamma -\gamma _{j_0}^-)^2}. \end{aligned}$$

Similarly, for $j\ge j_0+1$ we set

$$\begin{aligned} \beta = \gamma +\gamma _{j_0+1}^- +1 -d, \end{aligned}$$

which satisfies $2\gamma +1 - d<\beta < 2\gamma _j^-+1 - d$. Using (A.7) and Cauchy–Schwarz, we find

$$\begin{aligned} |u_j(r)|^2&\le \frac{r^{-d+1-\beta }}{(d-2)(\gamma _{j_0+1}^- -\gamma )} \int _0^{r}t^{\alpha _j} \left( \int _t^\infty s^2f_j(s)^2s^{d-1}ds\right) \, dt, \end{aligned}$$

so that, we similarly obtain from (A.5) that

$$\begin{aligned} \sum _{j=j_0+1}^{\infty } \frac{|u_j(r)|^2}{r^2}&\le \frac{r^{-2\gamma -2}}{(d-2)(\gamma _{j_0+1}^- -\gamma )^2}. \end{aligned}$$

We conclude that

$$\begin{aligned} \sum _{j=0}^\infty \frac{|u_j(r)|^2}{r^2}&\le \frac{1}{d-2}\left( \frac{1}{(\gamma -\gamma _{j_0}^-)^2}+\frac{1}{(\gamma _{j_0+1}^- -\gamma )^2}\right) r^{-2\gamma -2}. \end{aligned}$$

Therefore, since $\gamma > d-2$,

$$\begin{aligned} \frac{1}{R^d}\int _{|x|\ge R}\frac{|u|^2}{|x|^2}\, dx&=\frac{1}{R^d}\int _R^\infty \left( \sum _{j=0}^\infty \frac{|u_j(r)|^2}{r^2}\right) \, r^{d-1}\, dr \\&\le \frac{1}{d-2}\left( \frac{1}{(\gamma -\gamma _{j_0}^-)^2}+ \frac{1}{(\gamma _{j_0+1}^- -\gamma )^2}\right) \frac{R^{-2\gamma -2}}{2\gamma +2-d}\\&\le \frac{1}{(d-2)^2}\left( \frac{1}{(\gamma -\gamma _{j_0}^-)^2}+ \frac{1}{(\gamma _{j_0+1}^- -\gamma )^2}\right) R^{-2\gamma -2}, \end{aligned}$$

which proves (A.3).