Final epidemic size of a two-community SIR model with asymmetric coupling

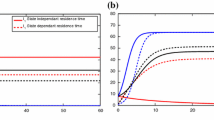
Abstract

Communities are commonly not isolated but interact asymmetrically with each other, allowing the propagation of infectious diseases within the same community and between different communities. To reveal the impact of asymmetrical interactions and contact heterogeneity on disease transmission, we formulate a two-community SIR epidemic model, in which each community has its contact structure while communication between communities occurs through temporary commuters. We derive an explicit formula for the basic reproduction number ${\mathcal {R}}_0$, give an implicit equation for the final epidemic size z, and analyze the relationship between them. Unlike the typical positive correlation between ${\mathcal {R}}_0$ and z in the classic SIR model, we find a negatively correlated relationship between counterparts of our model deviating from homogeneous populations. Moreover, we investigate the impact of asymmetric coupling mechanisms on ${\mathcal {R}}_0$. The results suggest that, in scenarios with restricted movement of susceptible individuals within a community, ${\mathcal {R}}_0$ does not follow a simple monotonous relationship, indicating that an unbending decrease in the movement of susceptible individuals may increase ${\mathcal {R}}_0$. We further demonstrate that network contacts within communities have a greater effect on ${\mathcal {R}}_0$ than casual contacts between communities. Finally, we develop an epidemic model without restriction on the movement of susceptible individuals, and the numerical simulations suggest that the increase in human flow between communities leads to a larger ${\mathcal {R}}_0$.

Appendix

We can obtain the roots of the quaternion equation (3.10) using the Ferrari’s solution (see, https://en.wikipedia.org/wiki/Quartic_function#Ferraris_solution for the exact solution procedure):

$$\begin{aligned} \begin{aligned}&\lambda _1=\frac{\rho _{lA}+\rho _{lB}}{4} +\frac{\sqrt{\mu +2y}+\sqrt{-(3\mu +2y+\frac{2\nu }{\sqrt{\mu +2y}})}}{2},\\&\lambda _2=\frac{\rho _{lA}+\rho _{lB}}{4} +\frac{\sqrt{\mu +2y}-\sqrt{-(3\mu +2y+\frac{2\nu }{\sqrt{\mu +2y}})}}{2},\\&\lambda _3=\frac{\rho _{lA}+\rho _{lB}}{4} -\frac{\sqrt{\mu +2y}+\sqrt{-(3\mu +2y-\frac{2\nu }{\sqrt{\mu +2y}})}}{2},\\&\lambda _4=\frac{\rho _{lA}+\rho _{lB}}{4} -\frac{\sqrt{\mu +2y}-\sqrt{-(3\mu +2y-\frac{2\nu }{\sqrt{\mu +2y}})}}{2}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}&\mu =\frac{1}{8}(-3\rho _{lA}^2+2\rho _{lA}\rho _{lB}-3\rho _{lB}^2-8\rho _{gA}\rho _{gB}),\\&\nu =-\frac{\rho _{lA}\rho _{gA}\rho _{gB}(2\langle k\rangle _A^2-\langle k^2\rangle _A)}{2\langle k^2\rangle _A}-\frac{\rho _{lA}^3-\rho _{lA}^2\rho _{lB}-\rho _{lA}\rho _{lB}^2+\rho _{lB}^3}{8}\\&\quad \; \ \ +\frac{\rho _{lB}\rho _{gA}\rho _{gB} (\langle k^2\rangle _B-2\langle k\rangle _B^2)}{2\langle k^2\rangle _B},\\&\upsilon =-\frac{\rho _{lA}^2\rho _{gA}\rho _{gB}}{16\langle k^2\rangle _A}\big (4\langle k\rangle _A^2-3\langle k^2\rangle _A\big ) -\frac{\rho _{lA}\rho _{lB}\rho _{gA}\rho _{gB}}{8\langle k^2\rangle _A\langle k^2\rangle _B}\big (5\langle k^2\rangle _A\langle k^2\rangle _B -6\langle k\rangle _A^2\langle k^2\rangle _B\\&\quad \; \ \ -6\langle k^2\rangle _A\langle k\rangle _B^2+8\langle k\rangle _A^2\langle k\rangle _B^2\big ) +\frac{1}{256}\big (4\rho _{lA}^3\rho _{lB}+4\rho _{lA} \rho _{lB}^3-3\rho _{lA}^4+14\rho _{lA}^2\rho _{lB}^2-3\rho _{lB}^4\big )\\&\quad \; \ \ +\frac{\rho _{lB}^2\rho _{gA}\rho _{gB}}{16\langle k^2\rangle _B} \big (3\langle k^2\rangle _B-4\langle k\rangle _B^2\big ),\\&y=-\frac{5}{6}\mu -\frac{P}{3U}+U,~~P=-\frac{\mu ^2}{12}-\upsilon ,~~Q =-\frac{\mu ^3}{108}+\frac{\mu \upsilon }{3}-\frac{\nu ^2}{8},\\&U=\root 3 \of {-\frac{Q}{2}\pm \sqrt{\frac{Q^2}{4}+\frac{P^3}{27}}} \text {(take the value with the larger mode)}. \end{aligned}$$