Abstract
We present some essential properties of solutions to the homogeneous Landau-Fermi-Dirac equation for moderately soft potentials. Uniform in time estimates for statistical moments, \(L^{p}\)-norm generation and Sobolev regularity are shown using a combination of techniques that include recent developments concerning level set analysis in the spirit of De Giorgi and refined entropy-entropy dissipation functional inequalities for the Landau collision operator which are extended to the case in question here. As a consequence of the analysis, we prove algebraic relaxation of non degenerate distributions towards the Fermi-Dirac statistics under a weak non saturation condition for the initial datum. All quantitative estimates are uniform with respect to the quantum parameter. They therefore also hold for the classical limit, that is, the Landau equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Setting of the problem
In the ensuing pages we study the essential properties of a dilute gas satisfying Pauli’s exclusion principle in the Landau’s grazing limit regime. More specifically, we study the Landau-Fermi-Dirac (LFD) equation in the homogeneous setting for moderately soft potential interactions described as
where the collision operator \({\mathcal {Q}}\) is given by a modification of the Landau operator which includes Pauli’s exclusion principle. This is defined as
with the usual shorthand \(f:= f(v)\), \(f_* := f(v_*)\), and
The Pauli exclusion principle implies that a solution to (1.11.10) must a priori satisfy the bound
where the quantum parameter
depends on the reduced Planck constant \(\hslash \approx 1.054\times 10^{-34} \mathrm {m}^{2}\mathrm {kg\,s}^{-1}\), the mass m and the statistical weight \(\beta \) of the particles species; see [1, Chapter 17]. In the case of electrons \(\varvec{\varepsilon }\approx 1.93\times 10^{-10}\ll 1\). The parameter \(\varvec{\varepsilon }\) quantifies the quantum effects of the model. The case \(\varvec{\varepsilon }=0\) corresponds to the classical Landau equation.
In this paper, we are interested in moderately soft potentials, corresponding to the case when \(\gamma \in (-2,0)\). The main original features of this paper are:
-
It is the first systematic study of the LFD equation for moderately soft potentials, which are a class of potentials essentially closer to the most relevant case of Coulomb interactions than the recently studied hard potentials case, see [2].
-
Pointwise bounds are obtained thanks to a variant of the De Giorgi method, which leads to an elegant proof in which no high-order derivatives are manipulated. Such \(L^{\infty }\)-estimates are actually independent of the quantum parameter \(\varvec{\varepsilon }\) and yield the following pointwise lower bound
$$\begin{aligned} \inf _{v \in {\mathbb {R}}^{3}}\left( 1-\varvec{\varepsilon }f(t,v)\right) \geqslant \kappa _{0} >0\,, \qquad \forall t \geqslant 1, \end{aligned}$$(1.3)which plays a fundamental role in the long-time behaviour analysis.
-
Stretched exponential decay towards equilibrium is recovered thanks to a careful analysis of the constants pertaining to the moments bounds and to a complex interpolation procedure involving a nonstandard Gronwall-like lemma; we point out that, for soft potentials, exponential decay is not expected.
-
All estimates are uniform with respect to the quantum parameter (lying in a range fully determined by properties of the initial datum such as statistical moments and entropy), so that the statements and proofs also hold for the Landau equation with moderately soft potentials. This provides a new approach for classical and novel results concerning this equation, in particular related to the long time behaviour.
Concerning the smallness of the parameter in the above point, let us make clear to the reader that our approach does not resort to any kind of perturbation argument. The smallness of \(\varvec{\varepsilon }\) has to be interpreted rather as a saturation condition since we need to ensure that \(\varvec{\varepsilon }\) lies in some physical range for which the above (1.3) holds. In particular, this restriction on the range of parameters will be needed here only for the results regarding convergence towards equilibrium.
Before going further in the description of our results and the related literature on the field, let us comment a little bit on the terminology we adopt and the physical relevance of our results. As far as the classical Landau equation is concerned, the physically relevant potential interaction is the one associated to Coulomb interactions, corresponding to the choice \(\gamma =-3\). This is well-documented in the plasma physics literature, and has been observed for instance in [3] in the context of the derivation of the Landau equation from a N particles system. Under such a premise, it may appear artificial to choose the range of parameters \(\gamma \in (-2,0)\) for our analysis and to refer to it as “moderately soft potentials”. The choice of this terminology is motivated by the fact that the Landau-Fermi-Dirac equation (1.11.10) can be derived at the formal level from the Boltzmann-Fermi-Dirac equation in the grazing collision limit (see [1, 4, 5] for details in the classical case) and, as such, inherits the terminology in use for the Boltzmann Equation [6]. Besides the terminology, the choice of the range of parameters \(-2< \gamma <0\) corresponds to a case in which a well understood theory exists for global, non-perturbative strong solutions of the classical (that is, when \(\varvec{\varepsilon }=0\)) Landau equation (such a theory exists in fact when \(-2 \leqslant \gamma \leqslant 1\), cf. [7, 8]). For \(\gamma < -2\), only weak (or H-) solutions are known to exist [9]. Since the main bounds presented in this work are uniform with respect to \(\varvec{\varepsilon }\), we expect that they cannot easily be extended to the case when \(\gamma < -2\), at least using the same methods. Possible extensions of the De Giorgi approach to derive pointwise bounds will nevertheless be the object of future work by the authors, for models related to the Landau equation. We finally mention the recent work [10] which deals with (1.11.10) for \(\gamma =-3\) in a framework different from ours since the work [10] is dealing with some fixed \(\varvec{\varepsilon }\) and is not concerned with uniform bounds with respect to \(\varvec{\varepsilon }.\)
1.2 Thermal equilibrium
The relevant steady state of the LFD equation is the so-called Fermi-Dirac statistics.
Definition 1.1
(Fermi-Dirac statistics) Given \(\varrho>0, u\in {\mathbb {R}}^3, \theta >0\) satisfying
we denote by \({\mathcal {M}}_{\varvec{\varepsilon }}\) the unique Fermi-Dirac statistics (see [11, Proposition 3] for the proof of existence and uniqueness of such a function)
with \(a_{\varvec{\varepsilon }},\) \(b_{\varvec{\varepsilon }}\) defined in such a way that
Note that \(M_{\varvec{\varepsilon }}\) is here a suitable Maxwellian distribution that allows us to recover in the classical limit \(\varvec{\varepsilon }\rightarrow 0\) the Maxwellian equilibrium.
Besides the Fermi-Dirac statistics (1.5), the distribution
can be a stationary state with prescribed mass \(\varrho =\int _{{\mathbb {R}}^{3}}F_{\varvec{\varepsilon }}(v)\mathrm {d}v\) (where \(|{\mathbb {S}}^{2}|=4\pi \) is the volume of the unit sphere). Such a degenerate state, referred to as a saturated Fermi-Dirac stationary state, can occur for very cold gases (with an explicit condition on the gas temperature). For such saturated states, the condition
makes the inequality (1.4) an identity which enforces
The fact that an initial distribution close to such degenerate state makes \(1-\varvec{\varepsilon }f\) arbitrarily small in non negligible sets affects the diffusion mechanism and the regularisation process induced by the parabolic nature of (1.11.10). As such, the existence of such saturated states impacts the gas relaxation towards the corresponding Fermi-Dirac statistics in a close-to-saturation situation. It was shown in reference [2] that, for hard potentials, explicit exponential relaxation rates exist when \(\varvec{\varepsilon }\in (0,c\,\varvec{\varepsilon }_{\text {sat}})\) for some universal \(c\in (0,1)\). One of the central results of this work is the proof of an analogous statement for moderately soft potentials (with algebraic rates). Proving explicit relaxation rates for \(c=1\) remains an open problem for any potential.
1.3 Notations
For \(s \in {\mathbb {R}}\) and \( p\geqslant 1\), we define the Lebesgue space \(L^{p}_{s}({\mathbb {R}}^3)\) through the norm
where \(\langle v\rangle :=\sqrt{1+|v|^{2}}\), \(v\in {\mathbb {R}}^{3}.\) More generally, for any weight function \(\varpi \,:\,{\mathbb {R}}^{3} \rightarrow {\mathbb {R}}^{+}\), we define, for any \(p \geqslant 1\),
With this notation, one can write for example \(L^{p}_{s}({\mathbb {R}}^{3})=L^{p}\big (\langle \cdot \rangle ^{s}\big )\), for \(p \geqslant 1,\,s \geqslant 0\). We define the weighted Sobolev spaces by
with the standard norm
where \(\beta =(i_1,i_2,i_3)\in {\mathbb {N}}^3\), \(|\beta |=i_1+i_2+i_3\) and \(\partial ^{\beta }_v f =\partial _1^{i_1}\partial _2^{i_2}\partial _3^{i_3} f\). For \(p=2\), we will simply write \(H^{k}_{s}({\mathbb {R}}^{3})=W^{k,2}_{s}({\mathbb {R}}^{3})\), \(k \in {\mathbb {N}}\), \(s \geqslant 0\). An additional important shorthand that will be used when specifically referring to moments and weighted \(L^{2}\)-norm of solutions is defined in the following:
Definition 1.2
Given a nonnegative measurable map** \(g\,:\,{\mathbb {R}}^{3}\rightarrow {{\mathbb {R}}^+}\), we introduce for any \(s \in {\mathbb {R}}\),

and

Moreover, if \(f=f(t,v)\) is a (weak) solution to (1.11.10), we simply write

and  .
.
1.4 Weak solutions for the moderately soft potential case \(\gamma \in (-2,0)\)
In the sequel we perform the calculations in the following functional framework:
Definition 1.3
Fix \(\varvec{\varepsilon }_{0}>0\) and a nonnegative \(f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) satisfying
where \({\mathcal {S}}_{\varvec{\varepsilon }_{0}}(f_{\mathrm{in}})\) denotes the Landau-Fermi-Dirac entropy while \(H(f_{\mathrm{in}})\) is the classical Boltzmann entropy (see Section 2.1 for precise definition).
For any \(\varvec{\varepsilon }\in [0,\varvec{\varepsilon }_{0}]\), we say that \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) if \(f\in L^{1}_{2}({\mathbb {R}}^{3})\) satisfies \(0\leqslant f\leqslant \varvec{\varepsilon }^{-1}\) and
and \({\mathcal {S}}_{\varvec{\varepsilon }}(f) \geqslant {\mathcal {S}}_{\varvec{\varepsilon }}(f_{\mathrm {in}}).\)
By a simple scaling argument, there is no loss in generality in assuming that
This assumption will be made throughout the manuscript and \({\mathcal {M}}_{\varvec{\varepsilon }}\) will always denote the Fermi-Dirac statistics corresponding to this normalisation.
It is important to clarify the role of the class \({\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm{in}})\) in the sequel of the paper as well as that of \(\varvec{\varepsilon }_{0}\). In all the subsequent results, the parameter \(\varvec{\varepsilon }_{0} >0\) is fixed and \(f_{\mathrm{in}}\) satisfying (1.7) is chosen. Then, in several results, we will consider a smaller threshold parameter, say \(\varvec{\varepsilon }_{\star } \in (0,\varvec{\varepsilon }_{0}]\), and solutions \(f=f(t,v)\) to (1.11.10) for all \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }]\). Such solutions will belong to the class \({\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm{in}})\) and properties of such solutions as well as various bounds for them will be derived uniformly with respect to \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }].\) We also wish to point out that, even though our analysis is performed in the physical space \({\mathbb {R}}^{3}\), there is no obstruction to reformulate all our results by considering \(v \in {\mathbb {R}}^{d}\) with \(d \geqslant 2\). The main tools used in our analysis (Sobolev embedding, Nash inequality, etc.) would still apply to this case, yielding only in a change of some of the threshold values \(\varvec{\varepsilon }_{0},\varvec{\varepsilon }_{\star }\) appearing in the paper. For the clarity of exposition, we restrict ourselves to the case \(d=3\).
We adopt the notations of [2], namely,
For any \(f \in L^{1}_{2+\gamma }({\mathbb {R}}^{3})\), we define then the matrix-valued map**s \(\varvec{\sigma }[f]\) and \(\varvec{\Sigma }[f]\) given by
In the same way, we set \(\varvec{b}[f]\,:\,v \in {\mathbb {R}}^{3} \mapsto \varvec{b}[f](v) \in {\mathbb {R}}^{3}\) given by
We also introduce
We emphasise the dependency with respect to the parameter \(\gamma \) in \(\varvec{c}_{\gamma }[f]\) since, in several places, we apply the same definition with \(\gamma +1\) replacing \(\gamma \).
With these notations, the LFD equation can then be written alternatively under the form
Definition 1.4
Consider a non trivial initial datum \(f_{\mathrm {in}} \in L^{1}_{2}({\mathbb {R}}^{3})\) satisfying (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\) and let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\). A weak solution to the LFD Equation (1.11.10) is a function \(f\,:\,{\mathbb {R}}^{+}\times {\mathbb {R}}^{3}\rightarrow {\mathbb {R}}^{+}\) satisfying the following conditions:
-
(i)
\(f \in L^{\infty }({\mathbb {R}}^{+};L^{1}_{2}({\mathbb {R}}^{3})) \bigcap {\mathscr {C}}({\mathbb {R}}^{+},{\mathscr {D}}'({\mathbb {R}}^{3}))\),
-
(ii)
\(f(t) \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) for any \(t \geqslant 0\) and \(f(0)=f_{\mathrm {in}}\),
-
(iii)
The map** \(t\mapsto {\mathcal {S}}_{\varvec{\varepsilon }}(f(t))\) is non-decreasing,
-
(iv)
For any \(\varphi =\varphi (t,v) \in {\mathscr {C}}_{c}^{2}([0,T)\times {\mathbb {R}}^{3})\),
$$\begin{aligned}&-\int _{0}^{T}\mathrm {d}t\int _{{\mathbb {R}}^{3}}f(t,v)\partial _{t}\varphi (t,v)\, \mathrm {d}v-\int _{{\mathbb {R}}^{3}}f_{\mathrm {in}}(v)\varphi (0,v)\mathrm {d}v\nonumber \\&\quad =\int _{0}^{T}\mathrm {d}t \int _{{\mathbb {R}}^{3}}\sum _{i,j}{\vec {\Sigma }}_{i,j}[f(t)]f(t,v) \partial ^{2}_{v_{i},v_{j}}\varphi (t,v)\mathrm {d}v\nonumber \\&\qquad + \sum _{i=1}^{3}\int _{0}^{T}\,\mathrm {d}t\int _{{\mathbb {R}}^{6}}f(t,v)f(t,w)(1-{\vec {\varvec{\varepsilon }}} f(t,w)){\vec {b}}_{i}(v-w)\nonumber \\&\qquad \left[ \partial _{v_{i}}\varphi (t,v) -\partial _{w_{i}}\varphi (t,w)\right] \,\mathrm {d}v\,\mathrm {d}w. \end{aligned}$$(1.11)
Notice that, since \(f(t) \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm{in}})\), one has in particular \(0 \leqslant f(t) \leqslant \varvec{\varepsilon }^{-1}\) for any \(t \geqslant 0\). Since \(\varphi \) has compact support together with its derivatives, all the terms in (1.11) are well defined.
1.5 Main results
As mentioned, we study the existence, uniqueness, smoothness, large velocity and large time behavior of solutions to the spatially homogeneous Landau-Fermi-Dirac Equation (1.11.10) with moderately soft potentials. We now present our main results and insist that all estimates provided are uniform in the vanishing limit of the quantum parameter \(\varvec{\varepsilon }\).
We start with a result regarding the existence of weak solutions.
Theorem 1.5
Let \(\gamma \in (-2,0]\). Consider an initial datum \(f_{\mathrm {in}}\in L^1_{s_0}({\mathbb {R}}^3)\) for some \(s_0>2\) satisfying (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\). Then, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) there exists a weak solution f to (1.11.10) and one has \(f\in L^\infty _{\mathrm {loc}}({\mathbb {R}}_+,L^1_{s_0}({\mathbb {R}}^3))\).
The proof of this existence result can be found in Appendix B. It follows the same lines as the proof of the analogous theorem in the hard potential case in [12]. We recall that for the classical Landau equation (that is for \(\varvec{\varepsilon }=0\)) the theory of existence for the case when \(\gamma <-2\) (very soft potentials) is substantially different from the case \(\gamma > -2\) (moderately soft potentials) [8, 9]; we do not investigate the LFD equation with very soft potentials in this paper.
We now turn to a result of smoothness which holds uniformly with respect to \(\varvec{\varepsilon }\), for any given time interval [0, T], with \(T>0\). Uniformity with respect to T is not obtained at this level, and is considered only in next result.
Theorem 1.6
Let \(\gamma \in (-2,0)\). Consider an initial datum \(f_{\mathrm {in}}\in L^1_{s}({\mathbb {R}}^3) \cap L^{q_0}({\mathbb {R}}^3)\) for all \(s \geqslant 0\) and some \(q_0\geqslant 2\), satisfying (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\). Then, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\), any weak solution to Equation (1.11.10) constructed in Theorem 1.5 lies in \(L^{\infty }([0,T]; L^q_s({\mathbb {R}}^3))\) for all \(s\geqslant 0\), \(q \in [1,q_{0})\) and \(T>0\).
Moreover if the initial datum \(f_{\mathrm {in}}\) also lies in \(W^{1,p}_s({\mathbb {R}}^3)\) for all \(s\geqslant 0\) and all \(p \in [1, \infty )\), any weak solution constructed in Theorem 1.5 is unique and lies in \(L^{\infty }([0,T]; W^{1,p}_s({\mathbb {R}}^3)) \cap {L^2}([0,T]; H^{2}_s({\mathbb {R}}^3))\) for all \(s\geqslant 0\), \(p \in [1, \infty )\) and \(T>0\), as well as in \({\mathscr {C}}^{0,\alpha }([0,T] \times {\mathbb {R}}^3)\) for some \(\alpha \in (0,1)\) and all \(T>0\). Finally, all the norms of f in the spaces described in this Theorem are uniform with respect to \(\varvec{\varepsilon }\in [0,\varvec{\varepsilon }_0]\) and depend on the \(W^{1,p}_s({\mathbb {R}}^3)\) norms of \(f_{\mathrm{in}}\) as well as \(H(f_{\mathrm{in}})\).
The fact that the solution \(f=f(t,v)\) belongs to \({\mathscr {C}}^{0,\alpha }([0,T] \times {\mathbb {R}}^{3})\) can be used to show that f is in fact a classical solution. The proof of this result of propagation of regularity can be found in Appendix A, see in particular Corollary A.8. It follows the methods used in [8] and [9]. Notice that stability (for finite intervals of time) and consequently uniqueness can be investigated thanks to the study of smoothness (for sufficiently smooth initial data).
It can be improved in many directions: The assumptions on initial data can be changed (cf. the various propositions in Appendix A); Appearance of regularity can be shown (this can also be seen in the various propositions in Appendix A); The dependence w.r.t. time of the estimates can be obtained explicitly (and involves only powers and no exponentials, since Gronwall’s lemma is not used), we refer to next theorem for the use of the large time behavior for obtaining uniformity w.r.t. time when (polynomial) moments of sufficient order are initially finite. Note that stretched exponential moments can be considered instead of algebraic moments, as is done in Section 6.
Concerning the long-time behaviour of the solution to (1.11.10), the main result of this work can be summarised in the following theorem:
Theorem 1.7
Assume that \(\gamma \in \left( -2,0\right) \) and consider a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\), with moreover \(f_{\mathrm{in}} \in L^{1}_{s}({\mathbb {R}}^{3})\) with \(s > 14+6|\gamma |.\) Then, there exists \(\varvec{\varepsilon }_{\star } \in (0,\varvec{\varepsilon }_{0}]\) depending only on \(f_{\mathrm {in}}\) through its \(L^{1}_{s}\)-norm such that for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }]\), any nonnegative weak solution \(f:= f(t,v)\) to (1.11.10) constructed in Theorem 1.5 satisfies
-
(1)
No Saturation :
$$\begin{aligned} \kappa _{0} := 1 - \varvec{\varepsilon }\,\sup _{t\geqslant 1}\Vert f(t) \Vert _{\infty }>0. \end{aligned}$$ -
(2)
Algebraic Relaxation : there exists \(C>0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and s such that
$$\begin{aligned} {\mathcal {H}}_{\varvec{\varepsilon }}(f(t)|{\mathcal {M}}_{\varvec{\varepsilon }}) \leqslant C\,\left( 1+t\right) ^{ {-\frac{s-8-6|\gamma |}{2|\gamma |}}}\,, \qquad t \geqslant 1\,, \end{aligned}$$which implies, in particular, that
$$\begin{aligned} \left\| f(t)-{\mathcal {M}}_{\varvec{\varepsilon }}\right\| _{L^{1}} \leqslant \sqrt{2C}\,\left( 1+t\right) ^{{-\frac{s-8-6|\gamma |}{4|\gamma |}}}\,, \qquad t \geqslant 1. \end{aligned}$$
Finally, if
then there exists a constant \(C(\gamma ,s,f_{\mathrm {in}})\) depending on \(H(f_{\mathrm{in}})\), s, \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{r}}\) such that, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star })\)
We emphasise that the constants used above do not depend on \(\varvec{\varepsilon }\).
Notice that it is possible to interpolate the decay towards equilibrium in \(L^1\) and estimate (1.12) in order to get a decay towards equilibrium in \(L^p\), for any \(p \in (1, \infty )\), for suitable initial data.
The result of no saturation described above is crucial for the LFD equation. It was obtained in [2] in the case of hard potentials using an indirect approach based on the analysis of higher regularity of solutions to ensure an \(L^{\infty }\)-bound independent of \(\varvec{\varepsilon }\) by Sobolev embedding. In this work the approach is direct; it uses on one hand a careful study of the \(L^1\) and \(L^2\) moments of the solution of the equation, and on the other hand an original use of De Giorgi’s level set method, see Theorem 1.10 hereafter for more details. In both cases, a repeated use of the following technical result will be made.
Proposition 1.8
Assume that \(-2< \gamma < 0\) and \(f_{\mathrm{in}}\) satisfies (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\). For any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\), any \(g \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) and any smooth and compactly supported function \(\phi \), there is \(C_{0} >0\) (depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\)) such that
The above inequality (1.13) has been established in [13, Theorem 2.7] with harmonic analysis tools and study of \(A_{p}\)-weights. This inequality is referred to as a \(\delta \)-Poincaré inequality in [13]. The proof of [13] can be applied without major difficulty to the Landau-Fermi-Dirac context. We nevertheless provide here an elementary proof, based in particular on Pitt’s inequality [14], with a slightly sharper estimate (1.13). On the counterpart, our method seems to apply only for the range of parameters considered here, i.e. \(-2< \gamma < 0\). Related convolution inequalities will be then established in Section 2.3 and exploited for the implementation of the De Giorgi method in Section 4.
The aforementioned proposition plays a fundamental role in the establishment of the following \(L^{1}\)-\(L^{2}\) moments estimates for the solutions to (1.11.10):
Theorem 1.9
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Assume that
Then, there exists a positive constant \(\varvec{C}_{s} >0\) depending on s and \(f_{\mathrm {in}}\) through \(\varvec{m}_{s}(0)\), \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) such that
Moreover, there exists \(\beta _{1} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\varvec{m}_{\frac{3|\gamma |}{2}}(0)\) such that, for \(s > 6+|\gamma |\),
It is worth noticing that Theorem 1.9 shows the instantaneous appearance of weighted \(L^{2}\)-norms independent of \(\varvec{\varepsilon }\). Similar to hard potentials [2], we are required to investigate simultaneously the evolution of the \(L^{1}\) and \(L^{2}\) moments through the evolution of  since the quantum parameter \(\varvec{\varepsilon }\) induces a strong coupling between the two kinds of moments. Our estimate shows a linear time growth of the combined \(L^{1}\) and \(L^{2}\) moments which depends on the moment of order s only through the pre-factor \(C_{s}\). Such a bound is fundamental for the proof of the main Theorem 1.7 which combines its slowly increasing character with an interpolation technique based upon an entropy/entropy production estimate established in [15]. The use of such an interpolation process is typical of soft potential cases for kinetic equations (and briefly described in [15]). Notice that combining the relaxation result together with the aforementioned slowly increasing bound proves, a posteriori, the uniform-in-time estimate (1.12).
since the quantum parameter \(\varvec{\varepsilon }\) induces a strong coupling between the two kinds of moments. Our estimate shows a linear time growth of the combined \(L^{1}\) and \(L^{2}\) moments which depends on the moment of order s only through the pre-factor \(C_{s}\). Such a bound is fundamental for the proof of the main Theorem 1.7 which combines its slowly increasing character with an interpolation technique based upon an entropy/entropy production estimate established in [15]. The use of such an interpolation process is typical of soft potential cases for kinetic equations (and briefly described in [15]). Notice that combining the relaxation result together with the aforementioned slowly increasing bound proves, a posteriori, the uniform-in-time estimate (1.12).
In fact, to prove the no-saturation result of Theorem 1.7, the key point is the following pointwise estimate:
Theorem 1.10
Assume that \(f_{\mathrm {in}}\) satisfies (1.7)–(1.9) with \(\varvec{\varepsilon }_{0} >0\). For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\), let f(t, v) be a weak solution to (1.11.10). Let \(s > \frac{3}{2}|\gamma |\) be given and assume that \(f_{\mathrm {in}} \in L^{1}_{s}({\mathbb {R}}^{3})\). Then, there is a positive constant C depending only on s, \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) such that, for any \(T> t_{*} >0\),
We mentioned previously that we prove Theorem 1.10 thanks to an original use of the level set method of De Giorgi [16] which is a well-known tool for parabolic equations, see the recent surveys [17, 18], and became quite recently efficient for the study of spatially inhomogeneous kinetic Equations [13, 19]. In the spatially homogeneous situation considered here, the method has the flavour of the approach introduced in [20] for the Boltzmann equation, and recently extended to the inhomogeneous framework in [21]. The implementation of the level set method uses a new critical parameter \(\gamma = - \frac{4}{3}\), which is possibly of technical nature, but could be significant even if the physical meaning of such a threshold value remains unclear. We also point out that, this special value \(\gamma =-\frac{4}{3}\) is specific to the physical dimension \(d=3\) and, very likely, another threshold value would appear in dimension \(d \ne 3\). If \(\gamma > -\frac{4}{3}\) indeed, one can pick here above \(s=2\) so that \(\sup _{t\geqslant 0}\varvec{m}_{s}(t) < \infty \), and, of course, (1.16) yields a pointwise estimate for f(t) independent of both T and \(\varvec{\varepsilon }\), proving in a direct way the saturation property in Theorem 1.7.
It is worth noticing that a related pointwise estimate has been obtained in the classical case \(\varvec{\varepsilon }=0\) in [13] for the range \(-2 \leqslant \gamma <0.\) Namely, for solutions f(t) to the classical Landau equation in \({\mathbb {R}}^{3}\), [13, Theorem 2.1] asserts that there exists \(C >0\) such that
Clearly, our method of proof applies directly to this case and, in some sense, improves the result of [13] since combining (1.16) with the uniform bound on the moments (1.12) yields the bound
This eliminates the need of the polynomial weight \(\langle v\rangle ^{-\frac{3}{2}|\gamma |},\) at the price of a slightly worse estimate for the short-time behaviour (notice that since \(s >\frac{3}{2}|\gamma |\), we have \(\frac{3s}{4s-3|\gamma |}+\frac{3}{4} >\frac{3}{2}\)).
We indicate that if stretched exponential moments initially exist, then the convergence towards equilibrium can be proved to have a stretched exponential rate as well, similar to related works on the Landau equation, see for example [22]. A precise result is given in Theorem 6.10. We mention here that such a result uses again interpolation technique between slowly increasing bounds for \(L^{1}\) and \(L^{2}\) weighted estimates for the solution to (1.11.10) and the entropy/entropy production. The slowly increasing bounds for moments associated to stretched exponential weights is deduced directly from Theorem 1.9 by exploiting the fact that we kept track of the dependence of \(\varvec{C}_{s}\) in terms of s in (1.15).
1.6 Organization of the paper
After this Introduction, the paper is organized as follows. Section 2 collects several known results about the Fermi-Dirac entropy and the entropy production associated to (1.11.10) and solutions to (1.11.10). We also present in this Section the proof of the technical result stated in Proposition 1.8 as well as some other related convolution estimates. Section 3 is devoted to the study of both the \(L^{1}\) and \(L^{2}\) moments of solutions to (1.11.10), culminating with the proof of Theorem 1.9. In Section 4 we implement De Giorgi’s level set methods resulting in Theorem 1.10 whereas in Section 5 we collect the results of the previous sections which, combined with the study of the entropy production performed in [15], allow to derive the algebraic convergence towards equilibrium in Theorem 1.7. We upgrade this rate of convergence in Section 6 showing a stretched exponential rate of convergence for solutions associated with initial datum with finite stretched exponential moments. The paper ends with two Appendices. Appendix A is devoted to some additional regularity estimates for solutions to (1.11.10) resulting in Theorem 1.6. The full proof of Theorem 1.5 is then postponed to the Appendix B.
2 Preliminary Results
2.1 Boltzmann and Fermi-Dirac Entropy and entropy production
Recall the classical Boltzmann entropy
The Fermi-Dirac entropy is introduced as
The Fermi-Dirac relative entropy is defined as follows: given nonnegative \(f,\,g \in L^1_2({\mathbb {R}}^3)\) with \(0 \leqslant f \leqslant \varvec{\varepsilon }^{-1}\) and \(0 \leqslant g \leqslant \varvec{\varepsilon }^{-1}\), set
For the Fermi-Dirac relative entropy, a two-sided Csiszár-Kullback inequality holds true (see [23, Theorem 3]). There exists \(C >0\) (depending only on \(\varvec{\varepsilon }\) and \(\Vert g\Vert _{L^{1}_{2}}\)) such that
The long time behaviour of the solutions of the equation will be studied using the classical method consisting in comparing the relative entropy with the entropy production. In our case, the entropy production is defined as
One can show that
for any smooth function \(0< g < \varvec{\varepsilon }^{-1}\), with
A thorough analysis of the link between the Landau-Fermi-Dirac entropy and its entropy production \({\mathscr {D}}_{\varvec{\varepsilon }}\) has been established by the authors in a previous contribution [15], and we refer to the op. cit. for more details on the topic.
2.2 General estimates
One has the following result, refer to [2, Lemma 2.3 & 2.4].
Lemma 2.1
Let \(0\leqslant f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) be fixed and satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Then, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\), the following hold:
-
(1)
For any \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), it holds that
$$\begin{aligned} \inf _{0<\varvec{\varepsilon }\leqslant \varvec{\varepsilon }_{0}}\int _{|v|\leqslant R(f_{\mathrm {in}})} f(1-\varvec{\varepsilon }f)\, \mathrm {d}v \geqslant \eta (f_{\mathrm {in}})>0\,, \end{aligned}$$(2.6)for some \(R(f_{\mathrm {in}})>0\) and \(\eta (f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\) but not on \(\varvec{\varepsilon }\).
-
(2)
For any \(\delta >0\) there exists \(\eta (\delta )>0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\) such that for any \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), and any measurable set \(A\subset {\mathbb {R}}^3\),
$$\begin{aligned} |A|\leqslant \eta (\delta ) \Longrightarrow \int _A f(1-\varvec{\varepsilon }f)\, \mathrm {d}v \leqslant \delta . \end{aligned}$$(2.7)
A consequence of Lemma 2.1 is the following technical result which will be used for the study of moments.
Lemma 2.2
Let \(0\leqslant f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) be fixed and bounded satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Let \(\gamma <0\). Then, there exists \(\eta _{\star } >0\) depending only on \(H(f_{\mathrm {in}})\) and \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\) such that, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and any \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), one has
Proof
For simplicity, given \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), we set \(F=f(1-\varvec{\varepsilon }\,f)\). From Lemma 2.1,
Let \(v \in {\mathbb {R}}^{3}\) be fixed and define the probability measure \(\mathrm {d}\mu \) over \({\mathbb {R}}^{3}\) by
We introduce the convex function \(\Phi (r)=(1+r)^{\frac{\gamma }{2}}\), \(r >0\). One has, thanks to Jensen’s inequality,
Now,
and, since \(\Phi \) is nonincreasing,
where we used that \(\varrho _{F} \leqslant 1\) thanks to (1.9) and \(\Phi (r)\geqslant (2r)^{\frac{\gamma }{2}}\) for \(r>1\). Since \(\varrho _{F}^{1-\frac{\gamma }{2}} \geqslant \eta (f_{\mathrm {in}})^{\frac{2-\gamma }{2}}\) the result follows with \(\eta _{\star }= {12^{\frac{\gamma }{2}}}\eta (f_{\mathrm {in}})^{\frac{2-\gamma }{2}} >0.\) \(\square \)
The following coercivity estimate for the matrix \(\varvec{\Sigma }[f]\) holds. Its proof is a copycat of [24, Proposition 2.3] applied to \(F=f(1-\varvec{\varepsilon }f)\) after using Lemma 2.1 appropriately.
Proposition 2.3
Let \(0\leqslant f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) be fixed and satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Then, there exists a constant \(K_{0} > 0,\) depending on \(H(f_{\mathrm {in}})\) and \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) but not \(\varvec{\varepsilon }\), such that
holds for any \(\varvec{\varepsilon }\in [0, \varvec{\varepsilon }_0]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\).
2.3 Convolution inequalities
We establish here some of the main technical tools used in the paper. We begin with the proof of Proposition 1.8 stated in the introduction, which provides suitable estimates on the zero-th order term \(\varvec{c}_{\gamma }[g]=-2(\gamma +3)|\cdot |^{\gamma }*g\).
Proof of Proposition 1.8
Let \(g \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) be fixed. For a given nonnegative \(\phi \), set
For any \(v,v_{*}\in {\mathbb {R}}^{6}\), if \(|v-v_{*}| < \frac{1}{2}\langle v\rangle \), then \(\langle v\rangle \leqslant 2\langle v_{*}\rangle \), and we deduce from this, see [25, Eq. (2.5)],
Thanks to this inequality, we get \(I[\phi ] \leqslant 6\cdot 2^{-\gamma }\left( I_{1}+I_{2}\right) \), with
while
Set \(\psi (v)=\langle v\rangle ^{\frac{\gamma }{2}}\phi (v)\), from which we get that
According to Pitt’s inequality which reads, in \({\mathbb {R}}^{n}\), \(\int _{{\mathbb {R}}^{n}}|x|^{-\alpha }|f(x)|^{2}\mathrm {d}x \lesssim \int _{{\mathbb {R}}^{n}}|\xi |^{\alpha } \,\left| {\widehat{f}}(\xi )\right| ^{2}\mathrm {d}\xi \) for any \(0< \alpha < n\), [14], there is a universal constant \(c >0\) such that, for any \(v_{*}\in {\mathbb {R}}^{3}\),
where \(\tau _{v_{*}}\psi (\cdot )=\psi (\cdot -v_{*}).\) Since \(|\widehat{\tau _{v_{*}}\psi }(\xi )|=|{\widehat{\psi }}(\xi )|\), we get
This results in
where we used that \(-\gamma < 2\). Now, for any \(R >0\), we split the above integral J in Fourier variable as
On the one hand, using Parseval identity, \(J_{1} \leqslant R^{-\gamma }\Vert \psi \Vert _{L^{2}}^{2}=R^{-\gamma }\Vert \langle \cdot \rangle ^{\gamma }\phi ^{2}\Vert _{L^{1}}.\) On the other hand,
that is, \({J}_{2}\leqslant R^{-(2+\gamma )}\left\| \nabla \psi \right\| _{L^{2}}^{2}.\) Thus,
and
for any \(R >0\). This proves (1.13) with \(\delta =6\cdot 2^{-\gamma }{\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}}cR^{-(2+\gamma )}=6\cdot 2^{2-\gamma }cR^{-(2+\gamma )}.\) \(\square \)
An alternative version of the above estimate involving \(L^{p}\)-norms instead of Pitt’s inequality is given by the next Proposition, which now holds for the whole range of parameters between \((-3,0)\). In the sequel, we call the parameter \(\lambda \in (-3,0)\) instead of \(\gamma \) since we will apply the inequality later to \(\lambda =\gamma \), \(\lambda =\gamma +1\), etc..
Proposition 2.4
Let \(\lambda >-3\) and \(p>1\) be such that \(-\lambda \,q<3\) where \(\frac{1}{p}+\frac{1}{q}=1\). Then there exists \(C_{p}(\lambda ) >0\) such that
Proof
For \(\lambda \geqslant 0\), the result is trivial since \(|v-v_{*}| \leqslant \langle v\rangle \,\langle v_{*}\rangle \) for any \(v,v_{*}\in {\mathbb {R}}^{3}.\) Let us consider the case \(-3<\lambda < 0.\) We can assume without loss of generality that \(\varphi \) and g are nonnegative. Write
Using the inequality \(\langle v \rangle \leqslant \sqrt{2} \langle v - v_{*}\rangle \langle v_{*}\rangle ,\) which holds for any \(v,v_{*}\in {\mathbb {R}}^{3}\), we get
For a given \(v_{*}\in {\mathbb {R}}^{3}\), on the set \(\{|v-v_{*}| \geqslant 1\}\), we have \(|v-v_{*}| \leqslant \langle v-v_{*}\rangle \leqslant \sqrt{2}\, |v-v_{*}|\) so that
For a given \(v_{*}\in {\mathbb {R}}^{3}\), on the set \(\{|v - v_{*}|<1\}\), we have \(\langle v -v_{*}\rangle \leqslant \sqrt{2}\). Then, thanks to Hölder’s inequality,
from which we deduce that
This gives the result with \(C_{p}(\lambda ) :=2^{-\lambda }\max \left( 1,\left( \frac{|{\mathbb {S}}^{2}|}{3+\lambda \,q}\right) ^{\frac{1}{q}}\right) .\) \(\square \)
2.4 Consequences
An important first consequence of Proposition 1.8 is the following weighted Fisher estimate. Notice that a similar result can be deduced (for a larger range of parameters \(\gamma <0\)) from an alternative representation of the entropy in the spirit of [26, Theorem 2], refer to [15] for further details.
Proposition 2.5
Let \(0\leqslant f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) be fixed and bounded satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Assume that \(-2< \gamma <0\) and \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\). Then, there is a positive constant \(C_{0}(\gamma )\) depending only on \(f_{\mathrm {in}}\) through \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\), such that for all \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\),
Proof
Let us fix \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\). Recall from (2.3) that
where we recall that \({\mathcal {Q}}(f)=\nabla \cdot \left( \varvec{\Sigma }[f]\nabla f - \varvec{b}[f]\,F\right) \), \(F=f(1-\varvec{\varepsilon }f)\). Therefore,
Using Proposition 2.3, because \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), one has
and, recalling \(\nabla \cdot \varvec{b}[f]=\varvec{c}_{\gamma }[f]\), we deduce from (2.11) that
Then, applying Proposition 1.8, with \(g=f\) and \(\phi =\sqrt{f}\), there is \(C_{0} >0\) such that, for any \(\delta >0\),
Using that
we can choose \(\delta >0\) small enough so that
for some positive constant \(C_{1}(\gamma )\) depending only on \(f_{\mathrm {in}}\). This gives the result. \(\square \)
A significant consequence of the above result is the following corollary which regards solutions to the Landau-Fermi-Dirac Equation (1.11.10).
Corollary 2.6
Assume \(-2< \gamma < 0\) and let \(f_{\mathrm{in}}\) be a nonnegative initial datum satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f(t,\cdot )\) be a weak solution to Landau-Fermi-Dirac equation, then for \(0< t_{1}< t_{2}\),
where \(C_{0}(\gamma )\) is defined in Proposition 2.5. As a consequence, there exist positive constants \({\widetilde{C}}_{0}\) and \({\widetilde{C}}_{1}\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm {in}})\) so that for \(0< t_{1}< t_{2}\),
and
Proof
The first inequality follows by simply integrating the inequality in Proposition 2.5. In order to get the second inequality, we use part (iii) of Definition 1.4, which ensures that
Now, on the one hand,
and
On the other hand,
Hence,
It follows from [2, Appendix A] that \(a_{\varvec{\varepsilon }}\) and \(b_{\varvec{\varepsilon }}\) are uniformly bounded with respect to \(\varvec{\varepsilon }\). This means that \( {\mathcal {S}}_{\varvec{\varepsilon }}({\mathcal {M}}_{\varvec{\varepsilon }})-{\mathcal {S}}_{\varvec{\varepsilon }}(f_{\mathrm {in}}) \leqslant c_{0} < \infty ,\) and the second inequality follows with \({\widetilde{C}}_{0}=C_{0}(\gamma )\max (1,c_{0})\) independent of \(\varvec{\varepsilon }\). To prove (2.13), we recall that the following Sobolev inequality
holds for some positive universal constant \(C_{\mathrm {Sob}} >0\). Applying this with \(u=\langle \cdot \rangle ^{\frac{\gamma }{2}}\sqrt{f(t,\cdot )}\) which is such that \(\Vert u\Vert _{L^{6}}^{2}=\Vert \langle \cdot \rangle ^{\gamma }{f(t,\cdot )}\Vert _{L^{3}}\), one gets the result with \({\widetilde{C}}_{1}=C_{\mathrm {Sob}}{\widetilde{C}}_{0}.\) \(\square \)
One can get rid of the degenerate weight in (2.13) to get a mere \(L^{p}\) bound. We refer to [13, Proposition 5.2] for a complete proof.
Lemma 2.7
Assume \(-2< \gamma < 0\) and let \(f_{\mathrm{in}}\) be a nonnegative initial datum satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f(t,\cdot )\) be a weak solution to Landau-Fermi-Dirac equation. Then, there exists \(C >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm {in}})\) such that for \(0< t_{1} < t_{2}\),
holds with \(p=\min \left( \frac{5}{3},\frac{3(2 +|\gamma |)}{2+3|\gamma |}\right) .\)
3 Moments Estimates
We study here the evolution of both \(L^{1}_{s}\) and \(L^{2}_{s}\) moments of weak solutions to (1.11.10). Our goal is to prove Theorem 1.9.
3.1 \(L^{1}\)-Moments
We start with the following basic observation for the study of moments.
Lemma 3.1
Assume \(-2< \gamma < 0\) and let \(f_{\mathrm{in}}\) be a nonnegative initial datum satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f(t,\cdot )\) be a weak solution to Landau-Fermi-Dirac equation. For any \(s >2\), one has
where \(F=f(1-\varvec{\varepsilon }f)\) and, for any nonnegative measurable map**s \(h,g \geqslant 0\) and \(s >2\), we use the notations
Moreover, for any nonnegative g,
Proof
For a convex function \(\Phi \,:\,{\mathbb {R}}^{+} \rightarrow {\mathbb {R}}^{+}\), we get from (1.11.10)
where \(F=f(1-\varvec{\varepsilon }f)\), and
Picking \(\Phi (r) := (1+r)^{\frac{s}{2}}\), one sees that
Now, a symmetry argument shows that
that is,
and, using symmetry again, we get
which gives the new expression for \({\mathscr {J}}_{s,1}(g,g)\).\(\square \)
Remark 3.2
According to Young’s inequality, for \(s >2\) one has \(\langle v\rangle ^{s-2}\langle v_{*}\rangle ^{2} \leqslant \frac{s-2}{s}\langle v\rangle ^{s}+\frac{2}{s}\langle v_{*}\rangle ^{s}\). Thus,
where we used a simple symmetry argument for the last identity. In particular, one sees that
Let us now estimate \({\mathscr {J}}_{s}(f,F)\). The basic observation is the following:
Lemma 3.3
For any \(s \geqslant 0\), \(f\geqslant 0\), \(F=f\,(1 - \varvec{\varepsilon }\,f)\),
with
Proof
This is proven by direct inspection, using that \(F=f(1-\varvec{\varepsilon }f)\), so that
and also
Taking the mean of these two identities gives (3.2). Now, write for simplicity
One has
from which we deduce, by a symmetry argument, that
which gives the desired expression using symmetry again. \(\square \)
We estimate separately the terms involved in (3.2) starting with the terms \({\mathscr {J}}_{s,1}(F,F)\) and \({\mathscr {J}}_{s,1}(f,f)\).
Lemma 3.4
If \(f_{\mathrm {in}}\) satisfies (1.7)–(1.9) for some \(\varvec{\varepsilon }_{0} >0\), for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and any \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\), it holds
where \(F=f(1-\varvec{\varepsilon }\,f)\) and \(\eta _{\star } >0\) is the constant in Lemma 2.2 which depends only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}}).\) In the same way,
Proof
For \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) fixed, we recall that
and replace, as in [24], \(|v-v_{*}|^{\gamma }\) with its regularized version \(\langle v-v_{*}\rangle ^{\gamma }\). This gives
Recall that \(|v-v_{*}|^{\gamma }-\langle v-v_{*}\rangle ^{\gamma } \geqslant 0.\) Using Hölder’s inequality with the measure \(\mathrm {d}\mu (v,v_{*})=F\,F_{*}\left( |v-v_{*}|^{\gamma }-\langle v-v_{*}\rangle ^{\gamma }\right) \mathrm {d}v\mathrm {d}v_{*}\) and \(p=\frac{s}{s-2},\) \(q=\frac{s}{2}\) so that \(1/p+1/q=1\), one gets
which, by symmetry, reads
Consequently, the second term in the right-hand side of (3.5) is nonpositive. Thus,
For \(v \in {\mathbb {R}}^{3}\) fixed, one has
whereas, thanks to Lemma 2.2, \(\int _{{\mathbb {R}}^{3}}F_{*}\langle v-v_{*}\rangle ^{\gamma }\mathrm {d}v_{*}\geqslant \eta _{\star }\langle v\rangle ^{\gamma }.\) This easily gives (3.3). One proves the result in the same way for \({\mathscr {J}}_{s,1}(f,f)\), noticing that the above lower bound still holds if \(f_{*}\) replaces \(F_{*}\), since \(f_{*}\geqslant F_{*}\).\(\square \)
One can evaluate the other terms in (3.2) as presented in the following lemma.
Lemma 3.5
Assume that \(-2< \gamma < 0\) and let \(f_{\mathrm {in}}\) satisfy (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) be given. There is a positive constant \(C_{0} >0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\) such that, for any \(\delta \in (0,1)\) and any \(s >2\),

whereas,

Proof
Recall that
Neglecting the negative term and using that \(\varvec{\varepsilon }\,f^{2}_{*} \leqslant f_{*}\), we obtain
Inequality (3.6) is obtained using Proposition 1.8 with \(g=f_{*}\) and \(\phi (v)=\langle v\rangle ^{\frac{s}{2}}f(v)\) and noticing that \((1+\delta ^{\frac{\gamma }{2+\gamma }}) \leqslant 2\delta ^{\frac{\gamma }{2+\gamma }}\) for any \(\delta \in (0,1)\) since \(\frac{\gamma }{2+\gamma } <0\). The proof of (3.7) is obvious since (thanks to Lemma 3.3)
where we use that, since \(\gamma +2 \in (0,2)\), we have \(|v-v_{*}|^{\gamma +2}\leqslant 2\langle v\rangle ^{\gamma +2}\langle v_{*}\rangle ^{\gamma +2}\). This proves inequality (3.7) where the last inequality obviously comes from \(\varvec{\varepsilon }f^{2} \leqslant f.\) \(\square \)
Let us now investigate the second term \({\mathscr {J}}_{s,2}(f,F)\) in the right-hand side of (3.1).
Lemma 3.6
Assume that \(-2<\gamma < 0.\) Let \(f_{\mathrm {in}}\) satisfy (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\), \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm{in}})\), \(F= f \,(1 - \varvec{\varepsilon }f)\) be given. Then for any \(s >2\),
Proof
Let \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\) be fixed. Recall that
and split the integral according to \(|v-v_{*}| < 1\) and \(|v-v_{*}| \geqslant 1.\) Since
one sees that
For the integral on the set \(|v-v_{*}| <1\), one uses that \(|v|^{2}\,|v_{*}|^{2}-(v\cdot v_{*})^{2} \leqslant |v|\,|v_{*}|\,|v-v_{*}|^{2}\) to get
where we used that \(\gamma +2 \geqslant 0\) to deduce \(|v-v_{*}|^{\gamma +2} \leqslant 1.\) Since, from Young’s inequality,
one deduces the result. \(\square \)
We apply the previous results to solutions f(t, v) to (1.11.10) to obtain the following proposition.
Proposition 3.7
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there is a positive constant \(C >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), such that, for any \(s >2\) and \(\delta \in (0,1)\), there are positive constant \(\varvec{K}_{s}\) which depend on s and \(H(f_{\mathrm{in}})\) and \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) satisfying

Moreover, there exists \(\beta > 0\) depending only on \(H(f_{\mathrm{in}})\) and \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) such that, for \(s\geqslant 3\),
Proof
According to (3.1) and (3.2), one has
with \(f=f(t,v)\) and \(F=f(1-\varvec{\varepsilon }f).\) One sees from (3.3)–(3.4) that
whereas, from (3.6) and (3.7),

for any \(\delta \in (0,1)\). Using then (3.9) to estimate \({\mathscr {J}}_{s,2}(f,F)\), we deduce that

Since \(\gamma +2 >0\), the map** \(v \in {\mathbb {R}}^{3} \mapsto 4\langle v\rangle ^{s-2}-\frac{1}{2}\eta _{\star }\langle v\rangle ^{s+\gamma }\) is bounded by some positive constant \(\varvec{K}_{s} >0\) which depends on \(f_{\mathrm {in}}\) through \(\eta _{\star }\). Thus, we deduce that

with \({\bar{C}}=\max \left( \frac{C_{0}}{2},8\right) .\) Again, since \(\gamma >-2\), up to a modification of \(\varvec{K}_{s}\), we have \(6(s-2) \varvec{m}_{s-2}(t) \leqslant \varvec{K}_{s}+\frac{\eta _{\star }}{4}\varvec{m}_{s+\gamma }(t)\), from which we easily deduce (3.10). Let us now explicit \(\varvec{K}_{s}\). One observes from the aforementioned computations that one can take \(\varvec{K}_{s}=\max (\sup _{x>0}u_{s}(x),\sup _{x>0}w_{s}(x))\), where
It is clear that \(\sup _{x >0}u_{s}(x)=u_{s}({\bar{x}})\) and \(\sup _{x >0}w_{s}(x)=w_{s}({\tilde{x}})\), where
and consequently, \(\sup _{x>0}u_{s}(x)=4{\bar{x}}^{s-2}\frac{\gamma +2}{s+\gamma },\) \(\sup _{x >0}w_{s}(x)=6(s-2){\tilde{x}}^{s-2}\frac{\gamma +2}{s+\gamma }.\) Therefore, for any \(s \geqslant 3\), we see that \(\varvec{K}_{s}=\sup _{x>0}w_{s}(x)\), and one checks that (3.11) holds for some explicit \(\beta >0\). \(\square \)
3.2 \(L^{2}\)-Estimates
We now aim to study the evolution of weighted \(L^{2}\)-norms of f(t, v). Kee** previous notations, we have the lemma.
Lemma 3.8
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). For any \(s \geqslant 0\), it holds that

where \(\varvec{A}(v)=\langle v\rangle ^{2}\mathbf {Id}+(s-2)\,v\otimes v\), \(v \in {\mathbb {R}}^{3}\) and \(K_{0}\) is defined in Proposition 2.3.
Proof
As in [2], for any \(s \geqslant 0\),
Using the uniform ellipticity of the diffusion matrix \(\varvec{\Sigma }[f]\) (recall Proposition 2.3), we deduce that
Moreover, writing
from which
we also have
Therefore, recalling that \(\nabla \cdot \varvec{b}[f]=\varvec{c}_{\gamma }[f]=-2(\gamma +3)|\cdot |^{\gamma }*f\), we get

Let us investigate more carefully the last term. Integration by parts shows that
Using the product rule
where \(D_{v}\big ( \langle v\rangle ^{s-2} v\big )\) is the matrix with entries \(\partial _{v_{i}}\big ( \langle v\rangle ^{s-2} v_{j}\big )\), \(i,j=1,2,3\), or more compactly,
one gets the desired inequality, recalling that \(\varvec{B}[f]=\varvec{b}[f]-\varvec{\varepsilon }\,\varvec{b}[f^{2}].\) \(\square \)
We deduce from the previous arguments
Proposition 3.9
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). There exists some positive constant \({\bar{C}}(f_{\mathrm {in}})\) depending on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\), such that

holds for any \(s \geqslant 0.\)
Proof
We denote by \(I_{1},I_{2},I_{3},I_{4},I_{5}\) the various terms on the right-hand-side of (3.12), i.e.

and we control each term starting from \(I_{1}\). Since \(0 \leqslant \frac{1}{6}f^{2} \leqslant \frac{1}{2}f^{2}-\frac{\varvec{\varepsilon }}{3}f^{3} \leqslant \frac{1}{2}f^{2}\), one has
so that, using Proposition 1.8 with \(g=f(t)\) and \(\phi ^{2}=\langle \cdot \rangle ^{s}f^{2}(t)\), we deduce that, for any \(\delta \in (0,1)\),

where \(C_{1}\) depends on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\). For the term \(I_{2}\), since \(0\leqslant \frac{1}{3}f^{2} \leqslant f^{2}-\frac{2\varvec{\varepsilon }}{3}f^{3} \leqslant f^{2}\), it holds that
Therefore, if \(\gamma +1 <0\), applying Proposition 1.8 with \(\varvec{c}_{\gamma +1}[g]\) instead of \(\varvec{c}_{\gamma }[g]\), and \(g=f(t,v)\), \(\phi ^{2}=\langle \cdot \rangle ^{s-1}f^{2}(t)\), we get

whereas, if \(\gamma +1 >0\), one has obviously  . In both cases, for any \(\delta >0\),
. In both cases, for any \(\delta >0\),

In the same way,
since \(\varvec{\varepsilon }f^{2}\leqslant f.\) Then, as before, for any \(\delta >0\), there is \(C_{1} >0\) such that

For the term \(I_{5}\), one checks easily that, for any \(i,j \in \{1,2,3\}\),
and
One has, since \(\gamma +2 >0\),

Finally, it is easy to see that  . Overall, recalling mass and energy conservation to estimate all the weighted \(L^{1}\)-terms, one sees that, for any \({\delta \in (0,1)}\), there is some positive constant \(C(f_{\mathrm {in}})\) depending on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) (through \(K_{0}\)) such that
. Overall, recalling mass and energy conservation to estimate all the weighted \(L^{1}\)-terms, one sees that, for any \({\delta \in (0,1)}\), there is some positive constant \(C(f_{\mathrm {in}})\) depending on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) (through \(K_{0}\)) such that

For \(s \in [0,1]\), (3.15) can be rephrased simply as

and, picking \(\delta \in (0,1)\) such that \(3\delta \leqslant \frac{K_{0}}{4}\), one deduces that

for some positive constant \({\widetilde{C}}_{\gamma }(f_{\mathrm{in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\gamma \). For \(s >1\), since \(2s+1 \leqslant 3s\), choosing \(\delta :=\min \left( \frac{K_{0}}{16s},1\right) \) we deduce from (3.15) that there is \(C_{\gamma }(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\gamma >0\) such that

From Nash inequality, there is some universal constant \(C >0\) such that

which, thanks to Young’s inequality, implies that there is \(C >0\) such that, for any \(\alpha >0\),

Choosing now \(\alpha >0\) such that \({\widetilde{C}}_{\gamma }(f_{\mathrm{in}})\alpha =\frac{K_{0}}{8}\) if \(s \in [0,1]\) or \(C_{\gamma }(f_{\mathrm {in}})\,\left( s^{2}+{s^{-\frac{\gamma }{2+\gamma }}}{+s+s^{\frac{2}{\gamma +3}}}\right) \alpha = \frac{K_{0}}{8}\) whenever \(s >1\), we end up with

where, according to estimate (3.17) and (3.18),
and the last choice of \(\alpha =\frac{K_{0}}{8C_{\gamma }(f_{\mathrm{in}})}\left( s^{2}+{s^{-\frac{\gamma }{2+\gamma }}}{+s+s^{\frac{2}{\gamma +3}}}\right) ^{-1}\) gives that
since \(\max (1,2,\frac{-\gamma }{2+\gamma },\frac{2}{3+\gamma }) \leqslant \frac{4}{2+\gamma }\) for any \(-2< \gamma <0\) and with \(C(f_{\mathrm {in}})\) and \({\bar{C}}(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\) but not on s. This shows (3.14). \(\square \)
Corollary 3.10
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Given \(s \in [0,4+|\gamma |]\) there exists some positive constant \(C(f_{\mathrm {in}})\) depending on \(f_{\mathrm {in}}\) only through \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\), and such that

holds for any \(0 \leqslant t_{1} < t_{2}\).
Proof
When \(\frac{\gamma +s}{2}\leqslant 2\), it holds that \(\Vert \langle \cdot \rangle ^{\frac{\gamma +s}{2}}f\Vert _{L^1}\leqslant \Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), which gives the statement after integration of (3.14).\(\square \)
3.3 Short-time estimates and appearance of \(L^{2}\)-moments
Before trying to get global-in-time estimates for both \(\varvec{m}_{s}(t)\) and  (with a growing rate independent of s), let us start with the following non-optimal growth that has to be interpreted here as a short-time estimate.
(with a growing rate independent of s), let us start with the following non-optimal growth that has to be interpreted here as a short-time estimate.
Proposition 3.11
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, for any \(s \geqslant 3\),
where the constant \(C(f_{\mathrm {in}})\) depends on \(f_{\mathrm {in}}\) only through \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) but does not depend on s. If \(s \in (2,3)\) (3.19) still holds for \(\gamma \in [-1,0)\) whereas, for \(\gamma \in (-2,-1)\),
for a constant \(C(f_{\mathrm{in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\).
Proof
Recall that, according to (3.1), \(\dfrac{\mathrm {d}}{\mathrm {d}t}\varvec{m}_{s}(t)={\mathscr {J}}_{s,1}(f,F)+{\mathscr {J}}_{s,2}(f,F)\) where, for any \(s \geqslant 2\),
Recall (see Remark 3.2) that
We neglect such absorption terms since we are interested here in the short time propagation of moments. We also recall that, according to (3.7),
Now, to deal with the term \({\mathscr {J}}_{s,1}(f^{2},f^{2})\), we observe that there is \(c >0\) (independent of s) such that
which implies,
where we used that \(a^{s-3}b \leqslant \frac{s-3}{s-2}a^{s-2}+\frac{1}{s-2}b^{s-2} \leqslant a^{s-2}+b^{s-2}\) for any \(a,b >0\), \(s \geqslant 3\) in the last estimate. Using then a symmetry argument, this yields
Therefore, adding estimate (3.21), (3.22), and (3.24), there is some \(C_{1} >0\) such that
Furthermore, recall from Lemma 3.6 that
Consequently, there exists \(C(f_{\mathrm{in}}) >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) such that
for any \(t \geqslant 0\) and any \(s \geqslant 3.\) This leads to (3.19) after integration. Let us now investigate the case \(s \in (2,3)\). If \(\gamma \in [-1,0)\), one simply uses that
to obtain
This estimate is similar to (3.24) and yields again (3.19). For \(s\in (2,3)\) and \(\gamma \in (-2,-1)\), (3.23) implies
which yields
We have \(\varvec{m}_{s+\gamma }(t)\leqslant \varvec{m}_{2}(t)\) and \(\varvec{m}_{3+\gamma }(t)\leqslant \varvec{m}_{2}(t)\) since \(s \in (2,3)\) and \(\gamma \in (-2,-1)\). Consequently, adding estimate (3.21), (3.22) and (3.26) leads to
for some \(C_1 >0\) depending on \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\) (recall \(s \in (2,3)\)). Then,
This yields the desired estimate after integration for \(s \in (2,3)\) and \(\gamma \in (-2,-1)\). \(\square \)
Notice that, besides the above Corollary 3.10, one can also provide the following appearance and short-time bounds for  :
:
Proposition 3.12
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Assume additionally that
Then, there exists a constant \(c_s(f_{\mathrm {in}})\) such that

with moreover,
for some positive constants \(C(f_{\mathrm{in}}), \varvec{C}_{0}\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) (but not on s).
Proof
Let us pick \(s \geqslant 0\) and set \(T_{s}:=\frac{1}{1+s}\). Recall estimate (3.14)

for some positive constant \(C(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). Using a classical interpolation inequality (see (4.6) in the next section), one has

where we used Sobolev’s inequality (2.14). Thus,

For \(s> 4-\gamma >4+\frac{3\gamma }{2}\), we estimate \(\varvec{m}_{\frac{2s-3\gamma }{4}}(t)\) and \(\varvec{m}_{\frac{s+\gamma }{2}}(t)\) using Proposition 3.11. We assume for simplicity that both \(\frac{2s-3\gamma }{4}\) and \(\frac{s+\gamma }{2}\) are larger than 3 to use (3.19) only. This amounts to pick \(s > 6+|\gamma |\). One has
and, in the same way, for \(s>4-\gamma \),
(note that \(\varvec{m}_{\frac{s+\gamma }{2}}(0)<\infty \) because \(\frac{s+\gamma }{2}<\frac{2s-3\gamma }{4} \)). Therefore,

where
The conclusion then follows by a comparison argument. Namely, introducing
and \({\bar{x}}=\left( \frac{{2\varvec{k}_{s}}(f_{\mathrm {in}})}{\varvec{a}_{s}(f_{\mathrm {in}})}\right) ^{\frac{3}{5}}\), one has \(\varvec{\zeta }(x) \leqslant -\frac{\varvec{a}_{s}(f_{\mathrm{in}})}{2}x^{\frac{5}{3}}\) for \(x \geqslant {\bar{x}}\). Fixing \(t_{\star }\in \left( 0,T_{s}\right] \), one has according to (3.30) that

Three cases may occur:
-
i)
if
 , then since \(\varvec{\zeta }({\bar{x}}) <0\), one has
, then since \(\varvec{\zeta }({\bar{x}}) <0\), one has  for any \(t \geqslant t_{\star },\)
for any \(t \geqslant t_{\star },\) -
ii)
if
 and
and  for any \(t \in (t_{\star },T_{s})\), then one has
for any \(t \in (t_{\star },T_{s})\), then one has 
which, after integration, yields
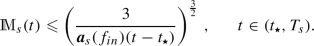
-
iii)
if
 and
and  for some \({\overline{t}}\in (t_{\star },T_{s})\) then, setting
for some \({\overline{t}}\in (t_{\star },T_{s})\) then, setting 
one has, as in the second point, that

Since
 by continuity, we deduce that
by continuity, we deduce that  for all \(t \geqslant T_{\star }\) from the first point.
for all \(t \geqslant T_{\star }\) from the first point.
In all the cases it holds that

from which the result follows by letting \(t_{\star } \rightarrow 0\) and with
with \(\varvec{a}_{s}(f_{\mathrm {in}})\) and \(\varvec{k}_{s}(f_{\mathrm {in}})\) defined in (3.31) with constant \(C(f_{\mathrm{in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). In particular, as far as the dependence with respect to s is concerned, we easily derive (3.28).
If \(\min \left( \frac{2s-3\gamma }{4},\frac{s+\gamma }{2}\right) < 3\), then one has to estimate \(\varvec{m}_{\frac{2s-3\gamma }{4}}(t)\) and/or \(\varvec{m}_{\frac{s+\gamma }{2}}(t)\) using (3.20). The same computations as before allows then to end up again with (3.30) (with slightly different expression for \(\varvec{k}_{s}(f_{\mathrm{in}})\) and \(\varvec{a}_{s}(f_{\mathrm{in}})\)) and get the result as in the previous case. Details are left to the reader. \(\square \)
3.4 Combined estimates
We now introduce

Combining Proposition 3.9 with Proposition 3.7, one gets
Lemma 3.13
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, for any \(s >2\), there are positive constants \(\varvec{K}_{s}, C_{1,s}\) which depend on s and \(f_{\mathrm {in}}\) (through \(H(f_{\mathrm{in}})\) and \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\)) such that

where \({\bar{C}}(f_{\mathrm{in}})\) is the constant in inequality (3.14), \(\varvec{K}_{s}\) was estimated in (3.11), and
for some positive constant \({\bar{C}}_{1}\) depending only on \(f_{\mathrm {in}}\) through \(K_{0}\) and \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\).
Proof
We simply apply (3.10) with \(\delta =\min \left( {\frac{K_{0}}{16s}},1\right) \) and add the obtained inequality with (3.14) to obtain the result. We derive easily the estimate for \(C_{1,s}\) since, for s large enough, \(s\delta =\frac{K_{0}}{16}.\)\(\square \)
We have all in hands to prove Theorem 1.9 in the introduction.
Proof of Theorem 1.9
Let \(s > 4+|\gamma |\). Since \(\frac{2s-3\gamma }{4} \leqslant s\), one has \(\max \left( \varvec{m}_{s}(0),\varvec{m}_{\frac{2s-3\gamma }{4}}(0)\right) =\varvec{m}_{s}(0) < \infty \), and one deduces from Propositions 3.11 and 3.12 that
with
where \(c_{s}(f_{\mathrm{in}})\) and \(C(f_{\mathrm{in}})\) are defined in Propositions 3.12 and 3.11. Since \(s> 4 +|\gamma |\), we use (3.19) and not (3.20). In particular, using that
thanks to Cauchy-Schwarz inequality, we deduce from (3.28) that, for \( s>6+|\gamma |\),
Consequently, there are positive constants \(C_{0},C_{1} >0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
where we used that \(1\leqslant \varvec{m}_{\frac{3|\gamma |}{2}}(0)\). Let us then focus on the evolution of \(\varvec{E}_{s}(t)\) for \(t \geqslant \tfrac{1}{1+s}.\) We start with (3.32) and estimate  and \(\varvec{m}_{\frac{s+\gamma }{2}}^{2}(t)\) as in the proof of Proposition 3.9 (see also [2, Lemma 3.5]). Namely, as seen at the end of the proof of Prop. 3.9, there is a universal constant \(C >0\) independent of s such that, for any \(\delta >0\),
and \(\varvec{m}_{\frac{s+\gamma }{2}}^{2}(t)\) as in the proof of Proposition 3.9 (see also [2, Lemma 3.5]). Namely, as seen at the end of the proof of Prop. 3.9, there is a universal constant \(C >0\) independent of s such that, for any \(\delta >0\),

Inserting this in (3.32) and choosing \(\delta >0\) such that \(C_{1,s}\delta ={\frac{K_{0}}{32}}\), one has

where
Now, for \(s \geqslant 4 -\gamma \),
where we used the conservation of mass and energy. From Young’s inequality, for any \(\delta _{0} >0\), one has then
Choosing now \(\delta _{0} >0\) so that \({\bar{C}}_{3,s}\delta _{0}=s\frac{\eta _{\star }}{8}\), we end up with

where
Integrating this inequality on \(\left( \tfrac{1}{1+s},t\right) \) gives
so that
Proposition 3.11 gives now the second part of (1.14) for small times whereas Proposition 3.12 and (3.36) lead to the second part of (1.14) for large times with
Combining (3.34) with Lemma 3.13, one sees first that there is \(C_{3} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that,
Then, using (3.11) and (3.37), one deduces that there exists \(\beta _{0} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
where we roughly estimate \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}^{\frac{s+\gamma }{2}}\) as \(\beta _{0}^{\frac{8-\gamma }{4+2\gamma }(s+\gamma -2)+1}\) once we notice that \(\frac{s+\gamma }{2} \leqslant {\frac{8-\gamma }{4+2\gamma }(s+\gamma -2)+1}\) for \(s \geqslant 4-\gamma \). Combining these estimates with (3.33) and because \(\frac{s-2}{\gamma +2} < \frac{8-\gamma }{4+2\gamma }(s+\gamma -2)\) for \(s > 4-\gamma \), one deduces easily the estimate (1.15). \(\square \)
Remark 3.14
Of course, if \(f_{\mathrm {in}}\) is actually belonging to \(L^{1}_{s}({\mathbb {R}}^{3}) \cap L^{2}_{s}({\mathbb {R}}^{3})\), then \(\varvec{E}_{s}(0) <\infty \) and one deduces after integration of (3.36) that
The above result shows the linear growth of both the \(L^{1}\)-moments and \(L^{2}\)-moments. Actually, it is possible to sharpen the above estimates (for small s) with the following proposition.
Proposition 3.15
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, for any \(s \in [0,\frac{8+3\gamma }{2}]\),
-
(1)
if \(f_{\mathrm {in}} \in L^{2}_{s}({\mathbb {R}}^{3})\), there is a positive constant \(\varvec{C}_{\mathrm {in}}\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) such that
$$\begin{aligned} \sup _{t\geqslant 0}\Vert f(t)\Vert _{L^{2}_{s}}=\sup _{t\geqslant 0}\left\| \langle \cdot \rangle ^{\frac{s}{2}}f(t,\cdot )\right\| _{L^{2}} \leqslant \varvec{C}_{\mathrm {in}}. \end{aligned}$$(3.38) -
(2)
There are constants \(\varvec{C}_{0,\mathrm {in}}\) and \(\tilde{\varvec{C}}_{\mathrm {in}}\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), and \(H(f_{\mathrm{in}})\) such that for any \(t>0\),
 (3.39)
(3.39)
Proof
Let us pick \(s \in [0,\frac{8+3\gamma }{2}]\). In light of estimate (3.14), since \(\frac{s+\gamma }{2} \leqslant 2,\) we have that

for some positive constant \(\varvec{K}(f_{\mathrm {in}})\) depending only on \(f_{\mathrm {in}}\) through \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). Arguing exactly as in the proof of Proposition 3.12, Equation (3.30) but with \(\varvec{m}_{\frac{2s-3\gamma }{4}}\leqslant \Vert f_{\mathrm {in}}\Vert _{L^1_2}\), one deduces that

where we set \(\kappa _{\mathrm {in}}=K_{0}\left( {4\,C_{\mathrm {Sob}}^{2}\Vert f_{\mathrm{in}} \Vert ^{\frac{4}{3}}_{ L^{1}_{2}}}\right) ^{-1}\). The first point follows then by a simple comparison argument choosing  , whereas the second point is obtained exactly as in the proof of Proposition 3.12. \(\square \)
, whereas the second point is obtained exactly as in the proof of Proposition 3.12. \(\square \)
The following corollary is a simple consequence of Proposition 3.15:
Corollary 3.16
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there exists a positive constant \(C(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
Proof
Recall that
If \(1+\gamma \geqslant 0\), one notices that \(|v-v_{*}|^{1+\gamma } \leqslant 2^{\frac{1+\gamma }{2}}\langle v\rangle ^{1+\gamma }\langle v_{*}\rangle ^{1+\gamma }\), so that
since \(1+\gamma <2.\) Let us now investigate the case \(1+\gamma < 0.\) One splits the integral defining \(\varvec{b}[f(t)](v)\) according to \(|v-v_{*}| \leqslant 1\) and \(|v-v_{*}|>1\). One has then, thanks to Cauchy-Schwarz inequality,
Noticing that
is independent of v, one gets
for some universal positive constant \(C >0.\) We deduce then (3.41) from the conservation of mass and Proposition 3.15. \(\square \)
Estimate (3.41) implies of course that \({\sup _{t\geqslant 1}}\left| \varvec{b}[f(t)] \cdot v\right| \leqslant C(f_{\mathrm {in}})\,\langle v\rangle ^{\max (1,2+\gamma )}\). Additionally, we need the following estimate:
Lemma 3.17
Assume \(-2< \gamma <0\). There exist two constants \(c_{0},c_{1} >0\) depending only on \(\gamma \) such that, for any nonnegative \(g \in L^{1}_{2+\gamma }({\mathbb {R}}^{3})\)
where we recall that \(-\varvec{c}_{\gamma }[g](v)=2(\gamma +3)\int _{{\mathbb {R}}^{3}}|v-v_{*}|^{\gamma }g(v_{*})\mathrm {d}v_{*}\geqslant 0.\)
Proof
Let \(\delta >0\) be given. One writes
Since \(\left| \,|v|^{2}-|v_{*}|^{2}\right| \leqslant \frac{1}{2}|v-v_{*}|^{2}+\frac{1}{2}|v+v_{*}|^{2} \leqslant \frac{3}{2}|v-v_{*}|^{2}+4|v|^{2}\), we get
which gives the result using that
and recalling the definition of \(\varvec{c}_{\gamma }[g]\). \(\square \)
4 De Giorgi’s Approach to Pointwise Bounds
We introduce, as in [20], for any fixed \(\ell \in (0,\frac{1}{2\varvec{\varepsilon }})\),
To prove an \(L^{\infty }\) bound for f(t, v), one looks for an \(L^{2}\)-bound for \(f_{\ell }\). We start with the following estimate.
Lemma 4.1
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). There exist \(c_{0},C_{0} >0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\) and \(H(f_{\mathrm{in}})\) such that, for any \(\ell \in (0,\frac{1}{2\varvec{\varepsilon }})\),
Proof
Given \(\ell \in (0,\frac{1}{2\varvec{\varepsilon }})\), one has \(\partial _{t}\left( f_{\ell }^{+}\right) ^{2}=2f_{\ell }^{+}\partial _{t}f_{\ell }^{+}=2f_{\ell }^{+}\partial _{t}f\) and \(\nabla f_{\ell }^{+}={\mathbf {1}}_{\{f\geqslant \ell \}}\nabla f\), so that
Now, one easily checks that
Therefore,
Using that \(\tfrac{1}{2}-\varvec{\varepsilon }\ell >0\) and \(-\varvec{c}_{\gamma }[f] \geqslant 0\), we deduce from Proposition 2.3 and Proposition 1.8 with \(\phi =f_{\ell }^{+}\) and \(\delta >0\) small enough that there exist positive constants \(c_{0}, C_{0}\) depending on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
Notice that, using again inequality (3.13), we can replace easily the above with (4.1) with a different (but irrelevant) choice of \(c_{0},C_{0}\). \(\square \)
Inspired by De Giorgi’s iteration method introduced for elliptic Equations [16], the crucial point in the level set approach of [20] is to compare some suitable energy functional associated to \(f_{\ell }^{+}\) with the same energy functional at some different level \(f_{k}^{+}.\) The key observation here is that, if \(0 \leqslant k <\ell \), then
Indeed, on the set \(\{f_{\ell }\geqslant 0\}\), one has \(f \geqslant \ell >k\), so that \(f^{+}_{k}=f-k=f^{+}_{\ell }+(\ell -k)\) and \(\frac{f^{+}_{k}}{\ell -k}=\frac{f^{+}_{\ell }}{\ell -k}+1 \geqslant 1.\) In particular, for any \(\alpha \geqslant 0\), we deduce that
which, since \(f_{\ell }^{+}\leqslant f^{+}_{k}\), gives
On this basis, we need the following interpolation inequality where the dependence of \(f_{\ell }^{+}\) with respect to time is omitted hereafter:
Lemma 4.2
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). There exists \(C >0\) (independent of \(\varvec{\varepsilon }\) and \(f_{\mathrm{in}}\)) such that, for any \(0 \leqslant k < \ell \), one has
Moreover, for \(p \in [1,3)\), there is \(C_{p} >0\) such that,
Finally, for any \(q \in \left( \frac{8}{3},\frac{10}{3}\right) \), there is \(c_{q} >0\) such that
with \(s=-\frac{3\gamma }{10-3q} > -\frac{3}{2}\gamma \).
Proof
The proof is based on the interpolation inequality
with
Moreover, for the special case \(r_{1}=6\), \(r_{2}=2\), \(a_{1}=\frac{\gamma }{2}\) and \(r \in (2,6)\), thanks to Sobolev embedding, the identity will become
With these tools in had, one has for \(0 \leqslant k < \ell \) and \(r >2\), writing \(r=2+2\alpha \) with (4.2),
so that (4.7) gives, with \(a=\frac{\gamma }{r}\),
with \(\theta =\frac{3r-6}{2r}\) and \(a_{2}=\frac{\gamma }{2}\frac{10-3r}{6-r}\). One picks then \(r=\frac{10}{3}\) so that \(a_{2}=0\) and \(r\theta =2\), to obtain (4.3). One proceeds in the same way to estimate \(\Vert \langle \cdot \rangle ^{\gamma }f_{\ell }^{+}\Vert _{L^{p}}^{p}\). Namely, for \(r >p\),
and, with \(r >2p\), imposing in (4.7) \(a_{2}=0\) and \(a=\frac{\gamma \,p}{r}\), we get \(\theta =\frac{2p}{r}\) and
which gives (4.4) when \(r=2+\frac{4p}{3}\) (notice that \(r >2p\) since \(p <3\)).
Let us now prove (4.5). Let us consider first \(q >2\) and use (4.6). One has
with \(\theta _{i} \geqslant 0\) \((i=1,2,3)\) such that
Imposing \(q\theta _{3}=2\), this easily yields
Using Sobolev inequality, this gives, for any \(q \in \left( \frac{8}{3},\frac{10}{3}\right) \), the existence of a positive constant \(C >0\) such that
Using then (4.2), for any \(q >2\), one has \(\Vert f_{\ell }^{+}\Vert _{L^{2}}^{2} \leqslant (\ell -k)^{2-q}\,\Vert f_{k}^{+}\Vert _{L^{q}}^{q}\) for \(0 \leqslant k < \ell \), and the above inequality gives the result.\(\square \)
Let us now introduce, for any measurable \(f:=f(t,v) \geqslant 0\) and \(\ell \geqslant 0\), the energy functional
We have then the fundamental result for the implementation of the level set analysis.
Proposition 4.3
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, for any \(p_{\gamma } \in (1,3)\) and any \(s > \frac{3}{2}|\gamma |\), there exist some positive constants \( C_{1},C_{2}\) depending only on s, \(\Vert f_{\mathrm{in}}\Vert _{L^1_2}\) and \(H(f_{\mathrm{in}})\) such that, for any times \(0 \leqslant T_{1} < T_{2} \leqslant T_{3}\) and \(0 \leqslant k < \ell \),
Proof
Let us fix \(0 \leqslant T_{1} < T_{2} \leqslant T_{3}\). Integrating inequality (4.1) over \((t_{1},t_{2})\), we obtain that
Thus, if \(T_{1}\leqslant t_{1} \leqslant T_{2} \leqslant t_{2}\leqslant T_{3}\), one first notices that the above inequality implies that
and, taking the supremum over \(t_{2} \in [T_{2},T_{3}]\), one gets
Integrating now this inequality with respect to \(t_{1} \in [T_{1},T_{2}]\), one obtains
Therefore, applying Proposition 2.4 with \(\lambda =\gamma <0\), \(g=f\) and \(\varphi = f^{+}_{\ell }\), we see that
for \(p_{\gamma } >1\) such that \(-\gamma \,q_{\gamma } < 3\), where \(\frac{1}{p_{\gamma }}+\frac{1}{q_{\gamma }}=1.\) Notice that, since \(\gamma \in (-2,0)\), any \(p_{\gamma } \in (1,3)\) is admissible. We resort now to Lemma 4.2 to estimate the last three terms on the right-hand side of (4.9). Applying (4.3), one first has
Since
by definition of the energy functional, we get
for some positive constant \({\bar{C}}_{0}\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). Similarly, using (4.4) first with \(p=1\) and then with \(p=p_{\gamma }>1\), one deduces that
Regarding the first term in the right-hand side of (4.9), one uses (4.5) with \(q=\frac{10}{3}+\frac{\gamma }{s} \in \left( \frac{8}{3},\frac{10}{3}\right) \), where \(s >\frac{3}{2}|\gamma |\) is given, to get
for some positive constant \(\varvec{c}_{q} >0.\) Thus
Gathering (4.9)–(4.11)–(4.10)–(4.12) gives the result recalling that \(q=\frac{10}{3}+\frac{\gamma }{s}\). \(\square \)
Remark 4.4
Notice that, for \(-\frac{4}{3}< \gamma < 0\), then, one can choose \(s=2 > \frac{3}{2}|\gamma |\) in (4.8) to get \(\sup _{\tau \in [T_{1},T_{3}]}\varvec{m}_{s}(\tau )=\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\). For \(\gamma \leqslant -\frac{4}{3}\), we will rather use (4.8) with the choice \(s=3\).
With this, we can implement the level set iteration to deduce Theorem 1.10.
Proof of Theorem 1.10
We first start with short times, that is, we are concerned at this point with the appearance of the norm. In all the proof, \(C(f_{\mathrm {in}})\) will denote a generic constant depending only on \(f_{\mathrm {in}}\) through its \(L^{1}_{2}\)-norm and entropy \(H(f_{\mathrm{in}})\). Let us fix \(T>t_{*}>0\) and let \(K>0\) (to be chosen sufficiently large). We consider the sequence of levels and times
We apply Proposition 4.3 with \(T_{3}=T\) and the choices
to conclude that
that is,
for some positive constants \(C_{1},C_{2}\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) (but not on n), where
Notice that

so that Proposition 3.15 together with Corollary 3.10 ensure that
We look now for a choice of the parameters K and \(Q >0\) ensuring that the sequence \((E_{n}^{\star })_{n}\) defined by
satisfies (4.13) with the reversed inequality. Notice that
is equivalent to
We first choose Q in a such a way that all the terms \(\left[ \cdots \right] ^{n}\) are smaller than one, i.e.
where we recall that \({s>\frac{3}{2}|\gamma |}\) and \(p_{\gamma } <3.\) With such a choice, (4.14) would hold as soon as
This would hold for instance if each term of the sum is smaller than \(\frac{1}{3}\), and a direct computation shows that this amounts to choose
with
By a comparison principle (because \({E}_{0} ={E}^{\star }_{0}\)), one concludes that
and in particular, since \(Q >1\),
Since \(\lim _{n}t_{n}=t_{*}\) and \(\lim _{n}\ell _{n}=K\), this implies that
for \(K \geqslant K(t_{*},T)\) and, in particular,
Recall that \(K(t_{*},T)=\max \{K_{i}(t_{*},T),i=1,2,3,4\}\) as defined in (4.16). We estimate it roughly by the sum of these four terms, i.e.
and notice that the dependence with respect to \(T,t_{*}\) and t is encapsulated in the term \(E_{0}\) and \(K_{2}(t_{*},T)\) (through \(t_{*}^{-1}\) and \(\varvec{y}_{s}\)). One has easily
for some positive constants \(c_{2},c_{3} >0\) depending on \(Q,s,p_{\gamma }\) and \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}, H(f_{\mathrm{in}})\) (through \(C_{1},C_{2}\)).
Noticing that \(E_{0}\) is bounded away from zero (by some constant independent of \(t_{*},T\))Footnote 1 and that \({E}_0\leqslant C(f_{\mathrm {in}})\big (T-\frac{t_{*}}{2} + {t_{*}^{-\frac{3}{2}}}\big )\), since \({\frac{2s+3\gamma }{4s+3\gamma }} <\frac{1}{2}\), we can derive the estimate
for some positive constant C depending on \(Q,s,p_{\gamma }\) and the constants \(C_{1},C_{2}\) appearing in (4.16). Thus, taking \(0<t_{*}<T=2\), we obtain the result in the time interval (0, 2].
For \(T\geqslant 2\), we copycat the previous argument with the increasing sequence of times
In this case the first term in the right-hand side of (4.13) can be replaced with (since no dependence upon \(t_{*}\) appears)
Furthermore, \(\lim _{n}t_{n}=T-1\) and, by Corollary 3.10,
Consequently,
The result follows since \(T\geqslant 2\) is arbitrary. \(\square \)
A simple consequence of the above is the following:
Corollary 4.5
Assume that \(-\frac{4}{3}< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there is a constant \(C>0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that, for any \(t_{*} >0\),
In particular, there exists some explicit \(\varvec{\varepsilon }^{\dagger }\) and \(\kappa _{0}\) both depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that, for any \(\varvec{\varepsilon }\in [0,\varvec{\varepsilon }^{\dagger }]\),
Proof
The proof is a direct consequence of Theorem 1.10 (cf. also Remark 4.4) since, for \(-\frac{4}{3}< \gamma <0\), we can pick \(s=2\) and \(\sup _{t \in [0,T]}\varvec{m}_{s}(t)=\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) is independent of T. \(\square \)
5 Long-time Behaviour: Algebraic Convergence Result
We investigate now the long-time behaviour of solutions to (1.11.10). Our approach is based upon the entropy/entropy dissipation method.
5.1 General strategy and estimates
In this section, for any \(\eta \in {\mathbb {R}}\), we will denote by \({\mathscr {D}}_{\varvec{\varepsilon }}^{(\eta )}(g)\) the entropy production associated to the interaction kernel \(\Psi (z)=|z|^{\eta +2}\), i.e.
where \(\varvec{\** }_{\varvec{\varepsilon }}[g](v,v_{*})\) is defined by (2.5). We recall the following result from a previous contribution [15].
Theorem 5.1
Assume that \(0 \leqslant g \leqslant \varvec{\varepsilon }^{-1}\) is such that
and let
For any \(\eta \geqslant 0\),
where \(\lambda _{\eta }(g) >0\) is given by
with
and
Recall that \({\mathcal {M}}_{\varvec{\varepsilon }}\) and \(b_{\varvec{\varepsilon }}\) are introduced in Definition 1.1.
Our approach is based on the interpolation between the entropy production with parameter \(\gamma \) and the entropy production with parameter \(\eta \geqslant 0.\) Namely, for a given g satisfying (1.85.2), a simple consequence of Hölder’s inequality is that
or equivalently,
Noticing that \(1-\frac{\gamma }{\eta } >0\), we can invoke Theorem 5.1 to bound from below \({\mathscr {D}}_{\varvec{\varepsilon }}^{(0)}(g)\) in terms of \({\mathcal {H}}_{\varvec{\varepsilon }}(g|{\mathcal {M}}_{\varvec{\varepsilon }})\), and we need to deduce an upper bound for \({\mathscr {D}}_{\varvec{\varepsilon }}^{(\eta )}(g)\). We begin with the lower bound of \({\mathscr {D}}_{\varvec{\varepsilon }}^{(0)}(f(t))\) for solutions to (1.11.10), which can be deduced from Theorem 5.1.
Proposition 5.2
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there exist \(\varvec{\varepsilon }_{1} \in (0,\varvec{\varepsilon }_{0}]\) and a positive constant \({\bar{C}}_{1} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
where
Proof
From Theorem 5.1, there is some universal constant \(c >0\) such that
with
and
Here,
since
by conservation of energy and because \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}} \geqslant 1\). As shown in [15, Remarks 2.10 & 2.11], there is a positive constant \(C_{0} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\) such that \(\min \left( \frac{1}{B(t)},\frac{1}{\varvec{e}^{3}(t)}\right) \geqslant C_{0}\) for any \(t\geqslant 0.\) Therefore, there is a positive constant \({\bar{C}}_{0} >0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm {in}})\) such that
and, since \(\kappa _{0}(t) \leqslant 1\) and \(b_{\varvec{\varepsilon }} \geqslant \frac{1}{8}\) for \(\varvec{\varepsilon }\) small enough (see [2, Lemma A.1]), we easily deduce that
for any \(t\geqslant 0\) with \({\bar{C}}_{1}=\tfrac{1}{8}{\bar{C}}_{0}.\) Since \(\kappa _{0}(t)=1-\varvec{\varepsilon }\Vert f(t)\Vert _{L^{\infty }}\), one has \(\kappa _{0}(t) \geqslant 1-\varvec{\varepsilon }\chi (t)\) for any \(t\geqslant 0\) and (5.6) becomes
Expanding \((1-\varvec{\varepsilon }\chi (t))^{4}\) and noticing that \(-\varvec{\varepsilon }^{3}\chi ^{3}(t) \geqslant -\varvec{\varepsilon }^{2}\chi ^{2}(t) \geqslant -\varvec{\varepsilon }\chi (t)\) because \(\varvec{\varepsilon }\chi (t)\leqslant 1\), one gets the result. \(\square \)
We now derive an upper bound for \({\mathscr {D}}_{\varvec{\varepsilon }}^{(\eta )}(g)\). A first observation is the following technical estimate:
Lemma 5.3
For any \(0 \leqslant g \leqslant \varvec{\varepsilon }^{-1}\) satisfying (5.3) and any \(\eta \geqslant -2\), one has
where we recall that \(\kappa _{0}(g)=\inf _{v \in {\mathbb {R}}^{3}}\left( 1-\varvec{\varepsilon }g(v)\right) =1-\varvec{\varepsilon }\Vert g\Vert _{L^{\infty }}.\)
Proof
Using definition (2.5), one has
where \(h(v)=\log (g(v))-\log (1-\varvec{\varepsilon }g(v)).\) Using the obvious estimate
one has
Using the fact that \(|v-v_{*}|^{\eta +2} \leqslant 2^{\frac{\eta +2}{2}}\langle v\rangle ^{\eta +2}\langle v_{*}\rangle ^{\eta +2}\), we get the desired result thanks to (5.3). \(\square \)
On the basis of estimates (5.7) and (5.5), we need to provide a uniform in time upper bound of the above weighted Fisher information along solutions to (1.11.10). We follow the approach of [27] and begin with a technical Lemma:
Lemma 5.4
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, for any \(s >\frac{3}{2}\), there exists \(C_{s}(f_{\mathrm {in}}) >0\) depending on s, \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that, for any \(t\geqslant 0\) and \(k \geqslant 0\)

and

Proof
We use the following obvious estimate: for any \(p,r >1\), there is \(C_{p,r} >0\) such that
For notational simplicity, in several places we omit the dependence of f with respect to t. Splitting \(\varvec{c}_{\gamma }[f]\) as
one has that
Clearly,
so that
According to Cauchy-Schwarz inequality, for any \(s >\frac{3}{2}\)
and consequently

for some positive constant depending only on s and \(\Vert f_{\mathrm{in}}\Vert _{L^{1}}\). Using Hölder’s inequality,
and, according to Young’s convolution inequality,
where \(\left\| \,|\cdot |^{\gamma }{\mathbf {1}}_{|\cdot |\leqslant 1}\right\| _{L^{\frac{3}{2}}} < \infty \) since \(\frac{3}{2}\gamma +3>0\) (recall that \(\gamma \in (-2,0))\). Since
we deduce that

Now using Proposition 3.15, this proves (5.8). Now, by (5.10), one has
and, proceeding as above, one obtains (5.9). \(\square \)
We can state now the following Proposition which is inspired by [27]:
Proposition 5.5
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Let \(\eta \geqslant \gamma -2.\) Assume moreover that
Then, for any \(t_{0} >0\), there exists \(C >0\) depending on \(\eta ,t_{0}\) and on \(f_{\mathrm {in}}\) through \(\Vert f_{\mathrm {in}}\Vert _{L^1_{2{\eta +8-2\gamma }}}\) such that
In particular, for \(\eta \geqslant 0\), there is \(C_{\eta }(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\eta \) and such that
where we recall that \(\kappa _{0}(\tau )=1-\varvec{\varepsilon }\,\Vert f(\tau )\Vert _{L^{\infty }}\), \(\tau \geqslant 0.\)
Proof
Let \(\eta \geqslant \gamma -2\) be fixed. Since we aim to use Lemma 5.4, it will be convenient here to introduce \(k =\eta +2-\gamma \). We compute, as in [27, Proposition 1] the evolution of
for a solution \(f=f(t,v)\) to (1.11.10). To simplify notations, we write \(F=F(t,v)=f(1-\varvec{\varepsilon }f)\). One can check that
One computes, using that \(\log f \,\nabla f=\nabla \left[ f\log f-f\right] \), that
Similarly,
As in the proof of Lemma 3.8,
with \(\varvec{A}(v)=\langle v\rangle ^{2}\mathbf {Id}+(k-2)\,v\otimes v,\) whereas
resulting in
From (5.14), using the coercivity of \(\varvec{\Sigma }[f]\) and the fact that \(-\varvec{c}_{\gamma }[f] \geqslant 0\), we get
As in the proof of Proposition 3.9, we see that
and, since \(|\varvec{B}[f]\cdot v| \leqslant |\varvec{b}[f]\cdot v| +\varvec{\varepsilon }|\varvec{b}[f^2]\cdot v|\) with \(\varvec{\varepsilon }f^{2} \leqslant f\), one can check that \(\frac{1}{2}|\varvec{B}[f]\cdot v|\) also satisfies (3.44). We deduce then from (5.15) that there exists a constant \(C_{k}(f_{\mathrm {in}})>0\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and k, such that
Since
we have that
Using Lemma 5.4 with \(s=2\), we deduce then that, for any \(t_{0} >0\),

where we used Theorem 1.9 for the last estimate and where \(C_{k}(f_{\mathrm{in}})\) now depends on \(t_{0}\). Notice that, for \(s=2k+4 >4+|\gamma |\), Theorem 1.9 provides the growth of \(\varvec{m}_{2k+4}(t)\),  and \(\varvec{E}_{\frac{3k}{2}}(t)\) whenever \(\varvec{m}_{s}(0) < \infty \). Our assumption on \(f_{\mathrm{in}}\) exactly means that \(\varvec{m}_{2k+4}(0)< \infty .\) Integrating this inequality over \((t_{0},t)\) yields
and \(\varvec{E}_{\frac{3k}{2}}(t)\) whenever \(\varvec{m}_{s}(0) < \infty \). Our assumption on \(f_{\mathrm{in}}\) exactly means that \(\varvec{m}_{2k+4}(0)< \infty .\) Integrating this inequality over \((t_{0},t)\) yields
Clearly, \(S_{k}(t)\) has no sign but, according to [27, Eq. (B.3), Lemma B.4], for any \(\sigma >0\) there exists \(C_{\sigma } >0\) such that
yielding, for \(\sigma = 2\),
Let us note here that with our assumptions, one can deduce from (5.9) and Theorem 1.9 that \(S_{k}(t_{0})\) is actually finite. Indeed, (5.9) implies that \(S_{k}(t_{0}) < \infty \) if \(\varvec{m}_{2k+2r}(t_{0}) < \infty \) and  for some \(r > \frac{3}{2}\). According to Theorem 1.9, this holds if \(\varvec{m}_{{s}}(0) < \infty \) for \(s=2k+2r > 4-\gamma \). As already observed, one has \(\varvec{m}_{2k+2r}(0) < \infty \) with \(r=2 >\frac{3}{2}\). Recalling that \(k+\gamma =\eta +2\), this proves (5.11) with a positive constant C depending in particular on \(t_{0}\) (with \(C \lesssim t_{0}^{-2}\)). We deduce then (5.12) from (5.7) and (5.11). \(\square \)
for some \(r > \frac{3}{2}\). According to Theorem 1.9, this holds if \(\varvec{m}_{{s}}(0) < \infty \) for \(s=2k+2r > 4-\gamma \). As already observed, one has \(\varvec{m}_{2k+2r}(0) < \infty \) with \(r=2 >\frac{3}{2}\). Recalling that \(k+\gamma =\eta +2\), this proves (5.11) with a positive constant C depending in particular on \(t_{0}\) (with \(C \lesssim t_{0}^{-2}\)). We deduce then (5.12) from (5.7) and (5.11). \(\square \)
5.2 The case \(-\frac{4}{3}< \gamma < 0\)
We apply the result established here above to the case \(\gamma \in \left( -\frac{4}{3},0\right) \). In that case Proposition 5.2 can be stated as:
Proposition 5.6
Assume that \(-\frac{4}{3}< \gamma <0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there exists \(\varvec{\varepsilon }^{\star } \in (0,\varvec{\varepsilon }_{0}]\) and \({\bar{\lambda }}_{0} >0\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that, for \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }^{\star }]\),
Proof
The proof is a direct consequence of Proposition 5.2 and Corollary 4.5 since, recalling that \(\sup _{\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]}\Vert {\mathcal {M}}_{\varvec{\varepsilon }}\Vert _{L^{\infty }}<\infty \) by [2, Lemma A.1], one has
with \(C>0\) independent of \(\varvec{\varepsilon }\). Thus, there exists \(\varvec{\varepsilon }^{\star } \in (0,\varvec{\varepsilon }^{\dagger })\) such that \(\inf _{t\geqslant 1}\left( 1-98\varvec{\varepsilon }\chi (t)\right) > 0\) for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }^{\star }).\) \(\square \)
Remark 5.7
The restriction \(-\frac{4}{3}< \gamma <0\) is needed here only to ensure that \(\left( 1-98\varvec{\varepsilon }\chi (t)\right) > 0\). Thus, the above estimate (5.19) holds in any situation for which \( {\bar{\lambda }}_0={\bar{C}}_1 \inf _{t\geqslant 1}\left( 1-98\varvec{\varepsilon }\chi (t)\right) >0\).
This gives the following version of Theorem 1.7 where the assumptions on the initial datum are slightly relaxed with respect to the statement of Theorem 1.7:
Proposition 5.8
Let \(-\frac{4}{3}< \gamma < 0\). Let \(\eta >2 |\gamma |\) and \(0\leqslant f_{\mathrm {in}} \in L^{1}_{2\eta +8+2|\gamma |}({\mathbb {R}}^{3})\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, there exists \(C_{\eta }\) depending on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\eta >0\), and there exists \(\varvec{\varepsilon }^{\ddagger } \in (0,\varvec{\varepsilon }_{0}]\) such that for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }^{\ddagger })\),
As a consequence, given \(s > 2|\gamma |\), one has
provided that \(f_{\mathrm{in}} \in L^{1}_{r}\) with \(r > {\max (2s+8+2|\gamma |,\frac{s^{2}}{s-2|\gamma |})}\).
Proof
Using Proposition 5.6 and (5.5), for any \(\eta >0\),
For simplicity, we set
Since \(\dfrac{\mathrm {d}}{\mathrm {d}t}{\mathcal {H}}_{\varvec{\varepsilon }}(f(t)|{\mathcal {M}}_{\varvec{\varepsilon }})=-{\mathscr {D}}^{(\gamma )}_{\varvec{\varepsilon }}(f(t))\), one has
Integrating this inequality, we deduce that
i.e.
Let us estimate from below the integral of \(A_{\eta }(\tau )\). One has
where we used Jensen’s inequality and the convexity of the map** \(x >0 \mapsto x^{\frac{\gamma }{\eta }}.\) Therefore,
and, using (5.12), which holds since \(f_{\mathrm{in}} \in L^{1}_{2\eta + 8 - 2 \gamma }({\mathbb {R}}^{3})\), one gets
for some positive constant C depending on \(\eta ,\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) where we used (1.14) and the fact that \(\inf _{\tau \geqslant 1}\kappa _{0}(\tau ) >0\). Choosing \(\eta > -2\gamma \), this gives a decay rate
for all \(t\geqslant 2\) with \(C_{\eta }(f_{\mathrm{in}})\) depending on \(\eta ,\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). We conclude then with Csiszár-Kullback inequality for Fermi-Dirac relative entropy (2.2). Let us prove now the bound on \(\varvec{E}_{s}(t)\) for \(s \geqslant 0\). It follows from some standard arguments (see [28]). Namely, let \(s > -2\gamma \) be given and let \(p=\frac{s^{2}}{s+2\gamma } >s\). If \(f_{\mathrm{in}} \in L^{1}_{r}\) with \(r > \max (2s+8-2\gamma ,p)\), the bound (1.14) in Theorem 1.9 holds as well as the above (5.20) with \(\eta =s\). Then, for some positive \(C_{s}\) depending only on s, \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), \(H(f_{\mathrm{in}})\) and \(\varvec{m}_{r}(0)\), one has
for any \(t\geqslant 1\) (so that (5.20) holds). Using that \(\Vert {\mathcal {M}}_{\varvec{\varepsilon }}\Vert _{L^{1}_{s}}\) and \(\Vert {\mathcal {M}}_{\varvec{\varepsilon }}\Vert _{L^{1}_{p}}\) are bounded uniformly with respect to \(\varvec{\varepsilon }\) (see [2, Lemma A.1]), we deduce that there is \(c_{s} >0\) depending only on s, \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(\varvec{m}_{r}(0)\) and \(H(f_{\mathrm{in}})\) but not \(\varvec{\varepsilon }\) such that
Since \(-(1-\theta )\frac{s+2\gamma }{2|\gamma |}+\theta =0\), this proves that \(\sup _{t\geqslant 0}\varvec{m}_{s}(t) \leqslant 2c_{s}\). The proof is similar for the estimate of  where we notice that \(\max (p,\frac{2p-3\gamma }{4})=p\) which ensures the appearance of the \(L^{2}\)-moment
where we notice that \(\max (p,\frac{2p-3\gamma }{4})=p\) which ensures the appearance of the \(L^{2}\)-moment  thanks to Propositions 3.12 and 3.15. The result follows. \(\square \)
thanks to Propositions 3.12 and 3.15. The result follows. \(\square \)
5.3 Proof of Theorem 1.7: the case \(-2 < \gamma \leqslant -\frac{4}{3}\)
We are in position to give here the full proof of Theorem 1.7. It suffices to consider the case \(-2 < \gamma \leqslant -\frac{4}{3}\) since the case \(-\frac{4}{3}< \gamma < 0\) has been covered by Proposition 5.8 where in that result, \(\eta =\frac{1}{2}\left( s-8+2\gamma \right) \). With respect to the proof of Proposition 5.8, we no longer have a direct control of the norm \(\sup _{t\geqslant 1}\Vert f(t)\Vert _{\infty }\).
Recall that, according to Proposition 5.2, there is \({\bar{C}}_{1} >0\) depending on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) such that
with \(\chi (t)=\max \Big (\Vert f(t)\Vert _{L^{\infty }}\,,\,\sup _{\varvec{\varepsilon }>0}\Vert {\mathcal {M}}_{\varvec{\varepsilon }}\Vert _{L^{\infty }}\Big )\). Let us fix \(T>2\) and define
so that
Pick \(\varvec{\varepsilon }:=\varvec{\varepsilon }(T)\) such that
Note that the existence of such \(\varvec{\varepsilon }\) follows from Theorems 1.9 and 1.10, since \({s >\max (4-\gamma ,-\frac{3}{2}\gamma )}\) with our assumptions. The idea is to couple the a priori estimates with the entropy method to be able to conclude that in fact these quantities are independent of \(T>2\) as long as \(\varvec{\varepsilon }>0\) is less than some threshold depending only on the initial distribution \(f_{\mathrm {in}}\). The interpretation of this condition is that the initial distribution is not too saturated for the argument to hold. It is an open problem to prove that the relaxation to thermal equilibrium happens with a specific rate when \(f_{\mathrm {in}}\) is very close to a saturated state even in the hard potential case, see [2].
As in the proof of Proposition 5.8, we write
Recall that we assume here that \(f_{\mathrm{in}} \in L^{1}_{s}({\mathbb {R}}^{3})\) with \(s > 14+6|\gamma |.\) For notational simplicity, we write \(s=2\eta +8-2\gamma \) with \(\eta > 3+2|\gamma |.\) In all the sequel, we have then
Using (5.5), for such a choice of \(\eta \), we deduce from (5.21) that
Recalling that \(\dfrac{\mathrm {d}}{\mathrm {d}t}\varvec{y}(t)=-{\mathscr {D}}_{\varvec{\varepsilon }}^{(\gamma )}(f(t))\), we deduce after integration of the above inequality that
where we set \({\bar{C}}(\gamma ,\eta )=\frac{|\gamma |}{\eta }{\bar{C}}_{1}^{1-\frac{\gamma }{\eta }}\). Similar to the proof of Proposition 5.8, using the convexity of the map** \(r >0 \mapsto r^{\frac{\gamma }{\eta }}\), we have
Therefore, in light of (5.12) and using (5.22), there exists \(C_{\eta } >0\) depending only on \(f_{\mathrm {in}}\) such that
where we used (1.14) and the fact that \(\kappa _{0}(t) \geqslant 1-\varvec{\varepsilon }\chi ^{\star }\) for any \(t \in [1,T)\). Inserting this into (5.23),
for some positive constant \(C_{\gamma ,\eta } >0\) depending only on \(\eta ,\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). In other words
for any \(t \in (1,T)\). In particular
We use this last estimate to sharpen the control of the third moment of f(t, v).
Lemma 5.9
For \(\eta > 3+2|\gamma |\), one has
Proof
We use ideas similar to those introduced at the end of Proposition 5.8. For \(\eta >3+2|\gamma |\), observe that
where, in the last inequality, we used one side of the Csiszár-Kullback inequality (2.2). Let us note that \(C_{\eta }\) does not depend on \(\varvec{\varepsilon }\) since \(\Vert {\mathcal {M}}_{\varvec{\varepsilon }} \Vert _{L^{1}_{\eta }}\) is uniformly bounded thanks to [2, Lemma A.7]. Plugging into the aforementioned estimation for \(\varvec{y}(t)={\mathcal {H}}_{\varvec{\varepsilon }}(f(t)|{\mathcal {M}}_{\varvec{\varepsilon }})\), we obtain
Since \(\eta > 3+2|\gamma |\), the function
is bounded by some positive constant \(C_{\eta ,\gamma }\). We obtain then (5.25). \(\square \)
A simple consequence of the aforementioned Lemma is the following estimate on \(\chi ^{\star }\).
Lemma 5.10
Assume that \(\eta >3+2|\gamma |\), then there is a constant \( C_{1}:=C_{1}(\gamma ,\eta ,f_{\mathrm{in}})\) independent of \(\varvec{\varepsilon }\) and T such that
Proof
Using Theorem 1.10 (with \(s=3\)) and the fact that \(\sup _{\tau \in [0,2) }\varvec{m}_{3}(\tau ) \leqslant C(f_{\mathrm {in}})\) thanks to Proposition 3.11 (recall that (5.22) holds) we can use the previous estimate to conclude that
which, with (5.25), gives
where we used that \(1-\varvec{\varepsilon }\chi ^{\star } \leqslant 1\). This gives (5.26). \(\square \)
We introduce the map**
One has
We define
where \(M >0\) is a (large) constant to be determined. We consider values \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }]\) which ensure in particular that \(M < \phi ({\bar{x}}).\) Now, in such a case, the equation \(\phi (x)=M\) has two roots \(x_{1}<{\bar{x}}<x_{2}\) in the interval \((0,\varvec{\varepsilon }^{-1})\). In particular, \(\phi (x_{1})=M\) implies
Therefore, the inequality \(\phi (x) < M\) holds in the following two cases:
Let us now show that, choosing M large enough, the second case (ii) is an impossibility.
Lemma 5.11
Besides (5.27), assume that \(M\geqslant C_{1}\) and
Then, for \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star })\), it holds that
Proof
Notice that (5.29) means that \(\varvec{\varepsilon }_{\star } \leqslant \frac{1}{\chi ^\star (3)(1+\alpha )}.\) Applying Theorem 1.10 with \(s=3\) on the interval [1, 3), one has
for some positive C depending on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\) and this last quantity is finite and independent of \(\varvec{\varepsilon }\) thanks to Proposition 3.11 since \(\varvec{m}_{3}(0) <\infty .\) Therefore,
depends only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). Under the additional constraint (5.29), we observe that for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }]\) it holds \({\bar{x}}\geqslant \chi ^{\star }(3)\), which excludes the case (ii). By the aforementioned binary option, one gets the desired conclusion. \(\square \)
This argument shows the existence of a trap** region which can be extended to any \(T>3\).
Lemma 5.12
Assume (5.27) and (5.29) are in force. Then, defining
one can choose M large enough (explicit) such that \(T^{\star }=\infty \) for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star })\).
Proof
We already saw in Lemma 5.11 that \(T^{\star }\geqslant 3\). We argue by contradiction considering that \(T^{\star }<\infty \). In all the sequel, we will denote by u(t) a function of \(t \geqslant 0\) which is such that \(\lim _{t\rightarrow 0^{+}}u(t)=0\) (i.e. \(u(t)=o(1)\)) and that may change from line to line. Recalling and integrating the moment inequality (3.10) (with \(\delta =1\) and \(s=3\)) in the time interval \((T^\star ,T^\star +t )\), it follows that

since the latter three terms in the right-hand side can be made as small as desired when \(t \rightarrow 0\). In other words,
Using Theorem 1.10 applied on the interval \([1,T^\star + t )\), the fact that \(\sup _{\tau \in [0,2) }\varvec{m}_{3}(\tau ) \leqslant C(f_{\mathrm {in}})\,,\) and the continuous growth of the third moment (5.30), one is led to
for some positive C depending on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\) and \(H(f_{\mathrm{in}})\). Consequently, one can use (5.25) with \(T=T^\star \) to get
We deduce from this that there is some \({\overline{C}} >0\) independent of \(\varvec{\varepsilon }\) and M such that
where we used again that \(1-\varvec{\varepsilon }\chi ^{\star }(T^{\star }) \leqslant 1.\) Notice that, by definition of \(T^{\star }\),
where \( {1-\varvec{\varepsilon }\chi ^{\star }(T^{\star }) \geqslant } 1-\varvec{\varepsilon }x_{1} \geqslant 1-\varvec{\varepsilon }_{\star }x_{1}>\tfrac{1}{2}\). Thus, \(\left( 1-\varvec{\varepsilon }\chi ^{\star }(T^{\star })\right) ^{-\alpha } \in [1,2^{\alpha }]\) and, for t small enough, (5.31) implies that
Now set
One deduces from (5.32) that
which is a contradiction since, by definition of \(T^{\star }\), \(\chi ^{\star }(T^{\star }+t ) > x_{1}.\) Thus, for the above choice of M, we must have that \(T^{\star }=\infty \).\(\square \)
We have all in hands to conclude.
Proof of Theorem 1.7
The previous Lemma exactly means that, for some explicit \(\varvec{\varepsilon }_{\star } >0\) (associated to the above choice of M), one has
This proves in particular that
which is independent of \(\varvec{\varepsilon }\). This gives the no saturation property
At this stage, we can resume the proof of Proposition 5.8 to get the desired result. \(\square \)
6 Upgrading the Convergence
We explain in this section how the rate of convergence can be upgraded to a stretched exponential rate whenever the initial datum satisfies a more stringent decay in terms of large velocities decay. As before, our strategy is based upon suitable interpolations. Notations are those of Section 5.1 and we follow at first the interpolation procedure developed in [29, Section 5]. Namely, we begin by improving the interpolation inequality between \({\mathscr {D}}_{\varvec{\varepsilon }}^{(\gamma )}\) and \({\mathscr {D}}_{\varvec{\varepsilon }}^{(0)}\) provided by inequality (5.5).
Lemma 6.1
For a given \(a>0\) and \(q >0\) define, for any \(0 \leqslant g \leqslant \varvec{\varepsilon }^{-1}\),
where \(\varvec{\** }_{\varvec{\varepsilon }}\) is defined by formula (2.5). Then for any \(\gamma <0\) one has that
where \({\mathscr {D}}_{\varvec{\varepsilon }}^{(\gamma )}(g)\) is defined by formula (5.1).
Proof
For a given \(R>0\), we set \({\mathcal {Z}}_{a,R}{=}\left\{ (v,v_{*}) \in {\mathbb {R}}^{3}\times {\mathbb {R}}^{3};|v-v_{*}| \leqslant \left( \frac{R}{a}\right) ^{\frac{1}{q}}\right\} \) and denote by \({\mathcal {Z}}_{a,R}^{c}\) its complementary in \({\mathbb {R}}^{6}.\) We see that
We also notice that for any \(a,q>0\), we have that \(1\leqslant \exp \left( a|v-v_{*}|^q\right) \), and therefore \(2{\mathscr {D}}_{\varvec{\varepsilon }}^{(0)}(g) \leqslant \Gamma ^{a,q}_{\varvec{\varepsilon }}(g)\). Thus, the choice
is possible, and yields
which completes the proof. \(\square \)
Remark 6.2
Applying this inequality to a weak solution f(t, v) to (1.11.10) and assuming that the initial datum \(f_{\mathrm {in}}\) and \(\varvec{\varepsilon }>0\) are such that (5.19) holds, together with the estimate
we expect that the relative entropy
satisfies a differential inequality of the type
leading to an estimate like
for some positive constant \(A,B >0\). We will see that, even if we cannot prove directly (6.2), the (at most) slowly increasing growth of \(\Gamma _{\varvec{\varepsilon }}^{(a,q)}(f(t))\) will be such that the above decay still holds.
Following the paths of Section 5, we first look for suitable upper bound for \(\Gamma _{\varvec{\varepsilon }}^{(a,q)}(g).\) We proceed as in Lemma 5.3 to get the following result.
Lemma 6.3
For any \(0 \leqslant g \leqslant \varvec{\varepsilon }^{-1}\) satisfying (5.3) and any \(a>0\), \(q \in (0,1)\) one has
where
Proof
Recalling definition (2.5), we see that
where \(h(v)=\log (g(v))-\log (1-\varvec{\varepsilon }g(v))\) and \(F=g(1-\varvec{\varepsilon }g)\). Using the obvious estimate
and \(|v-v_{*}|^{2}\exp (a|v-v_{*}|^{q}) \leqslant 2\langle v\rangle ^{2}\mu _{a,q}(v)\langle v_{*}\rangle ^{2}\mu _{a,q}(v_{*})\) since \(q \in (0,1)\), one deduces that
This yields the result. \(\square \)
As for Proposition 5.5, on the basis of (6.3) and (6.1), it is useful to get a uniform in time upper bound of the above Fisher information with exponential weights along solutions to (1.11.10). Before doing so, let us introduce the following objects:
Definition 6.4
Given \(a,q >0\), we recall definition (6.4). Then, for any nonnegative measure function \(g\,:\,{\mathbb {R}}^{3}\rightarrow {\mathbb {R}}\), we set
Given \(s \geqslant 0\), we also introduce
If f(t, v) is a weak-solution to (1.11.10), we will moreover simply write
with similar notations for \({\overline{\Upsilon }}_{a,q,s}(t),{\overline{\vartheta }}_{a,q,s}(t)\). We also set
Estimates on the evolution of the above family of moments are easily deduced from Theorem 1.9 since we keep track, for the evolution of \(\varvec{E}_{s}(t)\), of the dependency with respect to s. Namely, one has the following proposition, with a proof quite similar to that of [22, Corollary 4.1].
Proposition 6.5
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Let \(a >0\) and \(0< q <\frac{4+2\gamma }{8-\gamma }\). Assume that
Then there exists \(\varvec{C}_{a,q} >0\) depending only on a, q and \(f_{\mathrm{in}}\) such that
Proof
As in [22, Corollary 4.1], we notice that
so that thanks to Theorem 1.9
Consequently, in order to prove the result, we just need to show that the sum is finite. Using now (1.15), there is \(\beta _{1} >0\) such that
Clearly, for n large enough \((1+nq)^{\frac{5}{2}} \leqslant c_{0}2^{nq}\) for some universal \(c_{0} >0\), so that
with \(b=\frac{8-\gamma }{4+2\gamma }q\) and \(\ell = \frac{8-\gamma }{4+2\gamma } (\gamma -2)+1.\) Using Stirling formula and d’Alembert’s ratio test, one sees easily that, if \(b <1\), then the sum
whereas
This proves the result.\(\square \)
Remark 6.6
From the above proof, one sees that, if \(q= {\frac{4+2\gamma }{8-\gamma }}\), then the above result still holds if \(2^{\frac{q}{4}}a\beta _{1}q e <1\).
We need in the sequel an analogue of Lemma 5.4.
Lemma 6.7
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Then, given \(a,q >0\) and any \(s >\frac{3}{2}\), there exists \(C_{s}(f_{\mathrm {in}}) >0\) depending on s, \(f_{\mathrm{in}}\), (but not on a, q) such that, for any \(k \geqslant 0\) and any \(t\geqslant 0\),
and
Proof
The proof is very similar to that of Lemma 5.4 and is based upon (5.10). We use the same notations as in Lemma 5.4 and use the splitting \(\varvec{c}_{\gamma }[f]=\varvec{c}_{\gamma }^{(1)}[f]+\varvec{c}_{\gamma }^{(2)}[f]\). One has
As in Lemma 5.4, a simple use of Cauchy-Schwarz inequality yields, for any \(s > \frac{3}{2}\),
for some positive constant depending only on \(s, \Vert f_{\mathrm {in}}\Vert _{L^1_{2}} \). In the same way, as in Lemma 5.4, we deduce from Hölder’s inequality, and Proposition 3.15 that

This proves (6.5). Now, the proof of (6.6) follows the same lines as that of (5.9). \(\square \)
Proposition 6.8
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Let \(b,q >0\) be given, with \(q < {\frac{4+2\gamma }{8-\gamma }}\). Assume moreover that
for some \(\delta >0\). Then, for any \(t_{0} >0\), there exists \(C >0\) depending on \(b,\delta ,q,t_{0}\) and \(f_{\mathrm{in}}\), such that
Proof
Let us fix \(b,q >0\). We investigate the evolution of
for a solution \(f=f(t,v)\) to (1.11.10). To simplify notations, we write \(F=F(t,v)=f(1-\varvec{\varepsilon }f)\). One checks, similar to (5.13), that
with
and
For the latter, we notice that
with \(\varvec{A}_{\mu }(v)=\langle v\rangle ^{2}\mathbf {Id}+\left[ (q-2)+b\,q\,\langle v\rangle ^{q}\right] \,v\otimes v\).
As in the proof of Proposition 5.5, using that both \(|\varvec{b}[f]\cdot v|\) and \(\frac{1}{2}|\varvec{B}[f]\cdot v|\) satisfy (3.44), and using now that
one deduces the following analogue of (5.165.18),
for some positive constant \(C_{b,q}(f_{\mathrm {in}})\) depending on b, q and \(f_{\mathrm {in}}\) only through \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\). We use now the results of Lemma 6.7 to get for \(s=2\) that
where \(r=\max (2q+\gamma ,q)\). For any \(\delta >0\) and \(t_{0} >0\), since \({\overline{\vartheta }}_{2b,q,2r+4}(t) \leqslant C_{\delta }\,{\vartheta }_{2b+\delta ,q}(t)\) and similarly for \({\overline{\Upsilon }}_{b,q,r}(t)\) and the remainder terms, one has that, for \(t\geqslant t_0\),
Using now Proposition 6.5, assuming that \(q < \frac{4+2\gamma }{8-\gamma }\) and \( {\vartheta }_{2{\tilde{b}}+\delta ,q}(0) < \infty \) (after renaming \(\delta >0\)) we deduce that for \(t\geqslant t_0\) and \(\delta >0\),
for some positive constant \(C_{\delta ,b,q,t_{0}}(f_{\mathrm {in}})\) depending only on \(\delta ,b,q,t_{0}\) and \(f_{\mathrm {in}}\). Integrating this inequality over \((t_{0},t)\) yields
Arguing as in the proof of [27, Eq. (B.3), Lemma B.4], introducing \(A=\{v \in {\mathbb {R}}^{3}\;;\;f(t,v) <1\}\), one checks easily that
Introducing then \(B:=\{v \in {\mathbb {R}}^{3}\;;\;f(t,v)\geqslant \exp \left( -{3}\,b\langle v\rangle ^{q}\right) \}\), one splits the integral over A into the integral over \(A \cap B\) and \(A \cap B^{c}\). On the one hand, for \(v \in A \cap B\), \(\log \frac{1}{f(t,v)} \leqslant {3}\,b\langle v\rangle ^{q}\) and, for any \(\delta >0\), there exists \(C_{\delta }=C(\delta ,q,b) >0\) such that
On the other hand, for \(v \in A\cap B^{c}\), using that \(x\log \frac{1}{x} \leqslant \frac{2}{e}\sqrt{x}\), one has
so that
This shows that, for any \(\delta >0\),
Moreover, we deduce from Eq. (6.6) in Lemma 6.7 together with Proposition 6.5 that \(\varvec{S}_{b,q}( {t_0})\) is finite under our assumption on \(f_{\mathrm{in}}\) and
for some finite \(C >0\) depending on \(b,q,\delta , {t_0} >0\) and \(f_{\mathrm {in}}\). \(\square \)
We deduce from this the following estimate for \(\Gamma _{\varvec{\varepsilon }}^{(a,q)}(f(t))\).
Corollary 6.9
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Let \(a >0\) and \(0<q <{\frac{4+2\gamma }{8-\gamma }}\), and assume that for some \(\delta >0\),
Then, there exists \(C_{\delta ,a,q}(f_{\mathrm {in}})>0\) depending only on \(\delta ,a,q\) and \(f_{\mathrm {in}}\) such that
where we recall that \(\kappa _{0}(\tau )=1-\varvec{\varepsilon }\,\Vert f(\tau )\Vert _{L^{\infty }}\), \(\tau \geqslant 0.\)
Proof
The proof follows from Lemma 6.3, Proposition 6.8 with \(b=a\), and the fact that \(\langle v\rangle ^{2}\mu _{a,q}(v) \leqslant {C_{\delta ,q}} {\langle v\rangle ^{\gamma }}\mu _{a+\delta ,q}(v)\) for any \(\delta >0\). \(\square \)
Theorem 6.10
Assume that \(-2< \gamma < 0\) and let a nonnegative initial datum \(f_{\mathrm {in}}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\) be given. For \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\), let \(f(t,\cdot )\) be a weak-solution to (1.11.10). Let \(a_0 >0\) and \(0<q <{\frac{4+2\gamma }{8-\gamma }}\), and assume that
Then, there exists some explicit \(\lambda >0\) depending only on \(a_0,q\) and \(f_{\mathrm{in}}\) such that, for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star })\) (where \(\varvec{\varepsilon }_{\star }\) is prescribed by Theorem 1.7),
As a consequence,
Proof
We first observe that, thanks to Theorem 1.7 and under the assumptions on the initial datum \(f_{\mathrm {in}}\), there is \(\varvec{\varepsilon }_{\star } \in (0,\varvec{\varepsilon }_{0}]\) depending only on \(f_{\mathrm {in}}\) such that for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star }]\),
Let us write
One uses then (6.1) and (5.19) which, by Proposition 5.2 and Theorem 1.7, actually holds for \(-2<\gamma <0\). We first deduce that, for \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{\star })\), \(t \geqslant 1\), and \(a >0\), \(q \in (0,1)\),
where we recall that we already know that \(\frac{\Gamma _{\varvec{\varepsilon }}^{(a,q)}(f(t))}{{\mathscr {D}}_{\varvec{\varepsilon }}^{(0)}(f(t))} >1\), so that \( \Gamma _{\varvec{\varepsilon }}^{(a,q)}(f(t)) \geqslant {{\bar{\lambda }}_{0}\, \varvec{y}(t)} \). We deduce then that
Using Grönwall’s Lemma, we get
We introduce
so that
Assume now that there is \(t_{0} >2\) and some \(m {>} 0\) such that
Then, since \( \tau \mapsto \varvec{y}(\tau )\) is non increasing, one has
and
Using now that, for any \(\alpha \in {\mathbb {R}},\) the function \(r >\exp (-\alpha ) \mapsto (\alpha +\log r)^{\frac{\gamma }{q}}\) is convex, and applying it with \(\alpha =-\log {\bar{\lambda }}_{0}+t_{0}^{m}\), we deduce from Jensen’s inequality that
Using Corollary 6.9 together with Proposition 6.5, choosing parameters \(a,\delta >0\) such that \(a_0=\Big (2a+\delta \Big ){ 2^{\frac{q(1+|\gamma |)}{|\gamma |}}}\), there are positive constants \(C_{0},C_{1}>0\) (independent of \(t_{0}\)) such that
so that
Consequently, there exists \(C_{2} >0\) such that
Inserting this in (6.10), we now deduce that
Since we proved that assumption (6.11) implies estimate (6.12), we see that for any \(t >2\) and any \(m {>} 0\), we have the following alternative:
-
(i)
either \(\;\;\varvec{y}(t) \leqslant \exp \left( -\left( \frac{t}{2}\right) ^{m}\right) \),
-
(ii)
or \(\;\;\varvec{y}(t) \leqslant \varvec{y}(1)\exp \left( -\frac{{\bar{\lambda }}_{0}C_{2}}{2a^{\frac{\gamma }{q}}}\,t^{1+m\frac{\gamma }{q}}\right) \).
At this state, choosing \(m >0\) so that \(m=1+m\frac{\gamma }{q}\) (that is \(m=\frac{q}{q-\gamma }\)), we see that
for some explicit \(c_{a}:=\min \left( 2^{-m},\frac{{\bar{\lambda }}_{0}C_{2}}{2a^{\frac{\gamma }{q}}}\right) .\) This concludes the proof. \(\square \)
Change history
31 July 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
Indeed, for any \(t \geqslant 0\) and any \(R >0\), a simple use of Cauchy-Schwarz inequality yields

where |B(0, R)| is the volume of the euclidean ball centred in 0 and radius \(R >0.\) Since moreover \(\int _{|v|\geqslant R}f(t,v)\,\mathrm {d}v \leqslant R^{-2}\int _{{\mathbb {R}}^{3}}f(t,v)|v|^{2}\,\mathrm {d}v=3R^{-2}\) one sees that, picking \(R >0\) large enough,
 for any \(t \geqslant 0\). In turn, \(E_{0}>\tfrac{1}{2}c_{R} >0\).
for any \(t \geqslant 0\). In turn, \(E_{0}>\tfrac{1}{2}c_{R} >0\).
References
Chapman, S., Cowling, T.G.: The mathematical theory of non-uniform gases. Cambridge University Press, Cambridge (1970)
Alonso, R., Bagland, V., Lods, B.: Long time dynamics for the Landau-Fermi-Dirac equation with hard potentials. J. Differ. Equ. 270, 596–663, 2021
Bobylev, A.V., Pulvirenti, M., Saffirio, C.: From particle systems to the Landau equation: a consistency result. Comm. Math. Phys. 319, 683–702, 2013
Alexandre, R., Villani, C.: On the Landau approximation in plasma physics. Ann. Inst. H. Poincaré Anal. Non Linéaire 21, 61–95, 2004
Desvillettes, L.: On asymptotics of the Boltzmann equation when the collisions become grazing. Transp. Theor. Stat. Phys. 21, 259–276, 1992
Villani, C.: A review of mathematical topics in collisional kinetic theory, handbook of mathematical fluid dynamics, vol. I, pp. 71–305. North-Holland, Amsterdam (2002)
Desvillettes, L., Villani, C.: On the spatially homogeneous Landau equation for hard potentials. Part I : existence, uniqueness and smoothness. Commun. Partial Differ. Equ. 25, 179–259, 2000
Wu, K.-C.: Global in time estimates for the spatially homogeneous Landau equation with soft potentials. J. Funct. Anal. 266, 3134–3155, 2014
Desvillettes, L.: Entropy dissipation estimates for the Landau equation in the Coulomb case and applications. J. Funct. Anal. 269, 1359–1403, 2015
Golding, W., Gualdani, M.P., Zamponi, N.: Existence of smooth solutions to the Landau-Fermi-Dirac equation with Coulomb potential, preprint, arxiv: 2107.10463, 2021
Lu, X.: On spatially homogeneous solutions of a modified Boltzmann equation for Fermi-Dirac particles. J. Stat. Phys. 105, 353–388, 2001
Bagland, V.: Well-posedness for the spatially homogeneous Landau-Fermi-Dirac equation for hard potentials. Proc. R. Soc. Edinb. Sect. A 66, 415–447, 2004
Gualdani, M.-P., Guillen, N.: On \(A_{p}\) weights and the Landau equation. Calc. Var. Partial Differ. Equ. 58, 55, 2019
Beckner, W.: Pitt’s inequality with sharp convolution estimates. Proc. Am. Math. Soc. 136, 1871–1885, 2008
Alonso, R., Bagland, V., Desvillettes, L., Lods, B.: About the use of Entropy dissipation for the Landau-Fermi-Dirac equation. J. Stat. Phys. 183, 1–27, 2021
De Giorgi, E.: Sulla differenziabilità e l’analiticità delle estremali degli integrali multipli regolari. Mem. Accad. Sci. Torino. Cl. Sci. Fis. Mat. Nat. (3) 3, 25–43, 1957
Caffarelli, L., Chan, C.H., Vasseur, A.F.: Regularity theory for parabolic nonlinear integral operators. J. Am. Math. Soc. 24, 849–869, 2011
Vasseur, A.F.: The De Giorgi method for elliptic and parabolic equations and some applications. In: Lectures on the analysis of nonlinear partial differential equations, Part 4, 195–222, Morningside Lect. Math., 4, Int. Press, Somerville, MA, 2016.
Golse, F., Imbert, C., Mouhot, C., Vasseur, A.F.: Harnack inequality for kinetic Fokker-Planck equations with rough coefficients and application to the Landau equation. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 19, 253–295, 2019
Alonso, R.: Emergence of exponentially weighted \(L^{p}\)-norms and Sobolev regularity for the Boltzmann equation. Commun. Partial Differ. Equ. 44, 416–446, 2019
Alonso, R., Morimoto, Y., Sun, W., Yang, T.: De Giorgi argument for weighted \(L^2\cap L^{\infty }\) solutions to the non-cutoff Boltzmann equation, ar**v:2010.10065
Carrapatoso, K., Desvillettes, L., He, L.: Estimates for the large time behavior of the Landau equation in the Coulomb case. Arch. Ration. Mech. Anal. 224, 381–420, 2017
Lu, X., Wennberg, B.: On stability and strong convergence for the spatially homogeneous Boltzmann equation for Fermi-Dirac particles. Arch. Ration. Mech. Anal. 168, 1–34, 2003
Alexandre, R., Liao, J., Lin, C.-J.: Some a priori estimates for the homogeneous Landau equation with soft potentials. Kinet. Relat. Models 8, 617–650, 2015
Alexandre, R., Morimoto, Y., Ukai, S., Xu, C.-J., Yang, T.: Smoothing effect of weak solutions for the spatially homogeneous Boltzmann equation without angular cutoff. Kyoto J. Math. 52, 433–463, 2012
Desvillettes, L.: Entropy dissipation estimates for the Landau equation: general cross sections. In: From particle systems to partial differential equations. III, pp. 121–143. Springer Proc. Math. Stat., 162, Springer, 2016.
Alonso, R., Bagland, V., Lods, B.: Uniform estimates on the Fisher information for solutions to Boltzmann and Landau equations. Kinet. Relat. Models 12, 1163–1183, 2019
Desvillettes, L., Mouhot, C.: Large time behavior of the a priori bounds for the solutions to the spatially homogeneous Boltzmann equations with soft potentials. Asymptot. Anal. 54, 235–245, 2007
Cañizo, J., Einav, A., Lods, B.: On the rate of convergence to equilibrium for the linear Boltzmann equation with soft potentials. J. Math. Anal. Appl. 462, 801–839, 2018
Ladyzenskaja, O.A., Solonnikov, V.V., Ural’ceva, N.N.: Linear and quasilinear equations of parabolic type. American Mathematical Society, Providence (1968)
Simon, J.: Compact sets in the space \(L^p(0, T;B)\). Ann. Mat. Pura Appl. 146, 65–96, 1987
Temam, R.: Navier-stokes equations. Theory and numerical analysis. North Holland, Amsterdam (1977)
Cameron, S., Silvestre, L., Snelson, S.: Global a priori estimates for the inhomogeneous Landau equation with moderately soft potentials. Ann. Inst. H. Poincaré Anal. Non Linéaire 35, 625–642, 2018
Carrapatoso, K.: On the rate of convergence to equilibrium for the homogeneous Landau equation with soft potentials. J. Math. Pures Appl. 104, 276–310, 2015
Desvillettes, L., Villani, C.: On the spatially homogeneous Landau equation for hard potentials. Part II : H theorem and applications. Commun. Partial Differ. Equ. 25, 261–298, 2000
Acknowledgements
R. Alonso gratefully acknowledges the support from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant Bolsa de Produtividade em Pesquisa (303325/2019-4). B. Lods gratefully acknowledges the financial support from the Italian Ministry of Education, University and Research (MIUR), “Dipartimenti di Eccellenza” grant 2018-2022 as well as the support from the de Castro Statistics Initiative, Collegio Carlo Alberto (Torino). R. Alonso, V. Bagland and B. Lods would like to acknowledge the support of the Hausdorff Institute for Mathematics where this work started during their stay at the 2019 Junior Trimester Program on Kinetic Theory. Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Funding
Open access funding provided by Università degli Studi di Torino within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Mouhot.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Regularity estimates
We collect here several a priori regularity estimates for the solutions to (1.11.10). Clearly, it is possible to interpolate between \(L^{1}\) and \(L^{\infty }\) thanks to Theorem 1.10 to obtain a control on the \(L^{p}\)-norms with \(1<p<\infty \). We adopt another approach here which consists in directly investigating the evolution of the \(L^{p}\)-norms:
Proposition A.1
Assume that \(-2<\gamma <0\). Let \(p\geqslant 1\) and \(f_{\mathrm {in}}\in L^p({\mathbb {R}}^{3}) \cap L^{2}({\mathbb {R}}^{3})\cap L^1_{\varvec{z}_{p}}({\mathbb {R}}^{3}) \) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\), with
Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and let f(t, v) be a weak solution to (1.11.10). Then, there exists some constant \(C_p(f_{\mathrm {in}})\) depending on p and \(f_{\mathrm {in}}\) such that, for every \(T>0\),
Proof
We start with the formulation (1.11.10)
For \(p \geqslant 1\), multiplying this identity with \(f^{p-1}(t,v)\) and integrating over \({\mathbb {R}}^{3}\), one deduces
Using the coercivity estimate in Proposition 2.3, \(|F| \leqslant f\), and noticing that \(f^{\frac{p}{2}}\nabla f^{\frac{p}{2}}=\frac{p}{2}f^{p-1}\nabla f\), we obtain, after integration between 0 and T,
Note that from this point on, the estimates do not use \(\varvec{\varepsilon }\) and are thus similar to that of the usual Landau equation. Since \(f^{p-2}|\nabla f|^{2}=\frac{4}{p^{2}}|\nabla f^{\frac{p}{2}}|^{2}\), using Young’s inequality, we get
where we used (3.42), (3.43) and (3.38) in the last term, \(C(f_{\mathrm {in}})\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{2}}\) and \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\). Since
we get that
for some positive constant \(C_{0}\) depending only on \(\Vert f_{\mathrm {in}}\Vert _{L^{1}_{2}}\), \(\Vert f_{\mathrm{in}}\Vert _{L^{2}}\) and \(H(f_{\mathrm{in}})\).
Choosing \(q >1\), \(a >0\) and \(\theta \in (0,1)\) such that \(q'\,\theta =1\) and
and applying Hölder’s inequality, we see that, with \(\varpi =\max (-\gamma ,2+\gamma )\),
Using the Sobolev inequality (2.14), we conclude that
At this point, observe that \(\theta = \frac{2p}{3p-1}\) and select a in such a way that \(aq = 3|\gamma |\). Thus,
with \(\varvec{z}_{p}=\frac{\varpi +a}{\theta }\). Note that, for \(\gamma \in (-2,0)\), \(\varvec{z}_{p} \leqslant \frac{6p-4}{p} < 6\). Then, using Young’s inequality it holds for any \(\delta >0\),
Choosing \(C_{0}\,C_{p}\,\delta ^{\frac{1}{3}} = \frac{1}{2p^{2}} \, K_0\), we get after combining (A.4) and (A.5) that
One sees from the second part of (1.14) in Theorem 1.9 that
for some \(C_{p}(f_{\mathrm{in}})\) depending only on \(\Vert f_{\mathrm{in}}\Vert _{L^{1}_{2}}\), and \(H(f_{\mathrm{in}})\) and p. We deduce from this estimate (A.2). \(\square \)
For simplicity of notations, we introduce here \(L^{1}_{\infty }({\mathbb {R}}^{3}) :=\bigcap _{s\geqslant 0}L^{1}_{s}({\mathbb {R}}^{3})\) as the space of integrable functions with finite moments of any order and, more generally,
for any \(p\geqslant 1\).
Corollary A.2
Assume \(-2<\gamma <0\) and let \(q_0 >1\). We assume that \(f_{\mathrm {in}}\in L^{q_0}({\mathbb {R}}^3) \cap L^{2}({\mathbb {R}}^{3})\cap L^1_{\infty }({\mathbb {R}}^{3})\) satisfies (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and f(t, v) be a weak solution to (1.11.10). Then, for any \(m >0, q \in [1,q_{0})\) and for any \(T>0\), there exists some constant C depending on \(q_0\), m, q, \(f_{\mathrm{in}}\) such that
Proof
This is a direct consequence of an interpolation between the spaces \(L^{q_0}\) and \(L^1_{s}\), using Proposition A.1 and the universal growth of the \(L^{1}\)-moments in Theorem 1.9. \(\square \)
This corollary will be used in a crucial way to prove the following proposition. We introduce here the notation \(L^{\infty -0}({\mathbb {R}}^{3}) :=\bigcap _{q \geqslant 1}L^{q}({\mathbb {R}}^{3})\).
Proposition A.3
Assume \(-2<\gamma <0\) and let \(f_{\mathrm {in}}\in L^1_{\infty }({\mathbb {R}}^{3}) \bigcap L^{\infty -0}({\mathbb {R}}^3)\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and f(t, v) be a weak solution to (1.11.10). For any choice of \(m \geqslant 0\) and \(p \geqslant 2\), if \(f_{\mathrm{in}} \in W^{1,p}_{m}({\mathbb {R}}^{3})\), then there is some \(C_T(f_{\mathrm {in}})\) depending on m, p, T and \(f_{\mathrm {in}}\) such that
Proof
Taking the derivative of (1.11.10) with respect to a component \(i \in \{1,2,3\}\), we end up with the equation
Compute
Using the coercivity estimate in Proposition 2.3 and Young’s inequality we see that
where \(C_p>0\) only depends on p and m. Then, we observe that
and (A.9) leads to
For \(p >2\), using Young’s inequality \(x\,y \leqslant x^a + y^{\frac{a}{a-1}}\) with \(a=\frac{p}{p-2}\) for the second term of the right-hand side of the aforementioned estimate, and with \(a =\frac{p}{p-1}\) for the third term, we conclude that for some \(r_1, r_2 \geqslant 0\)
Such an inequality is also easily deduced from (A.12) when \(p=2\). We see then, thanks to Young’s inequality, that for all \(r_3\geqslant 0\), there exists \(r_4\geqslant 0\) such that
where we used that
and \(\int _{{\mathbb {R}}^{3}}\langle v\rangle ^{-4}\,\mathrm {d}v < \infty \). Then,
The second integral is nonnegative whereas we can estimate the third integral using Young’s inequality to get, for any \(\delta >0\),
To estimate the first integral, we now use Young’s inequality in the form
while, for the third integral, since \(\max (3|\gamma |,4-|\gamma |) {\leqslant } \max (|\gamma |,2-|\gamma |)+2\max (|\gamma |,1)\), one can use Young’s inequality in the form
for some positive constant \(C_{\delta ,p} >0\). Therefore, one can find \(C_{\delta ,p}>0\) such that
with \(r_{5}:=m + \max (|\gamma |, 2 - |\gamma |)-p\), \(r_{6}:=m + \max (|\gamma |, 2 - |\gamma |) + p\,\max (|\gamma |,1).\) As a consequence,
Using estimates (A.14), (A.15), (A.13), and remembering (A.6), we conclude the proof. \(\square \)
Notice that in particular, thanks to Proposition A.3, a Sobolev estimate in the v variable shows that f satisfies an \(L^{\infty }\) (local w.r.t. time) estimate. More specifically, we have the following result
Corollary A.4
Assume \(-2<\gamma <0\), and let \(f_{\mathrm {in}}\in L^{\infty -0}({\mathbb {R}}^3) \cap L^1_{\infty }({\mathbb {R}}^{3}) \) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and let f(t, v) be a weak solution to (1.11.10). Then for any \(p > 2\) and any \(T >0\), if \(f_{\mathrm {in}}\in W^{1,p}_{2}({\mathbb {R}}^3)\), there is some \(C_T(p, f_{\mathrm {in}})\) depending on p, T and \(f_{\mathrm {in}}\), such that
Proof
Observe that thanks to (A.10) and (A.11),
so that \(\langle \cdot \rangle ^{-2-\gamma }\varvec{\Sigma }[f]\) is bounded in \(L^{\infty }([0,T]\times {\mathbb {R}}^{3})\). In the same way \(\langle \cdot \rangle ^{\min \{-1-\gamma ,0\}}\varvec{b}[f]\) is bounded in \(L^{\infty }([0,T] \times {\mathbb {R}}^3)\). We conclude using Proposition A.3 and Corollary A.2. \(\square \)
Corollary A.5
Assume \(-2<\gamma <0\) and let \(f_{\mathrm {in}}\in L^{\infty -0}({\mathbb {R}}^3) \cap L^1_{\infty }({\mathbb {R}}^{3})\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and let f(t, v) be a weak solution to (1.11.10). Then for any \(p > 2\), \(T>0\), if \(f_{\mathrm {in}}\in W^{1,p}_{2}({\mathbb {R}}^3)\) then there is some \(C_T(p, f_{\mathrm {in}})\) depending on T, p and \(f_{\mathrm {in}}\), such that
and for any \(\alpha \in (0, \frac{1}{3}), T >0\), there is some \(C_T(\alpha , f_{\mathrm {in}})\) depending on T, \(\alpha \) and \(f_{\mathrm {in}}\), such that
Proof
Using the equation and Corollary A.4, we see that, for all \(1 \leqslant p < \infty \), if \(f_{\mathrm {in}}\in W^{1,p}_{2}({\mathbb {R}}^3)\) then f is bounded in \(W^{1,\infty }((0,T) ; W^{-1, p}({\mathbb {R}}^3))\). Proposition A.3 also ensures that f is bounded in \( L^{\infty }((0,T); W^{1, p}({\mathbb {R}}^3))\). We get inequality (A.17) thanks to an interpolation, and deduce (A.18) from (A.17) thanks to a Sobolev inequality. \(\square \)
We now establish a weighted \(L^{\infty }\) estimate which comes out of Prop. A.3.
Corollary A.6
Assume \(-2<\gamma <0\) and let \(f_{\mathrm {in}}\in L^{1}_{\infty }({\mathbb {R}}^3) {\cap L^{\infty -0}({\mathbb {R}}^3)}\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and f(t, v) be a weak solution to (1.11.10). For any choice of \(m \geqslant 0\) and \(p > 3\), if \(f_{\mathrm {in}}\in W^{1,p}_m({\mathbb {R}}^3)\), then there is some \(C_T(m,p,f_{\mathrm {in}})\) depending on m, p, T and \(f_{\mathrm {in}}\) such that
Proof
Notice that, if \(f_{\mathrm{in}} \in W^{1,p}({\mathbb {R}}^{3})\) with \(p >3\), then \(f_{\mathrm{in}} \in L^{\infty }\) thanks to Sobolev inequality. In particular, the assumptions of Propositions A.3 and Corollary A.2 are met. Using Sobolev inequality again, since \(p >3\), there are \(C_{0}=C_{0}(m,p),\) \(C_{1}=C_{1}(m,p)\) such that
We conclude by using Proposition A.3 and Corollary A.2. \(\square \)
We can now state a stability estimate for the solutions of the LFD equation satisfying the regularity obtained in Proposition A.3.
Proposition A.7
Assume \(-2<\gamma <0\) and let \(f_{\mathrm {in}}, g_{\mathrm {in}}\in L^{1}_{\infty }({\mathbb {R}}^3) {\cap L^{\infty -0}({\mathbb {R}}^3)} \) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and f(t, v), g(t, v) be weak solutions to (1.11.10). If \(f_{\mathrm {in}}, g_{\mathrm {in}}\in W^{1,4}_{\infty }({\mathbb {R}}^3),\) then for all \(m \geqslant 8\), there is some \(C_T(m, f_{\mathrm {in}} , g_{\mathrm {in}})\) depending on m, T and \(f_{\mathrm {in}}, g_{\mathrm {in}}\) such that
Proof
In the rest of the proof, C will denote a positive constant depending on \(m,T, {f_{\mathrm {in}}, g_{\mathrm {in}}}\) as well as the coercivity constant \(K_{0}\) and that may change from one line to another. For two solutions f(t, v), g(t, v) to (1.11.10), we introduce
from which one sees easily that
Using the short-hand notations \({\mathsf {h}}=f(1-\varvec{\varepsilon }f)+g(1-\varvec{\varepsilon }g),\) \(\varvec{\Sigma }_{0}=\varvec{\Sigma }[f]+\varvec{\Sigma }[g]=\varvec{\sigma }[{\mathsf {h}}]\), we compute, for \(m \geqslant 0\),
Here, arguing exactly as in [12, Proof of Theorem 5.2, estimate of (5.2) + (5.4)], we can check that
Observing that there is \(C >0\) such that \( \left| \varvec{\Sigma }_{0}\,:\nabla ^{2}\langle v\rangle ^{m}\right| \leqslant C\langle v\rangle ^{m+\gamma },\) while
thanks to (3.44), we can estimate the integrals involving \( \int _{{\mathbb {R}}^{3}}{\mathsf {u}}^{2}\langle v\rangle ^{m} \varvec{c}[{\mathsf {s}}] \,\mathrm {d}v\) and \( \int _{{\mathbb {R}}^{3}}{\mathsf {u}}^{2}\langle v\rangle ^{m}\varvec{c}[\mathsf {s+h}] \,\mathrm {d}v\) using Proposition 1.8 and deduce that
By Young’s inequality, the last term can be bounded by
for some positive constant \(C_{0}\) depending on \(K_{0}\). Using the bound in (A.19) together with the bound on \(|\varvec{b}[s]|\) provided by (A.11), one checks without difficulty that there exists \(C >0\) such that
and therefore
i.e.
where we used again (A.21). We now estimate \(I_{3}\) and \(I_{4}\). Since
and, thanks to Young’s inequality,
while
Therefore,
One has \(|{\mathsf {h}}|^{2} \leqslant {\mathsf {s}}^{2}\) and, using again (A.19), there is \(C >0\) such that \(\langle v\rangle ^{m-\gamma +6}{\mathsf {h}}^{2}\leqslant C\), from which
Splitting the convolution integral according to \(|v-v_{*}| \geqslant 1\) and \(|v-v_{*}| <1\), we see that
and, using Cauchy-Schwarz inequality, we see that
from which
Using now the estimate of \(\nabla {\mathsf {s}}\) as deduced from Prop. A.3 in the form
we can apply twice Cauchy-Schwarz inequality to deduce that
from which
Combining this with (A.23) we see that
Combining this with the estimate (A.22) of \(I_{1}+I_{2}\) we deduce that
Taking \(m \geqslant 8\) and using Gronwall’s lemma, we get the stability estimate (A.7A.16A.20). \(\square \)
We conclude this Appendix with the proof that (for suitable initial data) the solutions of the LFD equation with moderately soft potentials are in fact classical.
Corollary A.8
Let \(\gamma \in (-2,0)\). Consider an initial datum \(f_{\mathrm {in}}\in L^{\infty -0}({\mathbb {R}}^3) \cap L^1_{\infty }({\mathbb {R}}^{3})\cap W^{1,p}_2({\mathbb {R}}^3)\) for some \(p>2\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0 >0\). For any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_{0}]\), any weak solution f to (1.11.10) given by Theorem 1.5 is actually a classical solution, that is f is continuously differentiable with respect to t and twice continuously differentiable with respect to v on \((0, \infty )\times {\mathbb {R}}^3\).
Proof
We observe that f is a weak solution to the linear equation (with unknown u)
Let \(R>0\) and \(\Omega =\{v\in {\mathbb {R}}^3 ; |v|\leqslant R\}\). The coefficients \(\varvec{\Sigma }[f]\), \((1-2\varvec{\varepsilon }\,f)\varvec{b}[f]\), \(\varvec{c}_\gamma [f]\,(1-\varvec{\varepsilon }\,f) \) and also \(\nabla \varvec{\Sigma }[f]\) are Hölder-continuous on \((0,T) \times \Omega \) for any \(T >0\) thanks to Corollary A.5 and belong to \(L^\infty ((0,T) \times \Omega )\). We then deduce from Proposition 2.3 and [30, Chapter III, Theorem 12.1] that \(\partial _tf\) and \(\partial ^2_{v_i v_j} f\) are also Hölder-continuous on \((0,\infty ) \times \Omega \). \(\square \)
We now have all the ingredients for the
Proof of Theorem 1.6
The first statement in the Theorem is a direct consequence of Corollary A.2, while the second one is obtained thanks to Proposition A.3 and Corollary A.5 whenever \(p > 2\). For \(p \in [1,2]\), one deduces that \(f \in L^{\infty }([0,T]; W^{1,p}_s({\mathbb {R}}^3))\) by a simple interpolation. The uniqueness part of the result is deduced from the stability estimate (A.7A.16A.20) in Proposition A.7. \(\square \)
Appendix B. About the Cauchy Theory
We give the detailed proof of Theorem 1.5 about the existence of solutions to (1.11.10). We follow the approach of [12]. Let \((\Psi _\nu )_{\nu \in (0,1)}\) be a family of smooth bounded functions on \({\mathbb {R}}_+\) that coincide with \(\Psi (r)=r^{\gamma +2}\) for \(0<\nu<r<\nu ^{-1} \) and satisfy that
-
(i)
The functions \(\Psi _\nu '\), \(\Psi _\nu ''\), \(\Psi _\nu ^{(3)}\) and \(\Psi _\nu ^{(4)}\) are bounded.
-
(ii)
The following hold
$$\begin{aligned} \Psi _\nu (r)\geqslant \frac{\nu ^\gamma r^{2}}{2}\; \qquad \forall \, 0< r <\nu \,, \quad \Psi _\nu (r) \geqslant \frac{\nu ^{-(2+\gamma )}}{2}>0, \forall \, r >\nu ^{-1}\,. \end{aligned}$$(B.1) -
(iii)
For any \(r\in {\mathbb {R}}_+\),
$$\begin{aligned} \Psi _\nu (r)\leqslant 2 \,r^{2+\gamma } \qquad \text { and } \qquad |\Psi '_\nu (r)|\leqslant C r^{1+\gamma }, \end{aligned}$$(B.2)for some constant C independent of \(\nu \).
We then set
and we consider the following regularized problem
where, as above, \(\varvec{\Sigma }^{\nu }[f]= a^{\nu }*(f(1-\varvec{\varepsilon }f))\), \(\varvec{b}^{\nu }[f]=b^{\nu }*f\).
We note here that the initial condition of the regularized problem is not assumed to satisfy (1.9). For such an initial condition, Lemma 2.1 still holds. We first investigate the well-posedness of (B.3) and prove the following result.
Proposition B.1
Consider \(f_{\mathrm {in}} \in {\mathscr {C}}^\infty ({\mathbb {R}}^3)\cap H^1({\mathbb {R}}^3) \cap W^{3,\infty }({\mathbb {R}}^3)\) such that
for some positive constants \(\alpha _1\), \(\alpha _2\), \( \beta _1\) and \(\beta _2\). Let \(\nu >0\) and \(T>0\). Then, there exists a solution \(f^\nu \) to the regularized problem (B.3) such that, for every \(s>0\),
The proof of this Proposition can be easily adapted from the proof of [12, Theorem 4.2]. One begins by freezing the non-local coefficients in (B.3). The smoothness and boundedness of \(\Psi _\nu \) are used here in order to obtain some parabolic operator with smooth coefficients and deduce the existence of a unique classical solution from [30, Chapter V, Theorem 8.1]. Finally, some fixed-point argument enables to conclude.
In order to pass to the limit \(\nu \rightarrow 0\) in (B.3) and obtain a solution to (1.11.10), we need to prove uniform estimates on \(f^\nu \) (with respect to \(\nu \)). First, as in [12, Lemma 4.8], one has the lemma:
Lemma B.2
For any \(\sigma , t\in [0,T]\), \(\sigma \leqslant t\), for any \(\nu \in (0,1)\), the function \(f^\nu \) satisfies
where \(\varrho = \displaystyle \int _{{\mathbb {R}}^3} f_{\mathrm {in}}(v)\,\mathrm {d}v\) and \(\theta =\displaystyle \int _{{\mathbb {R}}^3} f_{\mathrm {in}}(v) \,|v|^2\,\mathrm {d}v\).
Next, we consider the ellipticity of the diffusion matrix. As in [12, Proposition 4.9 and Corollary 4.10], one has the following proposition:
Proposition B.3
Let \(0\leqslant f_{\mathrm {in}}\in L^{1}_{2}({\mathbb {R}}^{3})\) be fixed and satisfying (1.7) for some \(\varvec{\varepsilon }_0 >0\). Let \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and \(R(f_{\mathrm {in}})\) and \(\eta (f_{\mathrm {in}})\) be given by the first point of Lemma 2.1. Let \({\overline{\eta }}\) be the constant given by the second point of Lemma 2.1 for \(\delta =\eta (f_{\mathrm {in}})\). Let
Then,
-
(1)
there exists a positive constant \(K_{0} > 0\) depending on \(\gamma \), \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\), and \(H(f_{\mathrm {in}})\), such that, for any \(v,\, \xi \in {\mathbb {R}}^3\),
$$\begin{aligned}&\sum _{i,j} \, \left( \varvec{\Sigma }_{i,j}[f](v) +\nu \, \delta _{i,j} \right) \, \xi _i \, \xi _j \\&\quad \geqslant K_{0} \langle v \rangle ^{\gamma } \,\min \left\{ (\nu ^{-1}|v|)^{-\gamma }, 2^{-\gamma }, 2(\nu |v|)^{-(2+\gamma )}\right\} |\xi |^2 \end{aligned}$$holds for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\);
-
(2)
there exists a positive constant \(\kappa > 0\) depending on \(\gamma \), \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\), and \(H(f_{\mathrm {in}})\), such that
$$\begin{aligned} \forall \, v,\, \xi \in {\mathbb {R}}^3, \qquad \sum _{i,j} \, \left( \varvec{\Sigma }_{i,j}[f](v) +\nu \, \delta _{i,j} \right) \, \xi _i \, \xi _j \geqslant \kappa \; \frac{ |\xi |^2}{1+|v|^2}, \end{aligned}$$holds for any \(\varvec{\varepsilon }\in (0,\varvec{\varepsilon }_0]\) and \(f \in {\mathcal {Y}}_{\varvec{\varepsilon }}(f_{\mathrm {in}})\).
The proof of the first point of this Proposition can be easily adapted from that of [24, Proposition 2.3]. Indeed, \(\Psi _\nu \)may be bounded from below thanks to (B.1):
The second point follows easily from the proof of the first point by using that \(\nu ^{-1} \geqslant 3R(f_{\mathrm {in}})\). This gives some uniform (with respect to \(\nu \)) ellipticity estimate.
Lemma B.4
Let \(f_{\mathrm {in}}\in {\mathscr {C}}^\infty ({\mathbb {R}}^3)\cap H^1({\mathbb {R}}^3) \cap W^{3,\infty }({\mathbb {R}}^3)\) satisfying (B.4). Let \(f^\nu \) be a solution to (B.3) given by Proposition B.1. Then, for any \(T>0\) and \(s>2\), there exists some constant \(C_s\) depending only on s, T and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\) such that
Proof
With notations similar to those in (3.1), one has
where
As in Lemma 3.1 and Remark 3.2 one has
One now splits \({\mathscr {J}}^\nu _{s,2}(f^\nu ,F^\nu )\) according to \(|v-v_{*}|\geqslant 1\) and \(|v-v_{*}|< 1\) ,
where
Since \(|v|^2 |v_{*}|^2 -(v\cdot v_{*})^2 \leqslant \langle v \rangle ^2 \langle v_{*}\rangle ^2\), \(\Psi _\nu \) satisfies (B.2) and \(F^\nu \leqslant f^\nu \), one has
where \(\varvec{m}_{s}^{\nu }(t) = \int _{{\mathbb {R}}^3} f^{\nu }(t,v) \langle v \rangle ^s \,\mathrm {d}v\). For \(I_2\), we use (B.2), \(F^\nu \leqslant f^\nu \), and \(|v|^2|v_{*}|^2 -(v\cdot v_{*})^2 \leqslant |v|\, |v_{*}|\, |v-v_{*}|^2\,,\) to get that
One also splits \({\mathscr {J}}^\nu _{s,1}(f^\nu ,(f^\nu )^2)\) according to \(|v-v_{*}|\geqslant 1\) and \(|v-v_{*}|< 1\),
where
Since \(\Psi _\nu \) satisfies (B.2) and \(\varvec{\varepsilon }f^\nu \leqslant 1\), one has
For \(J_2\), we use that \(\Psi _\nu (r)\leqslant 2\) for \(r<1\) by (B.2) and \(\varvec{\varepsilon }f^\nu \leqslant 1\). We also have \(|v_{*}\cdot (v_{*}-v)|\leqslant |v_{*}| \, |v-v_{*}| , \) and
Hence,
for some C depending only on s. Consequently, if \(s\leqslant 3\), we obtain
whereas, if \(s>3\),
Finally,
Combining the above estimates and (B.5)-(B.6), we deduce the existence of some constant \(C_s\) depending on s, \(\gamma \), T and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\) such that \(\frac{\mathrm {d}}{\mathrm {d}t }\varvec{m}^\nu _s(t) \leqslant C_s \varvec{m}^\nu _s(t), \) and (B.8) follows. \(\square \)
Lemma B.5
Let \(f_{\mathrm {in}}\in {\mathscr {C}}^\infty ({\mathbb {R}}^3)\cap H^1({\mathbb {R}}^3) \cap W^{3,\infty }({\mathbb {R}}^3)\) satisfying (B.4). Let \(f^\nu \) be a solution to (B.3) given by Proposition B.1. Then, for any \(T>0\) and \(s\geqslant 2\), there exists some constant \(C>0\) depending only on s, \(\varvec{\varepsilon }\), T and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\) such that, for any \(t\in (0,T)\),

with

Proof
Let \(s\geqslant 0\). We deduce from (B.3) that
It follows from the second point of Proposition B.3 that
Proceeding as in the proof of (3.12), we obtain

where \(\varvec{A}(v)=\langle v\rangle ^{2}\mathbf {Id}+(s-2)\,v\otimes v\), \(v \in {\mathbb {R}}^{3}.\) For the last two integrals in (B.11), we clearly have

and

For the integral involving \(\varvec{A}\) in (B.11), we have by (B.2), for every i, j, \(|\varvec{A}_{i,j}|\leqslant s\langle v\rangle ^2\) and \(| \varvec{\Sigma }^\nu _{i,j}[f^\nu ]| \leqslant 2\Psi ^\nu *f^\nu \leqslant 4 |\cdot |^{2+\gamma } *f^\nu \,. \) Hence,

For the first integral in (B.11), since \(0\leqslant \frac{1}{3} (f^\nu )^2\leqslant (f^\nu )^2- \frac{2\varvec{\varepsilon }}{3} (f^\nu )^3 \leqslant (f^\nu )^2\), we have, by (B.2),
Now, as for (3.42)-(3.43), there exists some universal constant \(C>0\) such that for every \(v\in {\mathbb {R}}^3\) and every \(t\in [0,T]\),
where we used that \(f^\nu \leqslant \varvec{\varepsilon }^{-1}\). Consequently, we get that

Similarly, since \(\varvec{\varepsilon }(f^\nu )^2 \leqslant f^\nu \), one has

For the second integral in (B.11), since \(0\leqslant \frac{1}{6} (f^\nu )^2 \leqslant \frac{1}{2} (f^\nu )^2-\frac{\varvec{\varepsilon }}{3} (f^\nu )^3 \leqslant \frac{1}{2} (f^\nu )^2\), we have by (B.2)
Now, for a given \(v\in {\mathbb {R}}^3\), one has, thanks to the Hölder inequality,
for \(p>1\) such that \(-\gamma q<3\) where \(\frac{1}{p}+\frac{1}{q}=1\). Hence,

For \(\nu \in (0,1)\) and \(\gamma \in (-2,0)\), Lemma B.2 implies that all the above \(L^1\)-moments are bounded by some constant depending only on T and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\). Thus, gathering the above estimates, (B.9) follows.\(\square \)
Remark B.6
Performing the same manipulations as above but using the first point of Proposition B.3, one obtains

where again C depends on s, \(\varvec{\varepsilon }\), T and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\).
Proof of Theorem 1.5
Let us fix \(T>0\). Consider \(f_{\mathrm {in}}\in L^1_{s_0}({\mathbb {R}}^3)\) for some \(s_0>2\) satisfying (1.7)–(1.9) for some \(\varvec{\varepsilon }_0>0\). Then, there exists a sequence of functions \(( f_{\mathrm {in},k})_{k\geqslant 1}\) in \({\mathscr {C}}^\infty ({\mathbb {R}}^3)\cap H^1({\mathbb {R}}^3) \cap W^{3,\infty }({\mathbb {R}}^3)\) such that \(( f_{\mathrm {in},k})_{k\geqslant 1}\) converges towards f in \(L^1_{s_0}({\mathbb {R}}^3)\) and
for some positive constants \(\alpha _k\), \(\alpha '_k\), \(\beta _k\) and \(\beta '_k\).
For every \(k\in {\mathbb {N}}_*\), we set \(\nu _k=\frac{1}{k}\) and \(f_k=f^{\nu _k}\), where \(f^{\nu _k}\) denotes a solution to (B.3) with initial datum \( f_{\mathrm {in},k}\) given by Proposition B.1. Since \((f_{\mathrm {in},k})_{k\geqslant 1}\) is bounded in \(L^1_{s_0}({\mathbb {R}}^3)\), we deduce from Lemma B.4 that \((f_k)_{k\geqslant 1}\) is bounded in \(L^2((0,T);L^1_{s_0}({\mathbb {R}}^3))\). We now apply Lemma B.5 with \(s=s_0> 2\). Since \((f_{\mathrm {in},k})_{k\geqslant 1}\) is bounded in \(L^1_{s_0}({\mathbb {R}}^3)\cap L^\infty ({\mathbb {R}}^3)\), it is bounded in \( L^2_{s_0}({\mathbb {R}}^3)\) and we deduce that there exists some constant \(C_{T,\varvec{\varepsilon }}\) depending on T, \(\varvec{\varepsilon }\) and \(\sup _{k\geqslant 1}\Vert f_{\mathrm {in},k}\Vert _{L^1_{s_0}}\) such that, for any \(k\in {\mathbb {N}}_*\),
Consequently, \((f_k)_{k\geqslant 1}\) is bounded in \(L^2((0,T);H^1({\mathbb {R}}^3))\). We then deduce from the weak formulation associated to (B.3) that \((\partial _tf_k)_{k\geqslant 1}\) is bounded in \(L^1((0,T);(W^{2,\infty }({\mathbb {R}}^3))')\) and thus, for \(m\geqslant 4\), in \(L^1((0,T);(H^m({\mathbb {R}}^3))')\). Now, for \(m\geqslant 4\), we have
the embedding of \(H^1({\mathbb {R}}^3)\cap L^1_{s_0}({\mathbb {R}}^3) \) in \(L^1({\mathbb {R}}^3)\) being compact. We may thus conclude from [31, Corollary 4] that \((f_k)_{k\geqslant 1}\) is relatively compact in the space \(L^2((0,T);L^1({\mathbb {R}}^3))\). Therefore, there exists a function \(f\in L^2((0,T);L^1({\mathbb {R}}^3))\) and a subsequence of \((f_k)_{k\geqslant 1}\) (not relabelled) such that \((f_k)_{k\geqslant 1}\) converges towards \(f\in L^2((0,T);L^1({\mathbb {R}}^3))\) and a.e. on \((0,T)\times {\mathbb {R}}^3\). For \(\varphi \in {\mathscr {C}}_0^2({\mathbb {R}}^3)\), it is easy to check that the sequence \((\int _{{\mathbb {R}}^3} f_k \varphi \, \,\mathrm {d}v)_{k\geqslant 1}\) is equicontinuous and bounded in \({\mathscr {C}}([0,T])\). The Arzelà-Ascoli Theorem thus ensures that it is relatively compact in \({\mathscr {C}}([0,T])\).
Finally, we obtain that \((\int _{{\mathbb {R}}^3} f_k \varphi \, \,\mathrm {d}v)_{k\geqslant 1}\) converges towards \(\int _{{\mathbb {R}}^3} f \varphi \, \,\mathrm {d}v\) in \({\mathscr {C}}([0,T])\) and then that \((f_k)_{k\geqslant 1}\) converges towards f in \({\mathscr {C}}_w([0,T];L^2({\mathbb {R}}^3))\), where \({\mathscr {C}}_w([0,T];L^2({\mathbb {R}}^3))\) denotes the space of weakly continuous functions in \(L^2({\mathbb {R}}^3)\). We easily check that f preserves mass and energy and, passing to the limit \(k\rightarrow \infty \) in the weak formulation, we obtain that f satisfies (1.11). Moreover, we can deduce from (B.8) that \(f\in L^\infty ((0,T);L^1_{s_0}({\mathbb {R}}^3))\), and from Remark B.6 that \(\nabla f \in L^{2}((0,T);L^{2}_{s_0+\gamma }({\mathbb {R}}^{3})).\)
Let us now prove the monotonicity of the entropy. We know that \(f\in L^2((0,T); H^1_{2+\gamma }({\mathbb {R}}^3))\). Then, we deduce as in (B.12) that there exists some constant \(C_{\varvec{\varepsilon }}\) depending on \(\varvec{\varepsilon }\) and \(\Vert f_{\mathrm {in}}\Vert _{L^1_2}\) such that, for every \(v\in {\mathbb {R}}^3\) and \(t\in [0,T]\)
One also has, for every \(v\in {\mathbb {R}}^3\) and every \(t\in [0,T]\), that \(|\varvec{\Sigma }[f](t,v)| \leqslant C\Vert f_{\mathrm {in}}\Vert _{L^1_2} \,\langle v \rangle ^{2+\gamma },\) for some universal constant \(C>0\). It thus follows from the weak formulation associated to (1.11.10) that \(\partial _t f\in L^2((0,T);(H^1_{2+\gamma }({\mathbb {R}}^3))')\). We then deduce from [32, Ch.III Lemma 1.2] that \(f\in {\mathscr {C}}([0,T];L^2({\mathbb {R}}^3))\). As in [12, Lemma 4.18], one may then prove the monotonicity of \({\mathcal {S}}_{\varvec{\varepsilon }}(f)\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alonso, R., Bagland, V., Desvillettes, L. et al. About the Landau-Fermi-Dirac Equation With Moderately Soft Potentials. Arch Rational Mech Anal 244, 779–875 (2022). https://doi.org/10.1007/s00205-022-01779-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-022-01779-z



 , then since
, then since  for any
for any  and
and  for any
for any 
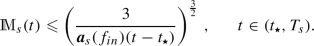
 and
and  for some
for some 

 by continuity, we deduce that
by continuity, we deduce that  for all
for all 

 for any
for any