The reference frames of Mercury after the MESSENGER mission

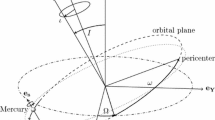
Abstract

We report on recent refinements and the current status for the rotational state models and the reference frames of the planet Mercury. We summarize the performed measurements of Mercury rotation based on terrestrial radar observations as well as data from the Mariner 10 and the MESSENGER missions. Further, we describe the different available definitions of reference systems for Mercury and obtain the corresponding reference frame using data provided by instruments on board MESSENGER. In particular, we discuss the dynamical frame, the principal-axes frame, the ellipsoid frame, as well as the cartographic frame. We also describe the reference frame adopted by the MESSENGER science team for the release of their cartographic products, and we provide expressions for transformations from this frame to the other reference frames.

Appendices

Appendix A: extended dynamical frame

Recently, Baland et al. (2017) have extended the Cassini state model to account for pericenter precession and tidal deformation of Mercury. Thereby, the authors express the orientation of Mercury with respect to its Laplace plane. For the transformation to the ICRF from the reference frame defined by the Laplace plane normal and the node of Laplace plane and ICRF equator [also used by Baland et al. (2017)] we use the following transformation matrix

$$\begin{aligned} \left( {{\begin{array}{ccc} {0.06140463088547411}&{} {0.9978489634266365}&{} {0.02295468349172782} \\ {-\,0.9346751836048649}&{} {0.06555490971991894}&{} {-\,0.3494064323460937} \\ {-\,0.35015963853509846}&{} 0&{} {0.9366900381347978} \\ \end{array} }} \right) , \end{aligned}$$

Table 4 MDIS NAC and WAC images used for measurement of the diameter and crater center coordinates of Hun Kal. Weighted averages are obtained by weighting the measurements by the ratio of viewing quality scale and image resolution

which is based on the orbital elements of Stark et al. (2015). In particular, the ICRF spherical coordinates of the Laplace pole are given by $\left( {69.5029204^{\circ },\, 273.7587151^{\circ }} \right)$.

We express the rotational angles as functions of the precession amplitude $\varepsilon _{\Omega }^{k_2 }$, nutation amplitude $\varepsilon _{\omega }^{k_2 }$ and the tidal deviation amplitude $\varepsilon _\zeta$ (see Eqs. 64 to 66 of Baland et al. (2017)). These amplitudes are connected to the interior structure of Mercury, in particular to the normalized polar moment of inertia C/MR$^{2}$, the tidal Love number $k_2$ and the tidal quality factor Q. The Cassini state declination $\delta ^{\mathrm{eCS}}$, right ascension $\alpha ^{\mathrm{eCS}}$ and prime meridian angle $W^{\mathrm{eCS}}$ with respect to the International Celestial Reference Frame (ICRF) are

$$\begin{aligned} \delta ^{\mathrm{eCS}}( t )= & {} 61.44780272^{\circ }-0.95540886^{\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ } \nonumber \\&+\,0.46675751^{\circ }\varepsilon _{\omega }^{k_2 } /^{\circ }+0.2952861^{\circ }\varepsilon _\zeta /^{\circ } \nonumber \\&+\,( -0.00484640^{\circ }-0.00041197^{\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ } \nonumber \\&+\,0.00694873^{\circ }\varepsilon _{\omega }^{k_2 } /^{\circ }-0.00133294^{\circ }\varepsilon _\zeta /^{\circ })t/\hbox {cy} \nonumber \\&+\,0.00001960^{\circ }( {t/\hbox {cy}} )^{2} \end{aligned}$$

(4)

$$\begin{aligned} \alpha ^{\mathrm{eCS}}(t )= & {} 280.98797069^{\circ }+0.61780624^{\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ }\nonumber \\&+\,1.84941502^{\circ }\varepsilon _{\omega }^{k_2 } /^{\circ }+1.99893401^{\circ }\varepsilon _\zeta /^{\circ }\nonumber \\&+\,(-\,0.03280760^{\circ }-0.00288486^{\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ }\nonumber \\&-\,0.00805508^{\circ }\varepsilon _{\omega }^{k_2 } /^{\circ } +0.00055120^{\circ }\varepsilon _\zeta /^{\circ })t/\hbox {cy} \nonumber \\&-\,0.00002449^{\circ }(t/\hbox {cy})^{2} \end{aligned}$$

(5)

$$\begin{aligned} W^{\mathrm{eCS}}\left( t \right)= & {} 329.75640656^{\circ }-0.54266991^{\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ }\nonumber \\&-1.62449296^{\circ }\varepsilon _{\omega }^{k_2 } /^{\circ }-1.7558277^{\circ }\varepsilon _\zeta /^{\circ } \nonumber \\&+(6.138506839^{\circ }+7.01\times 10^{-8\circ }\varepsilon _{\Omega }^{k_2 } /^{\circ }\nonumber \\&+19.58\times 10^{-8\circ }\varepsilon _{\omega }^{k_2 } /^{\circ }\nonumber \\&-1.10\times 10^{-8\circ }\varepsilon _\zeta /^{\circ })t/\hbox {d} +W_{\mathrm{lib}} \left( t \right) \end{aligned}$$

(6)

Thereby, t is the time and is measured in centuries (cy) (in case of $\delta ^{\mathrm{eCS}}$ and $\alpha ^{\mathrm{eCS}})$ and in days (d) (for $W^{\mathrm{eCS}})$. The three obliquity parameters $\varepsilon _{\Omega }^{k_2 }$, $\varepsilon _{\omega }^{k_2 }$ and $\varepsilon _\zeta$ are measured in degrees, and the term $W_{\mathrm{lib}} \left( t \right)$ denotes the longitudinal libration terms. For the case of a rigid Mercury ($k_2 \rightarrow 0)$ and neglecting the effect of the pericenter precession ($\varepsilon _{\omega }^{k_2 } \rightarrow 0$ and $\varepsilon _\zeta \rightarrow 0)$ the obliquity parameter $\varepsilon _{\Omega }^{k_2 }$ becomes the Cassini state obliquity $\varepsilon _{\Omega }$ and coincides with Eqs. 1–3 in Sect. 2.1.

With the help of the provided equations and given an observation of Mercury’s rotation axis orientation at a specific epoch t’ and an independent measurement of the tidal Love number $k_{2 }$ it is possible to solve for the normalized polar moment of inertia C/MR$^{2}$ and the tidal quality factor Q. Furthermore, once the parameters $\varepsilon _{\Omega }^{k_2 }$, $\varepsilon _{\omega }^{k_2 }$ and $\varepsilon _\zeta$ are determined it is straightforward to derive the orientation and precession rate of the rotation axis at the J2000.0 epoch (Baland et al. 2017). Using the observations for the rotation axis orientation of Stark et al. (2015) at MJD56353.5 TDB and $k_2 =0.5\pm 0.1$ Baland et al. (2017) have obtained $C/MR^{2}=0.3433\, \pm \, 0.0134$ and $Q=89\pm 261.$ The corresponding amplitudes are $\varepsilon _{\Omega }^{k_2 } =2.032\pm 0.080\, \hbox {arcmin}, \varepsilon _{\omega }^{k_2 } =0.868\pm 0.034\, \hbox {arcsec}$ and $\varepsilon _\zeta =0.995 \pm 2.914\, \hbox {arcsec}$.

With the extended Cassini state model the realization of the extended dynamical reference system is possible. In this reference system the z-axis coincides exactly with rotation axis. Given the values for the precession and nutation amplitudes obtained by Baland et al. (2017) one obtains $W_0^{\mathrm{eCS}} =329.7372\pm 0.0053^{\circ }$ (the error bar is obtained through error propagation of uncertainties of the averaged orbital elements (Stark et al. 2015) and the obliquity (Baland et al. 2017)).

Appendix B: Hun Kal crater

Hun Kal is a simple impact crater located in a relatively rough terrain near to the equator of Mercury. In direct vicinity are two larger unnamed impact craters of 3 and 10 km diameter in the southeast and northwest directions, respectively (Fig. 1). All three craters are located on the crater floor of an older heavily degraded impact crater of about 40 km diameter.

Using Mariner 10 images Murray et al. (1974) reported a diameter 1.5 km for Hun Kal and proposed it for definition of the prime meridian of Mercury (see Sect. 3.1). However, the MESSENGER mission provided new images of Hun Kal which allow a more detailed assessment of the crater characteristics. We have identified in total 19 images of MDIS NAC and WAC, which are suitable for the analysis in terms of image resolution and quality. The images were ortho-rectified using a stereo DTM provided by Preusker et al. (2017) and resampled to a resolution of 10 m per pixel. Furthermore, we used the MESSENGER reference frame (Sect. 3.2) for the computation of the body-fixed coordinates. The diameter of Hun Kal was obtained by identifying the image pixels of the presumable crater rim in longitude and latitude directions (Table 4). Based on these measurements we also obtained the coordinates of the crater center. Using the image resolution and an indicator of the viewing quality of the crater as weights we compute average values for the diameter and the crater center coordinates. The results for the diameter of the crater in the longitude and latitude directions are consistent with the assumption of a circular crater rim. By combination of measurements in both directions we obtain a mean diameter of 1.402  ±  0.112 km. By computing the length of the shadow in images with low Sun elevation we roughly estimate the crater depth to about 340 m. The averaged value of the crater center location in the images is 0.4646 ±  0.0124$^{\circ }$S and 339.9930  ±  0.0153$^{\circ }$E. The small offset of 0.007$^{\circ }$ (300 m) from the 340$^{\circ }$E longitude is not significant and demonstrates that the computation of the prime meridian constant of the MESSENGER frame by Stark (2015) is compliant with the definition of Mercury’s prime meridian within the uncertainties of the data. The obtained values are also consistent with the Hun Kal coordinates obtained by Preusker et al. (2017) (Sect. 3.3).