1 Introduction

Since the outbreak of COVID-19, the literature about currency markets has tried to address the consequences of the pandemic on their functioning and reaction to policy interventions, and on the interdependence between currencies. In particular, Aloui (2021) studies the role of COVID-19 in altering the response of exchange rates to policy tools, while Aquilante et al. (2022) analyse the impact of news about Covid-19 on currencies. Furthermore, Narayan (2022) studies the spillover between exchange rates during the COVID-19 period, and Xu and Lien (2022) analyse the interdependence between currencies and COVID-19. Boubaker et al. (2021) show that the correlations between pairs of exchange rates significantly decreased during the COVID-19 outbreak. Finally, Mo et al. (2023) examine the interconnection and spillovers of G10 countries over the period 2018–2021 and conclude that, during the COVID-19 pandemic, countries with higher infection cases experience currency depreciation and transmit more currency risk to others. Related to currency risk, the response of exchange rates volatility to COVID-19 has only been scarcely analysed in the extant literature; see, for example, Feng et al. (2021), who consider the response of exchange rates volatility to COVID-19-related government interventions.

We contribute to this growing literature by analysing the interdependence of the volatility of exchange rates and whether it has changed after the COVID-19 pandemic. We consider a fractionally integrated multi-level dynamic factor model (FI-ML-DFM) designed to capture different levels of interdependence between a panel of hourly exchange rates realized volatilities. By exploiting the informative content of ultra-high frequency data, the model is capable of separating global factors, active along the twenty-four hours of the day, from intermittent factors that are only active over specific intra-daily time ranges, when markets in a given geographical area are active. A challenging aspect of the FI-ML-DFM considered is the identification of the optimal number of global-in-time factors. In fact, the misspecification of the number of global factors impacts on the possible identification of intermittent factors. We thus introduce a heuristic approach for the determination of the number of global factors based on analysing when a distance of the loadings of the intermittent factors picks.

The extraction of factors (in our case, both global and intermittent) has implications in various areas, from risk evaluation to forecasting. Our results would be relevant for risk spillover analysis, where we might replace a collection of exchange rates with global and intermittent factors, extending, in this way, the results of Wei et al. (2020) or Hsu et al. (2021). Furthermore, the extrapolation of global and intermittent factors from our model might also have interesting applications in the forecasting area. In the same vein, Brooks et al. (2022) identify a common factor in interest rates futures, and show that exchange rates are highly linked to this common factor. Our approach might help in shedding further light in this direction, for instance, by correlating the interest rate common factors with both the global and intermittent common factors of the volatilities of exchange rates. Similarly, Kwas et al. (2022) use exchange rates as a factor for the prediction of cereal prices, a potentially relevant topic given the early 2022 events while Jaworski (2021) focuses on the “exchange rate disconnect puzzle” and analyses the link between exchange rates and macroeconomic fundamentals in Central and Eastern European countries, obtaining predictions of exchange rates by taking advantage of the entire factor structure, using both global and country-specific factors.Footnote 1

In this paper, we show that although the bulk of common dynamics of exchange rates realized volatilities can be attributed to the global factors active over the day, there are non-negligible effects of factors active over the time zones. The effect of the COVID-19 on the comovements of the volatilities is different among factors. The strongest effect is observed on the first global-in-time factor, which shows a permanent increase in its level after the pandemic started. The second global factor and the intermittent factors active when the markets in the EU, UK and USA are operating, show smooth transitory increases in their levels that last for about one year since the pandemic starts. Finally, there are not effects of the pandemic neither on the third common factor nor on the intermittent factor active while the markets in Asia are open.

The paper proceeds as follows. Section 2 describes the data and the construction of realized volatilities. Section 3 introduces the FI-ML-DFM considered in this paper and describes the methodology proposed to identify the intermittent factors. Section 4 presents the empirical results. Finally, Sect. 5 concludes.

2 Database and construction of realized volatilities

To analyse the factor structure of exchange rates volatilities, we consider a set of 19 time series of ultra-high frequency exchange rates expressed in US dollars (USD); see Table 1 for the list of exchange rates considered and their acronyms. Note that Ilzetzki et al. (2021) show that the USD has become ever-more central as the de facto anchor for currencies for much of the world. The data, observed at the 1-minute frequency on a 24 h basis for five days a week, and recorded from 5 PM on Sunday up to 5 PM on Friday, at New York time stamp, have been recovered from Kibot.com, from the beginning of January 2010 up to the end of August 2021, for 3040 daysFootnote 2. The set of 19 exchange rates has been identified by focusing on floating exchange rates, on the illiquidity (as proxied by the number of zero returns at the 1-minute frequency) and on the absence of pegging or peculiar exchange rates regimes (IMF 2021)Footnote 3.

For each exchange rate, we construct hourly realized volatilities (RV), that is, the sum of squared 1-min returns observed within a given hour, obtaining 120 observations of RV per week; see Barndorff-Nielsen and Shephard (2002). Each series of RV is sequentially cleaned of seasonal effects and outliers. First, we filter the hourly time series from the periodic deterministic component characterizing their evolution; see Gencay et al. (2001) for the existence of periodicity in intra-daily time series.Footnote 4 In filtering the periodic component, we account for a seasonal oscillation with a length of 120 observations, that is, 1 week.

Table 1 Exchange rates against the USD and outliers (absolute and relative frequency)
Full size table

Second, we further clean the seasonally adjusted RV series from outliers and outlying series, which are identified using the procedures proposed by Galeano et al. (2006) and Alonso et al. (2020). Table 1 reports the frequency and percentage of identified outliers.Footnote 5 We further observe that the outliers might be associated with the occurrence of price jumps (which we did not filter out from our raw 1-min data), with a small frequency in line with those observed on liquid equity data (Caporin 2023).

The temporal dependence of each series of filtered hourly RVs is described in Fig. 1, which plots the corresponding sample autocorrelations for up to 480 lags. Notably, all series of RV show evidence of a strong serial dependence, which might be interpreted as supporting the existence of long-memory in RV sequences; see, for example, Christensen and Nielsen (2007), Nielsen (2007), Boubaker et al. (2021) and Wang et al. (2023) for evidence of long-memory in conditional variances of daily exchange rates.

Fig. 1
figure 1

Sample autocorrelations of filtered hourly RV sequences

Full size image

3 A multi-level dynamic factor model for realized volatilities

To capture the common dynamic evolution of the exchange rate RV sequences, we consider a FI-ML-DFM in which the unobserved factors are classified into Global-in-Time (GiT) factors, which are pervasive and affect all time zones along the day, and Local-in-Time (LiT) factors, which are non-pervasive and affect only a specific time zone, turning on and off depending on the time of day associated with trading hours of regional financial markets. In particular, we split the working day into four regimes: (i) from 8 AM to 2 PM when trading in EU/UK markets is active (5 h); (ii) from 2 to 5 PM when the EU/UK/US markets are trading (4 h); (iii) from 5 to 10 PM when only the US market is trading (4 h); (iv) the rest of the day when trading in Asia is active (9 h).

To simplify the model complexity, we assume that there are four LiT factors, with a single LiT factor active in each of the four time zones, while there could be r GiT factors. Let \(y_{it}\) be the RV of exchange rate i, \(i=1,\ldots , 19\), at time t, \(t=1,\ldots ,72960\). The FI-ML-DFM is given by

$$\begin{aligned} y_{it}=\gamma _{1i}G_{1t} + \gamma _{2i} G_{2t}+\cdots + \gamma _{ri} G_{rt}+\lambda _{1i}F_{1t}+\lambda _{2i}F_{2t} +\lambda _{3i}F_{3t}+\lambda _{4i}F_{4t}+\epsilon _{it}, \end{aligned}$$
(1)

where \(G_{kt}, k=1,\ldots ,r\) are the GiT factors, \(F_{jt}\), \(j=1,\ldots ,4\), are the LiT factors, and \(\gamma _{ki}\) and \(\lambda _{ji}\) are their corresponding factor loadings. LiT factors are defined in such a way that they are zero when the time zone is different from that for which they are active. Assume, for example, that the sample starts when the first regime is active, i.e. from 9 AM to 1 PM, when trading in EU/UK markets is operating. During these hours, \(F_{1t}\) turns on. Next, the sample passes to the second regime, from 1 to 5 PM, corresponding to the EU/UK/US trading region, with \(F_{1t}\) turning off and \(F_{2t}\) turning on. The same pattern repeats for the rest of LiT factors. Therefore, the LiT factors can be defined as \(F_{jt}=F^{*}_{jt} I_{jt}\), where \(I_{jt}\) is an indicator variable that takes value 1 when the j‘th time zone is active. Let \(y_{i,t_1}\) be the vector of observations of the i‘th currency related to the first time trading zone of the first day, \(y_{i,t_2}\) be the second sub-sample of observations belonging to the second time trading zone of the first day, and so on. Define analogously \(\epsilon _{i,t_1}\), \(\epsilon _{i,t_2}\),..., \(G^{\prime }_{t_1}=(G_{1,t_1}, G_{2,t_1},\ldots , G_{r,t_1})\), \(G^{\prime }_{t_2}\),...and \(F_{j,t_1}\), \(F_{j,t_2}\),..., for \(j=1,\ldots ,4\). Then, model (1) can be written as follows:

$$\begin{aligned} \left( \begin{array}{c} y_{i,t_1} \\ y_{i,t_2} \\ y_{i,t_3} \\ y_{i,t_4} \\ y_{i,t_5} \\ y_{i,t_6} \\ \vdots \end{array} \right) =\left( \begin{array}{ccccc} G_{\textrm{t}_{1}}^{\prime } &{}\quad F_{1, \textrm{t}_{1}}^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ G_{\textrm{t}_{2}}^{\prime } &{}\quad 0 &{}\quad F_{2, \textrm{t}_{2}}^{\prime } &{}\quad 0 &{}\quad 0 \\ G_{\textrm{t}_{3}}^{\prime } &{}\quad 0 &{}\quad 0&{}\quad F_{3, \textrm{t}_{3}}^{\prime } &{}\quad 0\\ G_{\textrm{t}_{4}}^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad F_{4, \textrm{t}_{4}}^{\prime } \\ G_{\textrm{t}_{5}}^{\prime } &{}\quad F_{1, \textrm{t}_{5}}^{\prime } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ G_{\textrm{t}_{6}}^{\prime } &{}\quad 0 &{}\quad F_{2, \textrm{t}_{6}}^{\prime } &{}\quad 0 &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \end{array}\right) \left( \begin{array}{c} \gamma _{i} \\ \lambda _{1i} \\ \lambda _{2i}\\ \lambda _{3i}\\ \lambda _{4i} \end{array}\right) +\left( \begin{array}{c} \epsilon _{i,t_1} \\ \epsilon _{i,t_2} \\ \epsilon _{i,t_3} \\ \epsilon _{i,t_4}\\ \epsilon _{i,t_5}\\ \epsilon _{i,t_6} \\ \vdots \end{array}\right) , \end{aligned}$$
(2)

where \(\gamma _i=(\gamma _{1i}, \gamma _{2i},\ldots ,\gamma _{ri})^{\prime }\).

By restricting the factors, it is easier to attach an economic interpretation to them. GiT factors drive the commonality among all RV of exchange rates disregarding the time trading zone. However, there is a further commonality that only belongs to a specific trading zone and, therefore, to particular markets. The commonality in the volatilities due to intermittent factors is not attributed to the particular exchange rate (that can be traded in different markets along the day) but to the specific market functioning at each time-zone during the day.

Finally, in model (1), \(\epsilon _{it}\) are the idiosyncratic components, which are assumed to be serially uncorrelated and homoscedastic although they may have weak cross-sectional dependences. Coherently with the empirical evidence in the previous section, we allow for long-range dependence in model (1). Henceforth, \(G_{kt}=\Delta _{t}^{-\delta _k}w_{kt}\), \(F^{*}_{jt}=\Delta _{t}^{-\vartheta _{j}}v_{jt}\), and \(\epsilon _{it}=\Delta _{t}^{-d_{i}}u_{it}\), where \(w_{kt}, v_{jt}\), and \(u_{it}\) are stationary processes, and the operator \(\Delta _{t}^{-\zeta }\) introduces a type-II fractional process; see Davidson and Hashimzade (2009) for a complete technical explanation.

The FI-ML-DFM in (2) is close to the fractionally integrated ML-DFMs recently proposed by Ergemen and Rodríguez-Caballero (2023). However, these latter authors consider the traditional specification of the ML-DFM, with the factor loadings restricted for different blocks, while the proposed model imposes blocks of zero restrictions on the fractionally integrated factors instead of imposing zero restrictions on the factor loadings as in traditional ML-DFMs. Our model is also close to those fitted by Chiappini and Lahet (2020) and Jaworski (2021), who model exchange rate variations across countries by assuming a stationary ML-DFM with a global common factor, and regional and/or country-specific factors. In these models, the loadings are also restricted as in traditional DFMs and the factors are not assumed to be fractionally integrated. Our proposal is also different from that of Lustig et al. (2011), who focus on portfolios of currencies, which are formed on the basis of the size of the forward discount, and the currency returns are obtained as differentials between the forward at time t and the spot at time \(t+1\). Portfolio composition is rebalanced, as in traditional Fama–French portfolio construction, with the factors being identified on portfolios and not on single currencies. A last related model is that proposed by Breitung and Eickmeier (2015), who model comovements of macroeconomic variables by restricting the factors instead of the loadings, estimating factors that are common to all periods as well as phase-specific factors that drive the variables in recession or expansion phases only. Their specification is similar to that of model (1) except that they do not assume fractional integration of the factors.

For what concerns estimation of the FI-ML-DFM in (1), we start by estimating the integration order of each of the series of RVs using the extended Local Whittle (ELW) estimator of Abadir et al. (2007). The number of Fourier frequencies used is \(T^{0.75} = 4439\). After fractionally differencing each of the RV series using \(\bar{\hat{d}}\), the average of the estimated fractional parameters, a challenging aspect is the identification of the optimal number of GiT factors present in the data. For this goal, one can use one of the many criteria available in the literature related to the determination of the number of factors in DFMs; see, for example, the survey by Barhoumi et al. (2013). However, different criteria may determine different number of GiT factors. In fact, the misspecification of the number of global factors impacts on the possible identification of intermittent factors. We thus introduce a heuristic approach for the determination of the number of GiT factors focusing on the estimation of the LiT factors. First, we start by fixing the number of GiT factors to \(r=1\) and estimate model (1). If the distance between the zone-specific eigenvectors of the LiT factors obtained after filtering the first global factor is not large enough, it implies that there is a second GiT factor. Consequently, model (1) is estimated with \(r=2\) GiT factors. This procedure is iterated until the distance between the zone-specific loadings picks and/or the percentage of the explained variability is not increasing by adding more factors.

For each value of r in the iterative procedure described above, the parameters and underlying factors are estimated using the sequential least squares (LS) estimator proposed by Breitung and Eickmeier (2015). First, starting with initial estimates of the factor loadings obtained using canonical correlation analysis, the factors are estimated from the cross-sectional regressions in (2) with the loadings treated as regressors. Second, after transforming the estimated factors to be orthonormal, updated estimates of the loadings are obtained from the \(N=19\) time series regressions with the factors treated as regressors. The resulting iterative procedure results in a non-increasing sequence of the sum of squared residuals that eventually converges to the minimum. These regressions are iterated until convergence.Footnote 6

Finally, in the last step of the estimation procedure, the estimated GiT and LiT factors are integrated back by \(\bar{\hat{d}}\).

4 Empirical evidence

As described above, we start by estimating the fractional integration parameter for each series of realized volatilities described in Sect. 2. Figure 2, which plots the estimated \(\hat{d}_i\), shows that most of them imply stationarity. The average estimate of the fractional difference parameters is \(\bar{\hat{d}}= 0.46\).

Fig. 2
figure 2

Estimated fractional difference parameters for the filtered RVs and for the idiosyncratic components

Full size image

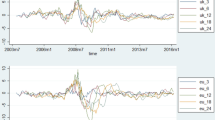
After transforming each realized volatility series by \(\bar{\hat{d}}= 0.46\), the number of GiT factors is determined using the criteria proposed by Ahn and Horenstein (2013) that determine \(r=1\) when the ER criterion is used, while \(r=3\) when using the GR criterion. Alternatively, we also use the criteria proposed by Onatski (2009) and Alessi et al. (2010), all of them choosing \(r=1\). Consequently, we start by assuming that \(r=1\) and estimate the FI-ML-DFM in (2) using the two-step procedure described above. The estimated GiT and LiT common factors of the RVs of the 19 exchange rates considered are plotted in Fig. 3 together with their corresponding loadings. We can observe that the loadings of the LiT factors are rather similar, suggesting that they are estimating a second GiT factor; see Fig. 4, which plots the difference between the largest and smallest LiT loadings for each currency.

Consequently, we estimate the FI-ML-DFM with \(r=2\), obtaining similar conclusions. The differences between the LiT loadings are still too small; see Fig. 4.

Fig. 3
figure 3

Estimated factors and their corresponding loadings

Full size image

Our final specification allows for \(r=3\) GiT factors (note that this is the number of factors chosen by the GR criterion of Ahn and Horenstein (2013)). Figure 4 shows that the differences between the largest and smallest LiT loadings pick for most currencies when \(r=3\).

Fig. 4
figure 4

Differences between the largest and smallest loadings of LiT factors for each currency for different number of GiT factors

Full size image

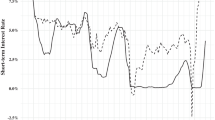
Figure 5 plots the estimated three GiT and four LiT factors together with their corresponding estimated loadings. Note that all exchange rates have positive loadings on this common factor but the Argentinian peso, which volatility seems not to be affected by the first GiT factor. Therefore, the first GiT factor can be interpreted as an overall volatility common to all markets. The dynamic evolution of the first GiT factor shows a decreasing pattern up to July 2014, when a first increase takes place. This is located in the correspondence of the FED tapering and the appreciation of the USD against other currencies. After the increase, ended in January 2015, the trend reverts with a decreasing pattern until the COVID-19 outbreak; see Ilzetzki et al. (2021), who explore the evolution of the global exchange rate system and mention “the surprising recent trend decline in volatility of exchange rates at the core of the system”. According to Ilzetzki et al. (2021), the main drivers of the decline of currency volatility since 2014 have likely been a benign environment for exchange rate fluctuations, including low inflation and low interest rate volatility. The pandemic generates a very sharp spike on the commonality of the analysed exchange rates volatilities. This increase has been followed by a reversion towards lower levels. However, note that the pre-pandemic levels of this common volatility has not been reached by the end of the sample period. In August 2021, the common global volatility is still larger than before the COVID-19 outbreak.

Fig. 5
figure 5

Estimated factors and their corresponding loadings

Full size image

When looking at the estimated loadings of the second GiT factor, we can observe that it has positive weights in all currencies but those corresponding to European countries not yet integrated in the euro area, namely CZK, DKK, HUF and PLN. Note that CHF and SEK have weights very close to zero. The second GiT factor represents three regimes of exchange rates volatility. During the first one, until 2014, the volatility moves randomly around a constant level. From 2014 to 2016, they show an upward trend, and since then the level is moving randomly around a constant level higher than the previous one. After the COVID-19 outbreak, the second GiT factor shows a slight and transitory increase in the level of volatility.

The third GiT factor loads positively in CZK and HUF, while the loads are negative and large in ARG and THB currencies. This last third GiT factor has been increasing since 2015 and does not show any effect of the COVID-19 pandemic.

It is remarkable that there is a non-negligible contribution of the LiT factors to the volatility of exchange rates. This contribution is large for all currencies; see Fig. 6, which plots the coefficients of determination, \(R^2\), of the model in (1), decomposed into the contribution of the GiT and LiT factors. The first three LiT factors, active when the EU, UK and US markets are operating, can be described by a local level evolution with a sharp decrease around July 2016. The COVID-19 pandemic generated an increase in this intermittent common volatility that has been reverting since then. However, the COVID-19 does not have any remarkable effect on the factor active, while the markets in Asia are open.

Finally, with respect to the idiosyncratic components, we should mention that their fractional integration parameters are smaller than those of the original RV series in all cases but one and always imply stationarity; see Fig. 2. This indicates a fractional cointegration relationship between the original RV and the most persistent GiT factor (the first one).

Fig. 6
figure 6

Contributions to the \(R^2\) of GiT and LiT factors

Full size image

5 Conclusions

In this paper, we propose modelling the commonalities among exchange rates realized volatilities by a FI-ML-DFM in which the common factors are fractionally integrated with some of them being active during the twenty-four hours of the day, while other are active at mutually exclusive times that are determined according to different markets around the world being open. We also propose a methodology to determine the number of global-in-time factors based on finding when a distance between the loadings of the intermittent factors picks.

After fitting the proposed model to a system of realized volatilities of 19 currencies, our findings suggest that while the GiT factors have a relevant role, coherently with the expectation, the LiT factors might provide additional insights on the exchange rate volatility movements. These results can be relevant for risk spillover analysis or for forecasting variables that depend on the volatility of exchange rates. Further studies on the possible use of our modelling approach in risk management and volatility trading are thus needed.

The effect of the COVID-19 on the comovements of realized volatilities of exchange rates is stronger on the first global-in-time factor, which shows a permanent increase in the level. The effects on the second global-in-time and on the intermittent factors active when the EU, UK and US markets are operating are transitory, lasting for approximately a year after the COVID-19 outbreak. Finally, we cannot observe any effect of the COVID-19 pandemic neither on the third common global factor nor on the intermittent factor active, while the markets in Asia are operating.