A difference-based method for testing no effect in nonparametric regression

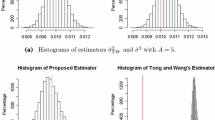
Abstract

The paper proposes a novel difference-based method for testing the hypothesis of no relationship between the dependent and independent variables. We construct three test statistics for nonparametric regression with Gaussian and non-Gaussian random errors. These test statistics have the standard normal as the asymptotic null distribution. Furthermore, we show that these tests can detect local alternatives that converge to the null hypothesis at a rate close to $n^{-1/2}$ previously achieved only by the residual-based tests. We also propose a permutation test as a flexible alternative. Our difference-based method does not require estimating the mean function or its first derivative, making it easy to implement and computationally efficient. Simulation results demonstrate that our new tests are more powerful than existing methods, especially when the sample size is small. The usefulness of the proposed tests is also illustrated using two real data examples.

Appendices

Appendix 1: Some lemmas and their proofs

Lemma 1

Assume that $m \rightarrow \infty$ and $m = o(n)$. We have

• (a) $\sum _{k=1}^{m}h_k= \frac{15}{16}n+o(n)$;

• (b) $\sum _{k=1}^{m} k^2 h_k = n^2m +o(n^2m)$;

• (c) $\sum _{k=1}^{i-1}h_k= \frac{15n^2}{4\,m^4}(i^3 - m^2i) + O\big (\frac{n^2}{m^2}\big ) + o\big (\frac{n^2i}{m^2}\big )$;

• (d) $\sum _{k=i}^{m}k h_k= O(n^2)$;

• (e) $\sum _{k=1}^{i-1} k^2 h_k = O(\frac{n^2i^3}{m^2})$;

• (f) $\sum _{k=1}^{m}h_k^2 = \frac{45n^4}{4m^3} +o(\frac{n^4}{m^3})$;

• (g) $\sum _{k=1}^{m}k h_k^2 = \frac{225n^4}{32m^2} +o(\frac{n^4}{m^2})$.

Proof

Following the Appendix in Tong and Wang (2005), we have

$$\begin{aligned} \sum _{k=1}^{m} (d_k -\bar{d}_w)&= \frac{m^4}{12n^3} + o\Big (\frac{m^4}{n^3}\Big ), \end{aligned}$$

(A1)

$$\begin{aligned} \sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2&= \frac{4m^4}{45n^4} + o\Big (\frac{m^4}{n^4}\Big ), \end{aligned}$$

(A2)

$$\begin{aligned} \bar{d}_w&= \frac{m^2}{3n^2}+ o\Big (\frac{m^2}{n^2}\Big ). \end{aligned}$$

(A3)

• (a) By (A1) and (A2), we have

  $$\begin{aligned} \sum _{k=1}^{m} h_k&= \frac{\sum _{k=1}^{m} (d_k -\bar{d}_w)}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} = \frac{\frac{m^4}{12n^3} + o(\frac{m^4}{n^3})}{\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})} = \frac{15n}{16} +o(n). \end{aligned}$$

• (b) By (A2) and (A3), we have

  $$\begin{aligned} \sum _{k=1}^{m} k^2 h_k&= \frac{\sum _{k=1}^{m} k^2(d_k -\bar{d}_w)}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} = \frac{\frac{4m^5}{45n^2} + o\big (\frac{m^5}{n^2}\big )}{\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})} = n^2m +o(n^2m), \end{aligned}$$

  where

  $$\begin{aligned} \sum _{k=1}^{m} k^2(d_k -\bar{d}_w)&= \frac{1}{n^2} \Big (\frac{m^5}{5} + O(m^4)\Big ) - \Big (\frac{m^3}{3} +O(m^2)\Big )\Big [\frac{m^2}{3n^2} + o\Big (\frac{m^2}{n^2}\Big )\Big ] \\&= \frac{4m^5}{45n^2} + o\Big (\frac{m^5}{n^2}\Big ). \end{aligned}$$

• (c) For $1 \le i \le m$, by (A2) and (A3) we have

  $$\begin{aligned} \sum _{k=1}^{i-1}h_k&= \frac{\sum _{k=1}^{i-1}(d_k -\bar{d}_w)}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} \\&= \frac{ \frac{1}{3n^2}(i^3 - m^2i) +O\big (\frac{m^2}{n^2}\big ) +o\big (\frac{m^2i}{n^2}\big )}{\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})} \\&= \frac{15n^2}{4m^4}(i^3 - m^2i) + O\Big (\frac{n^2}{m^2}\Big ) + o\Big (\frac{n^2i}{m^2}\Big ), \end{aligned}$$

  where

  $$\begin{aligned} \sum _{k=1}^{i-1}(d_k -\bar{d}_w) = \sum _{k=1}^{i-1} (\frac{k}{n})^2 - (i-1)\bar{d}_w = \frac{1}{3n^2}(i^3 - m^2i) +O\Big (\frac{m^2}{n^2}\Big ) +o\Big (\frac{m^2i}{n^2}\Big ). \end{aligned}$$

• (d) For $1\le i \le m$, by (A2) we have

  $$\begin{aligned} \sum _{k=i}^{m}k h_k&= \frac{\sum _{k=i}^{m} k(d_k -\bar{d}_w)}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} =\frac{\sum _{k=i}^{m} \frac{k^3}{n^2} - \bar{d}_w \sum _{k=i}^{m}k}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} = O(n^2). \end{aligned}$$

• (e) For $1\le i \le m$, by (A2) we have

  $$\begin{aligned} \sum _{k=1}^{i-1} k^2 h_k&= \frac{\sum _{k=1}^{i-1} k^2(d_k -\bar{d}_w)}{\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2} \\&= \frac{\frac{1}{n^2}(\frac{i^5}{5}+O(i^4)) - [\frac{m^2}{3n^2} + o(\frac{m^2}{n^2})][\frac{i^3}{3}+O(i^2)] }{\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})}\\&= O\Big (\frac{n^2i^3}{m^2}\Big ). \end{aligned}$$

• (f) By (A2), we have

  $$\begin{aligned} \sum _{k=1}^{m} h_k^2&=\frac{\sum _{k=1}^{m} (d_k -\bar{d}_w)^2}{(\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2)^2}\\&= \frac{\sum _{k=1}^{m}d_k^2 -2\bar{d}_w\sum _{k=1}^{m}d_k+m(\bar{d}_w) ^2}{(\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2)^2}\\&= \frac{\frac{m^5}{n^4}(\frac{1}{5} -\frac{2}{9}+\frac{1}{9} ) +o(\frac{m^5}{n^4})}{[\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})]^2}\\&= \frac{45n^4}{4m^3} + o\Big (\frac{n^4}{m^3}\Big ). \end{aligned}$$

• (g) By (A2), we have

  $$\begin{aligned} \sum _{k=1}^{m} k h_k^2&=\frac{\sum _{k=1}^{m} k(d_k -\bar{d}_w)^2}{(\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2)^2}\\&= \frac{\sum _{k=1}^{m}kd_k^2 -2\bar{d}_w\sum _{k=1}^{m}kd_k+(\bar{d}_w) ^2\sum _{k=1}^{m}k}{(\sum _{k=1}^{m} w_k (d_k - \bar{d}_w)^2)^2}\\&= \frac{\frac{m^6}{n^4}(\frac{1}{6} -\frac{1}{6}+\frac{1}{18} ) +o(\frac{m^6}{n^4})}{[\frac{4m^4}{45n^4} + o(\frac{m^4}{n^4})]^2}\\&= \frac{225n^4}{32m^2} + o\Big (\frac{n^4}{m^2}\Big ). \end{aligned}$$

$\square$

Lemma 2

Assume that $m \rightarrow \infty$ and $m=o(n)$, and let $\textbf{g} = (g(x_1), \dots , g(x_n))^T$. We have

• (a) $\textbf{g}^T \varvec{B} \textbf{g} = 2\beta mn+O(m^2)$;

• (b) $\textbf{g}^T \varvec{B}^2\textbf{g} = O(n^2m)$.

Proof

• (a) Let $\varvec{A}= (a_{ij})_{n\times n}$ be a symmetric matrix with $a_{ij}$ having the same form as $b_{ij}$ in (7) but $h_0 = 0$ and $h_k = 1$ for $k = 1, \dots , m$. Let $\varvec{D} = (d_{ij})_{n\times n}$ is the matrix defined in Theorem 1 of Tong and Wang (2005). Then,

  $$\begin{aligned} {\textbf {g}}^T \varvec{B} {\textbf {g}} = \frac{{\textbf {g}}^T (\varvec{A}-\varvec{D}) {\textbf {g}}}{\bar{d}_w}. \end{aligned}$$

  To simplify the notation, we let $g_i=g(x_i)$. We can show that

  $$\begin{aligned} {\textbf {g}}^T \varvec{A} {\textbf {g}}&= \sum _{k=1}^{m}\sum _{i=1}^{n-k} (g_{i+k} - g_i)^2\\&=\sum _{k=1}^{m}\sum _{i=1}^{n-k} \Big [\frac{k^2}{n^2}(g_i')^2 + O\Big (\frac{k^3}{n^3}\Big ) \Big ]\\&=\sum _{k=1}^{m} \frac{k^2}{n^2} \sum _{i=1}^{n-k}(g_i')^2 + \sum _{k=1}^{m} O\Big (\frac{(n-k)k^3}{n^3}\Big )\\&=\sum _{k=1}^{m} \frac{k^2}{n} \Big [\frac{1}{n}\sum _{i=1}^{n}(g_i')^2 - \frac{1}{n}\sum _{i=n-k+1}^{n}(g_i')^2\Big ] + O\Big (\frac{m^4}{n^2}\Big )\\&=\sum _{k=1}^{m} \frac{k^2}{n} \Big [2\beta +O\Big (\frac{k}{n}\Big )\Big ] +O\Big (\frac{m^4}{n^2}\Big )\\&= \frac{2\beta m^3}{3n} +O\Big (\frac{m^4}{n^2}\Big ), \end{aligned}$$

  where $\beta = \int _{0}^{1} (g'(x))^2 \, dx/2$. Note also that ${\textbf {g}}^T \varvec{D} {\textbf {g}} = O(m^4/n^2)$ by Lemma 2 in Tong et al (2013). Then by (A3), we have

  $$\begin{aligned} {\textbf {g}}^T \varvec{B} {\textbf {g}} = \frac{\frac{2\beta m^3}{3n}+ O(\frac{m^4}{n^2})}{\frac{m^2}{3n^2} + o(\frac{m^2}{n^2})} = 2\beta mn+O(m^2). \end{aligned}$$

• (b) Noting that $\varvec{B}$ is a symmetric matrix, we let ${\textbf {g}}^T \varvec{B}^2 {\textbf {g}} = (\varvec{B}{} {\textbf {g}})^T (\varvec{B}{} {\textbf {g}}) = \varvec{q}^T \varvec{q}$, where $\varvec{q} = \varvec{B}{} {\textbf {g}} = (q_1, \dots , q_n)^T$. For $i \in [1,m]$, by parts (b), (d) and (e) of Lemma 1, we have

  $$\begin{aligned} q_i&= \sum _{k=1}^{i-1}h_k (g_i - g_{i-k}) - \sum _{k=1}^{m}h_k (g_{i+k} - g_{i})\\&=\sum _{k=1}^{i-1}h_k \Big (\frac{k}{n}g_i' -\frac{k^2}{2n^2}g_i''+o\big (\frac{k^2}{n^2}\big )\Big ) - \sum _{k=1}^{m}h_k \Big (\frac{k}{n}g_i' +\frac{k^2}{2n^2}g_i''+o\big (\frac{k^2}{n^2}\big )\Big )\\&= -\frac{g_i'}{n}\sum _{k=i}^{m}k h_k - \Big [\frac{g_i''}{2n^2}\big (\sum _{k=1}^{i-1}k^2h_k+ \sum _{k=1}^{m}k^2h_k\big )\Big ]+o\Big (\frac{1}{n}\sum _{k=i}^{m}k^2h_k \Big )\\&= O(n)+O(m)+O\Big (\frac{i^3}{m^2}\Big ) +o(m)\\&= O(n). \end{aligned}$$

  Similary, we can show that $q_i=O(n)$ for $i \in [n-m+1,n]$. While for $i \in [m+1,n-m]$, by Lemma 1(b) we have

  $$\begin{aligned} q_i&= \sum _{k=1}^{m}h_k (g_i - g_{i-k}) - \sum _{k=1}^{m}h_k (g_{i+k} - g_{i})\\&= \sum _{k=1}^{m}h_k \Big (\frac{k}{n}g_i' -\frac{k^2}{2n^2}g_i''+o\Big (\frac{k^2}{n^2}\Big )\Big ) - \sum _{k=1}^{m}h_k \Big (\frac{k}{n}g_i' +\frac{k^2}{2n^2}g_i''+o\Big (\frac{k^2}{n^2}\Big )\Big )\\&= -\frac{1}{n^2}g_i''\sum _{k=1}^{m}k^2h_k+o\Big (\frac{\sum _{k=1}^{m}k^2h_k}{n^2}\Big )\\&= O(m). \end{aligned}$$

  Taken together the above results, it yields that

  $$\begin{aligned} {\textbf {g}}^T\varvec{B}^2{\textbf {g}} = \sum _{i=1}^{m} q_{i}^{2}+\sum _{i=m+1}^{n-m} q_{i}^{2}+\sum _{i=n-m+1}^{n} q_{i}^{2} = O(n^2m). \end{aligned}$$

$\square$

Lemma 3

Assume that $m \rightarrow \infty$ and $m = o(n)$. We have

• (a) $\sum _{i=1}^{n}b_{ii}^2= \frac{15n^4}{14m}+ o(\frac{n^4}{m})$;

• (b) $\sum _{i=1}^{n}\sum _{j=1,j\ne i}^{n} b_{ij}^2=\frac{45n^5}{2\,m^3} + o(\frac{n^5}{m^3})$.

Proof

• (a) By parts (a) and (c) of Lemma 1, we have

  $$\begin{aligned} \sum _{i=1}^{n}b_{ii}^2&= 2\sum _{i=1}^{m}\big (\sum _{k=1}^{m}h_k +\sum _{k=1}^{i-1}h_k\big )^2 + \sum _{i=m+1}^{n-m}\big (2 \sum _{k=1}^{m} h_k\big )^2 \\&=2\sum _{i=1}^{m}\Big [\frac{15}{16}n+o(n)+ \frac{15n^2}{4m^4}(i^3 - m^2i) + O\Big (\frac{n^2}{m^2}\Big ) + o\Big (\frac{n^2i}{m^2}\Big )\Big ]^2 \\&\qquad + 4(n-2m)\Big [\frac{15}{16}n+o(n)\Big ]^2\\&= 2\Big (\frac{15}{16}\Big )^2n^2m + \Big (\frac{15n^2}{4m^4}\Big )^2\Big (\sum _{i=1}^{m} i^6 + m^4\sum _{i=1}^{m}i^2-2m^2\sum _{i=1}^{m}i^4\Big ) \\&\qquad + \frac{15^2n^3}{32m^4}\Big (\sum _{i=1}^{m}i^3 - m^2\sum _{i=1}^{m}i\Big ) + o\Big [\frac{n^4}{m^6}\Big (\sum _{i=1}^{m}i^4-m^2\sum _{i=1}^{m}i^2\Big ) \Big ]\\&\qquad +4\Big [\Big (\frac{15}{16}\Big )^2 n^3+o(n^3) \Big ]\\&= \frac{15n^4}{14m}+o\Big (\frac{n^4}{m}\Big ). \end{aligned}$$

• (b) By parts (f) and (g) of Lemma 1, we have

  $$\begin{aligned} \sum _{i=1}^{n}\sum _{j=1,j\ne i}^{n} b_{ij}^2&= 2 \sum _{k=1}^{m}(n-k)h_k^2\\&=2n\Big [ \frac{45n^4}{4m^3} +o\Big (\frac{n^4}{m^3}\Big ) \Big ] -2\Big [\frac{225n^4}{32m^2} +o\Big (\frac{n^4}{m^2}\Big )\Big ]\\&= \frac{45n^5}{2m^3}+o\Big (\frac{n^5}{m^3}\Big ). \end{aligned}$$

$\square$

Appendix 2: Proof of Theorem 1

Proof

Let ${\textbf {g}} = (g(x_1), \dots , g(x_n))^T$ and $\varvec{\epsilon } = (\epsilon _1, \dots , \epsilon _n)^T$. By (1) and (6), we have

$$\begin{aligned} \hat{\beta }= \frac{{\textbf {g}}^T \varvec{B} {\textbf {g}}}{2N} + \frac{{\textbf {g}}^T \varvec{B} \varvec{\epsilon }}{N}+\frac{\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }}{2N}. \end{aligned}$$

From Lemma 2(a) we have

$$\begin{aligned} \frac{{\textbf {g}}^T \varvec{B} {\textbf {g}}}{2N} = \frac{2\beta mn+O(m^2)}{2N} =\beta + O\Big (\frac{m}{n}\Big ). \end{aligned}$$

Using Lemma 2(b), we have ${{E}}({\textbf {g}}^T \varvec{B} \varvec{\epsilon } /N)^2 = \sigma ^2 {\textbf {g}}^T \varvec{B}^2{\textbf {g}}/N^2 = O(1/m)$. This leads to

$$\begin{aligned} \frac{{\textbf {g}}^T \varvec{B} \varvec{\epsilon }}{N} = O_p\Big (\frac{1}{\sqrt{m}}\Big ). \end{aligned}$$

Let $\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }/(2N) = \varvec{\epsilon }^T \varvec{C} \varvec{\epsilon } - \varvec{\epsilon }^T \varvec{U} \varvec{\epsilon }$, where the elements of matrix $\varvec{C}$ are

$$\begin{aligned} c_{ij} = {\left\{ \begin{array}{ll} \sum _{k=1}^{m}h_k/N, &{} 1\le i = j \le n, \\ -h_{|i-j|}/(2N), &{} 0 < |i-j| \le m, \\ 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

and $\varvec{U}=\textrm{diag}(u_1, \cdots , u_n)$ with $u_i = \sum _{k=min\{i,n+1-i,m+1\} }^{m+1} h_k/(2N)$, for $i = 1, \dots , n$ and $h_{m+1} = 0$. Let $c_0 = \sum _{k=1}^{m}h_k/N$, $c_{i-j} = c_{j-i} = -h_{|i-j|}/(2N)$ for $1 \le |i-j| \le m$, and $c_{i-j} = c_{j-i} = 0$ for $|i-j| >m$. Then $\varvec{\epsilon }^T \varvec{C} \varvec{\epsilon } = \sum _{i=1}^{n}\sum _{j=1}^{n} c_{i-j} \epsilon _i \epsilon _j$, where $\epsilon _i$ are i.i.d. with mean zero. Thus by parts (a) and (f) of Lemma 1,

$$\begin{aligned} \sum _{-\infty }^{\infty } c_k^2 = \frac{(\sum _{k=1}^{m}h_k)^2}{N^2} + 2\sum _{k=1}^{m} \frac{h_k^2}{4N^2} =\frac{O(n^2)}{O(n^2m^2)} + \frac{O(n^4/m^3)}{O(n^2m^2)} = O\Big (\frac{1}{m^2}\Big )+O\Big (\frac{n^2}{m^5}\Big ) < \infty , \end{aligned}$$

as $m = \lceil n^r\rceil$ with $2/5 \le r<1$. Assuming $E(\epsilon ^6) < \infty$, by Theorem 2 in Whittle (1962), $\varvec{\epsilon }^T \varvec{C} \varvec{\epsilon }$ is asymptotically normally distributed.

We have $\varvec{\epsilon }^T \varvec{U} \varvec{\epsilon } = \sum _{i=1}^{n} u_i \epsilon _i^2$. Let $X_i = u_i \epsilon _i^2$, then $X_1, X_2, \dots , X_n$ are independent random variables, where $X_i = \sum _{k=i}^{m} h_k \epsilon _i^2/(2N)$ for $1 \le i \le m$, $X_i = \sum _{k=n-i+1}^{m} h_k \epsilon _i^2/(2N)$ for $n-m+1 \le i \le n$, and $X_i = 0$ for $m+1 \le i \le n-m$. For $1 \le i \le m$, using parts (a) and (c) of Lemma 1 we have

$$\begin{aligned} {{E}}[X_i]&= \frac{\sigma ^2}{2N} \sum _{k=i}^{m}h_k = \frac{\sigma ^2}{2N} \Big (\sum _{k=1}^{m}h_k - \sum _{k=1}^{i-1}h_k\Big )\\&= \frac{15\sigma ^2}{8}\Big (\frac{1}{4m} - \frac{ni^3}{m^5} + \frac{ni}{m^3}\Big ) +O\Big (\frac{n}{m^3}\Big )+o\Big (\frac{1}{m}\Big ) +o\Big (\frac{ni}{m^3}\Big ) <\infty , \end{aligned}$$

as $m = \lceil n^r\rceil$ with $1/2< r<1$. For $n-m+1 \le i \le n$, the results are similar. It is intuitive to show that for $1 \le i \le m$, the variance of $X_i$ is

$$\begin{aligned} \text {Var}(X_i)&= {{E}}(X_i^2) -{{E}}(X_i)^2 = \Big (\frac{\sum _{k=i}^{m}h_k}{2N}\Big )^2[{{E}}(\epsilon _i^4) - \sigma ^4]\\&= (\gamma _4 - 1)\sigma ^4 \Bigg [\frac{15}{8}\Big (\frac{1}{4m} - \frac{ni^3}{m^5} + \frac{ni}{m^3}\Big ) +O\Big (\frac{n}{m^3}\Big )+o\Big (\frac{1}{m}\Big ) +o\Big (\frac{ni}{m^3}\Big )\Bigg ]^2 < \infty , \end{aligned}$$

as $n \rightarrow \infty$ and $m = \lceil n^r\rceil$ with $1/2< r<1$. We have similar results for $n-m+1 \le i \le n$, and $\text {Var}(X_i) = 0$ for $m+1 \le i \le n-m$. Noting also that $\sum _{i=1}^{m} \text {Var}(X_i) = \sum _{i=n-m+1}^{n} \text {Var}(X_i)$, we can derive the sum of variance as

$$\begin{aligned} s_n^2&= \sum _{i=1}^{n} \text {Var}(X_i) = 2\sum _{i=1}^{m} \text {Var}(X_i)\\&= 2(\gamma _4 - 1)\sigma ^4 \sum _{i=1}^{m} \Bigg [\frac{15}{8}\Big (\frac{1}{4m} - \frac{ni^3}{m^5} + \frac{ni}{m^3}\Big ) +O\Big (\frac{n}{m^3}\Big )+o\Big (\frac{1}{m}\Big ) +o\Big (\frac{ni}{m^3}\Big )\Bigg ]^2\\&= 2(\gamma _4 - 1)\sigma ^4 \Big [\frac{225}{64}\sum _{i=1}^{m}\Big (\frac{1}{16m^2} + \frac{n^2i^6}{m^{10}} + \frac{n^2i^2}{m^6}-\frac{ni^3}{2m^6} + \frac{ni}{2m^4} - \frac{2n^2i^4}{m^8} \Big ) + o\Big (\frac{n^2}{m^3}\Big ) \Big ]\\&= 2(\gamma _4 - 1)\sigma ^4 \cdot \frac{225}{64}\Big (\frac{1}{7}+\frac{1}{3}-\frac{2}{5}\Big )\frac{n^2}{m^3}+o\Big (\frac{n^2}{m^3}\Big )\\&= \frac{15}{28}(\gamma _4 - 1)\sigma ^4\frac{n^2}{m^3}+o\Big (\frac{n^2}{m^3}\Big ). \end{aligned}$$

Thus $s_n^2$ is finite as $m = \lceil n^r\rceil$ with $2/3 \le r<1$. Moreover, we have

$$\begin{aligned} \sum _{i=1}^{n} {{E}}\big [|X_i - \mu _i|^3\big ]&=2\sum _{i=1}^{m}{{E}}\Big [\Big |\frac{\sum _{k=i}^{m}h_k}{2N}(\epsilon _i^2-\sigma ^2) \Big |^3 \Big ]\\&=2\sum _{i=1}^{m}\Big (\frac{\sum _{k=i}^{m}h_k}{2N}\Big )^3 E\big [|\epsilon _i^2-\sigma ^2|^3\big ]\\&=\tau _0 \sum _{i=1}^{m} \Big [O\Big (\frac{1}{m} \Big ) +O\Big (\frac{ni^3}{m^5} \Big )+O\Big (\frac{ni}{m^3} \Big ) \Big ]^3\\&=O\Big (\frac{1}{m^2}\Big ) +O\Big (\frac{n^3}{m^5} \Big ) = O\Big (\frac{n^3}{m^5} \Big ), \end{aligned}$$

and

$$\begin{aligned} s_n^3 = \tau _1 \frac{n^3}{m^{9/2}}+o\Big (\frac{n^3}{m^{9/2}}\Big ) = O\Big (\frac{n^3}{m^{9/2}}\Big ), \end{aligned}$$

where $\tau _0$ and $\tau _1$ are some constants and $m \rightarrow \infty$ with $n \rightarrow \infty$. Thus

$$\begin{aligned} \lim \limits _{n \rightarrow \infty } \frac{\sum _{i=1}^{n} {{E}}[|X_i - \mu _i|^3]}{s_n^3 } =\lim \limits _{n \rightarrow \infty } O\Big (\frac{1}{\sqrt{m}}\Big ) = 0. \end{aligned}$$

By the Lyapunov CLT, $\varvec{\epsilon }^T \varvec{U} \varvec{\epsilon }$ is asymptotically normally distributed. Therefore, $\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }/(2N)$ is asymptotically normally distributed. The mean of $\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }/(2N)$ can be shown to be

$$\begin{aligned} {{E}}\Big [\frac{\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }}{2N}\Big ] = \frac{1}{2N}{{E}}\Big [\sum _{i=1}^{n}\sum _{j=1}^{n} b_{ij} \epsilon _i\epsilon _j \Big ] = \frac{\sigma ^2}{2N}\textrm{tr}(\varvec{B}) = 0, \end{aligned}$$

and the variance is

$$\begin{aligned} \text {Var}\Big (\frac{\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }}{2N}\Big ) = {{E}}\Big [\Big (\frac{\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }}{2N}\Big )^2\Big ] = \frac{1}{4N^2}\Big [\sum _{i=1}^{n}b_{ii}^2 (E(\epsilon _i^4) - \sigma ^4)+2\sum _{i=1}^{n}\sum _{j=1,j\ne i}^{n} b_{ij}^2 \sigma ^4\Big ]. \end{aligned}$$

Using parts (a) and (b) of Lemma 3 and combining the above results, we have

$$\begin{aligned} \text {Var}\Big (\frac{\varvec{\epsilon }^T \varvec{B} \varvec{\epsilon }}{2N}\Big )&= \frac{1}{4N^2}\Big [\frac{15n^4}{14m}(E(\epsilon _i^4) - \sigma ^4) +\frac{45n^5}{m^3} \sigma ^4\Big ] + o\Big (\frac{n^2}{m^3}\Big )\\&= \frac{15}{56}(\gamma _4-1)\sigma ^4 \frac{n^2}{m^3} + o\Big (\frac{n^2}{m^3}\Big ), \end{aligned}$$

where $m = \lceil n^r\rceil$ with $2/3< r<1$. This then leads to

$$\begin{aligned} \sqrt{n^{3r-2}}(\hat{\beta }- \beta ) \xrightarrow []{D} N(0,\sigma _{b}^2), \end{aligned}$$

as $n \rightarrow \infty$, where $\sigma _{b}=\sqrt{15(\gamma _4-1)\sigma ^4/56}$. $\square$

Appendix 3: Proofs of Theorem 2 and Theorem 3

Proof of Theorem 2

The estimated error variance of $\hat{\beta }$ given in (9) can be written as $\tilde{\sigma }_{\beta }^2 = \tau _n \hat{\sigma }^4$. As $n \rightarrow \infty$, $\tau _n \rightarrow (15/28)n^{2-3r}$ with $m = \lceil n^r\rceil$ in (9). Let $\hat{\sigma }^2$ be a consistent estimator of $\sigma ^2$, and $\sigma _\beta ^2=(15/28)n^{2-3r}\sigma ^4$. Under Theorem 1 and the null hypothesis $H_0$ in (4), we have $\hat{\beta }/\sigma _{\beta } \xrightarrow []{D} N(0,1)$ when the random errors are normally distributed. In addition, we have $\sigma _{\beta }/\tilde{\sigma }_{\beta } \rightarrow 1$ as $n\rightarrow \infty$. Thus by Slutsky’s theorem,

$$\begin{aligned} T = \frac{\hat{\beta }}{\tilde{\sigma }_{\beta }} = \frac{\hat{\beta }}{\sigma _{\beta }}\cdot \frac{\sigma _{\beta }}{\tilde{\sigma }_{\beta }} \xrightarrow []{D} N(0,1) ~~~~\textrm{as}~ n \rightarrow \infty . \end{aligned}$$

$\square$

Proof of Theorem 3

Given that $\hat{\kappa }$ and $\hat{\sigma }^2$ are consistent estimators of $\kappa$ and $\sigma ^2$ respectively, we note that $\check{\sigma }_{\beta g}^2$ in (12) is also a consistent estimator of $\sigma _{\beta }^2= (15/56)n^{2-3r}(\kappa -(\sigma ^2)^2)$. Therefore under Theorem 1 and the null hypothesis $H_0$ in (4), by Slutsky’s theorem we have

$$\begin{aligned} G = \frac{\hat{\beta }}{\check{\sigma }_{\beta g}} = \frac{\hat{\beta }}{\sigma _{\beta }}\cdot \frac{\sigma _{\beta }}{\check{\sigma }_{\beta g}} \xrightarrow []{D} N(0,1) ~~~~\textrm{as}~ n \rightarrow \infty . \end{aligned}$$

$\square$