Topology optimization of load-bearing capacity

Abstract

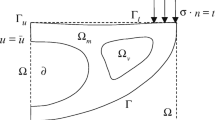
The present work addresses the problem of maximizing a structure load-bearing capacity subject to given material strength properties and a material volume constraint. This problem can be viewed as an extension to limit analysis problems which consist in finding the maximum load capacity for a fixed geometry. We show that it is also closely linked to the problem of minimizing the total volume under the constraint of carrying a fixed loading. Formulating these topology optimization problems using a continuous field representing a fictitious material density yields convex optimization problems which can be solved efficiently using state-of-the-art solvers used for limit analysis problems. We further analyze these problems by discussing the choice of the material strength criterion, especially when considering materials with asymmetric tensile/compressive strengths. In particular, we advocate the use of a L₁-Rankine criterion which tends to promote uniaxial stress fields as in truss-like structures. We show that the considered problem is equivalent to a constrained Michell truss problem. Finally, following the idea of the SIMP method, the obtained continuous topology is post-processed by an iterative procedure penalizing intermediate densities. Benchmark examples are first considered to illustrate the method overall efficiency while final examples focus more particularly on no-tension materials, illustrating how the method is able to reproduce known structural patterns of masonry-like structures. This paper is accompanied by a Python package based on the FEniCS finite-element software library.

Appendices

Appendix A: Proof that σ ∈ ρ G is a convex constraint

The constraint σ ∈ ρG is equivalent to σ/ρ ∈ G for ρ > 0. Let us consider any (σ₁, ρ₁) and (σ₂, ρ₂) such that ρ_i > 0 and σ_i/ρ_i ∈ G for i = 1, 2. Then, ∀λ ∈ [0; 1]:

$$ \begin{array}{@{}rcl@{}} \frac{(1-\lambda)\boldsymbol{\sigma}_{1} + \lambda \boldsymbol{\sigma}_{2}}{(1-\lambda)\rho_{1} + \lambda \rho_{2}} &=& \frac{(1-\lambda)\rho_{1}}{(1-\lambda)\rho_{1} + \lambda \rho_{2}}\frac{\boldsymbol{\sigma}_{1}}{\rho_{1}} + \frac{\lambda \rho_{2}}{(1-\lambda)\rho_{1} + \lambda \rho_{2}}\frac{\boldsymbol{\sigma}_{2}}{\rho_{2}} \\ &=& (1-\mu)\frac{\boldsymbol{\sigma}_{1}}{\rho_{1}} + \mu\frac{\boldsymbol{\sigma}_{2}}{\rho_{2}} \end{array} $$

(19)

where $\mu = \frac {\lambda \rho _{2}}{(1-\lambda )\rho _{1} + \lambda \rho _{2}}\in [0;1]$. Owing to the convexity of G, we obtain that $\frac {(1-\lambda )\boldsymbol {\sigma }_{1} + \lambda \boldsymbol {\sigma }_{2}}{(1-\lambda )\rho _{1} + \lambda \rho _{2}} \in G$ which proves that the set {(σ, ρ) s.t. σ ∈ ρG} is convex.

Appendix B: Proofs of solution properties of the relaxed problems

Property 1

: $\forall \eta ,\eta ^{\prime }\in [0;1]$ with $\eta \leq \eta ^{\prime }$ and $\eta ^{\prime }>0$:

$$ \frac{\eta}{\eta^{\prime}}\lambda^{+}(\eta^{\prime})\leq \lambda^{+}(\eta) \leq \lambda^{+}(\eta^{\prime}) $$

(20)

Proof

Let σ and ρ (resp. $\boldsymbol {\sigma }^{\prime }$ and $\rho ^{\prime }$) the solutions to (LOAD-MAX)(η) (resp. to (LOAD-MAX)($\eta ^{\prime }$)). Then, (λ⁺(η),σ, ρ) is feasible for problem (LOAD-MAX)($\eta ^{\prime }$) so that $\lambda ^{+}(\eta ) \leq \lambda (\eta ^{\prime })$. Besides, let us define $\widehat {\lambda }=\frac {\eta }{\eta ^{\prime }}\lambda ^{+}(\eta ^{\prime })$, $\widehat {\boldsymbol {\sigma }}=\frac {\eta }{\eta ^{\prime }}\boldsymbol {\sigma }^{\prime }$ and $\widehat {\rho }= \frac {\eta }{\eta ^{\prime }}\rho ^{\prime }$. Then, since $0\leq \frac {\eta }{\eta ^{\prime }} \leq 1$, we have $0\leq \widehat {\rho } \leq \rho ^{\prime } \leq 1$ and $\frac {1}{|\mathcal {D}|}{\int \limits }_{\mathcal {D}} \widehat {\rho }\text {dx} \leq \frac {\eta }{\eta ^{\prime }}\frac {1}{|\mathcal {D}|}{\int \limits }_{\mathcal {D}} \rho ^{\prime }\text {dx}=\eta$. Moreover, $(\widehat {\lambda },\widehat {\boldsymbol {\sigma }},\widehat {\rho })$ verify the equilibrium equations and we also have $\widehat {\boldsymbol {\sigma }} \in \widehat {\rho } G$. Thus, we have a feasible point for problem (LOAD-MAX)(η) and one therefore has $\widehat {\lambda }\leq \lambda ^{+}(\eta )$. □

Property 2

: $\forall \lambda ,\lambda ^{\prime }\in [0;{\varLambda }^{+}]$ and $\lambda \leq \lambda ^{\prime }$ and $\lambda ^{\prime }>0$:

$$ \eta^{-}(\lambda) \leq \frac{\lambda}{\lambda^{\prime}}\eta^{-}(\lambda^{\prime}) \leq \eta^{-}(\lambda^{\prime}) $$

(21)

Proof

The proof follows the same ideas as Property 1 when defining $(\boldsymbol {\sigma }^{\prime },\rho ^{\prime })$ solution to (VOL-MIN)($\lambda ^{\prime }$) and $\widehat {\boldsymbol {\sigma }}=\frac {\lambda }{\lambda ^{\prime }}\boldsymbol {\sigma }^{\prime }$ and $\widehat {\rho }= \frac {\lambda }{\lambda ^{\prime }}\rho ^{\prime }$. We then easily show that it is a feasible point for (VOL-MIN)(λ) associated with an objective value $\frac {1}{|\mathcal {D}|}{\int \limits }_{\mathcal {D}} \widehat {\rho } \text {dx} = \frac {\lambda }{\lambda ^{\prime }}\eta ^{-}(\lambda ^{\prime })$. □

Property 3

: λ⁺(η) and η⁻(λ) are non-decreasing functions. λ⁺(η) is continuous and η⁻(λ) is injective. Finally, we also have:

$$ \eta {\varLambda}^{+} \leq \lambda^{+}(\eta) \quad \forall \eta \in[0;1] $$

(22)

where Λ⁺ = λ⁺(1) is the ultimate load factor of the limit analysis problem.

Proof

The monotone property follows directly from Propositions 1 and 2. The continuity follows from Proposition 1 with $\lambda ^{\prime }=\lambda +\epsilon$ and 𝜖 → 0. Injectivity of η⁻(λ) follows from Proposition 2 when assuming that $\eta ^{-}(\lambda )=\eta ^{-}(\lambda ^{\prime })$ then $\lambda =\lambda ^{\prime }$. Finally, the inequality follows from the particular case $\eta ^{\prime }=1$ in Proposition 1. Indeed, for problem (LOAD-MAX), one can take ρ = 1 everywhere, yielding a classical limit analysis problem with an ultimate load factor Λ⁺ = λ⁺(1). □

Property 4

: We have:

$$ \begin{array}{@{}rcl@{}} \eta^{-}(\lambda^{+}(\eta)) &\leq \eta \quad \forall \eta \in[0;1] \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} \lambda^{+}(\eta^{-}(\lambda)) &\geq \lambda \quad \forall \lambda\in[0;{\varLambda}^{+}] \end{array} $$

(24)

Proof

Let (σ⁺, ρ⁺) (resp. (σ⁻, ρ⁻)) be a solution to (LOAD-MAX)(η) (resp. (VOL-MIN)(λ)). Then, (σ⁺, ρ⁺) is a feasible point for (VOL-MIN)(λ⁺(η)) associated with an objective value $\frac {1}{|\mathcal {D}|}{\int \limits }_{\mathcal {D}} \widehat {\rho } \text {dx} = \eta$. This proves the first inequality.

Similarly, (σ⁻, ρ⁻) is a feasible point for (LOAD-MAX) (η⁻(λ)) for a load factor λ. This proves the second inequality. □

Property 5

: For all λ ∈ [0; Λ⁺], λ⁺(η⁻(λ)) = λ, i.e., λ⁺ is the (left) inverse of η⁻ meaning that both problems (VOL-MIN) and (LOAD-MAX) are in fact equivalent.

Proof

Let us write the first inequality of Proposition 4 for η = η⁻(λ) for λ ∈ [0; Λ⁺], then:

$$ \eta^{-}(\lambda^{+}(\eta^{-}(\lambda))) \leq \eta^{-}(\lambda) $$

However, from the second inequality of Proposition 4, λ⁺(η⁻(λ)) ≥ λ. Using the fact that η⁻ is non-decreasing we also have that:

$$ \eta^{-}(\lambda) \leq \eta^{-}(\lambda^{+}(\eta^{-}(\lambda))) $$

Combining both results gives that η⁻(λ⁺(η⁻(λ))) = η⁻(λ), i.e., λ⁺(η⁻(λ)) = λ due to η⁻ being injective. □

Appendix C: Conic formulation for the L ₁-Rankine criterion in 2D

We consider the following isotropic criterion for 2D stress tensors σ:

$$ \boldsymbol{\sigma} \in G_{\text{L1-Rankine}} \Leftrightarrow g(\sigma_{I})+g(\sigma_{II}) \leq 1 $$

(25)

where σ_{I, II} are the principal stresses, $g(\sigma ) = \max \limits \left \lbrace \! \frac {\sigma }{f_{t}};\!-\frac {\sigma }{f_{c}}\!\right \rbrace$ and f_t, f_c the tensile and compressive strengths respectively.

In 2D, we explicitly have that:

$$ \begin{array}{@{}rcl@{}} \sigma_{I} &=& \frac{\sigma_{xx}+\sigma_{yy}}{2} + \frac{1}{2} \sqrt{(\sigma_{xx}-\sigma_{yy})^{2}+4\sigma_{xy}^{2}}\\ \sigma_{II} &=& \frac{\sigma_{xx}+\sigma_{yy}}{2} - \frac{1}{2} \sqrt{(\sigma_{xx}-\sigma_{yy})^{2}+4\sigma_{xy}^{2}} \end{array} $$

(26)

Introducing T = σ_xx + σ_yy and $R = \sqrt {(\sigma _{xx} - \sigma _{yy})^{2}+4\sigma _{xy}^{2}}$, we have that:

• If σ_I, σ_II > 0:

  $$ \sigma_{I} + \sigma_{II} \leq f_{t} \Leftrightarrow T \leq f_{t} $$

  (27)

• If σ_I, σ_II < 0:

  $$ -\sigma_{I} - \sigma_{II} \leq f_{c} \Leftrightarrow -T \leq f_{c} $$

  (28)

• If σ_I > 0 and σ_II < 0:

  $$ \begin{array}{@{}rcl@{}} \frac{\sigma_{I}}{f_{t}} - \frac{\sigma_{II}}{f_{c}} &\leq& 1 \Leftrightarrow T \left( \frac{1}{2f_{t}}-\frac{1}{2f_{c}}\right) + R\left( \frac{1}{2f_{t}}+\frac{1}{2f_{c}}\right) \!\leq\! 1 \\ &\Leftrightarrow& R \leq \left( \frac{2f_{t}f_{c}}{f_{c}+f_{t}}-T\frac{f_{c}-f_{t}}{f_{c}+f_{t}}\right) \end{array} $$

  (29)

Denoting by $\alpha = \frac {f_{c}-f_{t}}{f_{c}+f_{t}}$ and $\overline {f} =\frac {2f_{t}f_{c}}{f_{c}+f_{t}}$, we finally have the following conic formulation:

$$ \begin{array}{@{}rcl@{}} &&\boldsymbol{\sigma} \in G_{\text{L1-Rankine}} \Leftrightarrow - f_{c} \leq \sigma_{xx}+\sigma_{yy} \leq f_{t} \end{array} $$

(30)

$$ \begin{array}{@{}rcl@{}} && \begin{bmatrix} \alpha & \alpha & 0\\ 1 & -1 & 0\\ 0 & 0 & 2\\ \end{bmatrix} \begin{Bmatrix} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{xy} \end{Bmatrix} + \begin{Bmatrix} X_{0}\\ X_{1}\\ X_{2}\end{Bmatrix} = \begin{Bmatrix} \overline{f}\\ 0\\ 0 \end{Bmatrix} \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} && X_{0} \geq \sqrt{{X_{1}^{2}}+{X_{2}^{2}}} \end{array} $$

(32)

where the last condition is a quadratic conic constraint.

Finally, in the case of a density dependent criterion, we have:

$$ \begin{array}{@{}rcl@{}} &&\boldsymbol{\sigma} \in \rho G_{\text{L1-Rankine}}\Leftrightarrow \!-\rho f_{c} \leq \sigma_{xx}+\sigma_{yy} \leq \rho f_{t}the following conic formulation: \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} && \begin{bmatrix} \alpha & \alpha & 0\\ 1 & -1 & 0\\ 0 & 0 & 2\\ \end{bmatrix} \begin{Bmatrix} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{xy} \end{Bmatrix} + \begin{Bmatrix} X_{0}\\ X_{1}\\ X_{2}\end{Bmatrix}= \begin{Bmatrix} \rho\overline{f}\\ 0\\ 0 \end{Bmatrix} \end{array} $$

(34)

$$ \begin{array}{@{}rcl@{}} && X_{0} \geq \sqrt{{X_{1}^{2}}+{X_{2}^{2}}} \end{array} $$

(35)