Iteration-based adjoint method for the sensitivity analysis of static aeroelastic loads

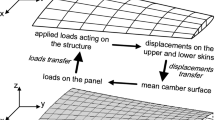
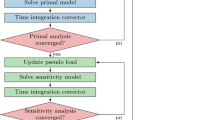
Abstract

The sensitivity analysis of static aeroelastic loads can be analytically performed by virtue of a modified stiffness matrix. However, introducing a modified stiffness matrix into the calculation will incur extra computational cost. Additionally, the intrinsic drawback of the direct method is disadvantageous for the sensitivity calculation with a large number of design variables. This paper therefore presents a novel iteration-based adjoint method for the sensitivity analysis of static aeroelastic loads acting on flexible wing, the basis of which is the static aeroelastic calculation via loosely coupled iteration between the potential-flow panel model and the structural linear finite element model. By using an iterative approach for evaluating the adjoint variable, modification to the original stiffness matrix can be obviated. Moreover, this method is more competent for the structural sensitivity analysis with a very large number of design variables, since the adjoint variable is unrelated to the designs. A rectangular wing and a swept wing are employed to demonstrate the verification of the algorithms. The design sensitivities of applied nodal forces on the structure, lift per unit span, total lift and root bending moment are calculated and analyzed. The computational cost is also discussed to further demonstrate the efficiency of the proposed method.

Appendix

Let Δu_s denote a perturbation in structural displacement vector, and Δf_s denote the change of structural load vector, we have

$$ \boldsymbol{K}\cdot\mathrm{\Delta}\boldsymbol{u}_{s}=\mathrm{\Delta}\boldsymbol{f}_{s} $$

(19)

The expression of Δf_s can be approximately written as

$$ \mathrm{\Delta}\boldsymbol{f}_{s}\approx \frac{\partial\boldsymbol{f}_{s}}{\partial\boldsymbol{u}_{s}}\cdot \mathrm{\Delta}\boldsymbol{u}_{s} $$

(20)

From (19) and (20), we obtain the following eigenvalue problem:

$$ \left[\lambda\cdot\boldsymbol{I}-\boldsymbol{K}^{-1}\cdot \frac{\partial\boldsymbol{f}_{s}}{\partial\boldsymbol{u}_{s}}\right]\cdot \mathrm{\Delta}\boldsymbol{u}_{s}= \boldsymbol{0} $$

(21)

This is the equation for divergence analysis, and the eigenvalue λ reflects the stability of static aeroelastic system. In particular, the largest positive eigenvalue represents the ratio of current flight dynamic pressure to critical divergence dynamic pressure (Rodden and Johnson 1994; Wright and Cooper 2015).

By using the symmetrical property of global stiffness matrix (Horn and Johnson 1985), the following relation can be obtained:

$$ \begin{array}{@{}rcl@{}} \det\left( \lambda\cdot\boldsymbol{I}-\boldsymbol{K}^{-1}\cdot \frac{\partial\boldsymbol{f}_{s}}{\partial\boldsymbol{u}_{s}}\right)&=& \det\left( \lambda\cdot\boldsymbol{I}-\frac{\partial\boldsymbol{f}_{s}}{\partial\boldsymbol{u}_{s}}\cdot \boldsymbol{K}^{-1}\right)\\ &=&\det\left( \lambda\cdot\boldsymbol{I}-\boldsymbol{K}^{-1}\cdot \left[\frac{\partial\boldsymbol{f}_{s}}{\partial\boldsymbol{u}_{s}}\right]^{T} \right) \end{array} $$

(22)

Therefore, the spectral radius (i.e., the largest absolute value of eigenvalue) of $\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}$ is equal to that of $\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T}$. The iteration of (11) and (16) will converge to the unique solution for any initial vector if and only if $\rho (\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s})$ and $\rho (\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T})$ are less than 1 (Stoer and Bulirsch 2002; Greenbaum and Chartier 2012). In engineering practice, the structure stiffness in a stable static aeroelastic system is usually large enough to make $\rho (\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s})<1$ and $\rho (\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T})<1$ be satisfied. This condition can also guarantee that the divergence (or structure failure) will not occur, and the equilibrium state of wing deformation will finally be achieved.

The values of $\rho (\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s})$ and $\rho (\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T})$ may reflect the convergence rates of (11) and (16), respectively. That is, the smaller the spectral radius, the faster the convergence rate will be (Stoer and Bulirsch 2002). Hence, the converged du_s/db_i and $\boldsymbol {J}_{\Phi }^{T}$ can be obtained with almost the same iteration steps.

∂f_s/∂u_s indicates the variation of aerodynamic forces in response to the displacement perturbations, and is unrelated to the structural property. So the structural stability is determinate for a wing with given stiffness, and then, $\rho (\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s})$ and $\rho (\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T})$ are also determinate. Therefore, different mesh divisions will affect the size of stiffness matrix, but have little influence on the iteration steps for convergence. In this research, unique FE mesh division is considered for both the rectangular and the swept wing models. Additionally, in these two numerical examples, the spectral radius of $\boldsymbol {K}^{-1}\cdot \partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}$ or $\boldsymbol {K}^{-1}\cdot \left [\partial \boldsymbol {f}_{s}/\partial \boldsymbol {u}_{s}\right ]^{T}$ is also the corresponding largest positive eigenvalue, namely, the ratio of current flight dynamic pressure to critical divergence dynamic pressure.