Interface crack between dissimilar thin-films with surface effect

Abstract

An interface crack between dissimilar elastic thin-films with surface effect has been investigated. By using integral transform technique the mixed boundary value problem of an interface crack is reduced to singular integral equations, which can be further reduced to a Riemann–Hilbert problem with analytical solution. The crack-tip singularities of the interface crack have been studied for possible combination of the dissimilar isotropic elastic materials with surface effect, and it is shown that there can be either oscillatory or non-oscillatory singularity for the interface crack. Analytical solution of the normal and shear stresses on the bonded interface is obtained, the relative crack opening displacement (COD) and relative crack sliding displacement (CSD) were given, and energy release rates (ERRs) for the interface crack are obtained for both oscillatory and non-oscillatory singularity cases. The oscillatory and non-oscillatory singularity parameters for interface cracks between dissimilar isotropic elastic materials with surface effect have been obtained.

Appendix A

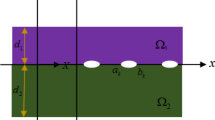
We consider dissimilar thin films of thickness h with an interface crack, see Fig.1, plane deformation is focused, and the displacement component along the thickness direction is neglected. The surface displacement components are taken as the bulk displacements at the same locations at the surface of the material.

If the body forces are neglected and the static problem is considered, the application of the principle of virtual work according to the bulk and surface stresses leads to

$$\begin{aligned} \int _S {\left( {\frac{h}{2}\sigma _{\alpha \beta } +\sigma _{\alpha \beta }^{S} +\sigma _{0} \delta _{\alpha \beta } } \right) \delta \varepsilon _{\alpha \beta } } dS-\frac{h}{2}\int _{\partial S} {f_{\alpha } \delta u_{\alpha } } d(\partial S)-\int _{\partial S} {\sigma _{0} n_{\alpha } \delta u_{\alpha } } d(\partial S)=0 \end{aligned}$$

(A.1)

where $\delta$ denotes the variation of a function, S is the area of the elastic plate and $\partial S$ is the boundary of S, $n_{\alpha }$ ($\alpha =1,2)$ is the unit outer normal vector to the boundary $\partial S$, and $f_{\alpha }$ are the density of surface forces independent of the thickness. It is noted that the second term and the third term on the left-hand side of Eq. (A.1) demonstrate the contribution of the surface forces and surface residual stress along the boundary $\partial S$, respectively.

Considering the following definition of strain with geometric nonlinearity terms

$$\begin{aligned} \varepsilon _{\alpha \beta } =\frac{1}{2}(u_{\alpha ,\beta } +u_{\beta ,\alpha } +u_{\gamma ,\alpha } u_{\gamma ,\beta } ) \end{aligned}$$

(A.2)

The substitution of Eq. (A.2) into Eq. (A.1) leads to

$$\begin{aligned} \int _S {\left[ {\left( {\frac{h}{2}\sigma _{\alpha \beta } +\sigma _{\alpha \beta }^{S} } \right) \delta \varepsilon _{\alpha \beta } +\sigma _{0} \delta _{\alpha \beta } u_{\gamma ,\beta } \delta u_{\gamma ,\alpha } } \right] } dS-\int _{\partial S} {\left[ {\frac{h}{2}f_{\alpha } +\sigma _{0} n_{\alpha } } \right] \delta u_{\alpha } } d(\partial S)=0 \end{aligned}$$

(A.3)

Applying the Green theorem to the first term of Eq. (A.3) leads to

$$\begin{aligned}&\int _S {\left[ {\left( {\frac{h}{2}\sigma _{\alpha \beta } +\sigma _{\alpha \beta }^{S} } \right) \delta \varepsilon _{\alpha \beta } +\sigma _{0} \delta _{\alpha \beta } u_{\gamma ,\beta } \delta u_{\gamma ,\alpha } } \right] } dS=\int _{\partial S} {\left( {\frac{h}{2}\sigma _{\alpha \beta } +\sigma _{\alpha \beta }^{S} +\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma } } \right) n_{\alpha } \delta u_{\beta } } d(\partial S) \nonumber \\&\quad -\int _S {\left( {\frac{h}{2}\sigma _{\alpha \beta ,\alpha } +\sigma _{\alpha \beta ,\alpha }^{S} +\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma \alpha } } \right) \delta u_{\beta } } dS \end{aligned}$$

(A.4)

and Eq. (A.3) can be rewritten as

$$\begin{aligned}&\int _{\partial S} {\left[ {\left( {\frac{h}{2}\sigma _{\alpha \beta } +\sigma _{\alpha \beta }^{S} +\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma } } \right) n_{\alpha } -\frac{h}{2}f_{\beta } -\sigma _{0} n_{\beta } } \right] \delta u_{\beta } } d(\partial S) \nonumber \\&\quad -\int _S {\left( {\frac{h}{2}\sigma _{\alpha \beta ,\alpha } +\sigma _{\alpha \beta ,\alpha }^{S} +\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma \alpha } } \right) \delta u_{\beta } } dS=0 \end{aligned}$$

(A.5)

By using the variational principle, the governing equation of elastic thin-films with surface elasticity effect can be obtained as

$$\begin{aligned} h\sigma _{\alpha \beta ,\alpha } +2\sigma _{\alpha \beta ,\alpha }^{S} +2\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma \alpha } =0 \end{aligned}$$

(A.6)

which is subjected to the following boundary condition

$$\begin{aligned} \left( {h\sigma _{\alpha \beta } +2\sigma _{\alpha \beta }^{S} +2\sigma _{0} \delta _{\alpha \gamma } u_{\beta ,\gamma } } \right) n_{\alpha } =hf_{\beta } +2\sigma _{0} n_{\beta } \end{aligned}$$

(A.7)

When the definition of the total incremental stress is introduced as in Eq. (5), the expansion of the governing equation (A.6) leads to Eqs. (3) and (4), and the boundary condition (A.7) leads to Eqs. (6) and (7).

The following identities for the integral of generalized functions have been used in the derivation of the singular integral equations (40)

$$\begin{aligned} \int _0^\infty {\cos (\xi x)\cos (\xi t)d\xi }= & {} \frac{\pi }{2}\delta (x-t) \nonumber \\ \int _0^\infty {\sin (\xi x)\sin (\xi t)d\xi }= & {} \frac{\pi }{2}\delta (x-t) \nonumber \\ \int _0^\infty {\frac{\sin (\xi x)\sin (\xi t)}{\xi }d\xi }= & {} \frac{1}{2}\log \left| {\frac{x+t}{x-t}} \right| \nonumber \\ \int _0^\infty {\cos (\xi x)\sin (\xi t)d\xi }= & {} \frac{t}{t^{2}-x^{2}} \end{aligned}$$

(A.8)

where $\delta ( )$ is the Dirac delta function.

In the derivation of the energy release rate (ERR) of the interface crack, the following integral identities have been used

$$\begin{aligned} \int _0^a {\sqrt{a^{2}-x^{2}} \cos \left( {\varepsilon \log \left| {\frac{a+x}{a-x}} \right| } \right) dx}= & {} \frac{\pi a^{2}\left( {1+4\varepsilon ^{2}} \right) }{4\cosh (\varepsilon \pi )} \end{aligned}$$

(A.9)

$$\begin{aligned} \int _0^a {\sqrt{a^{2}-x^{2}} \left[ {\left( {\frac{a+x}{a-x}} \right) ^{k}+\left( {\frac{a-x}{a+x}} \right) ^{k}} \right] dx}= & {} \frac{\pi a^{2}\left( {1-4k^{2}} \right) }{2\cosh (k\pi )} \end{aligned}$$

(A.10)

It is noted that Eqs. (A.9) and (A.10) are mathematically the same considering the integral identity that is shown in Eq. (93).