Multiple rigid line inclusions (anti-cracks) in a multilayered orthotropic medium under anti-plane loading

Abstract

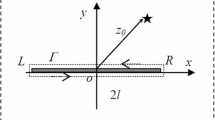
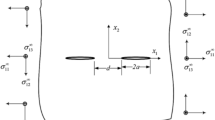
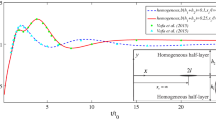
A non-homogeneous medium with multiple line inclusions is studied. The stiffness of the inclusions considered in this study is infinite. The model established can handle any non-homogeneity (continuous varying material properties or layered structures) and orthotropic in mechanical properties. The problem of rigid line inclusions in homogeneous medium can be considered as a special case of the model. Dependence of the inclusion tip fields on the strain intensity factor is given in closed form. Existence of multiple (parallel) inclusions can significantly reduce the strain intensity at the inclusion tips. However, the collinear inclusions will increase the strain intensity at the inclusion tips.

Appendices

Appendix A. Closed-form solution for a rigid line in an orthotropic material

The closed-form solutions for the rigid line inclusions in orthotropic media will be given. This can be done by solving the problem of an rigid line inclusion in an infinite orthotropic medium. The solution can be done by repeating the analysis of Section 2. Since the field quantities at infinity must be finite and the inclusion is at the middle of the medium, the displacements can be expressed as

$$\begin{aligned} w(x,y)=\gamma _{0} x+\frac{2}{\pi }\int \limits _0^\infty {e^{-s\lambda y}A(s)\sin (sx)\hbox {d}s} \end{aligned}$$

(A1)

where $\gamma _{0}$ is the share strain applied to the medium at infinity, A(s) is unknown and will be determined from the inclusion condition of the problem. In this Appendix, the notation $\lambda =\sqrt{G_{x} /G_{y} }$ is used.

The share stresses corresponding to Eq. (A1) are

$$\begin{aligned} \tau _{x}= & {} \tau _{0} +\frac{2G_{x} }{\pi }\int \limits _0^\infty {se^{-s\lambda y}A(s)\hbox {cos(}sx)\hbox {d}s} \end{aligned}$$

(A2)

$$\begin{aligned} \tau _{y}= & {} -\frac{2\lambda G_{y} }{\pi }\int \limits _0^\infty {se^{-s\lambda y}A(s)\sin \hbox {(}sx)\hbox {d}s} \end{aligned}$$

(A3)

in which $G_{x}$ and $G_{y}$ are the values of the shear modulus and $\tau _{0} =G_{x} \gamma _{0}$.

The jump of the shear stress $\tau _{y}$ across the inclusion plane g(x) is

$$\begin{aligned} g(x)=-\frac{2}{\pi G_{0} }\int \limits _0^\infty {sA(s)\sin \hbox {(}sx)\hbox {d}s} . \end{aligned}$$

(A4)

where $G_{0} =-\frac{1}{2\lambda G_{y} }$ is a constant depending on the elasticity properties of the material.

The inversion of Eq. (A4) gives

$$\begin{aligned} A(s)=G_{0} \int \limits _0^a {\frac{g(r)}{s}\sin (sr)\hbox {d}r} . \end{aligned}$$

(A5)

With the substitution of Eq. (A5), the share strain $\gamma _{x}$ at the inclusion plane can be obtained from Eq. (A1). This yields

$$\begin{aligned} \gamma _{x} =\gamma _{0} +\frac{2}{\pi }G_{0} \int \limits _0^\infty {\int \limits _0^a {g(r)\sin (sr)\cos (sx)\hbox {d}r} \hbox {d}s} \end{aligned}$$

(A6)

Since the strain $\gamma _{x}$ inside the inclusion is zero, Eq. (A6) will result in a singular integral equation. The solution is

$$\begin{aligned} g(r)=-\frac{\gamma _{0} }{G_{0} }\frac{r}{\sqrt{a^{2}-r^{2}} } \end{aligned}$$

(A7)

Note that Eq. (A6) is valid inside the inclusion as well as outside of the inclusion. In the case of outside of the inclusion, the strain in the inclusion line can be obtained with the substitution of Eq. (A7) and using Eq. (17). This yields

$$\begin{aligned} \gamma _{x} (x)=\gamma _{0} \frac{\left| x \right| }{\sqrt{x^{2}-a^{2}} },\quad \left| x \right| >a . \end{aligned}$$

(A8)

As expected, the strain is equal to $\varepsilon _{0}$ at infinity. However, when x approaches the inclusion tip a, the strain is singular. The strain intensity factor $K_{{0}}$ can be defined as

$$\begin{aligned} K_{{0}} =\lim \limits _{x\rightarrow a+0} \sqrt{2\pi (x-a)} \gamma (x). \end{aligned}$$

(A9)

With the substitution of Eq. (A8), Eq. (A9) gives

$$\begin{aligned} K_{{0}} =\gamma _{0} \sqrt{\pi a} . \end{aligned}$$

(A10)

Thus, the strain intensity factor for an infinite medium does not depend on the material properties.

The full field can be obtained with the substitution ofg into Eq. (A5):

$$\begin{aligned} A(s)=-\frac{\gamma _{0} }{s}\int \limits _0^a {\frac{r}{\sqrt{a^{2}-r^{2}} }\sin (sr)\hbox {d}r} . \end{aligned}$$

(A11)

Based on the well-known integral (B3) of Appendix B, A is obtained as

$$\begin{aligned} A(s)=-\frac{\pi a}{2s}\gamma _{0} J_{1} (sa) \end{aligned}$$

(A12)

The stresses can be obtained from Eqs. (A2) and (A3) with the substitution of Eq. (A12) and using the well-known integrals

$$\begin{aligned}&\int \limits _0^\infty {\hbox {exp}(-s\lambda y)J_{1} (as)\cos (xs)\hbox {d}s} =\frac{1}{a}-\frac{x}{a}\frac{1-\left( {\frac{a^{2}-L^{2}}{L_{1} L_{2} }} \right) }{\sqrt{x^{2}-L^{2}} }, \end{aligned}$$

(A13)

$$\begin{aligned}&\int \limits _0^\infty {\hbox {exp}(-s\lambda y)J_{1} (as)\sin (xs)\hbox {d}s} =\frac{\lambda y}{a}\frac{1}{\sqrt{x^{2}-L^{2}} }\frac{L^{2}}{L_{1} L_{2} }, \end{aligned}$$

(A14)

where

$$\begin{aligned} L_{1}= & {} \sqrt{(a+x)^{2}+(\lambda y)^{2}} \end{aligned}$$

(A15)

$$\begin{aligned} L_{2}= & {} \sqrt{(a-x)^{2}+(\lambda y)^{2}} \end{aligned}$$

(A16)

$$\begin{aligned} L= & {} \frac{L_{1} -L_{2} }{2} \end{aligned}$$

(A17)

The results are

$$\begin{aligned} \tau _{x}= & {} \tau _{0} -G_{x} \gamma _{0} \left( {1-x\frac{1-\left( {\frac{a^{2}-L^{2}}{L_{1} L_{2} }} \right) }{\sqrt{x^{2}-L^{2}} }} \right) \end{aligned}$$

(A18)

$$\begin{aligned} \tau _{y}= & {} G_{y} \gamma _{0} \frac{\lambda y}{\sqrt{x^{2}-L^{2}} }\frac{L^{2}}{L_{1} L_{2} } \end{aligned}$$

(A19)

They can be expressed in terms of the strain intensity factor $K_{{0}}$ as

$$\begin{aligned} \tau _{x}= & {} \tau _{0} -\frac{G_{x} K_{0} }{\sqrt{\pi a} }\left( {1-x\frac{1-\left( {\frac{a^{2}-L^{2}}{L_{1} L_{2} }} \right) }{\sqrt{x^{2}-L^{2}} }} \right) \end{aligned}$$

(A20)

$$\begin{aligned} \tau _{y}= & {} \frac{G_{y} K_{0} }{\sqrt{\pi a} }\frac{\lambda y}{\sqrt{x^{2}-L^{2}} }\frac{L^{2}}{L_{1} L_{2} } \end{aligned}$$

(A21)

Equations (A18)–(A21) are the closed-form solution of the stress field for a rigid line inclusion in an orthotropic medium under remote applied strain load. If the applied is the remote stress load $\tau _{x} =\tau _{0}$, the equivalent applied strain will be $\gamma _{0} =\tau _{0} /G_{x}$.

The above results of Eqs. (A20) and (A21) are for the stress distribution. In the special case of isotropic materials, they are same as the closed-form solution at the inclusion tips in [12]. Note that the current model is more general than Ref. [12] as it can deal with orthotropic materials.

Overall, the stresses have maximum values on the inclusion plane, $y =$ 0. These are

$$\begin{aligned} \tau _{x}= & {} 0,\quad x<a \end{aligned}$$

(A22)

$$\begin{aligned} \tau _{y}= & {} \frac{G_{y} \gamma _{0} x}{\sqrt{a^{2}-x^{2}} }=\frac{G_{y} K_{0} x}{\sqrt{\pi a} \sqrt{a^{2}-x^{2}} },\quad x<a \end{aligned}$$

(A23)

$$\begin{aligned} \tau _{x}= & {} \frac{G_{x} \gamma _{0} x}{\sqrt{x^{2}-a^{2}} }=\frac{G_{x} K_{0} x}{\sqrt{\pi a} \sqrt{x^{2}-a^{2}} },\quad x>a \end{aligned}$$

(A24)

$$\begin{aligned} \tau _{y}= & {} 0,\quad x>a \end{aligned}$$

(A25)

Therefore, the shear stress $\tau _{x}$ vanishes inside the inclusion region but singular immediately outside of the inclusion tip. In contrast, the shear stress $\tau _{y}$ is singular immediately inside of the inclusion tip but zero outside of the inclusion region.

The stress intensity factors are defined according to

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {K_{x} } \\ {K_{y} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\lim \limits _{x\rightarrow a+0} \sqrt{2\pi (x-a)} \tau _{x} (x)} \\ {\lim \limits _{x\rightarrow a-0} \sqrt{2\pi (a-x)} \tau _{y} (x)} \\ \end{array} }} \right\} . \end{aligned}$$

(A26)

and are obtained from Eqs. (A23) and (A22) as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {K_{x} } \\ {K_{y} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {G_{x} K_{0} } \\ {G_{y} K_{0} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {G_{x} \gamma _{0} \sqrt{\pi a} } \\ {G_{y} \gamma _{0} \sqrt{\pi a} } \\ \end{array} }} \right\} \end{aligned}$$

(A27)

Appendix B

$$\begin{aligned}&\int \limits _0^1 {\frac{T_{n} ({{\overline{r}}} )\sin (s{{\overline{r}}} )}{\sqrt{1-{{\overline{r}}}^{2}} }} \hbox {d}{{\overline{r}}} =\frac{\pi }{2}(-1)^{[(n-1)/2]}J_{n} (s),n=1,3,5\ldots , \end{aligned}$$

(B1)

$$\begin{aligned}&\int \limits _0^1 {\frac{T_{n} ({{\overline{r}}} )\cos (s{{\overline{r}}} )}{\sqrt{1-{{\overline{r}}}^{2}} }} \hbox {d}{{\overline{r}}} =\frac{\pi }{2}(-1)^{n/2}J_{n} (s),n=0,2,4,\ldots , \end{aligned}$$

(B2)

The above equations are equivalent to

$$\begin{aligned}&\int \limits _0^a {\frac{T_{n} (r/a)\sin (sr)}{\sqrt{a^{2}-r^{2}} }} \hbox {d}r=\frac{\pi }{2}(-1)^{[(n-1)/2]}J_{n} (sa),n=1,3,5\ldots , \end{aligned}$$

(B3)

$$\begin{aligned}&\int \limits _0^a {\frac{T_{n} (r/a)\cos (sr)}{\sqrt{a^{2}-r^{2}} }} \hbox {d}r=\frac{\pi }{2}(-1)^{n/2}J_{n} (sa),n=0,2,4\ldots , \end{aligned}$$

(B4)