A fully nonlinear Feynman–Kac formula with derivatives of arbitrary orders

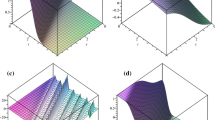
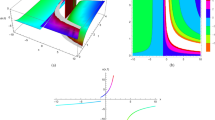
Abstract

We present an algorithm for the numerical solution of nonlinear parabolic partial differential equations. This algorithm extends the classical Feynman–Kac formula to fully nonlinear partial differential equations, by using random trees that carry information on nonlinearities on their branches. It applies to functional, non-polynomial nonlinearities that are not treated by standard branching arguments, and deals with derivative terms of arbitrary orders. A Monte Carlo numerical implementation is provided.

A Computer codes

The following codes implement the algorithm of Theorem 1 in Mathematica using an exponential distribution $\rho (t) = \textrm{e}^{-t}$, $t\ge 0$. In the above examples the values of fdb[n,k] have been precomputed by memoization for k up to 7 in order to speed up the solution algorithm, where n denotes the highest order of derivative $\partial _x^n$ in (1.1). The next code implements the mechanism $c \mapsto {\mathcal {M}}(c)$ in the procedure “codetofunction” via the combinatorics of the Faà di Bruno formula written the function “fdb”.

Numerical solution estimates are then computed using the following program, in which the code $\partial _x^k$ is represented by $\{-k\}$, $k\ge 1$, and the code $\big ( \partial _{z_0}^{\lambda _0} \cdots \partial _{z_n}^{\lambda _n} f\big )^*$ is represented by $\{ \lambda _0, \ldots , \lambda _n \} \in {\mathord {{\mathbb {R}}}}^{n+1}$.