Bayesian Inversion of MDJ Seismograms for Source Parameters and Yields of DPRK Underground Nuclear Explosions 2 to 6

Abstract

The Democratic People’s Republic of Korea (DPRK) conducted six underground nuclear explosions at the Punggye-ri nuclear test site at Mount Mantap, a granite peak. Test 1 was separate from tests 2 to 6, which were within about 1 km of each other. Using seismograms recorded at Mudanjiang (MDJ) seismic station in China, I propose a new approach to obtain source parameters, source time functions and yields of events 2 to 6, assuming they share the same Green’s function from Punggye-ri to MDJ. Each source is modelled as a spherical cavity in a homogeneous isotropic elastic full space, with four independent parameters constrained by published data on the properties of granite and analysis of the recorded MDJ seismograms. The effect of the ground surface is included as a planar reflection that modifies the pressure at the cavity boundary. The Green’s function for each event is estimated by deconvolving the seismogram for the estimated source time function. Very fast simulated annealing (VFSA) is used to search the parameter space to minimise the root-mean square difference among the estimated Green’s functions and their mean. The estimated Green’s functions are similar and differ in amplitude by less than a factor of 2. Green’s functions from Punggye-ri to other seismic stations may be obtained by deconvolving the seismograms for the corresponding source time functions. Map** the nonlinear zones surrounding each explosion indicates that this part of the site was destroyed by the underground nuclear tests before its official destruction on 24 May 2018.

1 Introduction

1.1 DPRK Nuclear Tests

The Democratic People’s Republic of Korea (DPRK) has conducted six underground nuclear tests at the Punggye-ri test site, as detailed in Table 1. The events were readily detected on seismometers and identified as explosions, beginning with the first, smallest event (e.g. Richards & Kim, 2007). Voytan et al. (2019) reported that, “Precise relative locations for the six explosions, with uncertainties on the order of a few hundred metres, have been determined by numerous seismic differential arrival time studies (e.g., Carluccio et al., 2014; Gibbons et al., 2017, 2018; He et al., 2018; Murphy et al., 2013; Myers et al., 2018; Selby, 2010; Wang et al., 2018; Wen & Long, 2010; Yao et al., 2018; Zhang & Wen, 2013; Zhao et al., 2016, 2017)”. Figure 1 shows the estimated locations of all six events at Mount Mantap according to Myers et al. (2018). The pattern is largely in agreement with other studies. For this paper the significant feature of the location pattern is the close proximity of tests 2 to 6, which are all within about 1 km of each other. The principal goal in this paper is to determine the source time functions of tests 2 to 6 using seismograms from the seismic station Mudanjiang (MDJ) in China.

Table 1 Dates of DPRK underground nuclear tests

Figure 1

a Event epicentres and 0.95 probability ellipses, labelled in order of occurrence. b Google Earth perspective of event epicentres. (Myers et al., 2018)

Figure 2 shows the MDJ seismograms for the five tests, 2 to 6 with individual amplitude scaling. Figure 3 shows the same seismograms all with the same amplitude scale, from which it is obvious that there is a huge variation in the size of these explosions, with No. 6 clearly much larger than all the others. The yields of these events are clearly of interest and have been the subject of much study. Before coming to the main point of this paper, it is worth discussing the problem of yield estimation, because it faces some of the same difficulties that confront the determination of source parameters.

Figure 2

MDJ seismograms for DPRK underground nuclear tests 2 to 6: individual amplitude scaling

Figure 3

MDJ seismograms for DPRK underground nuclear tests 2 to 6: same amplitude scaling

1.2 Estimation of Yields

The yield of an explosion is the quantity of energy it generates. The concept is easy to understand, but to measure it using seismic data is fraught with difficulty. Rodean (1971) summarised the state of unclassified knowledge of the coupling between underground nuclear explosions and seismic signals. Immediately after detonation, the temperature of the weapon is several tens of millions of degrees Kelvin and the pressures are estimated to be many millions of atmospheres. The rock adjacent to the explosion is vaporised; beyond that it is melted, although some rocks sublime (Rodean, 1971); beyond that it is fractured. The expanding gases compress the rock in the radial direction, creating tension tangentially. Since the solid rock is strong in compression, but weak in tension, the expansion causes radial fractures into which the gases expand. At a certain radius, known as the elastic radius, the tensile strength of the rock is sufficient to prevent further fracturing. Beyond this radius, the propagation is elastic.

The percentage of total explosive energy that is converted to seismic waves is small. Rodean (1971) quotes several estimates that vary by orders of magnitude, even for the same explosion. The range is approximately 0.1% to 5%. That is, at least 95% of the energy is contained within the elastic radius, perhaps as much as 99.9%. Yield estimates are made from the small fraction of energy in the seismic waves. Rodean does not define yield.

In their classic book Monitoring Underground Nuclear Explosions Dahlman and Israelsson (1977) devote a chapter to yield estimation. Yields are usually given in kilotons (kt), where 1 kt is equal to 4.2 × 10¹² J, or the energy released by exploding 1000 tons of trinitrotoluene (TNT). Yield estimates are made from seismograms. To estimate the yield, it is necessary to take account of the way the Earth affects the signal on its path from the source to the seismometer. Dahlman and Israelsson provide several formulas relating yield to magnitude, quoting several authors. The formulas are mostly of the form

$$ \log_{10} (A/T) = B\log_{10} (Y) + C, $$

(1)

where A is the peak amplitude of the P wave, T is the dominant period of the P wave, Y is the yield and B and C are constants that depend on the site of the source (for example Nevada Test Site, NTS), the rock the source was in, and attenuation along the path between the source and the seismometer. The term on the left-hand side is body wave magnitude m_b. Dalman and Israelsson doubt whether the formulas that work for NTS will work for other test sites. Each case needs to be calibrated. Table 2 from Voytan et al. (2019) summarises published yield estimates of the six DPRK underground nuclear tests, in which the ratio of largest to smallest estimate of yield for a given event can be as much as 10. Using preferred yield estimates from intercorrelation, W_IC, Voytan et al. (2019) determined the following yield-calibrated relation for the Punggye-ri test site.

$$ m_{bNEIC} = 0.9\log_{10} (W_{IC} ) + 4.13, $$

(2)

where m_bNEIC is the body-wave magnitude from the USGS National Earthquake Information Center.

Table 2 Summary ranges for published estimates of yield and depth of burial of DPRK underground nuclear tests from various studies (from Voytan et al., 2019)

1.3 Determination of Source Parameters

The problem of determination of source parameters of underground nuclear explosions from seismic data is not new and is of course related to yield estimation. Filson and Frasier (1972) identified the problem. They analysed data from five presumed explosions in eastern Kazakh measured at five teleseismic arrays: the Large Aperture Seismic Array (LASA) in Montana, USA, The Yellowknife Seismological Array (YKA), Northwest Territories, Canada, the Lillehammer Array (OONW), Norway, the Warramunga Array (WRA), Australia, and the Gauribidanur Array (GBA), India. They were aware of several analytic models for the buried explosive source (Blake, 1952; Haskell, 1967; Sharpe, 1942). In one approach to their analysis, they attempted to fit the displacement spectra of each event recorded at all five arrays to the parameters of Haskell’s source model. They stated the problem as follows: “This analysis was complicated by the fact that transmission effects, including attenuation, had to be estimated along with the parameters of the source functions, since the arrays are at different azimuths and distances from the eastern Kazakh test site” (p. 2046). This is basically the same problem that confronts yield estimation.

A seismogram is the convolution of the source time function with the earth impulse response, or Green’s function, plus noise. Given the proximity of DPRK tests 2 to 6, I assume the impulse response is essentially the same for all five seismograms recorded by MDJ. Filson and Frasier (1972) may have been the first to eliminate common-path effects in the estimation of explosive source parameters, by finding ratio filters between presumed explosion events in eastern Kazakh recorded at the same teleseismic array. I also intend to eliminate the path effects and introduce a different approach. Deconvolution of any of the five MDJ seismograms, 2 to 6, for the corresponding source time function should yield the impulse response, or Green’s function. The source time functions are not known, of course, but they can be modelled. The goals of this paper are (1) to estimate the source model parameters and source time functions of tests 2 to 6, (2) to estimate their yields. and (3) to estimate the Green’s function from Punggye-ri to MDJ.

The theory can be tested using another seismometer that records at least two of the five tests: deconvolution of the seismograms for the corresponding source time functions yields estimated Green’s functions that should be essentially the same.

The method I use is based on an idea I presented recently for the determination of explosive source time functions in seismic exploration, in which two unequal explosive charges in the same shot hole were assumed to have the same impulse response to a given receiver (Ziolkowski, 2022). The source time functions were modelled using Blake’s (1952) explosion model and the seismograms were deconvolved for the modelled source time functions to obtain estimated Green’s functions. The source parameters were adjusted to minimise the difference between the estimated Green’s functions. These seismic exploration explosions were from charges of the order of 1 kg. According to yield estimates discussed above, DPRK underground nuclear tests were 6 to 8 orders of magnitude bigger. I assume the same basic theory applies.

Blake’s (1952) source model is a spherical cavity, with internal pressure P(t), in an isotropic elastic whole space. Prior to Blake, Jeffreys (1931) and Sharpe (1942) had produced similar models but both assumed the Lamé constants $\lambda$ and $\mu$ to be equal. Blake allowed them to be unequal. Since Blake, there have been many papers on this topic using the same basic model, including Haskell (1967) and Mueller and Murphy (1971). Denny and Johnson (1991) provide a fine review of the subject and an extensive list of references. Voytan et al. (2019) use the source model of Mueller and Murphy (1971) for their analysis of the DPRK events. It is interesting that Mueller and Murphy (1971) were unaware of Blake’s (1952) work. In this paper the model is based on Blake’s formulation and further includes the reflection from the free surface.

An estimate of the Green’s function from Punggye-ri to MDJ is obtained for each source by deconvolving the corresponding seismogram for the modelled source time function. A Bayesian approach is used to look for a solution. The reciprocal of the square-root of the sum of the squares of the differences between the individual recovered Green’s functions and the mean Green’s function is defined as the likelihood function. The estimated posterior probability density function is the likelihood function multiplied by the prior estimate of the probability of the model. Very fast simulated annealing (VFSA) (Ingber, 1989, 1993; Sen & Stoffa, 2013) is used to search the model space for the optimum model.

1.4 Destruction of the Punggye-ri Test Site

On 24 May 2018, the test site was “destroyed” using explosive demolition packs of roughly 5 kg (Pabian et al., 2018). Figure 4, given to journalists invited to witness the destruction, shows a non-engineering map of the layout of the tunnels at Punggye-ri and the locations of the six underground nuclear tests, numbered sequentially. It corroborates the approximate geometry determined by Myers et al. (2018). This map is important for specification of the source model parameters. First, it shows the relative lateral locations of the explosions. That is, the locations provided by this map are preferred to the locations determined by seismic methods in conjunction with other observations. Second, it shows contours of the surface topography at 10 m intervals. Allowing a gentle gradient of 4% for drainage, as discussed by Voytan et al. (2019), the elevation of each of sources 2 to 6 can be estimated relative to tunnel portal Number 2. Source depth can then be estimated from the contours.

Figure 4

Layout of DPRK underground nuclear tests, showing four numbered portals in yellow, tunnels in red and blue, locations of numbered nuclear tests with red flags, explosions for destruction of the site with stars, and 1 km grid squares. Contours of the surface topography at 10 m intervals are hard to see at this scale

“Destroyed” is put in quotation marks above because Pabian et al. (2018) state it would be possible to reopen the site. Specifically, they state, “Analysis of ground photos and video taken at North Korea's Punggye-ri Nuclear Test Site (courtesy of Sky News) from the recent site closing event can confirm only that the test tunnel entrances were sealed. At most, two other point detonations were carried out (as was claimed) in each of the three tunnels, while the tunnel branches probably remain intact. While the procedures carried out by the North Koreans will make reusing the site difficult in the future, regaining access to the completed test tunnels at the South and West Portals may still be possible. However, enough demolition has been done that, if North Korea chose to reopen the test site, major excavation as well as construction of at least some support structures would be needed, and such activity would almost certainly be detectable via satellite imagery.” To put the “destruction” in context, it is worth noting that “destruction” consisted of about 10 explosions each of a few kg of explosive. We should compare these explosions with the six underground nuclear explosions that had already taken place, each of which was 6 to 8 orders of magnitude bigger.

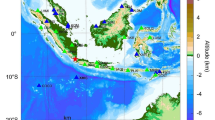
In this paper I describe the explosion source model and its parameterisation, the deconvolution operation, model optimisation and VFSA. The process leads to an estimated source time function and yield for each of the DPRK explosions 2 to 6 and an estimate of the Green’s function from Punggye-ri to MDJ. The theory is tested using seismograms recorded at Incheon seismic station (INCN), South Korea, and Baijiatuan, seismic station (BJT), Bei**g, China. The map in Fig. 5 shows the positions of the three seismic stations in relation to the Punggye-ri test site.

Figure 5

Map showing Punggye-ri test site (red filled circle) in relation to seismic stations MDJ, INCN and BJT (black filled circles)

2 Method

2.1 An Underground Nuclear Explosion

Modelling of nuclear explosions is very advanced, beginning with the Lagrangian finite-element numerical scheme of Cherry and Hurdlow (1966), and continuing to the present day with the sophisticated modelling of Myers et al. (2018). For our purposes, we are looking for a model that contains the main elements of the explosion, with as few parameters as possible.

2.2 Blake’s Explosion Source Model

Figure 6 shows the model for Blake’s (1952) spherical explosive source, of radius $a$, embedded in a homogeneous isotropic full space. The pressure on the inside of the sphere is $P(t)$, where $t$ is time. Blake (1952) solved the problem for a step in pressure $P(t) = p_{0} H(t)$, with $p_{0}$ a constant and $H(t)$ the Heaviside unit step function. Any arbitrary pressure function can then be incorporated in the solution using Duhamel’s integral.

Figure 6

Blake’s (1952) model, in which an internal pressure $P(t)$ is applied uniformly over the interior surface of a cavity of radius $a$, buried in an infinite homogeneous isotropic elastic medium with density $\rho$ and Lamé elastic constants $\lambda$ and $\mu$

The origin is at the centre of the sphere and the motion is radial. The displacement $u(r,t)$ is a function of radial distance $r$ and time $t$ and is the gradient of a displacement potential $\phi (r,t)$, which is a solution of the scalar wave equation

$$ \nabla^{2} \phi = \frac{1}{{c^{2} }}\frac{{\partial^{2} \phi }}{{\partial t^{2} }}. $$

(3)

For an outgoing spherical wave,

$$ \phi = \frac{1}{r}f(\tau ),\,\,r \ge a, $$

(4)

where

$$ \tau = t - (r - a)/c, $$

(5)

$$ c = \left( {\frac{\lambda + 2\mu }{\rho }} \right)^{\frac{1}{2}} . $$

(6)

Rather than use $\lambda$ and $\mu$ as the elastic constants, Blake used P-wave velocity $c$ and Poisson’s ratio $\sigma = \lambda /2(\lambda + \mu )$, which are more convenient. The displacement may be written as

$$ u = \frac{\partial \phi }{{\partial r}} = - \left[ {\frac{1}{{r^{2} }}f(\tau ) + \frac{1}{rc}f^{\prime } (\tau )} \right], $$

(7)

where the prime denotes differentiation with respect to the argument. Equation 7 may be written as

$$ u(r,t) = - f(t)*\left[ {\frac{1}{{r^{2} }}\delta \left( {t - \frac{r - a}{c}} \right) + \frac{1}{rc}\delta^{\prime } \left( {t - \frac{r - a}{c}} \right)} \right], $$

(8)

where the asterisk denotes convolution and the term in square brackets is the Green’s function for a whole space, with $\delta (t)$ the Dirac impulse function. The first $(1/r^{2} )$ term in the Green’s function dominates at distances small compared with a wavelength; this is known as the near field. The second $(1/r)$ term dominates at distances large compared with a wavelength; this is known as the far field. The convolution occurs right at the source: $r = a$. The propagating seismic wavelet is the sum of the near-field term and the far-field term and changes shape as it propagates. Its shape is constant only in the far field, at distances large compared with a wavelength.

The function $\left[ { - f(t)} \right]$ is the reduced displacement potential [RDP] and is ‘reduced’ because it is independent of distance $r$ (Werth et al., 1962). $\left[ { - f(t)} \right]$ has dimensions of volume. We measure ground velocity or acceleration, not displacement. The time derivative of Eq. 6 yields the ground velocity

$$ v(r,t) = \frac{\partial u(r,t)}{{\partial t}} = - f^{\prime } (t)*\left[ {\frac{1}{{r^{2} }}\delta \left( {t - \frac{r - a}{c}} \right) + \frac{1}{rc}\delta^{\prime } \left( {t - \frac{r - a}{c}} \right)} \right], $$

(9)

in which $\left[ { - f^{\prime } (t)} \right]$ is the reduced velocity potential (RVP) and is the source time function for velocity seismograms. $\left[ { - f^{\prime}(t)} \right]$ has dimensions of volume divided by time. In the near field the wavelet has almost the same shape as the source time function; in the far field the wavelet has the shape of the time-derivative of the source time function.

The Green’s function for an explosive source in a whole space has only the two terms in the square brackets in Eqs. 8 and 9. In general, the Green’s function is more complicated than this. The boundary condition is continuity of pressure at the elastic radius $r = a$. We normally assume that the source time function is unaffected by scattering from changes in medium properties and the response at a receiver is the convolution of the source time function with the Green’s function. In practice, it is possible to include the reflection from the surface, which is important where the source is shallow, which is the case for underground nuclear explosions.

Blake derived the following expression for the displacement potential:

$$ \phi (r,\tau ) = \frac{{p_{0} a^{3} K}}{{\rho c^{2} r}}\left[ { - 1 + \left( {\frac{4K}{{4K - 1}}} \right)^{\frac{1}{2}} \exp ( - \alpha_{0} \tau )\cos \left( {\omega_{0} \tau - \tan^{ - 1} \left( {\frac{1}{4K - 1}} \right)^{\frac{1}{2}} } \right)} \right], $$

(10)

where:

$$ K = (1/2)(1 - \sigma )/(1 - 2\sigma ); $$

(11)

$$ \alpha_{0} = c/2aK; $$

(12)

$$ \omega_{0} = \alpha_{0} (4K - 1)^{\frac{1}{2}} . $$

(13)

For velocity seismograms the source time function is the reduced velocity potential (RVP) with SI units of m³ s⁻¹:

$$ \begin{gathered} s(\tau ) = - \frac{{\partial \left( {r\phi (r,\tau )} \right)}}{\partial \tau } = \frac{{p_{0} a^{3} K}}{{\rho c^{2} }}\left( {\frac{4K}{{4K - 1}}} \right)^{\frac{1}{2}} \exp ( - \alpha_{0} \tau ) \hfill \\ \times \,\left[ {\alpha_{0} \cos \left( {\omega_{0} \tau - \tan^{ - 1} \left( {\frac{1}{4K - 1}} \right)^{\frac{1}{2}} } \right) + \omega_{0} \sin \left( {\omega_{0} \tau - \tan^{ - 1} \left( {\frac{1}{4K - 1}} \right)^{\frac{1}{2}} } \right)} \right],\,\tau \ge 0. \hfill \\ \end{gathered} $$

(14)

The Fourier transform of this function is obtainable from Blake’s Appendix V (Ziolkowski, 2021), and is

$$ S(\omega ) = \frac{{p_{0} a}}{\rho }\frac{1}{{\left[ {\omega - \omega_{0} - i\alpha_{0} } \right]\left[ {\omega + \omega_{0} - i\alpha_{0} } \right]}}. $$

(15)

2.3 Inclusion of the Free Surface Reflection

A detailed analysis of the free surface reflection is included in the paper by Gaebler et al. (2019), who show pP and reflected SV energy simulated in a 2D model. Their analysis includes an estimate of yield. They recognize the need to start with a reliable estimate of body-wave magnitude m_b and, since no magnitude-yield relation has been “approved” for the DPRK test site, they apply the magnitude-yield relation proposed by Bowers et al. (2001), developed for the Novaya Zemlya region to find a magnitude of 400 kt. This is 33% larger than the largest estimate in Table 2. The interaction of the reflection from the surface with the source is not considered.

In this paper the reflection from the free surface is included in the modelling by considering it as a wave of opposite polarity originating from a virtual source above the surface, as shown in Fig. 7. The effect of the reflection is to change the pressure acting on the boundary. Pressures are taken at the source depth $h$. The surface of Mount Mantap is not horizontal of course. I assume it is horizontal and allow the optimum depth to be determined by inversion.

Figure 7

Model source and its mirror image, or virtual source in the free surface

The propagating pressure from the model source is (Blake, 1952; Ziolkowski, 1993)

$$ p(r,t) = \frac{B}{{rc^{2} }}f^{\prime } (\tau ), $$

(16)

where $B$ is the bulk modulus. Continuity of pressure at the boundary $r = a$ of the model source yields

$$ P(t)_{r = a} = p_{g} + \rho gh + p_{atm} - p(t - (2h - a)/c)_{r = (2h - a)} ,\,\,\,t > (2h - a)/c, $$

(17)

in which $p_{g}$ is the pressure exerted by virtue of the tensile strength of the rock, $\rho gh$ is the overburden pressure, $p_{atm}$ is atmospheric pressure, 10⁵ Pa, and $- p(t - (2h - a)/c)_{r = (2h - a)}$ is the free-surface reflection for times $t > (2h - a)/c$.

2.4 Parameters and Ranges

To model each source we require the initial pressure $p_{0} = p_{g} + \rho gh + p_{atm}$, the elastic radius $a$, the density of the elastic medium $\rho$, the P-wave velocity $c$, Poisson’s ratio $\sigma$, and depth $h$. We are going to find the optimum parameters by trial-and-error and need to find sensible ranges for each. In Bayesian statistics these are known as priors.

The five DPRK underground nuclear tests 2 to 6 were located under Mount Mantap in rocks “described as Jurassic-aged granite, but more likely consisting of a variety of rocks, including granite, diorite, gneiss, and possibly quartz porphyry.” (Coblentz & Pabian, 2015, p113). Here we assume the rock is granite. Stowe (1969) made many measurements of the strength and deformation properties of various rocks at Nevada Test Site, including granite. We assume granite is isotropic locally. For our purposes, the key properties of granite are Poisson’s ratio $\sigma = 0.22$, density $\rho = 2,690$ kg m⁻³ and P-wave velocity $c = 5,620$ m s⁻¹. It follows that bulk modulus $B = 4.4353 \times 10^{10}$ Pa. We assume the intact granite at Mount Mantap has these properties. That is, we assume the properties of intact granite are independent of location.

Each explosion is enormous. We expect the strength of the granite mountain to change after each explosion. Perhaps the change is slight, but it must be a decrease. We assume density $\rho$ and bulk modulus $B$ remain constant and expect effective shear modulus to decrease, which means that Poisson’s ratio increases. We assume the lower limit of Poisson’s ratio $\sigma$ to be that of the intact rock, 0.22. Its upper limit is less certain. It must be less than 0.5, because that corresponds to a shear modulus equal to zero: a fluid. We assume its maximum must be in the region of 0.3. We allow $\sigma$ to be an independent parameter for each source, in the range $0.22 \le \sigma \le 0.3$.

We are now not free to choose the P-wave velocity $c$, which is related to Poisson’s ratio and bulk modulus as

$$ c = \left( {\frac{3B(1 - \sigma )}{{\rho (1 + \sigma )}}} \right)^{\frac{1}{2}} . $$

(18)

So $c$ is a dependent parameter.

In Eq. 17, the parameter $p_{g}$ is unknown. Stowe (1969) found the tensile splitting strength of granite to be $1.2 \times 10^{7}$ Pa (1770 p.s.i.). We do not know what value to use, so we allow it to be an independent parameter in the range $0 \le p_{g} \le 1.2 \times 10^{7}$ Pa.

We use the map in Fig. 4 to estimate the depth. The elevation of portal 2 is about 1000 m. We assume the tunnels from portal 2 to the explosions have a gentle uphill gradient of 4% to allow for drainage. We can read the contours from the map in Fig. 4 to determine the elevation of Mt. Mantap above each explosion and so determine an estimate of its depth h, as shown in Table 3. The surface of Mt. Mantap is not horizontal, so the assumption of a planar reflection is an approximation. The source depths h in Table 3 can be regarded as approximate and we allow each depth to have a range, say h− 200: h + 50 m, to the nearest 50 m.

Table 3 Estimation of depths of DPRK tests 2 to 6

The initial pressure $p_{0} = p_{g} + \rho gh + p_{atm}$ is a parameter dependent on the independent parameters $p_{g}$ and $h$.

It is hard to estimate the elastic radius $a$, although approximate estimates may be calculated from the data in Werth and Herbst (1963), if an approximate value of yield is known. We note, however, in Eqs. 11–13 that $a$ is related to P-wave velocity $c$, resonant angular frequency $\omega_{0}$ and, through Blake’s parameter $K$, to Poisson’s ratio $\sigma$. We can estimate the resonant frequency of the P-wave $f_{0} = \omega_{0} /2\pi$ from the seismic data and use Eqs. 11–13 to obtain $a$. That is, we choose $f_{0}$ to be an independent parameter and the dependent parameter $a$ is found as

$$ a = \frac{c}{{4\pi f_{0} }}\frac{{(4K - 1)^{\frac{1}{2}} }}{K}. $$

(19)

We look at the seismograms and their amplitude spectra to estimate the resonant frequencies of the explosions. Richards and Kim (2007) identified the arrivals of the MDJ seismogram recorded on 9 October 2006. Figure 8 shows the Pn arrival for all six events. The number of oscillations in the 7-s window decreases from the smallest event on 25 May 2009 to the largest on 3 September 2017. Note each signal in Fig. 8 has its own amplitude scale. These data are unfiltered. All seismograms shown in this paper are unfiltered. Figure 9 shows the corresponding amplitude spectra including the $\omega^{ - 2}$ decay above resonance expected from Eq. 15. (The MDJ sampling interval for DPRK events 1, 2, 3 and 5 was 0.025 s; for events 4 and 6 it was 0.01 s. The 0.025 s data have been interpolated to 0.01 s.)

Figure 8

Unfiltered Pn arrivals at MDJ for DPRK underground nuclear tests 2 to 6

Figure 9

Amplitude spectra of Pn arrivals. The red dashed line shows the expected $\omega^{ - 2}$ decay of the source spectrum above the resonant frequency

The independent parameters for explosions 2 to 6 and their estimated ranges are given in Table 4.

Table 4 Parameter ranges of the independent parameters for DPRK explosions 2 to 6

2.5 Estimation of the Green’s Function by Deconvolution

A digital seismogram $x(k)$ is the convolution of the source time function $s(k)$ with the Green’s function $g(k)$ plus noise $n(k):$

$$ x(k) = s(k)*g(k) + n(k), $$

(20)

where the asterisk denotes convolution and $k$ is the sample number. The problem is to recover the Green’s function.

We begin with an analytic estimate $f^{\prime } (t)$ of the source time function, which is aliased at the 0.01 s sampling interval of the data. We compute $f^{\prime } (t)$ at 0.001 s samples, convolve it with a 12-pole Butterworth anti-alias filter with 25 Hz cutoff frequency equal to half the Nyquist frequency, 50 Hz, of the data, and resample it to 0.01 s. We call this $\hat{s}(k)$, our estimate of the source time function. The process is illustrated in Ziolkowski (2022). We then compute an approximate inverse filter $\xi (k)$ of $\hat{s}(k)$, such that the convolution of $\xi (k)$ and $\hat{s}(k)$ is a desired wavelet $d(k)$, chosen to be a band-limited delayed Gaussian. That is,

$$ d(k) = \hat{s}(k)*\xi (k). $$

(21)

The delayed Gaussian is shown in Fig. 10. An approximate inverse Wiener filter $\xi (k)$ (Levinson, 1947) is computed for each estimated source time function $\hat{s}(k)$. The desired wavelet $d(k)$ is the same every time. The bandwidth of $d(k)$ was chosen to be as broad as possible with minimum noise and was determined by the lowest-frequency source time function (DPRK6). Deconvolution is then convolution of the seismogram with the inverse filter:

$$ \begin{aligned} \hat{g}(k) =\, & \xi (k)*x(k) = \xi (k)*s(k)*g(k) + \xi (k)n(k) \\ \approx &\, d(k)*g(k) + \xi (k)n(k) \\ \end{aligned} $$

(22)

Fig. 10

Delayed desired Gaussian wavelet

That is, the source time function is replaced by the desired wavelet $d(k)$ and the noise is modified. The function $\hat{g}(k)$ is the estimated Green’s function.

This operation is performed on each of the five MDJ seismograms at each iteration of the search algorithm. The causal inverse filter $\xi (k)$ is short, 100 samples, so the computation is fast. The estimated source time function $\hat{s}(k)$ and the inverse filter $\xi (k)$ are both causal, so the result of their convolution is causal; that is, $d(k) = 0$, k < 0. Ideally, we would like the output to be an impulse at t = 0. We cannot achieve that with a band-limited source time function: the desired output must be band-limited too. We therefore use a delayed zero-phase band-limited approximate impulse, in this case a Gaussian wavelet. The delay must be sufficient to allow the whole wavelet to be causal and is subtracted after the deconvolution.

2.6 Bayesian Approach to Inversion

This section is taken from Ziolkowski (2022). ‘From a statistical point of view, the minimisation problem with a model constraint is equivalent to maximising a conditional probability, given the data measurements. In other words, any probability function that can appropriately describe the behaviour of the expected model can be adopted as a regularisation in the inversion’ (Wang, 2017, p. 68). Bayes’ rule is

$$ p\left( {{\mathbf{m}}|{\mathbf{d}}} \right) = \frac{{p\left( {{\mathbf{d}}|{\mathbf{m}}} \right)p({\mathbf{m}})}}{{p({\mathbf{d}})}}, $$

(23)

where, in this problem, the data ${\mathbf{d}}$ are the five MDJ seismograms for the DPRK nuclear tests 2 to 6, the elements of ${\mathbf{m}}$ are the model parameters of the five sources, $p\left( {{\mathbf{m}}|{\mathbf{d}}} \right)$ is the conditional probability density function (pdf) of the model, given the data, $p\left( {{\mathbf{d}}|{\mathbf{m}}} \right)$ is the conditional pdf of the data, for a given model ${\mathbf{m}},$$p\left( {\mathbf{m}} \right)$ is the pdf of the model, and $p({\mathbf{d}})$ is the pdf of the data. The denominator $p({\mathbf{d}})$ is independent of the model and is usually regarded as impossible to compute for complex problems (e.g. Lambert, 2018, p 115). Sen and Stoffa (2013, p 63) say that, in geophysical problems, $p({\mathbf{d}})$ is a constant and Eq. 23 then becomes

$$ p\left( {{\mathbf{m}}|{\mathbf{d}}} \right) \propto p\left( {{\mathbf{d}}|{\mathbf{m}}} \right)p({\mathbf{m}}). $$

(24)

The constant of proportionality is unknown. The $p\left( {{\mathbf{m}}|{\mathbf{d}}} \right)$ is still a probability density function, however, and is known as the posterior probability density function (PPD) (Sen & Stoffa, 2013). When the measured data ${\mathbf{d}}_{obs}$ are substituted into the expression for the conditional pdf $p\left( {{\mathbf{d}}|{\mathbf{m}}} \right)$, it is called the likelihood function $l\left( {{\mathbf{d}}_{obs} |{\mathbf{m}}} \right)$ (Sen & Stoffa, 2013, p63), and Eq. 24 becomes

$$ p\left( {{\mathbf{m}}|{\mathbf{d}}} \right) \propto l\left( {{\mathbf{d}}_{obs} |{\mathbf{m}}} \right)p({\mathbf{m}}). $$

(25)

The goal is then to find the model parameters ${\mathbf{m}}$ that maximise the PPD $p\left( {{\mathbf{m}}|{\mathbf{d}}} \right)$.

2.7 Model Optimisation

A model m of the five source time functions is specified by the 20 independent parameters of Table 4, each of which is selected at random from its given range. Deconvolution of the five seismograms for the five corresponding source time functions leads to five estimated Green’s functions. The mean of these estimates is $\hat{g}_{m} (k)$. For a given model m and data ${\mathbf{d}}_{obs}$, the normalised root mean square difference between the estimated Green’s functions and this mean is defined as

$$ E({\mathbf{d}}_{obs} |{\mathbf{m}}) = 100\frac{{\sqrt {\sum\limits_{j = 2}^{6} {\sum\limits_{k = 1}^{N} {\left( {\hat{g}(k,j) - \hat{g}_{m} (k)} \right)^{2} } } } }}{{\sum\limits_{j = 2}^{6} {\sqrt {\sum\limits_{k = 1}^{N} {\hat{g}^{2} (k,j)} } } }}, $$

(26)

where $N$ is the number of samples in the Green’s function and $j$ is the event number. This is similar to the normalised root mean square difference of Kragh and Christie (2002) defined for two signals. With this scheme, the mean estimated Green’s function in principle varies with every model.

We define the likelihood function $l\left( {{\mathbf{d}}_{obs} |{\mathbf{m}}} \right)$ as the reciprocal of $E({\mathbf{d}}_{obs} |{\mathbf{m}}):$

$$ l\left( {{\mathbf{d}}_{obs} |{\mathbf{m}}} \right) = \frac{1}{{E({\mathbf{d}}_{obs} |{\mathbf{m}})}}. $$

(27)

The pdf of the model $p\left( {\mathbf{m}} \right)$ needs to be defined. This is our prior knowledge of the model parameters, which is based on many considerations. We allocate a range for each parameter, as indicated in Table 4. We may not have a firm idea about the probability distribution within the range, but may be fairly confident about the limits. Within those limits we can assume a uniform distribution. If the parameter $\eta$ has a lower limit $\eta_{\min }$ and an upper limit $\eta_{\max }$, the value of the uniform pdf is

$$ p(\eta ) = \frac{1}{{\eta_{\max } - \eta_{\min } }}. $$

(28)

for all values of $\eta$ within the limits. The pdf of the model is the product of the pdfs of all the independent parameters,

$$ p(m) = \prod\limits_{k = 1}^{N} {p(\eta_{k} )} = \prod\limits_{k = 1}^{N} {\frac{1}{{\eta_{k\max } - \eta_{k\min } }}} , $$

(29)

which is a constant. Therefore, when all the independent model parameters have uniform probability distributions, maximising the PPD is equivalent to minimising the reciprocal of the likelihood function, which, in our case, is the error.

2.8 Exploring the Parameter Space with Very Fast Simulated Annealing (VFSA)

We have 20 independent parameters in our model. If there are 10 possible values for each parameter, there are 10²⁰ possible combinations of parameters. It is clearly impractical to perform an exhaustive search for the combination that minimises the error. We use very fast simulated annealing (VFSA) to explore the parameter space.

VFSA was proposed by Ingber (1989, 1993). Sen and Stoffa (2013) provide a clear summary with geophysical applications and a pseudo-Fortran code, which I have followed here. The algorithm is in a class of optimization methods that handles an error surface with several peaks and troughs. The optimization process simulates the evolution of a physical system as it cools and anneals into a state of minimum energy. At each temperature $T$, the solid is allowed to reach thermal equilibrium with an energy level given by a Gibbs or Boltzmann probability distribution. The temperature is reduced gradually and exponentially such that in the limit as $T \to 0$ the minimum energy becomes overwhelmingly probable. The uniform distributions used to constrain the model parameters are mapped to suitable temperature-dependent distributions at each temperature. The process starts with an initial temperature and an initial model ${\mathbf{m}}_{0}$ with parameters selected from the defined ranges, in this case Table 4. The initial error $E({\mathbf{m}}_{0} )$ is calculated according to Eq. 26. At each iteration the temperature is reduced slightly, a new model ${\mathbf{m}}_{new}$ is obtained by selecting parameters at random from their uniform distributions, the source time functions are modelled, the seismograms are deconvolved and the error $E({\mathbf{m}}_{new} )$ is calculated according to Eq. 26. If the error is less than last time we have a new model ${\mathbf{m}}_{0} = {\mathbf{m}}_{new}$ with updated error $E({\mathbf{m}}_{0} ) = E({\mathbf{m}}_{new} )$. If it is greater than last time, we accept it with reduced probability. We are searching for the most probable model. As discussed above, for parameters with uniform distributions, this is the model with the smallest error. The starting model can be any legitimate model within the defined constraints.

Figure 11 shows the error $E({\mathbf{m}}_{new} )$ (as $E$) as a function of iteration and the error of the current model $E({\mathbf{m}}_{0} )$ (as $E0$) for a typical run of 1000 iterations, which took less than a minute on a 1.8 GHz laptop. In my limited experience, the algorithm explores the model space efficiently. The final answer is not the same every time, although the final error is very repeatable. I interpret this to mean that the error surface has a number of minima that are very similar: slightly different combinations of parameters produce similar errors. To obtain answers that look reasonable, it is important to determine the boundaries of the model space: that is, the ranges of the independent model parameters, or, in Bayesian statistics, the priors.

Figure 11

a Error E for each iteration; E0 is the error of the current model. b Likelihood for the same VFSA run

We may obtain statistics on the model parameters by running the VFSA over and over again, resulting in different combinations of parameters that yield models with errors and likelihoods very similar to those shown in Fig. 11.

3 Results

3.1 Source Parameters and Source Time Functions

The mean estimated model parameters are obtained from 1000 runs of the VFSA algorithm and shown in Table 5 up to 3-figure precision. The standard error on the mean for each parameter, equal to the standard deviation, divided by the square-root of the number of readings minus one (999), is very small and affects only the third figure. The mean parameters are used to calculate the estimated reduced velocity potential (RVP) source time functions, shown in Fig. 12. In Fig. 12 the kink in the source time function following the initial peak, is the reflection of the peak by the Earth’s surface.

Table 5 Estimated source parameters

Figure 12

Estimated reduced velocity potential source time functions for DPRK tests 2 to 6, with individual scaling. The kink in the curve following the peak is the reflection from the surface

3.2 Yields

Figure 13, from Werth and Herbst (1963) shows reduced displacement potentials for underground nuclear tests at Nevada Test Site (NTS), scaled to 5 kt. The solid curve for granite is the 5 kt Hardhat test; its late-time value at 2 s is about 2500 m³.

Figure 13

Reduced displacement potential functions for four mediums scaled to 5 kilotons (from Werth & Herbst, 1963)

Figure 14 shows the calculated reduced displacement potential (RDP) function, $[ - f(t)]$ in Eq. 8, for DPRK tests 2 to 6, using the estimated mean source parameters of Table 5.

Figure 14

Estimated reduced displacement potential source time functions for DPRK tests 2 to 6, with individual scaling. The kink in the curve at about 0.3 s is arrival of the reflection from the surface

The late-time value of the reduced displacement potential at 2 s, RDPL, was recorded for each source for each of the 1000 runs of the VFSA search and the mean, standard deviation and standard error on the mean obtained. (The theoretical late-time value, obtained from Eq. 10, is $p_{0} a^{3} K/\rho c^{2}$). The yield in kt is then obtained from the granite calibration in Werth and Herbst (1963), using the value of 2500 m³ for 5 kt:

$$ Y = 5RDPL/2500. $$

(30)

The results are summarised in Table 6.

Table 6 Yields of DPRK underground nuclear tests 2 to 6, obtained from estimated reduced displacement potentials (RDPs) and 5 kt RDP for granite Hardhat test in Werth and Herbst (1963)

3.3 Green’s Functions

Figure 15 shows the calculated approximate inverse filters for the source time functions shown in Fig. 12. Convolution of a source time function with its approximate inverse yields the band-limited impulse shown in Fig. 10. The estimated Green’s functions are calculated by convolving each seismogram with the corresponding approximate inverse filter. The results, including the mean estimated Green’s function, are shown in Fig. 16. Figure 17 shows the pn arrival of each Green’s function compared with the mean.

Figure 15

Calculated approximate inverse filters for the source time functions of Fig. 11

Figure 16

Estimated Green’s functions G2 to G6 for events 2 to 6 and mean Gm

Figure 17

Estimated Green’s functions for pn arrival at MDJ for events 2 to 6, compared with the mean Gm, all plotted on the same scale

The Green’s functions appear to be more similar than the seismograms. We can check this by applying Eq. 26 to the seismograms and the Green’s functions. For the 7 s window used for the pn window, the normalised root mean square difference of the seismograms is 51.76; the NRMSD of the Green’s functions is 21.66. That is, the Green’s functions are more similar to each other than the seismograms.

3.4 Map of Elastic Spheres

Finally, Fig. 18 shows the estimated elastic spheres of the DPRK events 2–6 mapped onto the geometry of the official DPRK location map.

Figure 18

Estimated elastic spheres of DPRK nuclear explosions 2 to 6 mapped onto the official layout of Fig. 4, including 1 km squares

4 Test of Method on Seismograms from INCN, South Korea and BJT, China

The method can be tested using data at other seismic stations that recorded the DPRK events. At the suggestion of a reviewer, stations INCN at Incheon, South Korea, and Baijiatuan, (BJT), Bei**g, China, were used. Figures 19 and 20 show the seismograms for DPRK events 2 to 6 obtained from IRIS Data Management Center. DPRK3 is missing from INCN. DPRK2 and DPRK3 are missing from BJT.

Figure 19

DPRK events recorded at INCN; individual amplitude scaling

Figure 20

DPRK events recorded at BJT; individual amplitude scaling

These stations are farther away from Punggye-ri test site than MDJ and the data are noisier. Deconvolution of the seismograms for the corresponding source time functions derived from the MDJ data should recover estimated Green’s functions from the Punggye-ri test site to INCN and BJT. These are shown in Figs. 21 and 22.

Figure 21

Estimated Green’s functions from Punggye-ri test site to INCN on same scale

Figure 22

Estimated Green’s functions from Punggye-ri test site to BJT on same scale

To estimate the similarity of the seismograms or Green’s functions, we apply Eq. 26. For INCN seismograms, using 225 s of data, NRMSD is 75.76 for the seismograms and 47.02 for the Green’s functions. For BJT, using 1200 s of data, NRMSD is 68.56 for the seismograms and 38.41 for the Green’s functions. This corroborates the claim that the derived Green’s functions are more similar than the seismograms.

Figure 23 shows the first 6 s of the seismograms and Green’s functions, side by side, for the recorded events at INCN. Figure 24 shows the first 10 s of the seismograms and Green’s functions, side by side, for the recorded events at BJT. It is evident that the Green’s functions are more similar than the seismograms.

Figure 23

Left: events 2, 4, 5, 6 at INCN ~ 620–68 s on same scale; right: estimated Green’s functions for events 2, 4, 5, 6 at INCN ~ 62–68 s on same scale

Figure 24

Left: events 4–6 at BJT 142–152 s on same scale; right: estimated Green’s functions for events 4–6 at BJT 142–152 s on same scale

5 Discussion

The principle of the method is to confine the parameter space to the source model parameters, assuming the Green’s function from the Punggye-ri nuclear test site to the Mudanjiang seismic station is the same for DPRK nuclear tests 2 to 6. For each model run, a Green’s function is estimated for each source by deconvolution of the corresponding seismogram for the estimated RVP source time function. The differences among the estimated Green’s functions and their mean is treated as the error. Minimisation of the estimated error is achieved by trial-and-error, investigating the parameter space defined by the twenty source parameters and their estimated ranges by very fast simulated annealing (VFSA). An error is defined as a measure of the difference between the measured or calculated value and the true value. As we do not know the true Green’s function, I am unable to use a correct definition of error. Each time the search algorithm is run, the minimum error achieved is about the same, but the parameters obtained are different. I ran the algorithm 1000 times to obtain statistics on the parameters, including mean, standard deviation and standard error on the mean.

The estimated Green’s functions shown in Figs. 16 and 17 are not equal: they vary in amplitude by a factor of about 2. They look similar, however, and are much more similar to each other than the seismograms of Fig. 2. Since the distances separating the sources are small, but not small compared with the wavelengths of the generated seismic P waves, the true Green’s functions are likely to be slightly different. The estimated source time functions may be used to obtain Green’s functions from Punggye-ri nuclear test site to other seismic stations by deconvolution of the corresponding seismograms. This is shown to work for seismic stations: INCN and BJT.

For each model run the reduced displacement potential RDP is also calculated. An estimate of the yield is then obtained using the RDP for the granite Hardhat test provided by Werth and Herbst (1963).

The theory of the analytic model, defined by five parameters for each source, including the assumed density of 2690 kg m⁻³, is obviously a gross over-simplification of the problem. There are several obvious issues: (1) Mount Mantap is not the homogeneous isotropic rock it is assumed to be; (2) the stress regime in Mount Mantap is unknown and is unlikely to be identical with the unstressed rock on which laboratory stress measurements are made; (3) the variation of overburden pressure with depth invalidates the assumption of spherical symmetry. The Appendix shows that the circumference of the elastic sphere is approximately equal to the wavelength of the resonance frequency. If the size of the source were small compared with the wavelength, the shape would not matter: it would behave as a monopole. This is not the case with an explosive source, however: the source size is on the same order as the dominant wavelength. In other words, the shape of the source is significant, but this is ignored by the model. The model includes the surface as a planar reflector, which is a fourth over-simplification: Mount Mantap has significant topography.

A fifth important issue is the effect of the explosions on Mount Mantap. Figure 3 shows Mountap and Fig. 4 shows contours. The elevation of Mount Mantap is 2204 m; the elevation of portal 2 is about 1000 m. It is reasonable to assume the tunnels are close to horizontal with a gentle uphill gradient into the mountain to allow for drainage, and the elevation of each explosion can be estimated, as shown in Table 3. Figure 18 shows the zones of nonlinear deformation defined by the elastic radii. Event 2 is assumed to have been detonated in undisturbed rock. It may have had an effect on the existing stress conditions in Mount Mantap. Event 3 appears to have been in undisturbed rock. As noted by Rodean (1971), these zones absorb at least 95% of the energy of these enormous explosions. Events 4 and 5 are contiguous with events 3 and 2, respectively, and may have been partially decoupled, causing errors in the modelling of events 4 and 5. The proximity of events 4 and 5 to event 6 may have had a decoupling effect on event 6 and application of the theory to event 6 is very likely in error. It is possible that events 4 and 5 were deliberately generated in order to decouple the effects of event 6, at least partially. In any case, it is likely that this part of Mount Mantap was destroyed by the underground nuclear tests before the official destruction of the site on 24 May 2018.

Considering all the sources of error, the method works remarkably well.

The basic assumption of this method is that two or more seismic sources with the same mechanism in essentially the same place share the same Green’s function to any seismic station. If the source time functions can be modelled and the sources are of different size, the method may be applied to earthquakes that satisfy these criteria to invert the seismograms for the source time functions and the Green’s function.

6 Conclusions

I have demonstrated that the new method enables the source parameters, source time functions and yields of DPRK underground nuclear explosions 2 to 6 to be estimated from the seismograms recorded at Mudanjiang (MDJ) seismic station in China, 373 km away. The method assumes the Green’s function from the DPRK Punggye-ri nuclear test site to MDJ is the same for each of the underground nuclear tests 2 to 6. A rigorously determined event location map, corroborated by a map presented by DPRK officials to journalists invited to witness the “destruction” of the site on 24 May 2018, shows that the events were within about 1 km of each other. The explosions were located in Mount Mantap, a granite mountain. Each source was modelled as a spherical cavity in a homogeneous isotropic elastic full space, with five independent parameters for each source constrained by published data on the properties of granite and analysis of the recorded MDJ seismograms. The effect of the ground surface was included as a planar reflection that modified the pressure at the cavity boundary.

Estimated source parameters and source time functions of the five contained DPRK underground nuclear tests have been obtained from the corresponding seismograms recorded at Mudanjiang seismic station. The seismograms were deconvolved for the corresponding estimated source time functions to obtain the estimated Green’s functions. Very fast simulated annealing (VFSA) was used to search the parameter space to minimise the root-mean square difference among the estimated Green’s functions and their mean. The estimated Green’s functions are not identical, but are similar and differ in amplitude by a factor of about 2.

The estimated source time functions may be used to obtain Green’s functions from Punggye-ri nuclear test site to other seismic stations by deconvolution of the corresponding seismograms. This is demonstrated for stations Incheon (INCN), South Korea, and Baijiatuan (BJT), Bei**g, China.

This new approach makes assumptions that are over-simplifications of the problem. Considering this, the method works remarkably well.

The computed zones of nonlinear deformation, which absorb at least 95% of the energy of these enormous explosions, are contiguous. The proximity of events 4 and 5 to the location of event 6 may have had a partial decoupling effect on event 6. In any case, it is likely that this part of Mount Mantap was destroyed by the underground nuclear tests before the official destruction of the site on 24 May 2018.

Appendix

1.1 Relationship Between Resonant Frequency and Model Cavity Dimensions

See Eqs. 31–33 and Fig. 25 here.

From Eqs. 9–11 we have,

$$ \omega_{0} = 2\pi f_{0} = \frac{c}{2Ka}(4K - 1)^{\frac{1}{2}} ,\,{\text{where}}\,K = (1/2)(1 - \sigma )/(1 - 2\sigma ); $$

(31)

This can be rearranged to yield

$$ a = \frac{c}{{2\pi f_{0} L}} = \frac{c}{{4\pi f_{0} }}\frac{{(4K - 1)^{\frac{1}{2}} }}{K} $$

(32)

and

$$ c = f_{0} \lambda ,\,{\text{where}}\,\lambda = 2\pi aL\,{\text{and}}\,L = \frac{2K}{{(4K - 1)^{\frac{1}{2}} }}. $$

(33)

Figure 25 shows $K$ and $L$ plotted as a function of Poisson’s ratio $\sigma$. For a wide range of Poisson’s ratios up to almost 0.4, the value of $L$ is very close to 1 and the wavelength corresponding to the resonant frequency is very nearly equal to the circumference of the source sphere.

Figure 25

$K$ and $L$ plotted as functions of Poisson’s ratio $\sigma$