On the Nature of Potential Energy in Atmospheric Gravity Waves, or Why the Atmosphere Cannot Sustain a Tsunami

Abstract

Motivated by the generation of exceptionally large gravito-elastic waves during the Hunga Tonga–Hunga Ha’apai explosion of 15 January 2022, we examine theoretically the nature of the main air wave branch $GR_0,$ whose undispersed celerity, $\sim 313$ m/s, suggests that it may represent a “tsunami” of the atmospheric column for an effective thickness $H_{eff}\approx 10$ km. However, we find that its potential energy is about 90% elastic across a wide frequency band, thus negating the widely held perception that it constitutes an oscillation between kinetic and gravitational energy. Based on the systematic study of the effect of finite compressibility on the dispersion and potential energy of a classic oceanic tsunami, we confirm that this feature of the branch $GR_0$ stems from the similarity between its celerity and the average speed of sound in the atmosphere. We then show that this similarity is not fortuitous, but rather expected for a perfect gas, which, we conclude, cannot sustain “tsunamis”, i.e., oscillations between kinetic and gravitational energy.

Appendices

Appendix 1

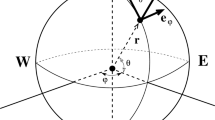
We recall here the definition of the 6 components of the eigenvector of a spheroidal mode in the formalism of Saito (1967, p. 3690), later used by Kanamori and Cipar (1974).

$\bullet$ $y_1 (r)$ represents the vertical (radial) component of particle motion, given as

$$\begin{aligned} u_r (r, \theta , \phi ; \, t) = y_1 (r) \, Y_l^m (\theta , \,\phi ). \end{aligned}$$

(38)

$\bullet$ $y_2 (r)$ represents the radial component of the traction, given as

$$\begin{aligned} \sigma _{rr} (r, \theta , \phi ; \, t) = y_2 (r) \, Y_l^m (\theta , \,\phi ). \end{aligned}$$

(39)

$\bullet$ $y_3 (r)$ represents the orthoradial component of particle motion, given as

$$\begin{aligned} u_{\theta } (r, \theta , \phi ; \, t) = y_3 (r) ~ \frac{\partial \, Y_l^m (\theta , \,\phi )}{\partial \,\theta }. \end{aligned}$$

(40)

$\bullet$ $y_4 (r)$ represents the shear component of the traction, given as

$$\begin{aligned} \sigma _{r\,\theta } (r, \theta , \phi ; \, t) = y_4 (r) ~ \frac{\partial \, Y_l^m (\theta , \,\phi )}{\partial \,\theta }. \end{aligned}$$

(41)

$\bullet$ $y_5 (r)$ represents the change in gravity potential, given as

$$\begin{aligned} \psi (r, \theta , \phi ; \, t) = y_5 (r) \, Y_l^m (\theta , \,\phi ). \end{aligned}$$

(42)

$\bullet$ Finally, $y_6 (r)$ is simply defined as

$$\begin{aligned} y_6 (r) = \frac{d y_5 (r) }{dr} - 4 \pi G\, \rho \, y_1 (r) \end{aligned}$$

(43)

where the $Y_l^m$ are the spherical harmonics of degree l and order m. In all above equations, the time dependence $e^{\,i \omega t }$ has been omitted for simplicity. Obviously, $y_1$ and $y_3$ have dimensions of length, $y_2$ and $y_4$ of pressure, $y_5$ of velocity squared, and $y_6$ of acceleration.

In this fashion, all boundary conditions between spherical shells with different mechanical properties simply require the continuity of the six components of the vector y, with the exception of $y_3$ when at least one of the layers is fluid.

Note that in all fluid layers (outer core, ocean, atmosphere), $y_4$ is identically zero, and $y_3$ becomes a spurious variable

$$\begin{aligned} y_3 = \frac{1}{r \, \omega ^2}\;\left[ g \, y_1 - \frac{y_2}{\rho} - y_5\right] \end{aligned}$$

(44)

so that the differential system becomes 4-dimensional. Also, in a fluid, $y_2$ is simply the opposite of the overpressure during the oscillation.

Finally, for large l and $\theta$ not close to 0 or $\pi ,$ asymptotic expansions of the $Y_l^m$ show that the partial derivative in (40) results in an orthoradial particle displacement $u_{\theta }$ of order $(l\, y_3)$ while the vertical component remains of order $y_1.$

Appendix 2

We summarize here some of the steps in L10’s derivation of his Equations (63) and (66) p. 563. In particular, we emphasize the occasionally different notation used in his paper.

1. Note that L10 orients the vertical axis (which he calls y) downwards with the origin at the top of the atmosphere, which is infinite in the isothermal model and otherwise depends on the particular structure used. On the other hand, we call it z and orient it upwards, with the origin consistently at the bottom of the atmosphere.

2. For a layering of the form (13), L10 does not use the parameter $\phi ,$ but rather defines the [absolute] temperature gradient

$$\begin{aligned} \beta= & {} - \,\frac{d \, \Theta }{dz} = \frac{\phi \,-1}{\phi }\,\cdot \,\frac{\Theta _0}{H} \\= & {} \frac{\phi \,-1}{\phi }\,\cdot \,\frac{g M}{R} \quad (\text {units:}\ \text {K}/\text {km}). \end{aligned}$$

(45)

Conversely,

$$\begin{aligned} \phi =\frac{1}{(1-\beta \,R/Mg)} = \frac{1}{(1-\beta \,H/\Theta _0 )} \end{aligned}$$

(46)

with H defined as

$$\begin{aligned} H= \frac{R\, \Theta _0}{ M \,g } \end{aligned}$$

(12)

(Note that L10’s notation is R for our R/M).

3. Define

$$\begin{aligned} m =\frac{1}{\phi -1} =\frac{\Theta _0}{\beta \,H} -1 =\frac{g M}{R \beta } - 1 \quad (\text {dimensionless}). \end{aligned}$$

(47)

Note that Lamb’s notation is n in L10; m in Lamb (1932).

4. Define h as the full height of the atmosphere

$$\begin{aligned} h =\frac{\Theta _0}{\beta } =\frac{\phi }{\phi -1}\,\cdot \,H =m\,\phi \,H \end{aligned}$$

(48)

where h is defined in Eq. (12). h is equivalent to our $\zeta$ in (16).

5. For the isentropic case $(\phi =\gamma =1.4)$

$$\begin{aligned} \beta =\beta _S =\frac{2}{7}\,\cdot \,\frac{\Theta _0}{H} \quad m=m_S=\frac{5}{2}\quad h=h_S=\frac{7}{2}\,H. \end{aligned}$$

(49)

(L10’s notation: $\beta _S=\beta _1$).

6. For the isothermal case ($\phi =1$)

$$\begin{aligned} \beta= & {} \beta _{\Theta }=0 \\ m= m_{\Theta }\;\;\rightarrow \;\;\infty \quad h=h_{\Theta }\;\;\rightarrow \;\;\infty . \end{aligned}$$

(50)

7. Note that L10 uses V for the celerity of the atmospheric “Lamb” wave (our C), and c for the speed of sound (our $\alpha$).

8. In the course of his derivation, L10 uses the potentially confusing notation $\Pi (x)$ for the factorial: $\Pi (x)=\Gamma (x+1)$ (x real) or x! (x integer), even though the latter had been introduced one century earlier by Kramp (1808).

9. Then, after considerable algebra, L10 derives the solution of the dispersion through the roots of his Equation (63 p. 563) reproduced here as (18), the celerity C of the Lamb wave being given by his Equation (66), reproduced as (19).

In (18) and (19), we prefer the notation $\xi ,$ instead of L10’s $\omega ,$ that dimensionless variable having no relation to an angular frequency.

10. In the limit of large m ($\phi \rightarrow 1$), and in the long-wavelength approximation, $\xi$ is expected to itself be large, and one can use Abramowitz and Stegun’s (1965) Equation (9.3.1) p. 365:

$$\begin{aligned} J_m (z) \approx \frac{1}{\sqrt{2\pi \,m}}\,\cdot \, \left[ \frac{e \,z}{2\,m} \right] ^{\,m}. \end{aligned}$$

(51)

Hence

$$\begin{aligned}{} & {} \frac{z \, J_{m + 1} (z) }{2 \,J_m (z) } = \frac{e\,z^2}{4}\,\cdot \,\sqrt{m / (m+1)}\,\cdot \,\frac{m^m}{(m+1)^{m+1}} \\{} & {} \quad = \frac{e\,z^2}{4\,(m + 1)}\,\cdot \,[m/(m + 1)]^{ m + 1/2}. \end{aligned}$$

(52)

The solution to (17) is then

$$\begin{aligned} \xi ^2=(\beta _S / \beta -1)\,\cdot \,\frac{4 (m +1)}{e}\,\cdot \,[(m + 1)/m]^{m + 1/2} \end{aligned}$$

(53)

and substituting into L10’s Equation (66) p. 563,

$$\begin{aligned} C^2 = g H\,\cdot \frac{e}{(1 + 1/m)^m}\,\cdot \,(1 + 1/m)^{ -1/2}. \end{aligned}$$

(54)

In the limit $m \rightarrow \infty ,$ the fraction in (54) goes to 1, and so does the last term in parentheses, so that $C^2\approx gH,$ which justifies L10’s claim that the celerity of the “Lamb” air wave observed during the Krakatau explosion coincides with that of a would-be tsunami for a column of height H defined by (12). But as shown in the present study, that does not imply that the structure of the wave is that of a tsunami.

However, the approximation (51), on which this result is based, is valid only for large m,  i.e., when the layering is close to isothermal. If, on the opposite, $\phi$ approaches $\gamma$ (isentropic layering; $m \rightarrow 5/2$), then the parenthesis $(\beta _S / \beta - 1) \rightarrow 0$ but $\xi$ will remain finite, in practice close to 7, the first non-zero root of $J_{7/2} (\xi ).$ The celerity of the Lamb wave will also approach 0 as

$$\begin{aligned} C^2\approx (2/7) \,(\beta _S / \beta - 1)\,\cdot \, g H \end{aligned}$$

(55)

which is equivalent to L10’s first [un-numbered] equation on Page 564, except for a typographic error in the parenthesis which is identically zero as typeset in L10.