1 Introduction

Variational Quantum Algorithm [1] (VQA) is a highly promising strategy for achieving quantum advantage, and has found practical applications in optimization problems [2–4], quantum chemistry [5, 6] and quantum machine learning models [7–12]. The performance of VQA is significantly influenced by the structure of the Parameterized Quantum Circuit (PQC). Previous VQAs mainly use manually designed circuits, which highly depend on expert experience. Some VQAs utilize circuit templates [13, 14], which suffer from inflexibility and an abundance of redundant gates.

Quantum Architecture Search (QAS) has been proposed to search the optimal circuit structure for a given variational quantum algorithm [15–23]. Various studies have focused on adopting different search strategies including reinforcement learning [17, 20, 21, 24], evolutionary algorithms [25–27] and simulated annealing [28, 29]. Although these methods are capable of discovering high-performance circuits, their computational cost presents a significant challenge for practical applications since they require calculating the ground-truth performances of a large number of quantum circuits during the search. Consequently, several strategies have been proposed to estimate approximate circuit performances, aiming to accelerate the performance evaluation process. One approach involves training a predictor on a limited set of quantum circuits and their ground-truth performances to estimate circuit performances during the search [16, 30]. Another strategy, known as the super-circuit strategy, estimates circuit performance by directly using shared gate parameters from the super-circuit after one-shot training [31, 32].

The aforementioned methods optimize the circuit structure from scratch for each new task without using any prior experience, rendering this approach inefficient and time-consuming. To address this limitation, a MetaQAS algorithm [33] is proposed to accelerate QAS algorithms by leveraging the prior experience gained from the optimal structures in past tasks. Specifically, MetaQAS learns a meta architecture and gate parameters from a number of training tasks. For a given new VQA, the QAS algorithm initialized with the meta architecture and gate parameters converges much faster than the one initialized with random parameters. However, MetaQAS primarily focuses on learning initialization heuristics for the structure and gate parameters, and needs further optimizations on the structure and gate parameters.

The number of quantum gates in the circuit is an important hyper-parameter in QAS algorithms. Satisfactory performance in VQAs is not achievable with an insufficient number of quantum gates. Conversely, an excessive number of quantum gates introduces significant noise to the quantum circuit. Setting this hyper-parameter traditionally relies on human expert experience. Alternatively, one can incrementally augment the number of quantum gates until the VQA loss falls below a predetermined threshold. However, this approach to gate number exploration is highly time-consuming.

In this paper, we utilize meta-learning to train a circuit generator capable of directly producing high-performance quantum circuits with appropriate structures and gate numbers for new tasks. A quantum circuit is represented as a Directed Acyclic Graph (DAG) [34]. Initially, a Variational AutoEncoder (VAE) is trained on various VQA tasks, learning their corresponding optimal structures through amortized inference. Subsequently, the meta-trained VAE generates high-performance structures directly for new VQA tasks. Additionally, we train a meta-predictor to filter out suboptimal structures from the candidate circuits. Importantly, the training of the meta-generator and meta-predictor is a one-time process applicable to a variety of new tasks. The generator is capable of handling target circuits of varying lengths and generates compiled circuits with different numbers of quantum gates according to the target circuit. Simulation results in variational quantum compiling and QAOA demonstrate that the proposed method yields superior structures compared to a state-of-the-art algorithm, i.e., DQAS [15].

The rest of this paper is organized as follows. In Sect. 2, we present an overview of related work concerning quantum architecture search and meta-learning. The proposed method is detailed in Sect. 3. In Sect. 4, we evaluate the performance of our method by comparing it to a state-of-the-art QAS algorithm. Finally, we summarize the simulation results and discuss potential future directions in Sect. 5.

2 Related works

This section describes the related work on quantum architecture search and meta-learning.

2.1 Quantum Architecture Search (QAS)

QAS has garnered considerable attention due to the significant impact of the circuit structure on the performance of Variational Quantum Algorithms (VQAs). In contrast to manually designed circuits, QAS based on machine learning techniques automatically generates high-performance circuits with fewer quantum gates and shallower depth [16–18, 21]. QAS algorithms primarily comprise a search module and an evaluation module. The search module defines the search strategy to seek improved structures, while the evaluation module calculates the performances of quantum circuits, providing feedback for the search module. Previous studies focus on the search module and have proposed QAS algorithms based on various approaches including reinforcement learning [17, 20, 21, 24], evolutionary algorithms [25–27], simulated annealing [28, 29], and gradient descent [15]. However, these algorithms require calculating the performances for a large number of circuits during the search process, incurring substantial computational costs.

In order to accelerate the QAS algorithm, various evaluation strategies have been proposed to estimate the approximate performances of quantum circuits instead of the ground-truth ones. These strategies include the predictor-based method [16, 30] and weight-sharing strategy [31, 32]. Zhang et al. introduced an RNN-based predictor to estimate circuit performance, trained on a limited number of quantum circuits and their corresponding ground-truth performances [16]. However, modeling the extensive circuit space remains a significant challenge. In the weight-sharing strategy, a SuperCircuit is trained through one-shot training, involving the sampling of SubCircuits from the SuperCircuit and updating their parameters accordingly. Subsequently, the performances of SubCircuits are estimated by directly using the parameters inherited from the SuperCircuit instead of individually training each SubCircuit. Nonetheless, the optimization of the SuperCircuit poses a challenge due to the substantial variance in the sampled SubCircuits. Furthermore, it cannot be guaranteed that the performance of a quantum circuit with inherited parameters is strongly correlated with the one that is trained individually.

2.2 Meta-learning

When learning new skills, humans rarely start from scratch. Instead, they often draw upon experiences and abilities gained from previous related tasks. This approach enables fast learning of new skills [35]. Likewise, meta-learning, also known as “learning to learn”, is a machine learning technique that leverages prior learning experiences to accelerate the learning process for new tasks [36]. Meta-learning has demonstrated significant success across various domains, including image recognition [37], recommendation systems [38], speech recognition [39] and neural architecture search [40].

Meta-learning has found applications in the domain of quantum machine learning, demonstrating satisfactory performance in tasks such as learning to find approximate optima of the gate parameter for quantum circuits [41–43]. Beyond gate parameters, meta-learning is also employed to learn good initialization heuristics for quantum circuit architectures [33].

3 Method

We propose an efficient QAS algorithm for Variational Quantum Algorithms (VQAs), leveraging prior knowledge acquired from a variety of training tasks. In this section, we delineate the process of searching for optimal quantum circuits in the context of a typical VQA, namely, variational quantum compiling. Just as programs must be compiled into machine code for classical computers, quantum algorithms must be compiled before execution on Noisy Intermediate-Scale Quantum (NISQ) devices, considering specific constraints like native gates. Variational quantum compiling aims to convert a given target quantum circuit or unitary \(U_{t} \) into a compiled circuit \(U_{c}(\boldsymbol{\theta })\) constructed by the native gates of the NISQ device, ensuring functional equivalence with the target circuit. θ represents the trainable gate parameters of the compiled circuit \(U_{c}\).

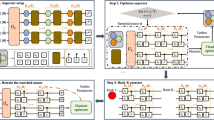
The proposed method comprises two primary steps: meta-training and meta-test, as shown in Fig. 1. During the meta-training phase, a generator is trained on a variety of tasks \(\mathcal{D}=\{(\mathcal{G}_{t}^{i}, \mathcal{G}_{c}^{i})\}_{i=1}^{N_{ \tau}}\) with meta-learning, where \(N_{\tau}\) represents the number of training tasks. Each training task includes a target circuit \(\mathcal{G}_{t}^{i}\) and its corresponding ground-truth compiled circuit \(\mathcal{G}_{c}^{i}\). The compiled circuit is constructed using native gates of the NISQ device, ensuring functional equivalence with the target circuit. The difference between the target and the complied circuits is assessed using the Local Hilbert-Schmidt Test (LHST) [28]. The compiled circuit for a given target circuit can be obtained from benchmarks, historical tasks, or generated using any QAS algorithm. This paper employs a representative QAS algorithm, namely DQAS [15], to search for the compiled circuit. As depicted in Fig. 1, the generator is composed of a graph encoder \(q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathcal{G}_{t})\) and a graph decoder \(p_{\boldsymbol{\varphi}}(\mathcal{G}_{c}\mid \mathbf{z})\) where ϕ and φ are trainable parameters of the encoder and decoder, respectively. For each training task, the generator encodes the target circuit \(\mathcal{G}_{t}\) into a latent vector z using the encoder \(q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathcal{G}_{t})\) and subsequently decodes a circuit \(\mathcal{G}_{c}'\) from z by the decoder \(p_{\boldsymbol{\varphi}}(\mathcal{G}_{c}\mid \mathbf{z})\). Our objective is to encourage the generated circuit \(\mathcal{G}_{c}'\) derived from the latent vector of the target circuit to approximate the ground-truth compiled circuit \(\mathcal{G}_{c}\).

Figure 1
figure 1

Overview of the proposed QAS algorithm for VQAs

Full size image

We meta-train the generator to minimize the approximated evidence lower bound (ELBO) for each task through amortized inference

$$ \begin{aligned} \min _{\boldsymbol{\phi , \varphi}} \sum _{(\mathcal{G}_{t}, \mathcal{G}_{c}) \sim \mathcal{D}} (-\mathbb{E}_{\mathbf{z} \sim q_{ \boldsymbol{\phi}}\left (\mathbf{z} \mid \mathcal{G}_{t}\right )}( \log p_{\boldsymbol{\varphi}}\left (\mathcal{G}_{c} \mid \mathbf{z} \right )) +\lambda \cdot \operatorname{KL}(q_{\boldsymbol{\phi}} \left (\mathbf{z} \mid \mathcal{G}_{t}\right ) \| p(\mathbf{z}))). \end{aligned} $$
(1)

The first term quantifies the difference between the generated circuit and the ground-truth compiled one. The latter term represents Kullback-Leibler(KL) divergence between two distributions. We align the distribution \(q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathcal{G}_{t})\) with the prior distribution \(p(\mathbf{z}) \) by minimizing the KL divergence, where \(p(\mathbf{z}) \) is a standard normal distribution. λ serves as a weighted parameter that balances the losses between the circuit difference and the KL divergence. The optimization problem can be solved by stochastic gradient variational Bayes [44]. During the meta-training process, the teacher forcing strategy [45] is employed to calculate the difference between the generated circuit and the ground-truth compiled one.

Once the generator is trained, it can be used to generate compiled circuits for various unseen target circuits during the meta-test step. Notably, the target circuit differs from those used in the training step. When presented with a new target circuit, the graph encoder \(q_{\boldsymbol{{\phi}^{*}}}(\mathbf{z} \mid \mathcal{G}_{t})\) is employed to calculate the latent vector z of this circuit. Subsequently, the decoder \(p_{\boldsymbol{{\varphi}^{*}}}(\mathcal{G}_{c} \mid \mathbf{z})\) generates a set of candidate compiled circuits based on the target circuit’s latent vector z according to Algorithm 1. In the final validation step, the candidate circuit with minimal loss after optimizing the gate parameters is designated as the final compiled circuit.

Below, we provide a comprehensive elucidation of the circuit representation as well as the structures of the encoder and decoder.

3.1 Circuit representation

We use a Directed Acyclic Graph (DAG) to represent a quantum circuit. A node describes a quantum gate and the qubit(s) it operates on, denoted by “\(\mathit{Gate}\text{--}{Qubit(s)}\)”. For example, “\(\mathit{CNOT}\text{--}{q_{1}q_{2}}\)” represents a controlled-not gate acting on qubits \({q_{1}}\) and \({q_{2}}\). A directed edge signifies the output-input relationship between two gates. For example, the directed edge from “\(\mathit{Rz}\text{--}{q_{1}}\)” to “\(\mathit{CNOT}\text{--}{q_{1}q_{2}}\)” indicates that the output of “\(\mathit{Rz}\text{--}{q_{1}}\)” is fed into “\(\mathit{CNOT}\text{--}{q_{1}q_{2}}\)”. In other words, each edge represents the flow of information within a particular qubit. We add a start node \(\mathit{Start}\text{--}{\{q_{i}\}_{i=1}^{N}}\) and an end node \(\mathit{End}\text{--}{\{q_{i}\}_{i=1}^{N}}\) to simulate the input and output of the quantum circuit. Figure 2 provides an illustration of the DAG representation of a quantum circuit, with a length (L) of 5 and a depth (D) of 4. The DAG has 7 nodes, including a Start and an End nodes. The blue, green, and black paths in Fig. 2(b) denote the information flow of qubits 1, 2, and 3, respectively. The DAG effectively encapsulates the structure details of the quantum circuit, including the types of quantum gates and their interconnections. Through the DAG representation, we can extract the structure information of a quantum circuit using graph models [46].

Figure 2
figure 2

An example of the DAG representation of a quantum circuit

Full size image

3.2 Encoder

The encoder \(q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathcal{G}_{t})\) converts the target circuit represented by a DAG \(\mathcal{G}_{t}\) into a latent vector z. The encoding of the target circuit is performed using a Graph Neural Network (GNN) employing an asynchronous message-passing scheme. In contrast to traditional synchronous message passing, where all nodes simultaneously receive and process messages from their neighbors at each step, asynchronous message passing allows nodes to update their hidden states at different times independently. In this encoding strategy, the calculation of a node’s hidden state relies on the hidden states of all its predecessors, mimicking the computational routine of a quantum circuit operating on quantum data. The hidden state \(\mathbf{h}_{v}\) of each node v in \(\mathcal{G}_{t}\) is denoted as

$$ \begin{aligned} \mathbf{h}_{v}=\mathcal{U}\left (\mathbf{x}_{v}, \mathbf{h}_{v}^{ \text{in}}\right ), \end{aligned} $$
(2)

where \(\mathcal{U}\) is an update function, implemented through a Gated Recurrent Unit (GRU) model [47]

$$ \begin{aligned} \mathbf{h}_{v}=\mathit{GRU}_{e}\left (\mathbf{x}_{v},\mathbf{h}_{v}^{ \text{in}}\right ). \end{aligned} $$
(3)

\(\mathbf{x}_{v}\) is a one-hot vector of the node v, signifying an operation by considering both the quantum gate type and the operated qubit. The input state for node v can be calculated by \(\mathbf{h}_{v}^{\mathrm{in}}=\mathcal{A}\left (\left \{\mathbf{h}_{u}: u \rightarrow v\right \}\right )\), where \(\mathcal{A}\) is an aggregation function and \(u \rightarrow v\) signifies the presence of a directed edge from node u to node v. The set \(\{\mathbf{h}_{u}: u \rightarrow v\}\) comprises the hidden states of v’s predecessors. The aggregation function \(\mathcal{A}\) can be implemented by a gated sum function

$$ \begin{aligned} \mathbf{h}_{v}^{ \text{in}}=\sum _{u \rightarrow v} g_{e}\left ( \mathbf{h}_{u}\right ) \odot m_{e}\left (\mathbf{h}_{u}\right ), \end{aligned} $$
(4)

where \(g_{e}\) represents a gating network implemented by a single linear layer followed by a \(sigmoid \) activation function. \(m_{e}\) is a map** network implemented by a single linear layer without bias and activation function. ⊙ denotes element-wise multiplication. The position information of previously connected nodes is also considered in the calculation of \(\mathbf{h}_{v} \)

$$ \begin{aligned} \mathbf{h}_{v}^{\text{in}}=\sum _{u \rightarrow v} g_{e}\left ( \mbox{Concat}(\mathbf{h}_{u},\mathbf{x}_{\text{pos}})\right ) \odot m_{e} \left (\mbox{Concat}(\mathbf{h}_{u},\mathbf{x}_{\text{pos}})\right ), \end{aligned} $$
(5)

where \(\mathbf{x}_{\text{pos}} \) denotes a one-hot vector representing the global position of node u. We set \(\mathbf{h}_{v}^{\text{in}}\) of the Start node to be a zero vector as the Start node has no predecessor node. The hidden state of the End node is used to represent the graph, i.e., \(\mathbf{h}_{\mathcal{G}_{t}}=\mathbf{h}_{v_{End}}\).

The encoding process mimics the evolution of an input quantum state through a quantum circuit, with \(\mathbf{h}_{v}\) representing the output state at each gate. In addition to the forward encoding, we adopt a reverse encoding [48] to comprehensively extract structure information from the DAG, where the directions of all edges are reversed. Two GRUs are used to obtain the forward and the backward hidden states (\(\boldsymbol{h}_{f}\) and \(\boldsymbol{h}_{b}\)), respectively. These states are concatenated, and a trainable linear layer is utilized to reduce the dimension of the resulting vector by half. The output vector is used to denote the hidden state of the graph \(\boldsymbol{h}_{\mathcal{G}_{t}} \).

We take \(\mathbf{h}_{\mathcal{G}_{t}}\) as the input for two linear layers \(\mathrm{NN}_{\boldsymbol{\mu}} \) and \(\mathrm{NN}_{\boldsymbol{\sigma}} \) to obtain a mean vector μ and a standard deviation vector σ as shown in Fig. 3. Subsequently, the latent vector z can be sampled from a circuit-conditioned Gaussian distribution, i.e., \(\mathbf{z} \sim q_{ \boldsymbol{\phi}}\left (\mathbf{z} \mid \mathcal{G}_{t}\right ) = \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma _{i}}^{2})\). By using the reparameterization trick, z can be represented as \(\mathbf{z}=\boldsymbol{\mu}+\boldsymbol{\sigma} \odot \boldsymbol{\epsilon}\), where \(\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \). The latent vector z serves as an embedding of \(\mathcal{G}_{t} \) in the latent space \(\mathcal{Z} \).

Figure 3
figure 3

The structure of the encoder

Full size image

3.3 Decoder

Given a latent vector z, the graph decoder \(p_{\boldsymbol{{\varphi}}}(\mathcal{G} \mid \mathbf{z})\) generates a DAG \(\mathcal{G}\) representing a quantum circuit. The detailed process is shown in Algorithm 1. Initially, we add a \(start\) node \(v_{0}\) to the graph \(\mathcal{G}\). A single linear layer \(\mathrm{NN}_{init} \) with a tanh activity function is used to calculate the hidden state \(\mathbf{h}_{v_{0}}\) of the Start node \(v_{0}\). Subsequently, the decoder constructs a graph \(\mathcal{G}\) by progressively sampling and adding a new node \(v_{i}\) at each step until an \(End\) node is sampled or the circuit length reaches the specified maximum.

Algorithm 1
figure a

Graph generation by a decoder

Full size image

To generate a new node \(v_{i}\), the following steps are executed. Initially, a node \(v_{i}\) is sampled based on the probability distribution determined by the hidden state of the preceding node \(v_{i-1}\), i.e., \(\boldsymbol{p}=\iota (\mathbf{h}_{v_{i-1}})\). ι is a single linear layer followed by a softmax function. The newly sampled node \(v_{i}\) encompasses details such as gate type and the qubit(s) it operates on. Depending on the operated qubit(s), appropriate directed edges are incorporated into the DAG. Finally, the hidden state \(\mathbf{h}_{v_{i}}\) of node \(v_{i}\) is calculated by a Gated Recurrent Unit \(\mathit{GRU}_{d}\), which has the same structure with the one \(\mathit{GRU}_{e}\) in the encoder.

3.4 Meta-predictor for fast evaluation

In the meta-test step, the meta-trained generator produces a set of candidate compiled circuits for the target circuit. During the final validation process, the optimal circuit is determined by assessing the ground-truth performance of these candidate circuits. For variational quantum compiling, the performance of a quantum circuit is measured by the compiling loss. However, the calculation of ground-truth performance is time-consuming as it requires the optimization of gate parameters until convergence. Similar to Predictor-based Quantum Architecture Search (PQAS) [16], we can approximate the performance of the candidate circuits using a predictor to accelerate the final validation process. However, the predictor used in PQAS is task-specific and requires retraining for each new task, making it inefficient. To address this problem, we train a meta-predictor using a variety of tasks \(\mathcal{D}_{pre}\). The meta-trained predictor can estimate the performance of quantum circuits for various target circuits. Each training sample consists of a target circuit, a compiled circuit, and the corresponding compilation loss, denoted as \(\mathcal{G}_{t} \), \(\mathcal{G}_{c} \), and s. The compilation loss is measured by the Local Hilbert-Schmidt Test (LHST) [28] between the target circuit and the compiled one. The structure of the predictor is depicted in Fig. 4. The DAGs \(\mathcal{G}_{t} \) and \(\mathcal{G}_{c} \) are initially transformed into hidden vectors \(\mathbf{h}_{\mathcal{G}_{t}}\) and \(\mathbf{h}_{\mathcal{G}_{c}}\) using two graph neural networks, employing structures identical to those utilized in the encoder. \(\mathbf{h}_{\mathcal{G}_{t}}\) and \(\mathbf{h}_{\mathcal{G}_{c}} \) are fed into two linear layers with relu activation function to obtain the predicted loss \(f_{\boldsymbol{\omega}}(\mathcal{G}_{t}, \mathcal{G}_{c})\), where ω are trainable parameters of the predictor. The predictor is trained by minimizing the Mean-Squared Error (MSE) between the predicted compilation loss and the ground-truth one

$$ \begin{aligned} \min _{\boldsymbol{\omega}}\sum _{(\mathcal{G}_{t}, \mathcal{G}_{c}, s) \sim \mathcal{D}_{pre}}\left (s-f_{\boldsymbol{\omega}}(\mathcal{G}_{t}, \mathcal{G}_{c})\right )^{2}. \end{aligned} $$
(6)
Figure 4
figure 4

The structure of the predictor

Full size image

4 An extension of our method on QAOA

In Sect. 3, we provided a detailed description of our proposed method in the context of variational quantum compiling. This approach is readily adaptable to other variational quantum algorithms. In this section, we illustrate the application of our method to QAOA, focusing specifically on the MaxCut problem.

As illustrated in Fig. 1, our method encodes a VQA task into a latent vector z using an encoder. In the context of quantum compiling, each task refers to a target circuit to be compiled. The target circuit is represented by a directed acyclic graph. For task encoding in quantum compiling, we use a Graph Neural Network (GNN) based on an asynchronous message-passing scheme. However, in QAOA, each task corresponds to a MaxCut problem, depicted by an undirected graph. To achieve a latent representation invariant to the isomorphic MaxCut problem, we design the encoder using a Graph Isomorphism Network (GIN) [49]. In the context of QAOA, we only need to replace the GNN in the encoder of Fig. 3 and the first GNN for task encoding in the predictor of Fig. 4 with a GIN. Similarly to quantum compiling, the generator is trained by minimizing the approximated evidence lower bound (ELBO) for each task through amortized inference. The meta-predictor is trained to minimize the Mean-Squared Error (MSE) between the predicted and ground-truth numbers of cuts. We normalize the number of cuts by dividing it by the theoretical maximum, scaling it between 0 and 1.

We represent a MaxCut task by an adjacency matrix A and a degree matrix X. The degree matrix describes the degree of each node. Each row is a one-hot vector representing the degree of a node. Figure 5 illustrates an example of the graph representation of a MaxCut problem. A 4-layer GIN is used to generate the node embedding matrix H. The embedding matrix in the i-th layer is defined as

$$ \mathbf{H}^{(i)} = \text{MLP}^{(i)}((1+\varepsilon ^{(i)}) \cdot \mathbf {H}^{(i-1)} + \mathbf{A}\mathbf {H}^{(i-1)}), $$
(7)

where \(\mathbf {H}^{(0)} = \mathbf {X}\), and the term “MLP” refers to a multi-layer perception with the Linear-Batchnorm-ReLU structure. The parameter ε represents a learnable bias. Finally, the hidden state of the MaxCut problem is obtained by summing the embeddings of all nodes, i.e., summing up all rows of the matrix \(\mathbf {H}^{(4)}\). This hidden state encapsulates the collective information of the MaxCut problem.

Figure 5
figure 5

An example of the representation of a MaxCut task

Full size image

5 Numerical simulation

We present the simulation results of the meta-trained generator and predictor applied to variational quantum compiling in Sect. 5.1. Additionally, Sect. 5.2 shows the simulation results of our proposed method on Quantum Approximate Optimization Algorithm (QAOA). We conduct a performance comparison between our proposed method and the state-of-the-art QAS algorithm, namely DQAS [15].

5.1 Simulations on variational quantum compiling

5.1.1 Settings

We conducted the simulations on a classical computer equipped with a CPU i9-10900K, employing the Pennylane [50] framework, which encompasses a wide range of quantum machine learning libraries. We consider target circuits with 3 qubits. The target circuits are composed of 4, 5, or 6 quantum gates, randomly selected from the gate set \(\mathcal{A}_{\mathit{target}}=\){H, X, Y, Z, S, T, \(\mathit{R_{X}}(\theta )\), \(\mathit{R_{Y}}(\theta )\), \(\mathit{R_{Z}}(\theta )\), CNOT, CZ, CY, SWAP, Toffoli, CSWAP}, operating on randomly chosen qubits. The native gate set for variational quantum compiling is \(\mathcal{A}_{\mathit{native}}=\){\(\mathit{R_{X}}(\pi , \pm \pi /2)\), \(\mathit{R_{Z}}(\theta )\), \(\mathit{CRZ}(\theta )\), CZ, \(\mathit{XY}(\theta )\)}, which is employed in Rigetti’s Aspen-11 quantum processor. \(\mathit{R_{X}}(\theta )\) and \(\mathit{R_{Z}}(\theta )\) are rotation gates by an angle θ about the x-axis and z-axis of the Bloch sphere. \(\mathit{CRZ}(\theta )\) a two-qubit gate that applies a phase rotation of θ to the \(|11\rangle \) state. CZ is a \(\mathit{CRZ}(\theta )\) operation applied with a rotation parameter \(\theta = \pi \). \(\mathit{XY}(\theta )\) is a two-qubit gate that applies a coherent rotation of θ to the \(|01\rangle \) and \(|10\rangle \) states. We set the maximum length of the compiled circuit to 30.

Each training sample comprises a target circuit and its optimal compilation using native gates. The training dataset is composed of target circuits with varying lengths, i.e., \(L=4, 5, 6\). Specifically, we randomly generate 1000 target circuits for each length, resulting in a total of 3000 target circuits in the training set. In this paper, we employ the DQAS algorithm [15] to obtain the optimal compilations for the target circuits. It’s important to emphasize that alternative QAS algorithms can also be utilized for this purpose. We search the compiled circuit for each target circuit by gradually increasing the length of the compiled circuit until the loss drops below 0.05 or the circuit length reaches 5L. If the loss of the compiled circuit with 5L gates is higher than 0.05, we abandon the respective target circuit as we cannot find a compiled circuit within the specified length.

The generator and the predictor are trained using the Adam optimizer [51]. The training of the generator took 1.57 hours. The hyper-parameters of the proposed method are shown in Table 1.

Table 1 The hyper-parameters of our method on quantum compiling
Full size table

5.1.2 Performances of different sampling strategies

We assess the performance of the trained generator using 300 target circuits that do not exist in the training set. For each test circuit, the generator produces 100 candidates for the compiled circuit. Subsequently, we compute the LHST loss [28] for each candidate circuit after optimizing its gate parameters and output the one with the lowest LHST loss. As described in Sect. 3.3, the graph decoder generates a circuit by sequentially choosing candidate gates from the native gate set based on the probability distribution of candidate gates. We explore various sampling strategies, including stochastic and top-k sampling schemes [52], where \(k=10, 15, 20, 25\). In stochastic and top-k sampling, the decoder selects quantum gates from all the candidate gates and the top k candidate gates with the highest probabilities, respectively.

Table 2 presents the average loss of the proposed method, along with the length (L) and the depth (D) that represent the number of quantum gates and layers. Among the schemes explored, the stochastic approach yields the lowest loss. However, it results in compiled circuits with more quantum gates and larger depth. In contrast, In the top-k scheme, the loss decreases as k increases, accompanied by an increase in the number of gates within the compiled circuit. However, the depths of the compiled circuits remain similar across varying values of k. The top-k scheme effectively balances the loss and circuit depth. Considering both the compiling loss and circuit depth, we opt for the top-25 strategy in the following simulations.

Table 2 The average loss of compiling 300 target circuits with the proposed generator
Full size table

We also present the uniqueness of the generated circuits in Table 2, quantified as the percentage of unique circuits in the generated set. Notably, all strategies exhibit a uniqueness exceeding 97.7%, affirming the remarkable diversity of quantum circuits generated by the generator. This diversity empowers the generator to produce a wide array of candidate circuits for final validation. Additionally, we show the novelty of the generated circuits, defined as the percentage of circuits that do not exist in the training set. The novelties of all strategies are 100.00%, indicating that the generated circuits are entirely distinct from those in the training set.

In previous simulations, we assume that qubits are fully connected. However, qubit connectivity is typically limited in the NISQ era. Specifically, we consider a chain connection, denoted as \({q_{1}}\text{--}{q_{2}}\text{--}{q_{3}} \), and use the meta-trained generator to produce circuits within this constrained connectivity. The search space in the chain connection is a subspace of the fully connected one. Notably, there is no necessity to collect new training data or retrain the generator for this scenario. Instead, a mask code can be added to guide the generator in selecting permitted operations within the limited connections. The simulation results for this chain-connected scenario are shown in Table 3. The average losses under limited connections closely resemble those under full connectivity. However, due to the prohibition of a direct connection between \({q_{1}}\) and \({q_{3}}\), a greater number of gates and larger depth are required.

Table 3 The average losses for compiling 300 target circuits with the meta-trained generator under the chain connection
Full size table

5.1.3 Performance of the meta-predictor

We train a meta-predictor to accelerate the proposed method by filtering out generated circuits with suboptimal performance. Each training sample of the predictor comprises a target circuit \(\mathcal{G}_{t} \), a compiled circuit \(\mathcal{G}_{c} \) and the associated compilation loss s. The training set should contain compiled circuits with various performances. To achieve this, we use the 3,000 training samples of the generator and calculate their respective losses. In addition, we also collect 207,000 target circuits by randomly selecting 4, 5, and 6 gates from \(\mathcal{A}_{\mathit{target}}\) and choosing the operated qubits at random. Their compiled circuits are generated by randomly selecting \([2L, 5L]\) gates from \(\mathcal{A}_{\mathit{native}} \) and randomly choosing the operated qubits, where L represents the number of quantum gates in the target circuit. The total 210,000 samples are randomly divided into the training and test sets for the predictor, comprising 200,000 training samples and 10,000 test samples, respectively. The predictor is trained for 100 epochs.

The Pearson correlation coefficient between the predicted and the ground-truth compilation losses on the 10,000 test samples is 0.784, indicating a strong correlation. For ease of visualization, we illustrate the predicted and ground-truth losses of 1,000 randomly selected test samples in Fig. 6.

Figure 6
figure 6

The relationship between the predicted loss and the ground-truth one

Full size image

We also depict the loss distributions for 10,000 test samples and the subset obtained by removing samples with predicted losses exceeding 0.1 in Fig. 7. Notably, the predictor effectively filters out suboptimal compiled circuits while retaining those exhibiting high performance.

Figure 7
figure 7

The loss distributions of 10,000 test samples (blue bars) and the remaining samples filtered by the predictor (red bars)

Full size image

5.1.4 Comparison with DQAS

We conduct a performance comparison between the proposed method and a state-of-the-art QAS algorithm, specifically DQAS [15], in terms of compilation loss and running time. As the circuit length L is a hyper-parameter for DQAS, we gradually increase L until the compilation loss is below 0.05 or the circuit length reaches 30. The simulation results are summarized in Table 4. The proposed methods consistently demonstrate lower compilation losses compared to DQAS. With the top-25 scheme (Gen-top-25), the average length and depth of compiled circuits are comparable to those of DQAS. Employing the stochastic scheme (Gen-stochastic) results in the lowest loss, specifically 0.0075, which is merely a quarter of DQAS’s loss. However, this comes at the cost of using 8 more gates, resulting in a 4-unit increase in depth. By using the meta-predictor (Gen-pred-top-25 and Gen-pred-stochastic), the compilation loss is only slightly higher than that using the ground-truth loss in the final validation, demonstrating the feasibility of using a meta-predictor.

Table 4 Simulation results of different QAS algorithms on quantum compiling. “gen” and “pred” denote the generator and predictor, respectively
Full size table

Table 5 presents the running times of various QAS algorithms. We define the times for searching the optimal structure and fine-tuning the gate parameters as \(t_{s}\) and \(t_{f}\), respectively. The running time of estimating the performance by the predictor is denoted as \(t_{p}\). \(t_{total}\) represents the total running time of each algorithm. DQAS takes 8.36 hours to search for the optimal structure, while the proposed method generates candidate compiled circuits in just 1 second. In our method, the fine-tuning step takes more time than DQAS due to the need to fine-tune gate parameters for a set of candidate circuits. The total runtimes of our proposed method with the top-25 and stochastic schemes are 13.35 and 15.15 minutes, respectively, which are only 2.6% and 3.0% of the time consumed by DQAS. The predictor requires less than half a second to predict the performance of candidate circuits. By filtering out candidate circuits with unsatisfying performances, we can significantly reduce the running time in the fine-tuning step, thereby halving the total running time.

Table 5 Running times of compiling 90 target circuits with different QAS algorithms
Full size table

5.2 Simulations on QAOA

In this section, we solve the MaxCut problem involving 8 nodes using the Quantum Approximation Optimization Algorithm (QAOA). The Max-Cut problem is a classical combinatorial optimization problem. It involves the task of optimally dividing the nodes of a graph into two distinct sets in such a way that the number of edges connecting these sets is maximized.

Given a MaxCut problem, our proposed method aims to search for high-performance circuits for QAOA. In QAOA for the MaxCut problem, each qubit represents a node of the graph, resulting in an 8-qubit quantum circuit. We use the gate set {\(\mathit{R_{Y}}(\theta )\), \(\mathit{R_{Z}}(\theta )\), CNOT}, and limit the number of gates (L) in the circuit to fall within the range of 4 to 12. Following QAOA, we prepare the input state \(|+\rangle ^{\otimes 8}\) by applying a layer of Hadamard gates.

We randomly generate 1100 distinct graphs (i.e., MaxCut problems) with 8 nodes using the Erdős-Rényi model [53], where the probability of edge creation is set to 0.5. We use 1000 graphs to train the generator, and the remaining 100 are used to validate the generator’s performance. It is worth noting that the MaxCut tasks during testing differ from those during training. During the meta-training phase, the optimal circuit for each MaxCut task is obtained through random search rather than employing the DQAS algorithm in the simulation of quantum compiling. Specifically, we randomly select 50 quantum circuits from the search space, each composed of 4 gates. Subsequently, we compute the number of cuts via QAOA using these circuits. The circuit that achieves the theoretical maximum cut for the MaxCut problem is identified as the optimal circuit. If no circuit achieves the theoretical maximum cut, we increment the number of gates in the quantum circuit by one and repeat the aforementioned process by randomly selecting another set of 50 circuits.

The hyper-parameters of the proposed method in this simulation are shown in Table 6. Table 7 shows the simulation results of our methods and DQAS on QAOA. As the circuit length L is a hyper-parameter for DQAS, we gradually increase L until the theoretical maximum cut is obtained or the circuit length reaches 12. Success rate refers to the proportion of tasks, out of 100 MaxCut tasks, in which the theoretical maximum cut value is found. The success rates of our method (Gen-top-15) are 97%, significantly surpassing DQAS’s 74%. We also train a meta-predictor with 4500 samples. By using a predictor (Gen-pred-top-15), the computational cost for calculating the ground-truth performance of candidate circuits is notably reduced to only 20.3% compared to the method without a predictor (Gen-top-15). The success rate remains at 93%, with only a marginal decrease compared to the one without a predictor. The table also displays the average number of cuts among 100 MaxCut tasks. The average numbers of cuts achieved by our methods exceed that of DQAS by more than 0.85.

Table 6 The hyper-parameters of our method on QAOA
Full size table
Table 7 Simulation results of different QAS algorithms on QAOA. “gen” and “pred” denote the generator and predictor, respectively
Full size table

The performance of the candidate circuits generated by the aforementioned generator is evaluated in noisy environments. We consider 0.1% and 1% depolarizing noises for single-qubit and two-qubit gates, respectively, along with a 1% bit flip as readout noise. Table 8 shows the simulation results in noisy environments. We observed a notable decrease in the success rates of both DQAS and our method in noisy environments. Nonetheless, our method maintains an 18% advantage over DQAS in terms of success rate. In noisy environments, the average number of cuts achieved by our method is only 0.19 less than that in noise-free environments. This indicates that some circuits may not reach the theoretical maximum cut, but the cuts they achieve are very close to the theoretical maximum value. Strangely, DQAS yielded a higher number of cuts in the noisy environment by 0.08 compared to the noise-free environment. This could be due to the fact that in the noise-free environment, a significant proportion (26%) of MaxCut tasks were unable to reach the theoretical maximum cut by DQAS, whereas, in the presence of noise, a small number of MaxCut tasks might achieve better cuts.

Table 8 Simulation results of different QAS algorithms on QAOA in noisy environments
Full size table

6 Conclusion

In this paper, we proposed to directly produce optimal circuit structures for new VQA tasks by using a variational autoencoder trained on a variety of training tasks. Simulation results in variational quantum compiling demonstrate that the proposed algorithm can obtain quantum circuits with comparable performance compared to the DQAS algorithm while consuming just 2.6% of its running time. Additionally, we developed a meta-predictor to filter out candidate circuits with unsatisfying performances, resulting in a further 50% reduction in the total running time.

Our method trains a circuit generator through amortized meta-learning on multiple training tasks, requiring ground-truth sets. The ground-truth sets can be derived from benchmarks or historical tasks. Once a circuit generator is trained on multiple training tasks, it can be adapted to a variety of unseen tasks. The training of the meta-generator is a one-time process that can be executed offline, thereby mitigating the concern over the complexity involved in the collection of training tasks. The training tasks for the meta-training stage can be efficiently generated by training-free QAS algorithms [54], which do not require circuit training to assess circuit performance. We will explore the construction of training tasks using training-free QAS in our future work.