Robust implementation of generative modeling with parametrized quantum circuits

Abstract

Although the performance of hybrid quantum-classical algorithms is highly dependent on the selection of the classical optimizer and the circuit ansätze (Benedetti et al, npj Quantum Inf 5:45, 2019; Hamilton et al, 2018; Zhu et al, 2018), a robust and thorough assessment on-hardware of such features has been missing to date. From the optimizer perspective, the primary challenge lies in the solver’s stochastic nature, and their significant variance over the random initialization. Therefore, a robust comparison requires one to perform several training curves for each solver before one can reach conclusions about their typical performance. Since each of the training curves requires the execution of thousands of quantum circuits in the quantum computer, such a robust study remained a steep challenge for most hybrid platforms available today. Here, we leverage on Rigetti’s Quantum Cloud Services (QCS™) to overcome this implementation barrier, and we study the on-hardware performance of the data-driven quantum circuit learning (DDQCL) for three different state-of-the-art classical solvers, and on two-different circuit ansätze associated to different entangling connectivity graphs for the same task. Additionally, we assess the gains in performance from varying circuit depths. To evaluate the typical performance associated with each of these settings in this benchmark study, we use at least five independent runs of DDQCL towards the generation of quantum generative models capable of capturing the patterns of the canonical Bars and Stripes dataset. In this experimental benchmarking, the gradient-free optimization algorithms show an outstanding performance compared to the gradient-based solver. In particular, one of them had better performance when handling the unavoidable noisy objective function to be minimized under experimental conditions.

Appendices

Appendix A: DDQCL pipeline

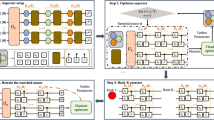
In this work, we implement a hybrid quantum-classical algorithm for unsupervised machine learning tasks introduced in (Benedetti et al. 2019) at Rigetti’s superconducting quantum computer (QPU). In the following, we present a short introduction of the approach, for a complete discussion see (Benedetti et al. 2019). The algorithm generates a probability distribution model for a given classical dataset ${\mathcal {X}} = \lbrace \boldsymbol {x}^{(1)}, \boldsymbol {x}^{(2)}, \cdots , \boldsymbol {x}^{(D)} \rbrace$ with distribution $P_{\mathcal {X}}$. Without lost of generality, the elements of ${\mathcal {X}}$ can be considered as N-dimensional binary vectors x⁽ⁱ⁾ ∈{0, 1}^N for i = 1,....,D, allowing a direct connection with the basis of an N-qubit quantum state, i.e., $\boldsymbol {x}^{(i)} \rightarrow | \boldsymbol {x}^{(i)} \rangle = | x_{1}^{(i)},...,x_{N}^{(i)} \rangle$ for i = 1,...,D. The goal is to prepare a quantum state $|\psi \rangle = {\sum }_{\boldsymbol {x} \in \{ 0,1 \}^{N} } \alpha _{\boldsymbol {x}} |\boldsymbol {x} \rangle$, with a probability distribution that mimics the dataset distribution, $|\langle \boldsymbol {x} | \psi \rangle |^{2} = |\alpha _{\boldsymbol {x}}|^{2} = P_{\mathcal {X}} (\boldsymbol {x})$ for x ∈{0, 1}^N.

The required quantum state |ψ〉 is prepared by tuning a PQC composed of single rotations and entangling gates with fixed depth and gate layout. In general, the circuit parameters of amount L can be written in a vector form 𝜃 = {𝜃₁,...,𝜃_L}, that prepares a state |ψ_𝜃〉 with distribution P_𝜃. The algorithm varies 𝜃 to get a minimal loss from P_𝜃 to $P_{\mathcal {X}}$. Here, we consider the Jensen-Shannon divergence (D_JS) to measure the loss, and determine how to update 𝜃 using a classical optimizer.

The D_JS divergence is a symmetrized and smoothed version of the Kullback-Leibler divergence (D_KL) (Weng 2019), defined as

$$ D_{\text{JS}}(P|Q) = \frac{1}{2} D_{\text{KL}}(P | M ) + \frac{1}{2} D_{\text{KL}}(Q | M ), $$

(A1)

where P and Q are distributions, and M = (P + Q)/2 their average. The Kullback-Leibler divergence is defined as

$$ \begin{array}{@{}rcl@{}} D_{\text{KL}}(X | M) &=& \underset{s \ \in \ \{ 0,1 \}^{N}}{\sum} X(s) \ln \left( X(s) \right )\\ &&-\underset{s \ \in \ \{ 0,1 \}^{N}}{\sum} X(s) \ln \left (M(s) \right), \end{array} $$

(A2)

for X ∈{P,Q}.

After the algorithm evaluates the cost from P_𝜃 to $P_{\mathcal {X}}$, it follows a quantum circuit parameters update in pursuit to a minimal cost. This procedure is done by an optimizer that runs on a classical processor unit (CPU). In summary, the algorithm chooses a random set of parameters 𝜃, evaluates the cost from P_𝜃 to the target $P_{\mathcal {X}}$ through the Jensen-Shannon divergence $D_{\text {JS}} (P_{\boldsymbol {\theta }} | P_{\mathcal {X}} )$, and updates 𝜃

minimizing the cost. This procedure is repeated several times (iterations) until a convergence criterion is met, for instance, a maximum number of iterations.

Appendix B: Experimental details

1.1 B.1 Quantum circuit model design

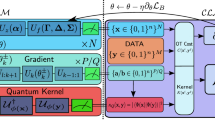
Since the quantum state probabilistic distribution does not depend on local quantum state phases, we chose a layout of the model circuit that prepares real amplitude quantum states. We consider the following two-qubit ansätze as the base to design N-qubit the circuit layout for DDQCL,

$$ \begin{array}{@{}rcl@{}} \mathcal{U}_{2}(\theta, \gamma, \beta) |00\rangle &=& R_{1}^{\beta} R_{0}^{\gamma} \text{CZ}_{01} R_{0}^{\theta} |00 \rangle \\ &=& \underset{s \in \{0,1\}^{2}}{\sum} \! \!\!\alpha_{s} |s\rangle \end{array} $$

(3)

therein $R_{k}^{\theta } = \exp [-i \theta {\sigma ^{y}_{k}} /2]$ is a local rotation around y-axis in the Bloch sphere on the k th qubit and CZ_kl the control phase shift gate between k th and l th qubits. The gate $\mathcal {U}_{2}$ defines a one-to-one map $[0, 2 \pi )^{3} \leftrightarrow S^{3}$, that ensures the preparation of any 2 qubit state with real probability amplitudes (Perdomo et al. 2021), i.e. α_s ∈IR for s ∈{0, 1}². For setups with more than 2 qubits, we use $\mathcal {U}_{2}$ to entangle different pairs of qubits depending on their connectivity, until getting a fully controlled entangled state. In this study, we consider four qubits with different connections (topologies) according to the Rigetti’s quantum computer architecture. We designed several circuits for line and star topologies using up to L = 16 local rotations and 6 CZ’s (see Fig. 3).

In silico simulations on noiseless qubits show that this circuit layout can learn a quantum model capable of successfully reproducing the target probability from the (2,2)BAS (see Appendix Appendix).

As pointed in the main text, one of the advantages of this circuit layout compared to the one considering arbitrary single-qubit rotations is the reduction in the number of parameters. On the other hand, it is important to note that having the additional parameters could in principle help the search since these open more paths in the Hilbert space, resulting in an increased number of states that could lead to a perfect $P_{\mathcal {X}}$ (see e.g., the discussion in the “Entanglement entropy of BAS(2,2)” section in the Supp. Material of Ref. (Benedetti et al. 2019)). This trade-off between flexibility in the quantum model and difficulty in optimization is beyond the scope of this work, and it would be an interesting research direction to explore.

1.2 B.2 Classical optimizers

For the experimental and numerical benchmarking study, we consider the following solvers and configurations.

• ZOOPT: The Zeroth-Order Optimization algorithm is a package that collects state-of-the-art zeroth-order optimization methods. The algorithm used by ZOOPT does not use the gradient of the objective function, it learns from samples of the search space. This method is convenient for optimizing cost functions that are not differentiable, with several local minima like the cost function we used in this work. Due to the stochastic nature of the cost function, we consider a value-suppression setting in the ZOOPT configuration. Additionally, we configured the initial population or initial number of evaluations as N_ini = 3L, with L as the number of parameters in the parametric quantum circuit.

• SVHC: This algorithm is the stochastic version of the ‘hill-climbing’ solver, with a variational searching size region. This algorithm is gradient-free, the criterion for new candidate solutions is based in samples of the search space. We consider an initial population N_ini = 3L, with L as the number of parameters in the quantum circuit.

• ADAM: This algorithm is an extension of classical stochastic gradient-descent algorithm, a combination of Adaptive Gradient Algorithm and Root Mean Square Propagation. Its performance depends on the derivative implementation of the objective function. We consider the setup used in Ref. (Hamilton et al. 2018), with learning rate α = 0.2, decay rates β₁ = 0.9, and β₂ = 0.999.

1.3 B.3 Improvement via readout correction

DDQCL is based on the probability distribution of the N qubit quantum state, which is in turn transformed into resulting bitstrings {0, 1}^N, denoted as shots in the main text. Unfortuantely, no device is 100% free of errors in this transformation from quantum state to bitstring output. Next, we describe a simple model to cope with this classical readout channel. Although there have been other procedures which are scalable (Kandala et al. 2017; Dumitrescu et al. 2018; Magnard et al. 2018), here we exploit our small number of qubits to make the least number of assumptions on the channel and perform an exponential number of experiments, which need to be done once to characterize the channel.

Table 2 Performance figures of merit from in silico simulations of the different HQC features explored in this work

The simple error readout correction implemented here consist of the measurement characterization of all the 2^N projectors π_x = |x〉〈x|, with x ∈{0, 1}⁴ for the (2,2)BAS realization here. Suppose you trivially prepare any of the 2⁴ states of the computational basis, e.g., x = 0010. In a noiseless scenario that measurement should yield a bitstring x = 0010 in the classical register for every single shot, allowing the computation of the P_x = 1.0, as expected from preparation. However, in the experiment the readouts correspond to different elements y ∈{0, 1}⁴ with a distribution p(y|x) due to assignment errors. In our procedure, we use a large number of readouts (set to 10,000 shots) to compute the distribution p(y|x), after trivial preparation of each x ∈{0, 1}⁴. Each of the p(y|x) is used as the x th column of the transition matrix M. Thus, any quantum state with population P_x is related with actual observed output distribution P_y as P_y = MP_x. To recover the original distribution from the quantum state, we invert the relation between P_x and P_y, i.e. P_x = M^− 1P_y. Before each batch of five of learning curves, we calculate the inverse transformation M^− 1 and apply this to the readout distribution; this defines a post-measurement process before the score and optimization steps.

To test the efficacy of this procedure, in Fig. 5, we present the training with the bare and the readout corrected training. The latter shows significant improvement with a minimal score of KL $\sim 0.13$ from $\sim 1.0$ obtained using bare readouts. Therefore, we adopted the readout correction for all the experiments reported in the main text.

Fig. 5

Comparison of DDQCL with and without readout correction. Full learning curve is shown (left) with and without readout correction (blue and green line, respectively). Without error correction, the minimal value reached for the KL divergence is $\sim 1.0$, which is closer to a random distribution, and far from the target one (see histograms on the upper right). On the other hand, the training curve with readout correction reached a value of $KL \sim 0.13$, which is a significant improvement in the DDQCL

Fig. 6

DDQCL simulations in silico, and under the assumption of noiseless qubits, but taking into account the stochasticity from finite readouts. In this simulations we used 3000 shots per circuit

1.4 B.4 QPU specifics

In this work, we had access to the 16Q Aspen-1 quantum chip. This chip has 0.05μ s and 0.15μ s of coherence time for one and two qubit gates, respectively. With a T₁ = 28.71μ and T₂ = 20.34μ s, the quantum chip can support the quantum operations defined this work.

Appendix C: In silico simulations

1.1 C.1 Bootstrap** details

We resample the experimental outcome of the five independent DDQCL into 10,000 datasets of five with replacement and compute the median D_JS for each. From the distribution of 10,000 medians, we computed the median and obtained error bars from the 5th and 95th percentiles as the lower and upper limits, respectively, accounting for a 90% confidence interval.