SpringerLink
Log in

Riemann–Hilbert approach and \(N\)-soliton solutions of the generalized mixed nonlinear Schrödinger equation with nonzero boundary conditions

  • Research Articles
  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

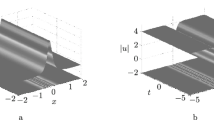
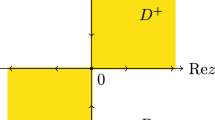
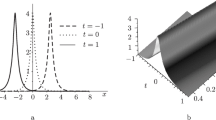
We apply the inverse scattering transformation to the generalized mixed nonlinear Schrödinger equation with nonzero boundary condition at infinity. The scattering theories are investigated. In the direct problem, we analyze the analyticity, symmetries, and asymptotic behaviors of the Jost solutions and the scattering matrix, and the properties of the discrete spectrum. In the inverse problem, an appropriate Riemann–Hilbert problem is formulated. By solving the problem, we obtain the reconstruction formula, the trace formula, and the “theta” condition. In the reflectionless case, a complicated integral factor is derived, which is a key ingredient of the explicit expression for \(N\)-soliton solutions. Using the \(N\)-soliton formula, we discuss the abundant dynamical features of the solution and its phases at different parameter values.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.

Similar content being viewed by others

References

  1. A. Hasegawa and F. Tappert, “Transmission of stationary nonlinear optical physics in dispersive dielectric fibers. I. Anomalous dispersion,” Appl. Phys. Lett., 23, 142–144 (1972).

    Article  ADS  Google Scholar 

  2. G. P. Agrawal, Nonlinear Fiber Optics, Academic Press, New York (2007).

    MATH  Google Scholar 

  3. D. J. Benney and A. C. Newell, “Propagation of nonlinear wave envelopes,” J. Math. Phys., 46, 133–139 (1967).

    Article  MathSciNet  MATH  Google Scholar 

  4. F. Dalfovo, S. Giorgini, L. P. Pitaevskii, and S. Stringari, “Theory of Bose–Einstein condensation in trapped gases,” Rev. Modern Phys., 71, 463–512 (1999); ar**v: cond-mat/9806038.

    Article  ADS  Google Scholar 

  5. R. Hirota, The Direct Method in Soliton Theory (Cambridge Tracts in Mathematics, Vol. 155), Cambridge Univ. Press, Cambridge (2004).

    Book  MATH  Google Scholar 

  6. Y. Li, X. Gu, and M. Zou, “Three kinds of Darboux transformation for the evolution equation which connect with A.K.N.S. eigenvalue problem,” Acta Math. Sin. (N. S.), 3, 143–151 (1987).

    Article  MathSciNet  MATH  Google Scholar 

  7. S. P. Novikov, S. V. Manakov, L. P. Pitaevskii, and V. E. Zakharov, Theory of Solitons. The Inverse Scattering Methods, Consultants Bureau, New York (1984).

    MATH  Google Scholar 

  8. M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering, Cambridge Univ. Press, Cambridge (1991).

    Book  MATH  Google Scholar 

  9. V. E. Zakharov and A. B. Shabat, “Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media,” Sov. Phys. JETP, 34, 62–69 (1972).

    ADS  MathSciNet  Google Scholar 

  10. Y.-C. Ma and M. J. Ablowitz, “The periodic cubic Schrödinger equation,” Stud. Appl. Math., 65, 113–158 (1981).

    Article  MathSciNet  MATH  Google Scholar 

  11. D. H. Peregrine, “Water waves, nonlinear Schrödinger equations and their solutions,” J. Austral. Math. Soc. Ser. B, 25, 16–43 (1983).

    Article  MathSciNet  MATH  Google Scholar 

  12. L. D. Faddeev and L. A. Takhtajan, Hamiltonian Methods in the Theory of Solitons, Springer, Berlin (1987).

    Book  MATH  Google Scholar 

  13. T. Brabec and F. Krausz, “Intense few-cycle laser fields: Frontiers of nonlinear optics,” Rev. Modern Phys., 72, 545–591 (2000).

    Article  ADS  Google Scholar 

  14. F. Krausz and M. Ivanov, “Attosecond physics,” Rev. Modern Phys., 81, 163–234 (2009).

    Article  ADS  Google Scholar 

  15. R. S. Johnson, “On the modulation of water waves in the neighbourhood of \(kh\approx 1.363\),” Proc. Roy. Soc. London Ser. A, 357, 131–141 (1977).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Y. Kodama, “Optical solitons in a monomode fiber,” J. Stat. Phys., 39, 597–614 (1985).

    Article  ADS  MathSciNet  Google Scholar 

  17. P. A. Clarkson and J. A. Tuszynski, “Exact solutions of the multidimensional derivative nonlinear Schrödinger equation for many-body systems of criticality,” J. Phys. A: Math. Gen., 23, 4269–4288 (1990).

    Article  ADS  MATH  Google Scholar 

  18. A. Rogister, “Parallel propagation of nonlinear low-frequency waves in high-\(\beta\) plasma,” Phys. Fluids, 14, 2733–2739 (1971).

    Article  ADS  Google Scholar 

  19. D. J. Kaup and A. C. Newell, “An exact solution for a derivative nonlinear Schrödinger equation,” J. Math. Phys., 19, 798–801 (1978).

    Article  ADS  MATH  Google Scholar 

  20. E. Mjolhus, “On the modulational instability of hydromagnetic waves parallel to the magnetic field,” J. Plasma Phys., 16, 321–334 (1976).

    Article  ADS  Google Scholar 

  21. N. Tzoar and M. Jain, “Self-phase modulation in long-geometry optical waveguides,” Phys. Rev. A, 23, 1266–1270 (1981).

    Article  ADS  Google Scholar 

  22. D. Anderson and M. Lisak, “Nonlinear asymmetric self-phase modulation and self-steepening of pulses in long optical waveguides,” Phys. Rev. A, 27, 1393–1398 (1983).

    Article  ADS  Google Scholar 

  23. H. H. Chen, Y. C. Lee, and C. S. Liu, “Integrability of nonlinear Hamiltonian systems by inverse scattering method,” Phys. Scr., 20, 490–492 (1979).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. V. S. Gerdjikov and M. I. Ivanov, “A quadratic pencil of general type and nonlinear evolution equations. II. Hierarchies of Hamiltonian structures,” Bulg. J. Phys., 10, 130–143 (1983).

    MathSciNet  Google Scholar 

  25. J. Moses, B. A. Malomed, and F. W. Wise, “Self-steepening of ultrashort optical pulses without self-phase-modulation,” Phys. Rev. A, 76, 021802, 4 pp. (2007).

    Article  ADS  Google Scholar 

  26. A. Kundu, “Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations,” J. Math. Phys., 25, 3433–3438 (1984).

    Article  ADS  MathSciNet  Google Scholar 

  27. Y. J. **ang, X. Y. Dai, S. C. Wen, J. Guo, and D. Y. Fan, “Controllable Raman soliton self-frequency shift in nonlinear metamaterials,” Phys. Rev. A, 84, 033815, 7 pp. (2011).

    Article  ADS  Google Scholar 

  28. A. Choudhuri and K. Porsezian, “Dark-in-the-Bright solitary wave solution of higher-order nonlinear Schrödinger equation with non-Kerr terms,” Opt. Commun., 285, 364–367 (2012).

    Article  ADS  Google Scholar 

  29. P. A. Clarkson and C. M. Cosgrove, “Painlevé analysis of the non-linear Schrödinger family of equations,” J. Phys. A: Math. Gen., 20, 2003–2024 (1987).

    Article  ADS  MATH  Google Scholar 

  30. S. Kakei, N. Sasa, and J. Satsuma, “Bilinearization of a generalized derivative nonlinear Schrödinger equation,” J. Phys. Soc. Japan, 64, 1519–1523 (1995); ar**v: solv-int/9501005.

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. X. Lü, “Soliton behavior for a generalized mixed nonlinear Schrödinger model with \(N\)-fold Darboux transformation,” Chaos, 23, 033137, 8 pp. (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. D. Qiu and Q. P. Liu, “Darboux transformation of the generalized mixed nonlinear Schrödinger equation revisited,” Chaos, 30, 123111, 17 pp. (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. X. Lü and M. Peng, “Systematic construction of infinitely many conservation laws for certain nonlinear evolution equations in mathematical physics,” Commun. Nonlinear Sci. Numer. Simulat., 18, 2304–2312 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. L. Wang, D.-Y. Jiang, F.-H. Qi, Y.-Y. Shi, and Y.-C. Zhao, “Dynamics of the higher-order rogue waves for a generalized mixed nonlinear Schrödinger model,” Commun. Nonlinear Sci. Numer. Simulat., 42, 502–519 (2017).

    Article  ADS  MATH  Google Scholar 

  35. B. Yang, J. Chen, and J. Yang, “Rogue waves in the generalized derivative nonlinear Schrödinger equations,” J. Nonlinear Sci., 30, 3027–3056 (2020); ar**v: 1912.05589.

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. J. K. Yang, Nonlinear Waves in Integrable and Nonintegrable Systems (Mathematical Modeling and Computation, Vol. 16), SIAM, Philadelphia, PA (2010).

    Book  MATH  Google Scholar 

  37. P. Deift and X. Zhou, “A steepest descent method for oscillatory Riemann–Hilbert problems,” Ann. Math., 137, 295–368 (1993).

    Article  MathSciNet  MATH  Google Scholar 

  38. G. Biondini and G. Kovăcič, “Inverse scattering transform for the focusing nonlinear Schrödinger equation with nonzero boundary conditions,” J. Math. Phys., 55, 031506, 22 pp. (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. M. Pichler and G. Biondini, “On the focusing non-linear Schrödinger equation with non-zero boundary conditions and double poles,” IMA J. Appl. Math., 82, 131–151 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  40. G. Biondini and D. K. Kraus, “Inverse scattering transform for the defocusing Manakov system with nonzero boundary conditions,” SIAM J. Math. Anal., 47, 706–757 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  41. B. Prinari, M. J. Ablowitz, and G. Biondini, “Inverse scattering transform for the vector nonlinear Schrödinger equation with nonvanishing boundary conditions,” J. Math. Phys., 47, 063508, 33 pp. (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. G. Biondini, D. K. Kraus, and B. Prinari, “The three-component defocusing nonlinear Schrödinger equation with nonzero boundary conditions,” Commun. Math. Phys., 348, 475–533 (2016); ar**v: 1511.02885.

    Article  ADS  MATH  Google Scholar 

  43. G. Zhang and Z. Yan, “The derivative nonlinear Schrödinger equation with zero/nonzero boundary conditions: Inverse scattering transforms and \(N\)-double-pole solutions,” J. Nonlinear Sci., 30, 3089–3127 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  44. Z. Zhang and E. Fan, “Inverse scattering transform for the Gerdjikov-Ivanov equation with nonzero boundary conditions,” Z. Angew. Math. Phys., 71, 149, 28 pp. (2020).

    Article  MathSciNet  MATH  Google Scholar 

  45. Y. Yang and E. Fan, “Riemann–Hilbert approach to the modified nonlinear Schrödinger equation with non-vanishing asymptotic boundary conditions,” ar**v: 1910.07720.

  46. L.-L. Wen and E.-G. Fan, “The Riemann–Hilbert approach to focusing Kundu–Eckhaus equation with non-zero boundary conditions,” Modern Phys. Lett. B, 34, 2050332, 20 pp. (2020); ar**v: 1910.08921.

    Article  ADS  MathSciNet  Google Scholar 

  47. N. Guo and J. Xu, “Inverse scattering transform for the Kundu–Eckhaus equation with nonzero boundary conditions,” ar**v: 1912.11424.

  48. N. Guo, J. Xu, L. Wen, and E. Fan, “Rogue wave and multi-pole solutions for the focusing Kundu–Eckhaus equation with nonzero background via Riemann–Hilbert problem method,” Nonlinear Dyn., 103, 1851–1868 (2021).

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11871471 and 11931017), the Yue Qi Outstanding Scholar Project, China University of Mining and Technology, Bei**g (Grant No. 00-800015Z1177).

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Science, China University of Mining and Technology, Bei**g, China

    DeQin Qiu & Cong Lv

Authors
  1. DeQin Qiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cong Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to DeQin Qiu.

Ethics declarations

The authors declare no conflicts of interest.

Additional information

Translated from Teoreticheskaya i Matematicheskaya Fizika, 2021, Vol. 209, pp. 274–304 https://doi.org/10.4213/tmf10067.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiu, D., Lv, C. Riemann–Hilbert approach and \(N\)-soliton solutions of the generalized mixed nonlinear Schrödinger equation with nonzero boundary conditions. Theor Math Phys 209, 1552–1578 (2021). https://doi.org/10.1134/S0040577921110052

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577921110052

Keywords

Search

Navigation