Generalized Diffusion Characteristics of Calcium Model with Concentration and Memory of Cells: A Spatiotemporal Approach

Abstract

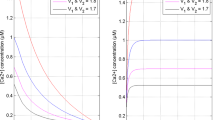
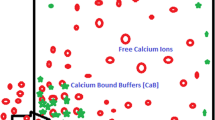
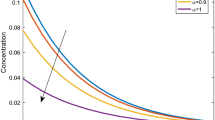
The anomalous diffusion gives a more concise description of the biophysical process. One of the indispensable processes in the nervous system is the diffusion of free calcium ($\hbox {Ca}^{2+}$) in nerve cells. An alteration/dysfunction of $\hbox {Ca}^{2+}$ leads to cell death and consequently manifests the early symptoms of many neurological disorders. In the context of this, we have presented a two-dimensional fractional-order reaction–diffusion model to develop a control mechanism of $\hbox {Ca}^{2+}$ dynamics. We have used the integral transform technique of arbitrary order to find the solution of the proposed $\hbox {Ca}^{2+}$ diffusion model. Due to the lack of smoothness of the solution, we have presented different schemes to obtain the closed-form solution. Finally, we have simulated the results in MATLAB software to show the diffusion characteristics on the $\hbox {Ca}^{2+}$ model and exhibit the control strategy to optimize calcium concentration. Furthermore, the obtained results are interpreted with the physiology of Parkinson’s. We observed that when space derivative moved from integer to fractional-order and the time derivative moved from fractional to integer-order we get an optimum control on $\hbox {Ca}^{2+}$ diffusion due to the intermediate memory and generalized diffusion characteristics of cells. Thus, we conclude that the generalized diffusion characteristics and memory of cells are enhanced the control strategy on the $\hbox {Ca}^{2+}$ diffusion model.