SpringerLink
Log in

Dynamics of a vibro-impact system by the global analysis method in parameter-state space

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

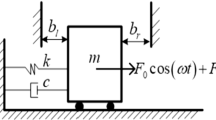
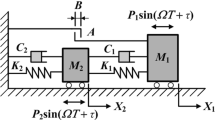
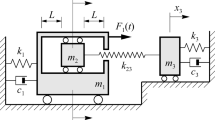
The global analysis method in parameter-state space for achieving both the distribution and the transition rule of periodic motions and the distribution rule of the multiple motions coexistence of the vibro-impact system is developed. A nonlinear dynamic model in a system of vibro-impact with asymmetric clearances is researched by the new method. Three grazing motions and relevant conditions have been discussed. The distribution and the transition rule of periodic motions are analyzed. The influence of the grazing and saddle-node bifurcation during the change in the left and the right gaps are demonstrated. The distribution of subharmonic motions is illustrated. The coexistence of multiple motions which exist at the junction of periodic motions within the motion-sensitive areas is researched by the global analysis method in parameter-state space, and the distributions of periodic motions and the multiple motions coexistence are illustrated. The transition of the multiple motions coexistence with the guide of the global distribution of the motions is further analyzed by the evolution of the attractors and the corresponding attracting domains. The results contribute a lot to the study of the transition and the control of the motions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (France)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Shaw, S.W., Holmes, P.: Periodically forced linear oscillator with impacts: chaos and long-period motions. Phys. Rev. Lett. 51(8), 623–626 (1983)

    Article  MathSciNet  Google Scholar 

  2. Thompson, J.M.T., Ghaffari, R.: Chaos after period-doubling bifurcations in the resonance of an impact oscillator. Phys. Lett. A 91(1), 5–8 (1982)

    Article  MathSciNet  Google Scholar 

  3. Janin, O., Lamarque, C.H.: Stability of singular periodic motions in a vibro-impact oscillator. Nonlinear Dyn. 28(3), 231–241 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  4. Li, Q.H., Lu, Q.S.: Coexisting periodic orbits in vibro-impacting dynamical systems. Appl. Math. Mech. 24(3), 234–244 (2003)

    MathSciNet  MATH  Google Scholar 

  5. Ding, W., Li, G., Luo, G., et al.: Torus T-2 and its locking, doubling, chaos of a vibro-impact system. J. Frankl. Inst. 349(1), 337–348 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  6. Yue, Y., **e, J., Gao, X.: Determining Lyapunov spectrum and Lyapunov dimension based on the Poincaré map in a vibro-impact system. Nonlinear Dyn. 69(3), 743–753 (2012)

    Article  MATH  Google Scholar 

  7. Li, G., Ding, W., Wu, S.: Global behavior of vibro-impact system with multiple non-smooth mechanical Factors. J. Comput. Nonlinear Dyn. 12(6), 061004-1–061004-11 (2017)

    Google Scholar 

  8. Li, G., Ding, W.: Global Behavior of a vibro-impact system with asymmetric clearances. J. Sound Vib. 423, 180–194 (2018)

    Article  Google Scholar 

  9. **ao-Juan, W., Ning-Zhou, L., Wang-Cai, D., et al.: Model-free chaos control based on AHGSA for a vibro-impact system. Nonlinear Dyn. 94, 845–855 (2018)

    Article  Google Scholar 

  10. Czolczynski, K., Kapitaniak, T.: On the existence of a stable periodic solution of an impacting oscillator with two fenders. Int. J. Bifurc. Chaos 14(9), 3115–3134 (2004)

    Article  MATH  Google Scholar 

  11. Nordmark, A.B.: Non-periodic motion caused by grazing incidence in an impact oscillator. J. Sound Vib. 145(2), 279–297 (1991)

    Article  Google Scholar 

  12. Whiston, G.S.: Singularities in vibro-impact dynamics. J. Sound Vib. 152(3), 427–460 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chin, W., Ott, E., Nusse, H.E., et al.: Universal behavior of impact oscillators near grazing incidence. Phys. Lett. A 201(2–3), 197–204 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lamba, H., Budd, C.J.: Scaling of Lyapunov exponents at non-smooth bifurcations. Phys. Rev. E. 50(1), 84–90 (1994)

    Article  MathSciNet  Google Scholar 

  15. Virgin, L.N., Begley, C.J.: Grazing bifurcations and basins of attraction in an impact-friction oscillator. Phys. D Nonlinear Phenom. 130(1–2), 43–57 (1999)

    Article  MATH  Google Scholar 

  16. Pavlovskaia, E., Ing, J., Wiercigroch, M., et al.: Complex dynamics of bilinear oscillator close to grazing. Int. J. Bifurc. Chaos. 20(11), 3801–3817 (2010)

    Article  MathSciNet  Google Scholar 

  17. Shan, Y., **chen, J., Shuning, D., et al.: Neimark–Sacker bifurcations near degenerate grazing point in a two degree-of-freedom impact oscillator. J. Comput. Nonlinear Dyn. 13(6), 111007-1–111007-8 (2018)

    Google Scholar 

  18. Chillingworth, D.R.J.: Discontinuity geometry for an impact oscillator. Dyn. Syst. 17(4), 389–420 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  19. Humphries, N., Piiroinen, P.T.: A discontinuity-geometry view of the relationship between saddle-node and grazing bifurcations. Phy. D 241(22), 1911–1918 (2012)

    Article  MathSciNet  Google Scholar 

  20. Jiang, H., Wiercigroch, M.: Geometrical insight into non-smooth bifurcations of a soft impact oscillator. J. Appl. Math. 81(4), 662–678 (2016)

    MathSciNet  MATH  Google Scholar 

  21. Luo, A.C.J., Chen, L.D.: Arbitrary periodic motions and grazing switching of a forced piecewise-linear, impacting oscillator. ASME J. Vib. Acoust. 129, 276–284 (2007)

    Article  Google Scholar 

  22. Wagg, D.J.: Periodic sticking motion in a two-degree-freedom impact oscillator. Int. J. Bifurc. Chaos 40(8), 1076–1087 (2005)

    MATH  Google Scholar 

  23. Nordmark, A.B., Piiroinen, P.T.: Simulation and stability analysis of impacting systems with complete chattering. Nonlinear Dyn. 58(1–2), 85–106 (2009)

    Article  MATH  Google Scholar 

  24. Ma, Y., Agarwal, M., Banerjee, S.: Border collision bifurcations in a soft impact system. Phys. Lett. A 354(4), 281–287 (2006)

    Article  Google Scholar 

  25. Gritli, Hassène, Belghith, S.: Diversity in the nonlinear dynamic behavior of a one-degree-of-freedom impact mechanical oscillator under OGY-based state-feedback control law: order, chaos and exhibition of the border-collision bifurcation. Mech. Mach. Theory 124, 1–41 (2018)

    Article  Google Scholar 

  26. Du, Z., Zhang, W.: Melnikov method for homoclinic bifurcation in nonlinear impact oscillators. Comput. Math. Appl. 50(3–4), 445–458 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  27. Xu, W., Feng, J., Rong, H.: Melnikov’s method for a general nonlinear vibro-impact oscillator. Nonlinear Anal. 71(1–2), 418–426 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  28. Hsu, C.S., Guttalu, R.S.: An unraveling algorithm for global analysis of dynamical systems: an application of cell-to-cell map**s. J. Appl. Mech. 47(4), 940–948 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  29. Hsu, C.S.: A generalized theory of cell-to-cell map** for nonlinear dynamical systems. ASME J. Appl. Mech. 48(3), 634–642 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  30. Hsu, C.S.: Global analysis by cell map**. Int. J. Bifurc. Chaos 2(4), 727–771 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  31. Zufiria, P.J., Guttalu, R.S.: The adjoining cell map** and its recursive unraveling, part I: description of adaptive and recursive algorithms. Nonlinear Dyn. 4(3), 207–226 (1993)

    Google Scholar 

  32. Guttalu, R.S., Zufiria, P.J.: The adjoining cell map** and its recursive unraveling, part II: application toselected problems. Nonlinear Dyn. 4(4), 309–336 (1993)

    Article  Google Scholar 

  33. Guder, R., Dellnitz, M., Kreuzer, E.: An adaptive method for the approximation of the generalized cell map**. Chaos Solitons Fractals 8(4), 525–534 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  34. ** method for global analysis of high-dimensional nonlinear dynamical systems. J. Appl. Mech. 82(11), 111010-1–111010-12 (2015)

    Article  Google Scholar 

  35. Liu, X., Hong, L., Jiang, J., et al.: Global dynamics of fractional-order systems with an extended generalized cell map** method. Nonlinear Dyn. 83(3), 1419–1428 (2016)

    Article  MathSciNet  Google Scholar 

  36. Gao, X.J., Li, Y.H., Yue, Y., et al.: Symmetric/asymmetric bifurcation behaviours of a bogie system. J. Sound Vib. 332(4), 936–951 (2013)

    Article  Google Scholar 

  37. Liu, Y., Pavlovskaia, E., Wiercigroch, M., et al.: Forward and backward motion control of a vibro-impact capsule system. Int. J. Nonlinear Mech. 70, 30–46 (2015)

    Article  Google Scholar 

  38. Luo, A.C.J., O’Connor, D.: Periodic motions and chaos with impacting chatter and stick in a gear transmission system. Int. J. Bifurc. Chaos 19(6), 0902385 (2014)

    MathSciNet  Google Scholar 

  39. Huang, Z.L., Liu, Z.H., Zhu, W.Q.: Stationary response of multi-degree-of-freedom vibro-impact systems under white noise excitations. J. Sound Vib. 275(1), 223–40 (2004)

    Article  Google Scholar 

  40. **e, J.: A mathematical model for the impact hammer and it’s global bifurcations. Acta Mech. Sin. 13(4), 456–463 (1997)

    MathSciNet  Google Scholar 

  41. Ibrahim, R.A.: Vibro-Impact Dynamics: Modeling, Map** and Applications. Lecture Notes in Applied and Computational Mechanics, vol. 43. Springer, Berlin (2009)

    Book  Google Scholar 

  42. Awrejcewicz, J., Lamarque, C.H.: Bifurcation and Chaos in Nonsmooth Mechanical Systems, vol. 45. World Scientific, Singapore (2003)

    Book  MATH  Google Scholar 

  43. Luo, A.C.J., Yu, G.: Vibro-Impact Dynamics. Wiley, London (2013)

    Book  MATH  Google Scholar 

  44. Leine, R.I., Campen, D.H.V., Vrande, B.L.V.D.: Bifurcations in nonlinear discontinuous systems. Nonlinear Dyn. 23(2), 105–164 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  45. Leine, R.I., Nijmeijer, H.: Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Lecture Notes in Applied and Computational Mechanics, vol. 18. Springer, Berlin (2004)

    Book  MATH  Google Scholar 

  46. Hsu, C.S.: Cell-to-Cell Map**: A Method of Global Analysis for Nonlinear Systems. Springer, Berlin (1987)

    Book  MATH  Google Scholar 

  47. Sun, J.Q., ** Methods Algorithmic Approaches and Applications. Springer, Berlin (2019)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

We acknowledge the editors and the anonymous reviewers for insightful suggestions on this work. This work is supported by the National Natural Science Foundation of China (11462011, 11732014), the Gansu Provincial Natural Science Foundation of China (17JR5RA098).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou, 730070, People’s Republic of China

    Guofang Li & Wangcai Ding

  2. International Cooperation and Exchange Office, Lanzhou Jiaotong University, Lanzhou, 730070, People’s Republic of China

    Jie Sun

Authors
  1. Guofang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jie Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wangcai Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wangcai Ding.

Ethics declarations

Conflict of interest

We declare that we have no conflict of interest concerning the publication of this manuscript and the paper is in compliance with ethical standards.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, G., Sun, J. & Ding, W. Dynamics of a vibro-impact system by the global analysis method in parameter-state space. Nonlinear Dyn 97, 541–557 (2019). https://doi.org/10.1007/s11071-019-04996-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04996-6

Keywords

Search

Navigation