SpringerLink
Log in

Diversity and transition characteristics of sticking and non-sticking periodic impact motions of periodically forced impact systems with large dissipation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

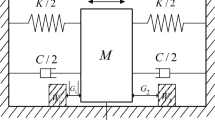
A forced vibration system with dual bodies and an endstop is considered in this paper. A large energy loss is considered as one of the mass blocks of the system hits the endstop, and the impact associated with the large energy loss is first assumed to be completely plastic. The plastic impact may bring about the occurrence of the sticking phase, which is equivalent to a change in the structure of the forced vibration system at a certain stage after the impact. The incidence relation between dynamical characteristics and model parameters is studied through the multi-target and multi-parameter collaborative simulation analysis for determining the reasonable matching range of parameters. Pattern types, occurrence regions, distribution regularities and bifurcation characteristics of periodic and subharmonic impact vibrations are presented on a series of parameter planes. The key features of Poincaré map**, associated with the plastic impacts, are primarily manifested in piecewise continuity caused by sliding bifurcation and grazing discontinuity induced by grazing bifurcation. Integrative effects of these two nonstandard bifurcations can bring about some abnormal transitions to occur. The large dissipation case associated with small collision recovery coefficient is briefly analyzed, and the induced mechanism of chatter-sticking motion and the incidence relation between the sticking characteristics and the restitution coefficient R are discussed. The nonstandard dynamic characteristics associated with the plastic impacts are further demonstrated by dynamic mechanical behaviors of two practical impact machines applied in engineering.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  1. Shaw, S.W., Holmes, P.J.: A periodically forced piecewise linear oscillator. J. Sound Vib. 90(1), 129–155 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  2. Peterka, F.: Bifurcations and transition phenomena in an impact oscillator. Sour. Chaos Solitons Fract 7(10), 1635 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  3. Aidanpää, J.O., Gupta, B.R.: Periodic and chaotic behaviour of a threshold-limited two-degree-of-freedom system. J. Sound Vib. 165(2), 305–327 (1993)

    Article  MATH  Google Scholar 

  4. Xu, D., Bishop, S.R.: The use of control to eliminate subharmonic and chaotic impacting motions of a driven beam. J. Sound Vib. 205(2), 223–234 (1997)

    Article  Google Scholar 

  5. Kozol, J.E., Brach, R.M.: Two-dimensional vibratory impact and chaos. J. Sound Vib. 148, 319–327 (1991)

    Article  Google Scholar 

  6. Knudsen, J., Massih, A.R.: Dynamic stability of weakly damped oscillators with elastic impacts and wear. J. Sound Vib. 263(1), 175–204 (2003)

    Article  Google Scholar 

  7. Natsiavas, S.: Dynamics of multiple-degree-of-freedom oscillators with colliding components. J. Sound Vib. 165, 439–453 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  8. Pavlovskaia, E., Wiercigroch, M., Grebogi, C.: Two-dimensional map for impact oscillator with drift. Phys. Rev. E 70(3), 036201 (2004)

    Article  Google Scholar 

  9. Leine, R.I., van Campen, D.H.: Bifurcation phenomena in non-smooth dynamical systems. Eur. J. Mech. A/Solids 25(4), 595–616 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Czolczynski, K., Okolewski, A., Blazejczyk-Oolewskaa, B.: Lyapunov exponents in discrete modelling of a cantilever beam impacting on a moving base. Int. J. Non Linear Mech. 88, 74–84 (2017)

    Article  Google Scholar 

  11. Ibrahim, R.A.: Vibro-Impact Dynamics. Springer, Berlin (2009)

    Book  MATH  Google Scholar 

  12. Nordmark, A.B.: Non-periodic motion caused by grazing incidence in an impact oscillator. J. Sound Vib. 145(2), 279–297 (1991)

    Article  Google Scholar 

  13. Whiston, G.S.: Singularities in vibro-impact dynamics. J. Sound Vib. 152(3), 427–460 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hu, H.Y.: Detection of grazing orbits and incident bifurcations of a forced continuous, piecewise-linear oscillator. J. Sound Vib. 187(3), 485–493 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  15. Foale, S., Bishop, S.R.: Dynamical complexities of forced impacting systems. Philos. Trans. R. Soc. Lond. 338(A), 547–556 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ivanov, A.P.: Stabilization of an impact oscillator near grazing incidence owing to resonance. J. Sound Vib. 162(3), 562–565 (1993)

    Article  MATH  Google Scholar 

  17. de Weger, J., van de Water, W., Molenaar, J.: Grazing impact oscillations. Phys. Rev. E 62(2B), 2030–2041 (2000)

    Article  Google Scholar 

  18. di Bernardo, M., Nordmark, A., Olivar, G.: Discontinuity-induced bifurcations of equilibria in piecewise-smooth and impacting dynamical systems. Physica D 237, 119–36 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. di Bernardo, M., Budd, C.J., Champneys, A.R.: Grazing and border-collision in piecewise-smooth systems: a unified analytical framework. Phys. Rev. Lett. 86(12), 2553–2556 (2001)

    Article  Google Scholar 

  20. Colombo, A., Dercole, F.: Discontinuity-induced bifurcations of nonhyperbolic cycles in non-smooth systems. SIAM J. Appl. Dyn. Syst. 9(1), 62–83 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Luo, A.C.J., Chen, L.: Periodic motions and grazing in a harmonically forced, piecewise, linear oscillator with impacts. Chaos Solitons Fract. 24(2), 567–578 (2005)

    Article  MATH  Google Scholar 

  22. Thota, P., Dankowicz, H.: Continuous and discontinuous grazing bifurcations in impacting oscillators. Physica D 214, 187–197 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ma, Y., Ing, J., Banerjee, S., Wiercigroch, M., Pavlovskaia, E.: The nature of the normal form map for soft impacting systems. Int. J. Non Linear Mech. 43(6), 504–513 (2008)

    Article  Google Scholar 

  24. Mason, J.F., Piiroinen, P.T.: Interactions between global and grazing bifurcations in an impacting System. Chaos 21, 013113 (2011)

    Article  MathSciNet  Google Scholar 

  25. Mason, J.F., Piiroinen, P.T.: Saddle-point solutions and grazing bifurcations in an impacting system. Chaos 22, 013106 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Chillingworth, D.: Dynamics of an impact oscillator near a degenerate graze. Nonlinearity 23(11), 2723–2748 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dankowicz, H., Katzenbach, M.: Discontinuity-induced bifurcations in models of mechanical contact, capillary adhesion, and cell division: a common framework. Physica D 241(22), 1869–1881 (2012)

    Article  MathSciNet  Google Scholar 

  28. Jiang, H., Chong, A.S.E., Uedab, Y., Wiercigroch, M.: Grazing-induced bifurcations in impact oscillators with elastic and rigid constraints. Int. J. Mech. Sci. 127, 204–214 (2017)

    Article  Google Scholar 

  29. Dankowicz, H., Zhao, X.: Local analysis of co-dimension-one and co-dimension-two grazing bifurcations in impact microactuators. Physica D 202(3–4), 238–257 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Humphries, N., Piiroinen, P.T.: A discontinuity-geometry view of the relationship between saddle-node and grazing bifurcations. Physica D 241(22), 1911–1918 (2012)

    Article  MathSciNet  Google Scholar 

  31. Kryzhevich, S., Wiercigroch, M.: Topology of vibro-impact systems in the neighborhood of grazing. Physica D 241(22), 1919–1931 (2012)

    Article  MathSciNet  Google Scholar 

  32. Mason, J.F., Humphries, N., Piiroinen, P.T.: Numerical analysis of codimension-one, -two and -three bifurcations in a periodically- forced impact oscillator with two discontinuity surfaces. Math. Comput. Simul. 95, 98–110 (2014)

    Article  MathSciNet  Google Scholar 

  33. Budd, C.J., Dux, F.: Chattering and related behaviour in impact oscillators. Philos. Trans. R. Soc. Lond. A 347, 365–389 (1994)

    Article  MATH  Google Scholar 

  34. Ema, S., Marui, E.: Suppression of chatter vibration of boring tools using impact dampers. Int. J. Mach. Tools Manuf. 40(8), 1141–1156 (2000)

    Article  Google Scholar 

  35. Toulemonde, C., Gontier, C.: Sticking motions of impact oscillators. Eur. J. Mech. A/Solids 17(2), 339–366 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  36. Wagg, D.J.: Multiple non-smooth events in multi-degree-of-freedom vibro-impact systems. Nonlinear Dyn. 43, 137–148 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  37. Nordmark, A.B., Piiroinen, P.T.: Simulation and stability analysis of impacting systems with complete chattering. Nonlinear Dyn. 58, 85–106 (2009)

    Article  MATH  Google Scholar 

  38. de Souza, S.L.T., Iberê, L.: Caldas, Basins of attraction and transient chaos in a gear-rattling model. J. Vib. Control 7(6), 849–862 (2001)

    Article  MATH  Google Scholar 

  39. Luo, A.C.J., O’Connor, D.: Mechanism of impacting chatter with stick in a gear transmission system. Int. J. Bifurc. Chaos 19(6), 2093–2105 (2009)

    Article  MathSciNet  Google Scholar 

  40. Mason, J.F., Piiroinen, P.T., Eddie Wilson, R.: Basins of attraction in nonsmooth models of gear rattle. Int. J. Bifurc. Chaos 19(1), 203–224 (2009)

    Article  MathSciNet  Google Scholar 

  41. Hös, C., Champneys, A.R.: Grazing bifurcations and chatter in a pressure relief valve model. Physica D 241, 2068–2076 (2012)

    Article  MathSciNet  Google Scholar 

  42. **, D., Haiyan, H.: An experimental study on possible types of vibro-impacts between two elastic beam. J. Exp. Mech. 14(2), 129–135 (1999)

    Google Scholar 

  43. Wen, G., Huidong, X., **ao, L.: Experimental investigation of a two-degree-of-freedom vibro-impact system. Int. J. Bifurc. Chaos 22(5), 1250110 (2012)

    Article  Google Scholar 

  44. Wang, Z., Luo, T.Q.: An experimental approach based on electronic circuits for verifying dynamic mechanical behavior of a periodically-forced system with clearances. Circuits Syst. Signal Process. 36, 3835–3842 (2017)

    Article  Google Scholar 

  45. Liao, M., Ing, J., Páez Chávez, J.: Marian Wiercigroch, Bifurcation techniques for stiffness identification of an impact oscillator. Commun. Nonlinear Sci. Numer. Simul. 41, 19–31 (2016)

    Article  MathSciNet  Google Scholar 

  46. Nguyen, V.-D., Woo, K.-C., Pavlovskaia, E.: Experimental study and mathematical modelling of a new of vibro-impact moling device. Int. J. Non Linear Mech. 43(6), 542–550 (2008)

    Article  MATH  Google Scholar 

  47. Pavlovskaia, E., Hendry, D.C., Wiercigroch, M.: Modelling of high frequency vibro-impact drilling. Int. J. Mech. Sci. 91, 110–119 (2015)

    Article  Google Scholar 

  48. Ho, J.-H., Nguyen, V.-D., Woo, K.-C.: Nonlinear dynamics of a new electro-vibro-impact system. Nonlinear Dyn. 63(1–2), 35–49 (2011)

    Article  MATH  Google Scholar 

  49. Long, X.H., Liu, J.B., Meng, G.: Nonlinear dynamics of two harmonically excited elastic structures with impact interaction. J. Sound Vib. 333, 1430–1441 (2014)

    Article  Google Scholar 

  50. Piiroinen, P.T., Virgin, L.N., Champneys, A.R.: Chaos and period-adding: experimental and numerical verification of the grazing bifurcation. J. Nonlinear Sci. 14(4), 627–654 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  51. Sitnikova, E., Pavlovskaia, E., Ing, J.: Experimental bifurcations of an impact oscillator with sma constraint. Int. J. Bifurc. Chaos 22(5), 1230017 (2012)

    Article  Google Scholar 

  52. Aguiar, R.R., Weber, H.I.: Mathematical modeling and experimental investigation of an embedded vibro-impact system. Nonlinear Dyn. 65(3), 317–334 (2011)

    Article  Google Scholar 

  53. Liu, Y., Pavlovskaia, E., Wiercigroch, M.: Experimental verification of the vibro-impact capsule model. Nonlinear Dyn. 83(1), 1029–1041 (2016)

    Article  Google Scholar 

  54. Liao, M., Ing, J., Sayah, M., Wiercigroch, M.: Dynamic method of stiffness identification in impacting systems for percussive drilling applications. Mech. Syst. Signal Process. 80, 224–244 (2016)

    Article  Google Scholar 

  55. Shaw, S.W., Holmes, P.J.: A periodically forced impact oscillator with large dissipation. J. Appl. Mech. 50, 849857 (1983)

    Article  MATH  Google Scholar 

  56. Shaw, S.W., Holmes, P.J.: Periodically forced linear oscillator with impacts: chaos and long-period motions. Phys. Rev. Lett. 51(8), 623–626 (1983)

    Article  MathSciNet  Google Scholar 

  57. **e, J.H.: The mathematical model for the impact hammer and global bifurcations. Acta Mech. Sin. 29(4), 456–463 (1997)

    Google Scholar 

  58. Luo, G.W., **e, J.H.: Periodic motions and global bifurcations of a two-degree-of-freedom system with plastic impact. J. Sound Vib. 240(5), 387–858 (2001)

    Google Scholar 

  59. Luo, G.W., Lv, X.H.: Controlling bifurcation and chaos of a plastic impact oscillator. Nonlinear Anal. Real World Appl. 10(4), 2047–2061 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  60. Czolczynski, K., Blazejczyk-Okolewska, B., Okolewski, A.: Analytical and numerical investigations of stable periodic solutions of the impacting oscillator with a moving base. Int. J. Mech. Sci. 115–116, 325–338 (2016)

    Article  Google Scholar 

  61. Blazejczyk-Okolewska, B., Czolczynski, K., Kapitaniak, T.: Dynamics of a two-degree-of-freedom cantilever beam with impacts. Commun. Nonlinear Sci. Numer. Simul. 15, 1358–1367 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  62. Luo, G.W., **e, J.H.: Hopf bifurcations and chaos of a two-degree-of-freedom vibro-impact system in two strong resonance cases. Int. J. Non linear Mech. 37(1), 19–34 (2002)

    Article  MATH  Google Scholar 

  63. Wen, B.C., Liu, F.Q.: Theory and Application of Vibratory Mechanism. Mechanism Industry Press, Bei**g (1982)

    Google Scholar 

  64. Wen, B.C., Li, Y.L., Han, Q.K.: Theory and Application of Nonlinear Oscillation. Northeast University Press, Shenyang (2001)

    Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support by National Natural Science Foundation of China (11462012, 11672121) and Innovation and Entrepreneurship Talents Training Project of Lanzhou City of China (2014-RC-33).

Author information

Authors and Affiliations

  1. School of Bailie Mechanical Engineering, Lanzhou City University, Lanzhou, 730070, China

    G. W. Luo

  2. Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province, Lanzhou, 730070, China

    X. H. Lv, X. F. Zhu, Y. Q. Shi & S. S. Du

Authors
  1. G. W. Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. H. Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. X. F. Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Y. Q. Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. S. S. Du
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. W. Luo.

Appendix

Appendix

Fig. 26
figure 26

Occurrence regions of various impact motions under the condition of initial parameters (the partial enlargement and details of Fig. 2): a the parameter plane numerically obtained by scanning incrementally the forcing frequency \(\omega \); b the parameter plane numerically obtained by scanning decreasingly \(\omega \)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, G.W., Lv, X.H., Zhu, X.F. et al. Diversity and transition characteristics of sticking and non-sticking periodic impact motions of periodically forced impact systems with large dissipation. Nonlinear Dyn 94, 1047–1079 (2018). https://doi.org/10.1007/s11071-018-4409-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4409-5

Keywords

Search

Navigation