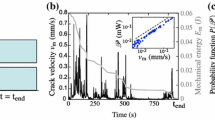
Abstract
This chapter explores the basic mechanisms underlying crack propagation in brittle heterogeneous materials and introduces tools that allow for the prediction of their effective failure properties from their microscale features. The second part of this chapter explores two fascinating features of the failure behavior of disordered materials, namely the intermittent dynamics of cracks and the roughening processes leading to the fractal structure of fracture surfaces.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
With some abuse of terminology, we will refer in the following to \(G_\textrm{c}\) as the material toughness that, strictly speaking, corresponds to the fracture energy.
- 2.
The case of cracks that can meander out of the mean fracture plane is discussed in perspectives in Sect. 2.7.
- 3.
The non-local part of the elastic energy release rate can be conveniently written in the Fourier space as \(\delta \tilde{G}(q) = - |q| G(c_0, \delta ) \delta \tilde{c}(q) \).
- 4.
The convergence of this integral is ensured under the condition \(dG_0/dc_0 < 0 \Leftrightarrow \mathcal {L} > 0\). In fact, the limiting case \(dG_0/dc_0 \rightarrow 0 \Leftrightarrow \mathcal {L} \rightarrow +\infty \), admits also a solution as long as these front perturbations are calculated from the reference configuration \(\delta c(0)\). In physical terms, it means that the structural length \(\mathcal {L}\) is much larger than the obstacle width d.
- 5.
The logarithmic evolution of the perturbation obtained for a crack pinned by a single heterogeneity can be inferred more directly by considering the application of a point force on the front that reflects the toughness distribution \(g_\textrm{c} \sim \delta (z)\) where \(\delta \) is the Dirac function. The application of the equilibrium condition Eq. (13) in the limit \(\mathcal {L} \rightarrow 0 \) gives \( \delta \tilde{c} \sim 1/|q|\) that results in the logarithmic behavior \(\delta c(z) \sim \log (|z|)\).
- 6.
The second order term calculated by this procedure takes a more compact form in Fourier space
$$\begin{aligned} \delta \tilde{G}^{(2)} [\delta \tilde{c}](q) = \int \limits _{- \infty }^{+\infty } \mathcal {Q} (q',q-q') \delta \tilde{c}(q') \delta \tilde{c}(q-q')dq' \quad {(18)} \end{aligned}$$where the kernel \(\mathcal {Q}\) follows the form
$$\begin{aligned} \begin{aligned} \mathcal {Q}&(q',\tilde{q}) = \frac{1}{2} \frac{d^2 G_0}{dc^2_0}-\frac{1}{4}\frac{dG_0}{dc_0}[|q'+\tilde{q}|+|q'|+|\tilde{q}|]+ \\&\frac{G_0}{8} \left[ \textrm{sign}(q'\tilde{q})(q'+\tilde{q})^2 + [\textrm{sign}(q')-\textrm{sign}(\tilde{q})] \, |q'+\tilde{q}| (k'- \tilde{q})-(|q'|-|\tilde{q}|)^2 \right] . \end{aligned}\quad {(19)} \end{aligned}$$.
- 7.
- 8.
Note the interesting asymptotic case \(k \rightarrow \infty \) showing a linear behavior (green line in Fig. 8). This case actually corresponds to the behavior of a semi-infinite crack pinned by a sinusoidal distribution of tough obstacles \(g_\textrm{c} = 2 C \cos (k z)\) that can be solved using Eq. (13) for \(C \ll 1\). One obtains sinusoidal front deformations \(\delta a(z) = 2C/k \cos (k z)\) of amplitude \(\Delta a/\lambda = 2C/\pi \), in agreement with the amplitude of the front perturbations of a penny-shape crack in the limit \(\lambda /a \rightarrow 0\) of very small obstacles with respect to the crack radius. As the last result is valid for any contrast, this suggests that it may also apply to the semi-infinite crack for any value of C. Ultimately, this suggests that the stiffening behavior observed in Fig. 6 and the softening behavior observed in Fig. 13 for large contrast vanish when the front deformations are negligible with respect to the structural length \(\mathcal {L}\).
- 9.
Roughly speaking, the determination of the stationnary front configuration solving the equation \(g(a(\theta )) = C g_\textrm{c}(\theta )\) consists in determining the front deformation amplitude \(\Delta a/\lambda (C)\) corresponding to the imposed contrast C (see Fig. 13). However, as the contrast increases, we expect the curves in Fig. 13 to display a vertical asymptote for the critical contrast \(C_c(k)\) shown in Fig. 12. This implies that the problem has no solution for \(C > C_c(k)\), explaining the continously growing petals observed in the fingering regime.
- 10.
The slight decrease of the effective toughness with the contrast in this regime can actually be explained quantitatively using the first order theory of Gao and Rice (1987). It allows to capture that a larger section of the front visits the weaker region of the fracture plane where the crack deforms further, leading to \(\frac{G_\textrm{c}^{\text {eff}}}{\langle G_\textrm{c} \rangle } = 1 - \frac{4}{k-1}C^2 \).
- 11.
b denotes the sample width along the z-axis.
- 12.
Strictly speaking, the effective fracture energy \(G_\textrm{c}^{\text {eff}}\) corresponds to the maximum of the instantaneous fracture energy \(G_\textrm{c}(t)\) while our calculation predicts here that the proportionality constant corresponds to its time-average \(\langle G_\textrm{c}(t) \rangle _t\).
- 13.
The length scale \(l_0 \approx 8~\upmu \text {m}\) involved in the variations of the correlation time \(\delta t^*\) with \(v_m\) is found to be of the order of one tenth of the characteristic size of the heterogeneities.
- 14.
Higher order momentum of the distribution of toughness do not play any role in the collective regime considered subsequently, as illustrated by the study of the effective toughness of disordered solids presented in Sect. 2.5.
- 15.
See Wiese and Le Doussal (2007) for a review of the appropriate analytical methods based on the Functional Renormalization Group theory. Note however that they provide only approximated solutions, strictly valid at the critical dimension \(d_c\), where d is the interface dimension with \(d_c = 2\) while \(d=1\) for crack propagation problems.
- 16.
A fit of the experimental data of Lengliné et al. (2011) with the law \(G_\textrm{c} \sim (1+ v_m/v_c)^{\gamma }\) allows for an estimation of the characteristic velocity \(v_0 \simeq 140~\upmu ~\text {m.s}^{-1}\) over the experimentally investigated range of crack speeds \(0.4~\upmu ~\text {m.s}^{-1} \le v_m \le 40~\upmu ~\text {m.s}^{-1} \), using the fitting parameters \(v_c = 5~\upmu ~\text {m.s}^{-1}\) and \(\gamma \simeq 0.07\).
- 17.
Two important assumptions have been made here. First, the depth of the largest cluster has been approximated by the depth of the total avalanche. According to our numerical observations and the one made in Lawn and Marshall (1998), this looks like a fair assumption that relies on the anisotropic spatial structure of the avalanches that extend along the front direction rather than along the propagation direction. Second, we have assumed that the velocity during the propagation of the crack over \(one cluster \) is set by the velocity \(v_0\), as observed during the depinning from a single obstacle (see Sect. 2.3).
- 18.
Note that we need to assume here that the largest avalanche size \(S^{*}_{av}\) is proportional to the largest cluster size \(S^{*}_d\). This was indeed observed by Laurson et al. (2010) who found \(S_d \sim S_{av} \) for the largest events.
- 19.
The existence of two distinct scaling regimes with exponent \(\eta _d \simeq 2.0\) for brittle failure and \(\eta _d \simeq 2.5\) for quasi-brittle crack growth also invites to discuss Barés et al. (2013)s experimental results presented in Fig. 16c. Here, a scaling law with \(\eta _d \simeq 2.5\) was reported in the depinning regime. Since such scaling actually does survive to upscaling Tallakstad et al. (2011), it is tempting to interpret this observation in terms of microscopic failure mechanism, and conjecture that microcracking does take place at a scale comparable to the grain size \(\xi \simeq 500~\upmu \text {m}\) of the sintered materials used in these experiments.
- 20.
The constant \(\Omega _c\) involved in Eq. (2.8) is chosen such that the average of \(\omega (\vec {x})\) over all \(\vec {x}\) is zero.
- 21.
The actual decomposition of the height variation computed as a scale \(\delta r\) into the sum of height variations computed at a finer scale \(\epsilon = \delta r /n\) where n is an integer writes as \( \delta h (\vec {x},\delta \vec {x}) = h(\vec {x}+\delta \vec {x}) - h(\vec {x}) = \sum _{k=1}^{n} h (\vec {x}+ \frac{k}{n} \delta \vec {x} ) - h(\vec {x} + \frac{k-1}{n} \delta \vec {x}) = \sum _{k=1}^{n} \delta h ( \vec {x} + \frac{k-1}{n} \delta \vec {x}, \frac{\delta \vec {x}}{n})\).
- 22.
Note however that the original idea of Mandelbrot et al. (1984) was to establish a correlation of the material toughness with the \(roughness exponent \), and not with a crossover length scale between two self-affine regimes as discussed here.
References
Alava MJ, Nukala PK, Zapperi S (2006) Statistical models of fracture. Adv Phys 55:349–476
Albertini G, Lebihain M, Hild F, Ponson L, Kammer DS (2021) Effective toughness of heterogeneous materials with rate-dependent fracture energy. Phys Rev Lett 127:035501
Barabási AL, Stanley HE (1995) Fractal concepts in surface growth. Cambridge University Press
Barenblatt GI (1962) The mathematical theory of equilibrium cracks in brittle fracture. Adv Appl Mech 7:55–129
Barés J, Barbier L, Bonamy D (2013) Crackling versus continuumlike dynamics in brittle failure. Phys Rev Lett 111:054301
Ben-Dayan I, Bouchbinder E, Procaccia I (2006) Random and correlated roughening in slow fracture by damage nucleation. Phys Rev E 74:046102
Boffa JM, Allain C, Hulin JP (1998) Experimental analysis of fracture rugosity in granular and compact rocks. Eur Phys J Appl Phys 2:281–289
Bonamy D (2009) Intermittency and roughening in the failure of brittle heterogeneous materials. J Phys D: Appl Phys 42:214014
Bonamy D, Bouchaud E (2011) Failure of heterogeneous materials: a dynamic phase transition? Phys Rep 498:1–44
Bonamy D, Ponson L, Prades S, Bouchaud E, Guillot C (2006) Scaling exponents for fracture surfaces in homogeneous glass and glassy ceramics. Phys Rev Lett 97:135504
Bonamy D, Santucci S, Ponson L (2008) Crackling dynamics in material failure as the signature of a self-organized dynamic phase transition. Phys Rev Lett 101:045501
Bouchaud E, Ponson L (2022) Fracture mechanics of heterogeneous materials. Wiley, Hoboken, in preparation
Bouchaud E, Lapasset G, Plan‘es J (1990) Fractal dimension of fractured surfaces: a universal value? Europhys Lett 13:73–79
Bouchaud JP, Bouchaud E, Lapasset G, Plan‘es J (1993) Models of fractal cracks. Phys Rev Lett 71:2240–2243
Bueckner HF (1970) A novel principle for the computation of stress intensity factors. ZAMM 50:529–546
Carneiro FLLB (1943) A new method to determine the tensile strength of concrete. In: Proceedings of the 5\({\rm th}\) meeting of the Brazilian association for technical rules, pp 126–129
Chopin J, Bhaskar A, Jog A, Ponson L (2018) Depinning dynamics of crack fronts. Phys Rev E 121:235501
Ciccotti M, Creton C (2016) Fracture and adhesion of soft materials: a review. Rep Prog Phys 79:0466601
Cotterell B, Rice JR (1980) Slightly curved or kinked cracks. Int J Fract 16:155–169
Dalmas D, Lelarge A, Vandembroucq D (2008) Crack propagation through phase-separated glasses: effect of the characteristic size of disorder. Phys Rev Lett 101:255501
Démery V, Rosso A, Ponson L (2014) From microstructural features to effective toughness in disordered brittle solids. EPL 105:34003
Duemmer O, Krauth W (2007) Depinning exponents of the driven longrange elastic string. J Stat Mech 1:01019
Engøy T, Måløy KJ, Hansen A, Roux S (1994) Roughness of twodimensional cracks in wood. Phys Rev Lett 73:834–837
Ertas D, Kardar M (1994) Critical dynamics of contact line depinning. Phys Rev E 49:R2532
Gao H, Rice JR (1987) Somewhat circular tensile cracks. Int J Fract 33:155–174
Gao H, Rice JR (1989) A first-order perturbation analysis of crack trap** by arrays of obstacles. J Appl Mech 56:828–836
Ghatak A, Chaudhury MK, Shenoy V, Sharma A (2000) Meniscus instability in a thin elastic film. Phys Rev Lett 85:4329–4332
Gjerden KG, Stormo A, Hansen A (2014) Local dynamics of a randomly pinned crack front: a numerical study. Front Phys 2:66
Gol’dstein RV, Salganik RL (1974) Brittle fracture of solids with arbitrary cracks. Int J Fract 10:507–523
Guerra C, Scheibert J, Bonamy D, Dalmas D (2012) Understanding fast macroscale fracture from microcrack post mortem patterns. Proc Natl Acad Sci 109:390–394
Hansen A, Schmittbuhl J (2003) Origin of the universal roughness exponent of brittle fracture surfaces: stress weighted percolation in the damage zone. Phys Rev Lett 90:045504
Hossain MZ, Hsueh CJ, Bourdin B, Bhattacharya K (2014) Effective toughness of heterogeneous media. J Mech Phys Solids 71:15–32
Irwin GR (1958) Fracture. In: Handbuch der Physik, vol 6. Springer, Berlin, p 551
Kardar M (1998) Nonequilibrium dynamics of interfaces and lines. Phys Rep 301:85–112
Katzav E, Adda-Bedia M (2006) Roughness of tensile crack fronts in heterogeneous materials. EPL 76:450–456
Katzav E, Adda-Bedia M, Derrida B (2007) Fracture surfaces of heterogeneous materials: a 2D solvable model. EPL 78:46006
Kertesz J, Horvath V, Weber F (1993) Self-affine rupture lines in paper sheet. Fractals 1:67–74
Kolvin I, Cohen G, Fineberg J (2015) Crack front dynamics: the interplay of singular geometry and crack instability. Phys Rev Lett 114:175501
Larralde H, Ball RC (1995) The shape of slowly growing cracks. Europhys Lett 30:87–92
Larkin A, Ovchinnikov Y (1979) Pinning in type II superconductors. J Low Temp Phys 34:409–428
Laurson L, Santucci S, Zapperi S (2010) Avalanches and clusters in planar crack front propagation. Phys Rev E 81:046116
Lawn BR, Marshall DB (1998) Nonlinear stress-strain curves for solids containing closed cracks with friction. J Mech Phys Solids 46:85–113
Lebihain M (2021) Towards brittle materials with tailored fracture properties: the decisive influence of the material disorder and its microstructure. Int J Frac 230:99–114
Lebihain M, Leblond JB, Ponson L (2020) Effective toughness of periodic heterogeneous materials: the effect of out-of-plane excursions of cracks. J Mech Phys Solids 137:103876
Lebihain M, Ponson L, Kondo D, Leblond JB (2021) Effective toughness of disordered brittle solids: a homogenization framework. J Mech Phys Solids 153:104463
Leblond JB, Ponson L (2016) Out-of-plane deviation of a mode I+III crack encountering a tougher obstacle. C R Mécanique 344:521–531
Lengliné O, Toussaint R, Schmittbuhl J, Elkhoury JE, Ampuero JP, Tallakstad KT, Santucci S, Måløy KJ (2011) Average crack-front velocity during subcritical fracture propagation in a heterogeneous medium. Phys Rev E 84:036104
Leschhorn H, Nattermann T, Stepanow S, Tang LH (1997) Driven interface depinning in a disordered medium. Ann Phys 6:1–34
Lockner DA, Byerlee JB, Kiksenko V, Ponomarev A, Sidorin A (1991) Quasi-static fault growth and shear fracture energy in granite. Nature 350:39–42
Måløy KJ, Schmittbuhl J (2001) Dynamical event during slow crack propagation. Phys Rev Lett 87:105502
Måløy KJ, Hansen A, Hinrichsen EL, Roux S (1992) Experimental measurements of the roughness of brittle cracks. Phys Rev Lett 68:213–215
Måløy KJ, Santucci S, Schmittbuhl J, Toussaint R (2006) Local waiting time fluctuations along a randomly pinned crack front. Phys Rev Lett 96:045501
Mandelbrot BB, Passoja DE, Paullay AJ (1984) Fractal character of fracture surfaces of metals. Nature 308:721–722
Morel S, Lubet T, Pouchou JL, Olive JM (2004) Roughness analysis of the cracked surfaces of a face centered cubic alloy. Phys Rev Lett 93:065504
Morel S, Bonamy D, Ponson L, Bouchaud E (2008) Transient damage spreading and anomalous scaling in mortar crack surfaces. Phys Rev E 78:016112
Movchan AB, Gao H, Willis JR (1998) On perturbations of plane cracks. Int J Solids Struct 35:3419–3453
Nattermann T, Stepanow S, Tang LH, Leschhorn H (1992) Dynamics of interface depinning in a disordered medium. J Phys II Franc 2:1483–1488
Nukala PKVV, Barai P, Zapperi S, Alava M, Simunovic S (2010) Fracture roughness in three-dimensional beam lattice systems. Phys Rev E 82:026103
Osovski S, Sristava A, Ponson L, Bouchaud E, Tvergaard V, Ravi-Chandar K, Needleman A (2015) The effect of loading rate on ductile fracture toughness and fracture surface roughness. J Mech Phys Solids 76:20–46
Overvelde JTB, Bertoldi K (2014) Relating pore shape to the nonlinear response of periodic elastomeric structures. J Mech Phys Solids 64:351–366
Patinet S, Vandembroucq D, Roux S (2013) Quantitative prediction of effective toughness at random heterogeneous interfaces. Phys Rev Lett 110:165507
Ponson L (2009) Depinning transition in the failure of inhomogeneous brittle materials, Phys Rev Lett 103:055501
Ponson L (2016) Statistical aspects in crack growth phenomena: how the fluctuations reveal the failure mechanisms. Int J Fract 201:11–27
Ponson L, Bonamy D (2010) Crack propagation in brittle heterogeneous solids: material disorder and crack dynamics. Int J Fract 162:21–31
Ponson L, Pindra N (2017) Crack propagation through disordered materials as a depinning transition: a critical test of the theory. Phys Rev E 95:053004
Ponson L, Bonamy D, Bouchaud E (2006) Two-dimensional scaling properties of experimental fracture surfaces. Phys Rev Lett 96:035506
Ponson L, Bonamy D, Auradou H, Mourot G, Morel S, Bouchaud E, Guillot C, Hulin JP (2006) Anisotropic self-affine properties of experimental fracture surfaces. Int J Fract 140:27–36
Ponson L, Auradou H, Vié P, Hulin JP (2006) Low self-affine exponents of fractured glass ceramics surfaces. Phys Rev Lett 97:125501
Ponson L, Auradou H, Pessel M, Lazarus V, Hulin J-P (2007) Failure mechanisms and surface roughness statistics of fractured fontainebleau sandstone. Phys Rev E 76:036108
Ponson L, Cao Y, Bouchaud E, Tvergaard V, Needleman A (2013) Statistics of ductile fracture surfaces: the effect of material parameters. Int J Fract 184:137–149
Ponson L, Shabir Z, Van der Giessen E, Simone A (2021) Unified scenario for the morphology of crack paths in two-dimensional disordered solids. Phys Rev E 104:055003
Poon B, Ponson L, Zhao J, Ravichandran G (2011) Damage accumulation and hysteretic behavior of max phase materials. J Mech Phys Solids 59:2238–2257
Pouchou JL, Boivin D, Beauchêne P, Le Besnerais G, Vignon F (2002) 3D reconstruction of rough surfaces by SEM stereo imaging. Microchimica Acta 139:135–144
Ramanathan S, Ertas D, Fisher DS (1997) Quasistatic crack propagation in heterogeneous media. Phys Rev Lett 79:873–876
Rice JR (1989) Weight function theory for three-dimensional elastic crack analysis. In: Wei, Gangloff (eds) Fracture mechanics: perspectives and directions, ASTM STP 1020. American Society for Testing and Materials, pp 29–57
Rice JR (1985) First-order variation in elastic fields due to variation in location of a planar crack front. J Appl Mech 52:571–579
Rosso A, Krauth W (2001) Monte carlo dynamics of driven elastic strings in disordered media. Phys Rev B 65:012202
Rosso A, Krauth W (2001) Origin of the roughness exponent in elastic strings at the depinning threshold. Phys Rev Lett 87:187002
Roux S, Vandembroucq D, Hild F (2003) Effective toughness of heterogeneous brittle materials. Eur. J. Mech. A Solids 22:743–749
Roux S, Hild F (2008) Self-consistent scheme for toughness homogenization. Int J Fract 154:159–166
Saffman PG, Taylor GI (1958) The penetration of a fluid into a porous medium of hele-shaw cell containing a more viscous liquid. Proc R Soc Lond A 245:312
Saintyves B, Dauchot O, Bouchaud E (2013) Bulk elastic fingering instability in hele-shaw cells. Phys Rev Lett 111:047801
Salminen LI, Alava M, Niskanen KJ (2003) Analysis of long crack lines in paper webs. Eur Phys J B 32:369–374
Santucci S, Måløy KJ, Delaplace A, Mathiesen J, Hansen A, Bakke J, Schmittbuhl J, Vanel L, Ray P (2007) Statistics of fracture surfaces. Phys Rev E 75:016104
Srivastava A, Ponson L, Osovski S, Bouchaud E, V Tvergaard, Needleman A (2014) Effect of inclusion density on ductile fracture toughness and roughness. J Mech Phys Solids 63:62–79
Stojanova M, Santucci S, Vanel L, Ramos O (2014) High frequency monitoring reveals aftershocks in subcritical crack growth. Phys Rev Lett 112:115502
Tallakstad KT, Toussaint R, Santucci S, Schmittbuhl J, Måløy KJ (2011) Local dynamics of a randomly pinned crack front during creep and forced propagation: an experimental study. Phys Rev E 83:046108
Tallakstad KT, Toussaint R, Santucci S, Måløy KJ (2013) Non-gaussian nature of fracture and the survival of fat-tail exponents. Phys Rev Lett 110:145501
Vasoya M, Leblond JB, Ponson L (2013) A geometrically nonlinear analysis of coplanar crack propagation in some heterogeneous medium. Int J Solids Struct 50:371–378
Vasoya M, Unni AB, Leblond JB, Lazarus V, Ponson L (2016) Finite size and non-linear effects during crack pinning by heterogeneities: an analytical and experimental study. J Mech Phys Sol 89:211
Vasoya M, Lazarus V, Ponson L (2016) Bridging micro to macroscale fracture properties in highly heterogeneous brittle solids: weak pinning versus fingering. J Mech Phys Solids 95:755–773
Vernède S, Ponson L, Bouchaud J-P (2015) Turbulent fracture surfaces: a footprint of damage percolation? Phys Rev Lett 141:215501
Vernède S, Ponson L (2017) Method for characterizing the cracking mechanism of a material from the fracture surfaces thereof. French patent 1459525 (2014), European, US and Chinese patent
Ververis C, Georghiou K, Christodoulakis N, Santas P, Santas R (2004) Fiber dimensions, lignin and cellulose content of various plant materials and their suitability for paper production. Ind Crop Prod 19:245–254
Vincent-Dospital T, Cochard A, Santucci S, Maloy KJ, Toussaint R (2021) Thermallu activated intermittent dynamics of cree** crack fronts along disordered interfaces. Sci Rep 11:20418
Wang N, **a S (2017) Cohesive fracture of elastically heterogeneous materials: an integrative modeling and experimental study. J Mech Phys Solids 98:87–105
Wiese K, Le Doussal P (2007) Functional renormalization for disordered systems. Basic recipes and gourmet dishes. In: Markov processes and related fields, vol 13. Polymath, pp 777–818
**a S, Ponson L, Ravichandran G, Bhattacharya K (2012) Toughening and asymmetry in peeling of heterogeneous adhesives. Phys Rev Lett 108:196101
**a S, Ponson L, Ravichandran G, Bhattacharya K (2013) Adhesion of heterogeneous thin. I: elastic heterogeneity. J Mech Phys Solids 61:838–851
**a S, Ponson L, Ravichandran G, Bhattacharya K (2015) Adhesion of heterogeneous thin. II: adhesive heterogeneity. J Mech Phys Solids 83:88–103
Zapperi S (2012) Current challenges for statistical physics in fracture and plasticity. Eur Phys J B 85:829
Acknowledgements
The author would like to dedicate this chapter to my younger collaborators, Aditya Vasudevan, Ashwij Mayya, Estelle Berthier, Guillaume de Luca, Julien Chopin, Manish Vasoya, Thiago Grabois and Vincent Démery without who this research would not have been possible. A special thank to Guillaume de Luca who provided a precious help in the editing of this book.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 CISM International Centre for Mechanical Sciences
About this chapter
Cite this chapter
Ponson, L. (2023). Fracture Mechanics of Heterogeneous Materials: Effective Toughness and Fluctuations. In: Ponson, L. (eds) Mechanics and Physics of Fracture. CISM International Centre for Mechanical Sciences, vol 608. Springer, Cham. https://doi.org/10.1007/978-3-031-18340-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-18340-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-18339-3
Online ISBN: 978-3-031-18340-9
eBook Packages: EngineeringEngineering (R0)