Electrically tunable total reflection of light by oblique helicoidal cholesteric

Abstract

An oblique helicoidal state of a cholesteric liquid crystal (Ch_OH) is capable of continuous change of the pitch $P$ in response to an applied electric field. Such a structure reflects 50% of the unpolarized light incident along the Ch_OH axis in the electrically tunable band determined by $P$/2. Here, we demonstrate that at an oblique incidence of light, Ch_OH reflects 100% of light of any polarization. This singlet band of total reflection is associated with the full pitch $P$. We also describe the satellite $P/2$, $P/3$, and $P/4$ bands. The $P/2$ and $P/4$ bands are triplets, whereas $P/3$ band is a singlet caused by multiple scatterings at $P$ and $P/2$. A single Ch_OH cell acted upon by an electric field tunes all these bands in a very broad spectral range, from ultraviolet to infrared and beyond, thus representing a structural color device with enormous potential for optical and photonic applications.

Impact statement

Pigments, inks, and dyes produce colors by partially consuming the energy of light. In contrast, structural colors caused by interference and diffraction of light scattered at submicrometer length scales do not involve energy losses, which explains their widespread in Nature and the interest of researchers to develop mimicking materials. The grand challenge is to produce materials in which the structural colors could be dynamically tuned. Among the oldest known materials producing structural colors are cholesteric liquid crystals. Light causes coloration by selective Bragg reflection at the periodic helicoidal structure formed by cholesteric molecules. The cholesteric pitch and thus the color can be altered by chemical composition or by temperature, but, unfortunately, dynamic tuning by electromagnetic field has been elusive. Here, we demonstrate that a cholesteric material in a new oblique helicoidal Ch_OH state could produce total reflection of an obliquely incident light of any polarization. The material reflects 100% of light within a band that is continuously tunable by the electric field through the entire visible spectrum while preserving its maximum efficiency. Broad electric tunability of total reflection makes the Ch_OH material suitable for applications in energy-saving smart windows, transparent displays, communications, lasers, multispectral imaging, and virtual and augmented reality.

Graphical Abstract

Introduction

The development of materials capable of dynamically controlled transmission and reflection of light or, more generally, electromagnetic radiation, is one of the most important directions of research with potential applications, such as energy-saving smart windows, transparent displays, communications, lasers, multispectral imaging, and virtual and augmented reality.^1,2,3,4 A challenging problem is to formulate materials in which light is controlled through the “structural colors” concept, using interference, diffraction, and scattering at submicron-scale architectures, as opposed to absorption. Cholesteric (Ch) liquid crystals (LCs) are among the best-known structurally colored media.^5,6,7,8,9 They are formed by chiral elongated organic molecules that arrange into a helical structure, in which the local molecular orientation $\widehat{{\textbf{{n}}}}$ twists around a helicoidal axis $\widehat{{\textbf{h}}}$ remaining perpendicular to it. Spatial modulation of the refractive indices with the period ${P}_{0}$/2, where the pitch ${P}_{0}$ is the distance over which the director $\widehat{{\textbf{{n}}}}$ rotates by 360° (Figure 1a), enables selective reflection of light,^10,11,12 a property attractive for applications.^5,6,7,13 For normal incidence, 50% of unpolarized light is reflected at the half-pitch ${P}_{0}/2$; the other 50% are transmitted. The reflected light is circularly polarized with the same handedness as the Ch, whereas the transmitted light is of opposite circular polarization. Resulting structural Ch colors are highly saturated, they add as colored lights and produce a color gamut greater than that obtained with inks, dyes, and pigments.¹⁴ For oblique incidence of light, more than 50% of light can be reflected, as first reported by Fergason¹⁵ and reviewed recently by Tondiglia et al.¹⁶

Figure 1

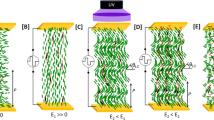
Schematic drawing of (a) a ground Ch state in the absence of the electric field and (b–e) field-induced states in the Ch_OH material: (b) a light-scattering “fingerprint” Ch state stabilized by a weak electric field E < E_N*C, (c, d) Ch_OH structure with a heliconical angle θ and a pitch P both E-tunable in the range E_N*C ≤ E < E_NC (both θ and P decrease when the field E increases), and (e) an unwound state with θ  = 0 and the director $\widehat{{\textbf{n}}}$ aligned parallel to a strong applied field E ≥ E_NC. (f) Top view of the experimental setup. The Ch_OH cell is mounted in the center of the goniometer stage with cell’s xy surface being perpendicular to the plane xz of light incidence. The vectors E_p and E_s correspond to p- and s-polarizations of the incident light, respectively. The polarizers P control polarization of the incident beams, while the analyzer A is used to explore the polarization of reflected/transmitted beams. The angle of light incidence $\upbeta$ is measured from the normal $\widehat{\mathbf{z}}$ to the Ch_OH cell. (g) Schematic drawing of the Ch_OH cell subject to an applied AC field, 3 kHz.

Unfortunately, these structural colors are hard to tune by an electric or magnetic field since the conventional right-angle Ch helix loses its single-mode optical modulation in the presence of the field.⁹ One approach is to use polymer-cholesteric composites^13,16,17 and to control the structure through the polymer component. For example, one can use a Ch with a positive dielectric anisotropy to switch between a state with selective reflection and a state with polydomain scattering structure,¹³ or use a Ch with a negative dielectric anisotropy and change the pitch through an electromechanical shift of the ionic polymer network.^18,19

A direct electromagnetic tuning of Ch structural colors is made possible by the materials with positive dielectric anisotropy that adopt a peculiar oblique helicoidal cholesteric (Ch_OH) structure^{20,21,22,23,24,25,26,27,28,29} (Figure 1c–d). The Ch_OH state forms only in the presence of the electric or magnetic field.^20,21,30,31 While a weak field orients the helicoidal axis $\widehat{{\textbf{h}}}$ perpendicular to itself forming a light-scattering “fingerprint” Ch state⁹ (Figure 1b), a field above some threshold E_N*C realigns $\widehat{{\textbf{h}}}$ parallel to itself and forms a heliconical Ch_OH structure in which $\widehat{{\textbf{n}}}$ twists around $\widehat{{\textbf{h}}}$, being also tilted to it^20,21,30,31 (Figure 1c–d). The tilt implies that $\widehat{{\textbf{n}}}$ twists and bends.³² Because of this, the Ch_OH is stable only when the bend elastic constant ${K}_{33}$ is smaller than its twist ${K}_{22}$ counterpart, as demonstrated theoretically by Meyer and de Gennes.^30,31 A crucial advantage of the heliconical Ch_OH over the right-angle Ch is that the pitch could be continuously tuned by changing the amplitude of the applied field. Because $\widehat{{\textbf{h}}}$ is parallel to the field, Ch_OH preserves the single-mode character of the refractive-index modulation, which guarantees a high efficiency of reflection within a very broad range, from ultraviolet to infrared, including the entire visible spectrum^{20,21,22,23,33} (Figure 1c–d). At very high fields, the heliconical structure is unwound into a uniformly aligned director^20,21,22,33 (Figure 1e).

The electrically controlled optical properties of Ch_OH have been studied for normal incidence of light.^{20,21,22,23,33} At the normal incidence, reflection and transmission are defined by the Ch_OH half-pitch P/2, similar to the case of Ch. Oblique propagation of light should reveal the true period P since the propagating wave distinguishes molecular tilts away and toward itself. Oblique incidence of light has been studied theoretically^34,35,36,37 and experimentally in the structural analog of Ch_OH, the chiral smectic C (SmC*).^{38,39,40,41,42,43} SmC* is formed by molecular layers stacked on top of each other. The molecules are tilted with respect to normal to the layers, so that the director $\widehat{{\textbf{n}}}$ experiences heliconical modulation along this normal. Berreman³⁵ simulated numerically propagation of light in SmC* for the incident angle 45° and discovered reflections from $P$ and $P$/3, in addition to the reflection from $P$/2 observed also at the normal incidence. The $P$/2 band produces reflections with p- and s-polarizations for both p- and s-polarized incident beams. The reflections at $P$ and $P$/3 are different: the p-polarized incident light produces only an s-polarized reflection and vice versa. Berreman admitted that “a convincing intuitive argument for this very odd result” could not be given.^34,35 Experiments by Hori^38,39 confirmed the polarization features of reflections at $P$ and $P$/2 and demonstrated that the reflection from $P$ could reach 100% efficiency for an unpolarized beam.³⁹ Ouchi et al.³⁶ derived the dispersion relation for the optical eigenmodes in SmC* and demonstrated the observed experimental features of reflections at $P$ and $P$/2. The theory was expanded by Oldano et al.³⁷ who considered the electromagnetic waves as a superposition of eigenmodes, which are the Bloch waves corresponding to the periodic SmC* structure, and predicted that reflections at $P/N$ exhibit different polarization properties for odd and even values of the integer $N$. Namely, even $N$s produce reflection bands in the shape of triplets, whose central peak is common to both eigenmodes and corresponds to total reflection with a polarization exchange; the lateral peaks correspond to the Bragg reflection of each eigenmode. The odd $N$s result in singlets whose characteristics are very similar to the central peak of the triplets.³⁷ Further experiments by Ozaki et al. demonstrated the $P$-band reflection tunability by changing the incident angle, the temperature, or the electric field applied perpendicularly to the helicoidal axis $\widehat{{\textbf{h}}}$ of SmC*.^40,41,42,43 The electrically tunable range achieved in Reference 43 was ~70 nm.

Despite the structural similarities of SmC* and Ch_OH, their pitch tunability is different. The SmC* exhibits a helicoidal wave of electric polarization; its periodicity could be changed by applying an electric field perpendicularly to $\widehat{{\textbf{h}}}$. However, the field applied in this direction expands regions with favorable direction of polarization and shrinks the regions of unfavorable polarization, thus destroying the single-mode modulation of the director and diminishing the efficiency of Bragg reflection. This limitation is lifted in the Ch_OH: since the field acts along the helicoidal axis $\widehat{{\textbf{h}}}$, it changes the pitch and the conical tilt angle without distorting the single-mode modulation of the optic tensor, which yields highly efficient tunability by hundreds of nanometers.^20,21,22

In this work, we explore theoretically and experimentally Bragg reflection of light incident obliquely on the Ch_OH (Figure 1). Previous studies of SmC* are based on numerical modeling. In the present work, taking advantage of a relatively weak birefringence, we develop a coupled wave model with effective resonance matrices, which predicts analytically the locations, intensities, widths, and polarization properties of the reflection bands in the entire range of incident and conical angles. This analytical approach allows one to analyze the properties of reflection as a function of relevant material parameters. This advantage over the purely numerical approach is especially useful for Ch_OH, in which the material parameters such as the conical angle and pitch can be varied in a broad range by the electric field. The predicted multiple reflection bands corresponding to the pitch $P$, half-pitch $P/2$, one-third of the pitch $P/3,$, and a quarter of the pitch $P/4$ are observed and characterized experimentally (Figures 2–6). Bragg reflection at $P$ maintains 100% efficiency for any polarization of light, while its band position is tuned by the electric field in a broad spectral range, embracing hundreds of nanometers (Figure 4a). Because the optic tensor contains only two spatial harmonics corresponding to $P$ and $P/2$, reflections at $P/3$ and $P/4$ are caused by multiple scatterings at $P$ and $P/2$. The observed structure and polarization properties of the Bragg bands are explained qualitatively and quantitatively by the developed model and allow one to determine the pitch and the conical angle of the oblique helicoid. In particular, the difference between the reflection bands with a singlet peak ($N =\mathrm{1,3})$ (Figure 2b, d, e) and the triplet peaks ($N =\mathrm{2,4})$ (Figure 2c, f, g and Figure 6a, d) is explained by zero diagonal values of the effective resonance matrices for odd $N$s. Broad electric tunability and an efficient 100% reflection make the Ch_OH material highly promising for dynamic optical and photonic devices.

Theory of light propagation in Ch_OH structure

We consider EM wave propagation in a sandwich-type Ch_OH cell where the dielectric tensor at optical frequencies (optic tensor) ${\varvec{\upvarepsilon}}$ depends only on the $z$ coordinate normal to the substrates, and $xz$ is the incidence plane (Figure 1f–g). For a monochromatic wave $\propto e^{ - i\omega t}$, the homogeneity in the $xy$ plane preserves the in-plane wave vector ${\textbf{q}} =\upnu {n}_{g}{\text{sin}}{\upbeta }_{g}\widehat{{\textbf{x}}}$, where $\upnu =\upomega /c =2\uppi /\uplambda$ is the free space wave number, ${n}_{g}$ is the refractive index of the glass substrate, ${\upbeta }_{g}$ is the incidence angle in the substrate calculated from the z-axis, and $\widehat{{\mathbf{x}}}$ is the unit vector along the x-axis. Using the 4 × 4 formalism,³⁴ we obtain the solution of the Maxwell equations in the form of 4-vector z-dependent amplitudes $\left({E}_{x},{E}_{y},{H}_{y},-{H}_{x}\right){\text{exp}}(iqx )$, where ${\textbf{F}} =\left({E}_{x},{E}_{y},{H}_{y},-{H}_{x}\right)$ obeys the equation:

$$\frac{{\partial {\textbf{F}}}}{\partial z} = i{\textbf{L}} \cdot \, {\textbf{F}},$$

(1)

and the 4 × 4 matrix ${\textbf{L}}$ is

$${\textbf{L}} = \left( {\begin{array}{*{20}c} { - \frac{{q\upvarepsilon_{31} }}{{\upvarepsilon_{33} }}} & { - \frac{{q\upvarepsilon_{32} }}{{\upvarepsilon_{33} }}} &{\upnu - \frac{{q^{2} }}{{\upnu \upvarepsilon_{33} }}} & 0 \\ 0 & 0 & 0 & \upnu \\ {\upnu \left( {\frac{{\upvarepsilon_{11} - \upvarepsilon_{13} \upvarepsilon_{31} }}{{\upvarepsilon_{33} }}} \right)} & {\upnu \left( {\frac{{\upvarepsilon_{12} - \upvarepsilon_{13} \upvarepsilon_{32} }}{{\upvarepsilon_{33} }}} \right)} & { - \frac{{q\upvarepsilon_{13} }}{{\upvarepsilon_{33} }}} & 0 \\ {\upnu \left( {\frac{{\upvarepsilon_{21} - \upvarepsilon_{23} \upvarepsilon_{31} }}{{\upvarepsilon_{33} }}} \right)} & {\upnu \left( {\frac{{\upvarepsilon_{22} - \upvarepsilon_{23} \upvarepsilon_{32} }}{{\upvarepsilon_{33} }}} \right) - \frac{{q^{2} }}{\upnu }} & { - \frac{{q\upvarepsilon_{23} }}{{\upvarepsilon_{33} }}} & 0 \\ \end{array} } \right)\,\,.$$

(2)

In the uniform Ch_OH, the optic tensor ${\varvec{\upvarepsilon}}$ is determined by the constant heliconical angle θ and the uniformly rotating azimuthal angle $\upvarphi = \uptau z$,

$${\varvec{\upvarepsilon}} = n_{o}^{2} \left( {\begin{array}{*{20}c} {1 + 2\updelta \sin^{2} \uptheta \cos^{2} \upvarphi } & {\updelta \sin^{2} \uptheta \sin 2\upvarphi } & {\updelta \sin 2\uptheta \cos \upvarphi } \\ {\updelta \sin^{2} \uptheta \sin 2\upvarphi } & {1 + 2\updelta \sin^{2} \uptheta \sin^{2} \upvarphi } & {\updelta \sin 2\uptheta \sin \upvarphi } \\ {\updelta \sin 2\uptheta \cos \upvarphi } & {\updelta \sin 2\uptheta \sin \upvarphi } & {1 + 2\updelta \cos^{2} \uptheta } \\ \end{array} } \right),$$

(3)

where $\uptau =\frac{2\pi }{P}$ is the main harmonic of the periodic structure, $\updelta =\frac{\left({n}_{e}^{2}-{n}_{o}^{2}\right)}{2{n}_{o}^{2}}\approx \frac{\left({n}_{e}-{n}_{o}\right)}{{n}_{o}}$ is the relative birefringence, and ${n}_{e}$ and ${n}_{o}$ are the extraordinary and ordinary refractive indices, respectively. When $\uptheta = {\text{const}}$, $\upvarepsilon_{33} = {\text{const}}$ and Equation 1 can be reduced to a dimensionless wave equation for $\left({E}_{x},{E}_{y}\right)$ by introducing the dimensionless coordinate $\widetilde{z} =\uptau z$ and expressing ${H}_{y}$ and ${H}_{x}$ from the first and second rows of Equation 1, respectively:

$$\begin{gathered} E_{x}^{{\prime \prime }} + 2ib_{{1x}} \left( {2\cos \tilde{z}E_{x}^{\prime } + \sin \tilde{z}E_{y}^{\prime } } \right) + \left( {a_{x}^{2} - 2ib_{{1x}} \sin \tilde{z} + 2b_{{2x}} \cos 2\tilde{z}} \right)E_{x} + 2\left( {ib_{{1x}} \cos \tilde{z} + b_{{2x}} \sin 2\tilde{z}} \right)E_{y} = 0, \hfill \\ E_{y}^{{\prime \prime }} + 2ib_{{1y}} \sin \tilde{z}E_{x}^{\prime } + 2b_{{2y}} {\mkern 1mu} \sin 2\tilde{z}E_{x} + (a_{y}^{2} - 2b_{{2y}} {\mkern 1mu} \cos 2\tilde{z})E_{y} = 0, \hfill \\ \end{gathered}$$

(4)

where ${\prime} =$ $\partial /\partial \widetilde{z}$, and a factor 2 simplifies the equations for Fourier harmonics below. The coefficients in Equation 4 are defined by $\updelta$, $\uptheta$, the normalized wave number $\upeta =\frac{{n}_{o}\upnu }{\uptau } =\frac{{n}_{o}P}{\uplambda }$, and the “ordinary” angle of light incidence $\upbeta_{o} = \arcsin \left( {\frac{q}{{n_{o} \nu }}} \right) = \arcsin \left( {\frac{{n_{g} \sin \upbeta_{g} }}{{n_{o} }}} \right)$, which is very close to the angle ${\upbeta }_{g}$ of light propagation in the glass; furthermore,

$$\begin{gathered} a_{x}^{2} = \upeta ^{2} g_{x} \left( {\cos ^{2} \upbeta _{o} \left( {1 + \updelta \sin ^{2} \uptheta } \right) + 2\updelta \cos ^{2} \uptheta } \right), \hfill \\ a_{y}^{2} = \upeta ^{2} g_{y} \cos ^{2} \upbeta _{o} \left( {\cos ^{2} \upbeta _{o} + \updelta + \updelta \cos ^{2} \uptheta } \right), \hfill \\ b_{{1x}} = b_{1} g_{x} ,b_{{2x}} = b_{2} g_{x} ,b_{{1y}} = b_{1} g_{y} ,b_{{2y}} = b_{2} g_{y} , \hfill \\ \end{gathered}$$

(5)

where $g_{x}^{ - 1} = 1 + 2\updelta cos^{2} \uptheta,$ $g_{y}^{ - 1} = \cos^{2} \upbeta_{o} + 2\updelta \cos^{2} \uptheta,$ $b_{1} = \frac{\updelta \upeta }{2}\sin \upbeta_{o} \sin 2\uptheta,$ and $b_{2} = \frac{{\updelta \upeta^{2} }}{2}\cos^{2} \upbeta_{o} \sin^{2} \uptheta.$

Equation 4 is a system of linear ordinary differential equations with periodic coefficients. Therefore, its solution is a Bloch wave expressed as a series of harmonics:

$${\textbf{E}}\left( {\tilde{z}} \right) = \left( {\begin{array}{*{20}c} {E_{x} \left( {\tilde{z}} \right)} \\ {E_{y} \left( {\tilde{z}} \right)} \\ \end{array} } \right) = e^{{ik\tilde{z}}} \sum\nolimits_{m = - \infty }^{\infty } {{\textbf{E}}^{\left( m \right)} e^{{im\tilde{z}}} },$$

(6)

where the vector amplitudes ${{\textbf{E}}}^{(m)}$ obey the equation

$$\sum\nolimits_{p = - 2}^{2} {{\textbf{M}}_{p} \left( m \right){\textbf{E}}^{{\left( {m + p} \right)}} } = 0,$$

(7)

with the matrix ${{\textbf{M}}}_{p}\left(m\right)$ representing the pth harmonic of the periodic optical properties of Ch_OH,

$$\begin{gathered} {\textbf{M}}_{0} \left( m \right) = \left( {\begin{array}{*{20}c} {a_{x}^{2} - (k + m)^{2} } & 0 \\ 0 & {a_{y}^{2} - (k + m)^{2} } \\ \end{array} } \right), \hfill \\ {\textbf{M}}_{ \pm 1} \left( m \right) = \left( {\begin{array}{*{20}c} { - b_{1x} \left( {2k + 2m \mp 1} \right)} & { \mp ib_{1x} \left( {k + m} \right)} \\ { - ib_{1y} \left( {1 \pm \left( {k + m} \right)} \right)} & 0 \\ \end{array} } \right), \hfill \\ {\textbf{M}}_{ \pm 2} \left( m \right) = {\textbf{M}}_{ \pm 2} = \left( {\begin{array}{*{20}c} {b_{2x} } & { \pm ib_{2x} } \\ { \pm ib_{2y} } & { - b_{2y} } \\ \end{array} } \right). \hfill \\ \end{gathered}$$

(8)

The four nontrivial solutions of Equation 7 are invariant under the transformation ${\textbf{E}}^{( m) } \to {\textbf{E}}^{{( {m + l} )}}$ and $k \to k - l$, thus we analyze the solutions in which ${{\textbf{E}}}^{(0)}$ have the largest amplitudes.

Since ${b}_{n\upxi }\propto \updelta \approx 0.1$ (here, the subscripts adopt all possible values, $n =\mathrm{1,2}, \upxi =x,y$), ${{\textbf{M}}}_{p}\left(m\right)$ with $p\ne 0$ are small and the harmonics ${{\textbf{E}}}^{(m)}$ are mostly controlled by $u =\left({a}_{x}^{2}+{a}_{y}^{2}\right)/2 ={n}_{\text{eff}}^{2}{\upeta }^{2}$ and $v =\left({a}_{x}^{2}-{a}_{y}^{2}\right)/2 ={\updelta }_{\text{eff}}{\upeta }^{2}$, where ${n}_{\text{eff}}$ and ${\updelta }_{\text{eff}}$ are the homogeneous effective refractive index and birefringence, respectively,

$$\begin{array}{*{20}c} {n_{\text{eff}}^{2} = \cos^{2} \upbeta_{o} + \frac{\updelta }{2}\left( {\frac{{\sin^{2} \uptheta \cos^{2} \upbeta_{o} }}{{ {\cos^{2} \upbeta_{o} + 2\updelta \cos^{2} \uptheta } }} + \frac{{4\cos^{4} \uptheta - \cos^{2} \upbeta_{o} \left( {1+3\cos 2\uptheta} \right)}}{{2\left( {1 + 2\updelta \cos^{2} \uptheta } \right)}}} \right),} \\ {\updelta_{\text{eff}} = \frac{{\updelta \sin^{2} \upbeta_{o} \left[ {\cos^{2} \upbeta_{o} \left( {1+3\cos 2\uptheta} \right) + 8\updelta \cos^{4} \uptheta } \right]}}{{4\left( {1 + 2\updelta \cos^{2} \uptheta } \right)\left( {\cos^{2} \upbeta_{o} + 2\updelta \cos^{2} \uptheta } \right)}} \approx \frac{1}{4}\updelta \upeta^{2} \sin^{2} \upbeta_{o} \left( {1+3\cos 2\uptheta} \right).} \\ \end{array}$$

(9)

Note that ${\updelta }_{\text{eff}}$ and $v$ (1) change the sign at $\uptheta \approx 53^\circ$,⁴⁴ being positive in the Ch_OH with $\uptheta < 33^\circ$ and negative in the right-angle Ch with $\uptheta = 90^\circ$ and (2) decrease when $\upbeta_{o}$ decreases and completely vanish for the normal incidence.

Far from the Nth order Bragg conditions $k =N/2$, one can reduce Equation 7 to

$$\overline{\bf{M}}_{0} {\textbf{E}}^{\left( 0 \right)} = 0$$

(10)

for the dominant harmonic ${{\textbf{E}}}^{(0)}$, where $\overline{\textbf{M}}_{0} = - k^{2} {\textbf{I}} + \user2{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\textbf{M}} },$ $\mathbf{I} ={\text{diag}}(\mathrm{1,1})$ is the 2D identity matrix, and $\user2{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\textbf{M}} }$ is the perturbation expansion in $\updelta$ that results in the polynomial:

$$\user2{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\textbf{M}} } = \text{diag}\left( {a_{x}^{2} ,a_{y}^{2} } \right) - \mathop {\sum\nolimits_{l \ne 0} {{\textbf{M}}_{l} \left( 0 \right){\textbf{M}}_{0}^{ - 1} \left( l \right){\textbf{M}}_{ - l} \left( l \right) + O\left( {\updelta^{3} } \right)} }\limits_{{}}.$$

(11)

The eigenmodes’ wave vectors ${k}_{{\text{j}}}$ are the eigenvalues for $\user2{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{\textbf{M}}} }$

$$k_{ \mp , \pm } = \mp \sqrt {\frac{1}{2}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,1} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,2} \pm \sqrt {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,1} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,2} } \right)^{2} + 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,1} } } \right)}$$

(12)

and determine their polarizations through Equation 10; here and below, the subscripts $\mp$ and $\pm$ on the left-hand side of Equation 12 correspond to $\mp$ and $\pm$ on the right-hand side, respectively.

If ${\upbeta }_{o}>{\upbeta }_{c}$, where ${{\text{sin}}}^{2}{\upbeta }_{c}\approx \left|\frac{\updelta {\upeta }^{3}{{\text{sin}}}^{4}\uptheta }{\left(1-{\upeta }^{2}\right)\left(1+3{\text{cos}}2\uptheta \right)}\right|$ is determined from the condition $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,1} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,2} } \right)^{2} = 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,1},$ then the propagating forward eigenmodes are linearly polarized, being the ordinary s mode ${E}_{x,z}^{\left(0\right)} =0$ with $k_{s} = k_{ + , - } \approx \sqrt {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{2,2} } \approx a_{y}$ and the extraordinary p mode ${E}_{y}^{\left(0\right)} =0$ with $k_{p} = k_{ + , + } \approx \sqrt {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{M}_{1,1} } \approx a_{x}.$ When ${\upbeta }_{o}<{\upbeta }_{c}$ and decreases, the ellipticity increases, reaching the circular polarization at normal incidence, ${\upbeta }_{o} =0^\circ$, where ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{M}} }_{1,1} = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{{M}} }_{2,2}.$

Bragg reflections

The Nth-order Bragg reflection is caused by the resonant increase of ${{\textbf{E}}}^{(-N)}$ up to the amplitude of the major harmonic ${{\textbf{E}}}^{(0)}$ when ${a}_{x},{a}_{y}\approx \frac{N}{2}$ and $k\approx \frac{N}{2}$. To model this process, we derive the equations for ${{\textbf{E}}}^{(0)}$ and ${{\textbf{E}}}^{(-N)}$ by eliminating non-resonance harmonics ${{\textbf{E}}}^{(l)}$, $l\ne 0,-N$, from Equation 7:

$$\begin{gathered} \tilde{\textbf{M}}_{0} \left( 0 \right){\textbf{E}}^{\left( 0 \right)} + \tilde{\textbf{M}}_{ - N} \left( 0 \right){\textbf{E}}^{{\left( { - N} \right)}} = 0, \hfill \\ \tilde{\textbf{M}}_{N} \left( { - N} \right){\textbf{E}}^{\left( 0 \right)} + \tilde{\textbf{M}}_{0} \left( { - N} \right){\textbf{E}}^{{\left( { - N} \right)}} = 0, \hfill \\ \end{gathered}$$

(13)

where the resonance matrices $\tilde{\textbf{M}}_{j} \left( m \right)$ are the polynomial expansions in $\updelta$,

$$\tilde{\textbf{M}}_{j} \left( m \right) = {\textbf{M}}_{j} \left( m \right) - \sum\nolimits_{l \ne j,0} {{\textbf{M}}_{l} \left( m \right){\textbf{M}}_{0}^{ - 1} \left( {l + m} \right){\textbf{M}}_{j - l} \left( {l + m} \right) + O\left( {\updelta^{3} } \right)}.$$

(14)

The first term on the right-hand side of Equation 14 is dominant in the first, $N =1$, and the second, $N =2$, order Bragg reflections, and it is absent in all higher-order reflections, $N\ge 3$ (Equation 8). These higher-order reflections are caused by the indirect interaction between the resonant harmonics through the nonresonant ones and are described in subsequent terms on the right-hand side of Equation 14. To find the behavior of the four eigenmodes near the Nth order, the determinant of Equation 13 is evaluated into the fourth-order polynomial expansion in a small parameter ${\upmu }_{N} =k-\frac{N}{2}$,

$$\upmu_{N}^{4} - 2B_{N} \upmu_{N}^{2} + C_{N} = 0,$$

(15)

where ${B}_{N}$ and ${C}_{N}$ are functions of ${u}_{N} =u-{\left(\frac{N}{2}\right)}^{2}$, which change the sign in the Nth-order Bragg reflection region, whereas $v\propto {\updelta \upeta }^{2}$ (Equation 9), and ${b}_{n\xi }\propto {\updelta \upeta }^{n}$, $n =\mathrm{1,2}$ (Equation 5). The solutions of Equation 15 produce two evanescent modes when ${C}_{N}<0$ and all four eigenmodes when (1) ${D}_{N} ={B}_{N}^{2}-{C}_{N}<0$ or (2) ${B}_{N}<0$ and ${C}_{N}>0$. The results for the first four Bragg reflection orders are presented below.

First order, N = 1

For the first-order Bragg diffraction, Equation 15 has the coefficients

$$B_{1} = u_{1}^{2} + v^{2} - \frac{{\overline{b}_{1}^{2} }}{4}, C_{1} = \left( {u_{1}^{2} - v^{2} - \frac{{\overline{b}_{1}^{ 2} }}{4}} \right)^{2} \ge 0,$$

(16)

where

$$\overline{b}_{1} = \sqrt {b_{1x} b_{1y} } = \frac{{\updelta \upeta \sin \upbeta_{o} \sin 2\uptheta }}{{2\sqrt {\left( {1 + 2\updelta \cos^{2} \uptheta } \right)\left( {\cos^{2} \upbeta_{o} + 2\updelta \cos^{2} \uptheta } \right)} }},$$

(17)

and results in four eigenmodes with the wave vectors

$$k_{ \mp , \pm } = \frac{1}{2} \mp v \pm \sqrt {4u_{1}^{2} - \overline{b}_{1}^{2} }.$$

(18)

All four eigenmodes are evanescent with the same $\upalpha =\left|{\text{Im}}{k}_{\mp ,\pm }\right|$ in the region ${{u}_{1}^{r}<u}_{1}<{u}_{1}^{b}$, where $u_{1}^{b,r} = \pm \frac{{\overline{b}_{1} }}{2}$ are the blue and red edges of the Bragg reflection band, respectively. Thus, $\overline{b}_{1}$ determines both the width of the first-order Bragg reflection band $\Delta u_{1} = u_{1}^{b} - u_{1}^{r} = \overline{b}_{1}$ and its maximum $\upalpha_{{{\text{max}}}} = \overline{b}_{1}$ at the center, ${u}_{1} =0$. Since $\overline{b}_{1} \propto \tan \upbeta_{o} \sin 2\uptheta,$ the first-order Bragg reflection band (1) becomes narrower and weaker when ${\upbeta }_{o}$ decreases and completely disappears for the normal incidence and (2) reaches maximum when $\uptheta =45^\circ$ and disappears in the right-angle Ch, $\uptheta =90^\circ$, and in the unwound helicoid, $\uptheta =0^\circ$.

The incident from $z<0$ light generates the mode with ${k}_{-,+}$ and harmonics ${E}_{y}^{(0)}$ and ${E}_{x,z}^{(-1)}$, and mode with ${k}_{+,+}$ and harmonics ${E}_{x,z}^{(0)}$ and ${E}_{y}^{(-1)}$. Because the evanescent modes contain harmonics with crossed polarizations and have the same $\upalpha =\left|{\text{Im}}{k}_{\mp ,\pm }\right|$, the incident s-polarized wave reflects as the p–polarized one and vice versa, while the full reflectivity remains polarization independent.

To compare the model results with the experimental spectra presented below, the multiple order Bragg bands in Ch_OH and Ch (Figure 2e–g and Figure 6d) are shown in scaled coordinates ${{\widehat{u}}_{N} =u}_{N}/\updelta {\upeta }^{2}$ and $\widehat{\upalpha } =\upalpha /\updelta {\upeta }^{2}$ to make the plots more general because $v\propto \updelta {\upeta }^{2}$ and $\overline{b}_{2}\propto \updelta {\upeta }^{2}$ for the second order; for the first order, $\overline{b}_{1} \propto \updelta \upeta$ requires an additional factor $\upeta =\sqrt{{N}^{2}\,{+\,4u}_{N}}/{2n}_{\text{eff}}$ and $\overline{b}_{1} /\updelta \upeta^{2}$ has no singularity when ${\upbeta }_{o}\to 90^\circ$.

Figure 2

Multiple orders of Bragg reflection at Ch_OH. (a) Reflection from P, P/2, and P/3 observed simultaneously in the visible and near-infrared spectral regions; unpolarized light; planar cell, $d$ = 22.7 µm; angle of light incidence $\upbeta$ = 55°; $E$ = 0.7 V/μm. Polarization characteristics of reflections at (b) P, (c) P/2, and (d) P/3; spectra are presented for p–p, p–s, s–p, and s–s polarizations, where p–s and s–p states are overlap**; the first and second symbols indicate polarizations of the incident and reflected beams, respectively. The theoretically calculated dependencies of (e) the first-order and (f) the second-order Bragg bands of Ch_OH on the incident angle $\upbeta$ are shown in scaled coordinates ${{\widehat{u}}_{N} =u}_{N}/\updelta {\upeta }^{2}$. The upper parts of the panels show $\widehat{\upalpha } ={\text{Im}}\space{k}_{-,+}/\updelta \upeta^{2}$, which determines the reflection amplitudes of the Bragg bands for angle $\upbeta$ = 45° in experimental spectra (b) and (c). Dashed blue, green, and red lines correspond to s–s, s–p, and p–p polarizations, respectively. (g) The dependence of the second-order Bragg reflection bands on $\upbeta$ for a conventional Ch; the upper parts of the panels are calculated for $\upbeta = 70^\circ$ at which all three bands exist and show that the s–s and p–p bands switch sides as compared to the case of Ch_OH in panel (f).

Second order, N = 2

For the second-order Bragg reflection, the coefficients in biquadratic Equation 15 are

$$B_{2} = \frac{{2\left( {u_{2}^{2} + v^{2} } \right) - b_{2 + }^{2} }}{8},C_{2} = \frac{{\left( {u_{2}^{2} - v^{2} } \right)^{2} - \left( {b_{2 + } u_{2} + b_{2 - } v} \right)^{2} }}{16},$$

(19)

where ${b}_{2\pm } =\left({b}_{2y}\pm {b}_{2x}\right)/2$. The eigen wave vectors

$$k_{ \mp , \pm } = 1 \pm \sqrt {B_{2} \mp \sqrt {D_{2} } }$$

(20)

are evaluated using the standard analysis of a biquadratic equation; here,

$$D_{2} = B_{2}^{2} - C_{2} = \left[ {\left( {u_{2} v + b_{2 + } b_{2 - } } \right)^{2} - \left( {v^{2} - b_{2 + }^{2} } \right)\left( {b_{2 + }^{2} - b_{2 - }^{2} } \right)} \right]/4$$

(21)

is the discriminant of Equation 15.

The properties of eigenmodes are primarily controlled by the sign of ${C}_{2}$. Equation ${C}_{2} =0$ has four real solutions ${u}_{2-}^{-}<{u}_{2-}^{+}<{u}_{2+}^{-}<{u}_{2+}^{+}$,

$$u_{2 \mp }^{ \pm } = \mp \sqrt {\left( {v \pm b_{2 - } } \right)^{2} + b_{2x} b_{2y} } \pm b_{2 + },$$

(22)

presented by magenta, red, blue, and black lines, respectively, for half-pitch Bragg bands in Ch_OH and Ch (Figure 2f–g); thus, the entire range of ${u}_{2}$ splits into five regions with alternating signs of ${C}_{2}$. In the outer regions ${{(u}_{2}<u}_{2-}^{-})$ and ${(u}_{2}>{u}_{2+}^{+})$ where ${C}_{2}>0$, all wave vectors ${k}_{\mp ,\pm }$ (Equation 20) are real and represent the propagating modes; thus, Bragg reflection does not occur.

In the magenta–red $(u_{2 - }^{ - } < u_{2} < u_{2 - }^{ + } )$ and blue–black $(u_{2 + }^{ - } < u_{2} < u_{2 + }^{ + } )$ side regions, a negative ${C}_{2}$ results in a negative $B_{2} - \sqrt {D_{2} } = - \upalpha_{ - }^{2}$ and a complex ${k}_{-,\pm } =1\pm i {\upalpha }_{-}$ (Equation 20), while ${k}_{+,\pm }$ remain real. Thus, incident light exhibits the single-mode Bragg reflection bands in both regions, with the maxima at

$$u_{2 \mp }^{m} = \frac{1}{2}\left( {u_{2 \mp }^{ + } + u_{2 \mp }^{ - } } \right).$$

(23)

The width of the reflection bands is the same as the width of the corresponding regions $\Delta u_{2 \mp } = u_{2 \mp }^{ + } - u_{2 \mp }^{ - },$ top and bottom parts of Figure 2f, respectively. Both bands are caused by the same mode with ${k}_{-,+} =1+i {\upalpha }_{-}$. Under the condition $\left|v\right|>{b}_{2+}$ that is obeyed in Ch_OH when ${\upbeta }_{o}>\uptheta$ and in the right-angle Ch when ${\upbeta }_{o}>60^\circ$, this mode has linearly p-polarized harmonics $E_{x,z}^{\left( 0 \right)}$ and $E_{x,z}^{{\left( { - 1} \right)}}$ in the magenta–red region for Ch_OH (Figure 2f), and in the blue–black region for Ch (Figure 2g), respectively, whereas this mode has s-polarized harmonics ${E}_{y}^{(0)}$ and ${E}_{y}^{(-1)}$ in the alternative region. When ${\upbeta }_{o}$ decreases, the harmonics’ polarization in both modes transforms into an elliptical one with the same sign and further into the same circular polarization for the normal incidence, ${\upbeta }_{o} =0^\circ$, while the bands coalesce into the single band of the exact solution in both conventional right-handed Ch and Ch_OH.

The central red–blue region ${({u}_{2-}^{+}<{u}_{2}<u}_{2+}^{-})$ contains four areas. The area encircled by the green line corresponds to ${D}_{2}<0$ and determines the band similar to the first-order Bragg reflection band where all four eigenmodes have the same $\upalpha =\left|{\text{Im}}\space {k}_{\mp ,\pm }\right|$ and consist of the cross-polarized harmonics. The central band’s maximum position

$$u_{2c}^{m} = - \frac{{b_{2 + } b_{2 - } }}{v} \approx - \frac{{\updelta \upeta^{2} \left( {1 + \cos^{2} \upbeta_{o} } \right)\sin^{4} \uptheta }}{{4\left( {1 + 3\cos 2\uptheta } \right)}}$$

(24)

and its width

$$\Delta u_{2c} = \sqrt {b_{2x} b_{2y} \left( {1 - v^{ - 2} b_{2 + }^{2} } \right)} \approx \frac{1}{2}\updelta \upeta^{2} \cos \upbeta_{o} \sin^{2} \uptheta \sqrt {1 - \frac{{\sin^{4} \uptheta \left( {2 - \sin^{2} \upbeta_{o} } \right)}}{{\sin^{4} \upbeta_{o} \left( {1 + 3\cos 2\uptheta } \right)^{2} }}}$$

(25)

are defined by the roots of ${D}_{2} =0$ (Equation 21), and explain their dependencies on ${\upbeta }_{o}$ for Ch_OH (Figure 2f) and Ch (Figure 2g). Similar to the first-order Bragg reflection band, the incident s-polarized wave in this band reflects as the p-polarized one and vice versa.

In the area enclosed by red, blue, and green lines, all four eigenmodes are also evanescent because ${C}_{2}>0$, ${B}_{2}<0$, ${B}_{2}\mp \sqrt{{D}_{2}} =-{\upalpha }_{\mp }^{2}$ and ${k}_{\mp ,\pm } =1\pm i {\upalpha }_{\mp }$ (Equation 20) (Figure 2f and Figure 2g).

In the two remaining areas enclosed by red–green and blue–green lines in Figure 2f and  g, respectively, all wave vectors ${k}_{\mp ,\pm }$ (Equation 20) are real and represent the propagating modes.

Third order, N = 3

Bragg reflection of the third order occurs when ${a}_{x,y}\approx \frac{3}{2}$. The matrices

$$\tilde{\textbf{M}}_{ - 3} \left( 0 \right) = \tilde{\textbf{M}}_{3} \left( { - 3} \right) = \left( {\begin{array}{*{20}c} {\frac{1}{4}b_{1x} \left( {7b_{2y} - 12b_{2x} } \right)\upmu_{3} } & { - i\frac{3}{2}b_{1x} b_{2 - } } \\ {i\frac{3}{2}b_{1y} b_{2 - } } & {\frac{5}{4}b_{1x} b_{2y} \upmu_{3} } \\ \end{array} } \right)$$

(26)

control the interaction between the resonant harmonics ${\mathbf{E}}^{(0)}$ and ${\mathbf{E}}^{(-3)}$ (Equation 13) and are similar to the matrices $\tilde{\textbf{M}}_{ - 1} \left( 0 \right)$ and $\tilde{\textbf{M}}_{1} \left( { - 1} \right)$ in the first-order Bragg reflection. $\tilde{\textbf{M}}_{ - 3} \left( 0 \right)$ and $\tilde{\textbf{M}}_{3} \left( { - 3} \right)$ also have zero-value diagonal elements when ${\upmu }_{3} =0$ and generate the coefficients in Equation 15 that obey the condition $C_{3} \ge 0$,

$$B_{3} = \frac{{\tilde{u}_{3}^{2} + v_{3}^{2} - {\overline{b}}_{3}^{2} }}{9}, C_{3} = \frac{{\left( {\tilde{u}_{3}^{2} - v_{3}^{2} - {\overline{b}}_{3}^{2} } \right)^{2} }}{81} \ge 0,$$

(27)

where $\tilde{u}_{3} = u_{3} - \updelta u_{3},$ ${v}_{3}^{2} ={\left(v-2{b}_{1x}{b}_{1-}+\frac{{4b}_{2-}{b}_{2+}}{5}\right)}^{2}+{g}_{x}{g}_{y}{\left({b}_{1x}{b}_{1}+\frac{{2b}_{2-}{b}_{2}}{5}\right)}^{2}$, $\overline{b}_{3}^{2} = \frac{{9b_{1x} b_{1y} b_{2 - }^{2} }}{4},$ and $\updelta u_{3} = \frac{{4b_{2 + }^{2} }}{5} - b^{2}_{1x}- \frac{{7b_{1x} b_{1y} }}{16}.$ The four eigenmodes near the third-order Bragg reflection have the wave vectors

$$k_{ \pm , \pm } = \frac{3}{2} \pm \frac{{v_{3} }}{3} \pm \frac{1}{3}\sqrt {\tilde{u}_{3}^{2} - {\overline{b}}_{3}^{2} }$$

(28)

and are all evanescent when $\tilde{u}_{3}^{2} < \overline{b}_{3}^{2} .$ Similar to the first-order Bragg reflection, the evanescent modes contain harmonics with crossed polarizations; therefore, the incident p-mode reflects as the s-mode and vice versa.

The parameter $\updelta u_{3} = \frac{{4b_{2 + }^{2} }}{5} - b_{1x}^{2} -\frac{{7b_{1x}b_{1y} }}{16}$ determines the center of the Bragg peak, whereas

$$\overline{b}_{3} = \frac{{3\sqrt {b_{1x} b_{1y} } b_{2 - } }}{2} = \frac{{3\updelta^{2} \upeta^{3} \sin^{3} \upbeta_{o} \cos^{2} \upbeta_{o} \sin^{2} \uptheta \sin 2\uptheta }}{{8\sqrt {\left( {1 + 2\updelta \cos^{2} \uptheta } \right)^{3} \left( {\cos^{2} \upbeta_{o} + 2\updelta \cos^{2} \uptheta } \right)^{3} } }}$$

(29)

defines its maximum value ${\text{Im}}\space k_{ \pm , + } \left( {u_{3} = \Delta u_{3} } \right) = \frac{{\overline{b}_{3} }}{3}$ and its width $\Delta u_{3} = u_{3}^{b} - u_{3}^{r} = 2\overline{b}_{3},$ where $u_{3}^{b} = \updelta u_{3} + \overline{b}_{3}$ and $u_{3}^{r} = \updelta u_{3} - \overline{b}_{3}$ are the blue and the red edges of the band, respectively. Equation 29 for $\overline{b}_{3}$ demonstrates the absence of the third-order Bragg reflection for the normal incidence, consistent with the exact solution. It suggests that the experimental observation of the third-order Bragg reflection in Ch_OH is facilitated by a weak field (which implies a larger $\uptheta$) and by a large incidence angle β (Figure 2d).

Fourth order, N = 4

The Bragg reflection of the fourth order occurs when ${a}_{x,y}\approx 2$ and is very similar to the second order: the matrices $\tilde{\textbf{M}}_{ - 4} \left( 0 \right)$ and $\tilde{\textbf{M}}_{ 4} \left( { - 4} \right)$ control the interaction between the resonant harmonics ${{\textbf{E}}}^{(0)}$ and ${{\textbf{E}}}^{(-4)}$ (Equation 13) and are proportional to the second-order matrices ${{\textbf{M}}}_{\pm 2}$,

$$\tilde{\textbf{M}}_{ - 4} \left( 0 \right) = g_{4} {\textbf{M}}_{ - 2} ,\, \tilde{\textbf{M}}_{4} \left( { - 4} \right) = g_{4} {\textbf{M}}_{ + 2} ,$$

(30)

with the coefficient ${g}_{4} =\frac{\updelta {{\text{sin}}}^{2}{\upbeta }_{o}{{\text{sin}}}^{2}\uptheta \left({{\text{cos}}}^{2}{\upbeta }_{o}+2\updelta {{\text{cos}}}^{2}\uptheta \right)}{2\left[\left(1+\updelta {{\text{sin}}}^{2}\uptheta \right){{\text{cos}}}^{2}{\upbeta }_{o}+2\updelta {{\text{cos}}}^{2}\uptheta \right]\left[{{\text{cos}}}^{2}{\upbeta }_{o}+\updelta \left(1+{{\text{cos}}}^{2}\uptheta \right)\right]}$. Thus, the coefficients ${B}_{4}$ and ${C}_{4}$ in biquadratic Equation 15 are similar to the second-order coefficients ${B}_{2}$ and ${C}_{2},$

$$B_{4} = \frac{{2\left( {u_{4}^{2} + v^{2} } \right) - b_{4 + }^{2} }}{8}, C_{4} = \frac{{\left( {u_{4}^{2} - v^{2} } \right)^{2} - \left( {b_{4 + } u_{4} + b_{4 - } v} \right)^{2} }}{16},$$

(31)

where ${b}_{4\pm } ={g}_{4}{b}_{2\pm }$ and the eigenmodes for the fourth-order Bragg reflection have the same three-band structure with polarization characteristics described by Equations 19–25, in which the index 2 is substituted with 4. The strong dependence of the ${g}_{4}$ factor on the conical angle $\uptheta$ and the angle of incidence ${\upbeta }_{o}$ implies that the observation of the fourth-order Bragg reflection in Ch_OH with a small $\uptheta$ is difficult. As will be shown in the experimental part (Figure 6e), this peak is visible only when the field is weak (so that $\uptheta$ is not very small) and ${\upbeta }_{o}$ is large. The ${g}_{4}$ factor is responsible for the difference in the ${\upbeta }_{o}$ dependence of the fourth- and second-order reflections in both Ch_OH and Ch. In Figure 2g, which describes the second-order Bragg reflection of the conventional Ch at ${P}_{0}/2$, the decrease of ${\upbeta }_{o}$ to zero produces a single-mode band, which corresponds to the exact solution. In contrast, the decrease of ${\upbeta }_{o}$ to zero in the case of the fourth order ${P}_{0}/4$ reflection of Ch results in a disappearance of all three bands (see Figure 6d).

One would expect that all orders of Bragg reflection should have three bands corresponding to the resonant interaction of p–p, s–p (p–s), and s–s modes. However, for odd N, the matrices ${{\tilde{\textbf{M}}} }_{ - N} \left( 0 \right)$ and ${{\tilde{\textbf{M}}} }_{N} \left( { - N} \right)$ in Equation 13 have zero-value diagonal elements when ${\text{Re}}\space k =\frac{N}{2}$, providing the condition ${C}_{N}\ge 0$ and making p–p and s–s bands in the odd order Bragg reflections nonexistent.

Experimental results

Multiple bands of reflection

According to theory, Bragg reflection of the $N$th order at the wavelength ${\uplambda }_{P/N}\approx \frac{{n}_{o}P {\text{cos}}{\upbeta }_{o}}{N}$ appears whenever ${a}_{x},{a}_{y}\approx \frac{N}{2}$, where the angle ${\upbeta }_{o}$ of light propagation in the liquid crystal is calculated using Snell’s Law, ${\upbeta }_{o} = {\text{arcsin}}\left(\frac{{n}_{g}{\text{sin}}\upbeta }{{n}_{o}}\right)$, and the angle $\upbeta$ of light incidence is measured from the normal to the Ch_OH cell (Figure 1f and g). The reflection spectra are measured for different values of $\upbeta$ and the electric field $E$; the field tunes the heliconical angle $\uptheta$ and the pitch $P$ (Figure 1c and d), and shifts reflection bands corresponding to the full pitch $P$ and its fractions $P/2$, $P/3$, and $P/4$. The reflections at $P$, $P$/2, and $P$/3 are measured in the Ch_OH dopped with 4 wt% of the chiral additive (abbreviated as M4), and reflection at $P$/4 is characterized using the Ch_OH with 3 wt% of the chiral dopant (M3).

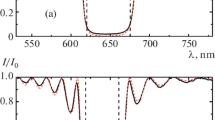
The experimental spectrum in Figure 2a shows three orders of Bragg reflection, $N =1, 2,\,\mathrm{ and} \,3$, of an unpolarized light that im**es obliquely, β = 55°, at the Ch_OH stabilized by the field, E  = 0.7 V/μm. In addition to the conventional reflection at $P$/2, one observes a reflection band at P and a peculiar reflection at $P$/3. The $P$, $P$/2, and $P$/3 bands are well separated from each other. The $P$ -band centered at ${\uplambda }_{P}$ = 930 nm, and the P/3 band at ${\uplambda }_{P/3}$ = 360 nm both represent a single maximum, while the reflection at P/2 exhibits three peaks. The ratio ${\uplambda }_{P}/{\uplambda }_{P/3}$ = 2.58 is different from 3 because of the dispersion of refractive indices (Supplementary information [SI] Figure S1). The reflection at $P$/4 is discussed later since this band is in the UV region for a given electric field and cannot be shown in Figure 2.

Polarization properties

Electric control of the pitch allows one to shift the reflection bands and explore their polarization properties in a convenient part of the spectrum (Figure 2b–d). In agreement with the theory, the reflection band at $P$/2 is a triplet (Equations 23–24 and Figure 2f), while reflections at $P$ (Equation 18 and Figure 2e) and $P$/3 (Equation 29) are single peaks. When the incident light is p-polarized, its reflection at $P$ and $P$/3 is s-polarized, and vice versa, an s-polarized incident ray changes into a p-polarized one (Figure 2b, d). The $P$/2 band is more complicated, with three maxima (Figure 2c), as expected from Figure 2f. The central peak exhibits a conversion of the p (s) polarization of the incident light into an s (p) polarization of the reflected light, similar to the singlet peaks of reflection at P and $P$/3. The blueshifted peak of the $P$/2 triplet shows a strong reflection of the s-polarized light into a similarly s-polarized light, while the redshifted maximum corresponds to the reflection of p-polarized light into a similarly p-polarized beam (Figure 2c).

All bands in Figure 2b–d show secondary reflections, such as finite s–s reflection outside the Bragg bands, and satellite peaks in the second-order Bragg reflection in Figure 2c. The weak s–s reflection in Figure 2b–d is caused by reflection at the electrodes at both glass plates. The p–p reflection is much weaker at large incidence angles as it is close to the Brewster condition. As a result, the s–s reflection is always larger than the p–p reflection outside the strong reflection band p–s in Figure 2b and d. Inside the p–s band, the s–s and p–p reflections are weaker than the ones outside the band because the contribution from the opposite substrate is eliminated.

Figure 2c shows the satellite s–s and p–p peaks located under the main p–s peak. This result is unusual because these peaks cannot be caused by an ideal Ch_OH structure. We attribute the effect to the fact that the subsurface structure (the conical angle and the pitch) of the Ch_OH is different from an ideal helicoid because of the surface anchoring.²⁴ As a result, the incident light becomes elliptically polarized, which means that the p-component of the incident light reflects as the s-component and vice versa. This effect brings about the additional peaks such as the s–s and p–p reflections underneath the p–s band in Figure 2c. A similar effect is the appearance of a weak p–s and s–p reflections under the s–s peak and even weaker reflections under the p–p band in Figure 2c.

Heliconical angle ${\varvec{\uptheta}}$ and pitch ${\varvec{P}}$ of the Ch_OH

The structure of the Bragg reflection at $P$/2 allows one to determine the heliconical angle $\uptheta$ and the pitch $P$ directly from spectra, such as one in Figure 2c. The peak wavelengths ${\uplambda }_{P/2}$ with p–p, p–s, and s–s polarization states (Figure 3a) are substituted into Equations 23 and 24 to calculate $\uptheta$ and $P$ (Figure 3b–c, respectively). The peak wavelength ${\uplambda }_{P/2}$ at a given polarization is determined by measuring the peak’s bandwidth at its half-amplitude and defining the middle coordinate of the bandwidth. We use notations with superscripts to identify the state of polarization of the incident and reflected beams; for example, ${\uplambda }_{P/2}^{{\text{ps}}}$ refers to a p-polarized incident light that is reflected as an s-polarized beam. The wavelength ${\uplambda }_{P/2}^{{\text{ps}}}$ = ${\uplambda }_{P/2}^{{\text{sp}}}$ corresponds to the central peak in the triplet (Equation 24). The angle $\uptheta$ and the pitch $P$ are determined from the equations

$$\uplambda_{P/2}^{\upsigma } = n_{o\upsigma } P\sqrt {U_{\upsigma } - \Delta U_{\upsigma } },$$

(32)

by solving for the pairs $\left\{{\uplambda }_{P/2}^{{\text{pp}}}, {\uplambda }_{P/2}^{{\text{ss}}}\right\},$ $\left\{{\uplambda }_{P/2}^{{\text{pp}}}, {\uplambda }_{P/2}^{{\text{ps}}}\right\}$, and $\left\{{\uplambda }_{P/2}^{{\text{ps}}}, {\uplambda }_{P/2}^{{\text{ss}}}\right\}$, where $\upsigma ={\text{pp}},\mathrm{ ps},\mathrm{ ss}$,

$$U_{\upsigma } = \frac{{\left( {\cos^{2} \upbeta_{o} \left( {1 + \updelta_{\upsigma } \sin^{2} \uptheta } \right) + 2\updelta_{\upsigma } \cos^{2} \uptheta } \right)}}{{2\left( {1 + 2\updelta_{\upsigma } \cos^{2} \uptheta } \right)}} + \frac{{\cos^{2} \upbeta_{o} \left( {\cos^{2} \upbeta_{o} + \updelta_{\upsigma } + \updelta_{\upsigma } \cos^{2} \uptheta } \right)}}{{2\left( {\cos^{2} \upbeta_{o} + 2\updelta_{\upsigma } \cos^{2} \uptheta } \right)}},$$

$$\Delta U_{\text{ps}} = - \frac{{ {{\updelta }} _{\text{ps}} \left( {1 + \cos^{2} \upbeta_{o} } \right)\sin^{4} \uptheta }}{{\left( {16 - 24\sin^{2} \uptheta } \right)}},$$

and for p–p and s–s polarizations,

$$\Delta U_{\upsigma } = \pm \frac{{\updelta_{\upsigma } }}{8}\left( {\sqrt {8 \sin^{4} \upbeta_{o} \cos^{2} \uptheta \left( {2 - 3\sin^{2} \uptheta } \right) + \left( {1 + \cos^{2} \upbeta_{o} } \right)^{2} \sin^{4} \uptheta } + \sqrt {8 \sin^{4} \upbeta_{o} \cos 2\uptheta \left( {2 - 3\sin^{2} \uptheta } \right) + \left( {1 + \cos^{2} \upbeta_{o} } \right)^{2} \sin^{4} \uptheta } } \right),$$

with + and − corresponding to pp and ss peak wavelengths, respectively. Here, $\updelta_{\upsigma } = \frac{{n_{e\upsigma }^{2} - n_{o\upsigma }^{2} }}{{2n_{o\upsigma }^{2} }},$ where refractive indices $n_{o\upsigma } = n_{o} \left( {\uplambda_{P/2}^{\upsigma } } \right)$ and $n_{e\upsigma } = n_{e} \left( {\uplambda_{P/2}^{\upsigma } } \right)$ are chosen for the corresponding peak wavelength. The values of $\uptheta$ determined from Equation 32 for pairs $\left\{ {\uplambda_{P/2}^{{{\text{pp}}}} ,\uplambda_{P/2}^{{{\text{ss}}}} } \right\},$ $\left\{ {\uplambda_{P/2}^{{{\text{pp}}}} ,\uplambda_{P/2}^{{{\text{ps}}}} } \right\}$ and $\left\{{\uplambda }_{P/2}^{{\text{ps}}}, {\uplambda }_{P/2}^{{\text{ss}}}\right\}$ are in a good agreement with each other (Figure 3b). This result is remarkable since $\uptheta$ is determined from the difference in the two peaks’ positions and is thus sensitive to how accurately these are measured (Figure 2c). The pairs $\left\{ {\uplambda_{P/2}^{{{\text{pp}}}} ,\uplambda_{P/2}^{{{\text{ss}}}} } \right\}$ with the largest peak separation, and $\left\{{\uplambda }_{P/2}^{{\text{pp}}}, {\uplambda }_{P/2}^{{\text{ps}}}\right\}$, where the peaks are the narrowest and of the most symmetric shape, provide a more reliable $\uptheta$ than $\left\{ {\uplambda_{P/2}^{{{\text{ps}}}} ,\uplambda_{P/2}^{{{\text{ss}}}} } \right\},$ in which case the wide asymmetric shape of ${\uplambda }_{P/2}^{{\text{ss}}}$ is the probable source of deviations seen in Figure 3b. The determination of pitch $P$ is robust, yielding practically the same values when measured from all three pairs $\left\{ {\uplambda_{P/2}^{{{\text{pp}}}} ,\uplambda_{P/2}^{{{\text{ss}}}} } \right\},$ $\left\{ {\uplambda_{P/2}^{{{\text{pp}}}} ,\uplambda_{P/2}^{{{\text{ps}}}} } \right\},$ and $\left\{ {\uplambda_{P/2}^{{{\text{ps}}}} ,\uplambda_{P/2}^{{{\text{ss}}}} } \right\}$ (Figure 3c).

Figure 3

Electrically tunable (a) wavelength ${\uplambda }_{P/2}$, (b) heliconical angle $\uptheta$, (c) pitch $P$ (left vertical axis) and the ratio $\widetilde{N} =d/P$ (right vertical axis) measured in the planar cell, d  = 22.7 µm, at an angle of incidence β = 40°. In (b–c), the values of $\uptheta$ and $P$ are determined from Equation 32 solving for the pairs $\left\{{\uplambda }_{P/2}^{{\text{pp}}}, {\uplambda }_{P/2}^{{\text{ss}}}\right\},$ $\left\{{\uplambda }_{P/2}^{{\text{pp}}}, {\uplambda }_{P/2}^{{\text{ps}}}\right\}$, and $\left\{{\uplambda }_{P/2}^{{\text{ps}}}, {\uplambda }_{P/2}^{{\text{ss}}}\right\}$. (d) The change in number of Ch pseudolayers $\widetilde{\Delta }$ is close to the integer at low fields and deviates from the integer at stronger fields.

Figure 3d shows how the change of the electric field changes the number of the cholesteric pseudolayers. The parameter $\tilde{\Delta }_{i + 1} = \tilde{N}\left( {E_{i} } \right) - \tilde{N}\left( {E_{i + 1} } \right)$ represents the difference between the number of pseudolayers defined experimentally as $\widetilde{N} =d/P$ at two close values of the applied electric field ${E}_{i}$ and ${E}_{i+1}.$ This parameter should be an integer if the change of the structure occurs by an insertion of a full period of the Ch_OH structure. However, the experiment shows that this parameter is not always exactly integer. The reason is in the complex $z$-dependence of the structure, with the ideal heliconical deformation distorted near the substrates, as explained previously.²⁴ The field dependencies of $P$ and $\uptheta$ in Figure 3 are obtained from Bragg reflection and therefore represent the values ${P}_{\text{bulk}}$ and ${\uptheta }_{\text{bulk}}$ in the homogeneous bulk region of the cell; these parameters are different near the substrates. The true change of the number of pseudolayers is shown in Figure 3d as a parameter ${\Delta }_{i+1}$ defined as the integer closest to ${\widetilde{\Delta }}_{i+1}$. When $E<0.9\,\mathrm{ V}/\mathrm{\upmu m}$, the two parameters practically coincide, $0<\widetilde{\Delta }-\Delta \ll 1$ and the number of pseudolayers changes by 1; for higher fields, when the pitch is small, the number of added pseudolayers is often higher, $\Delta =\mathrm{2,3}$, and the difference $\widetilde{\Delta }-\Delta$ becomes substantial. The reason for this high-field behavior is that the decrease of $P$ amplifies the effect of the inhomogeneous subsurface layers.

Equation 32 represents an independent and direct approach to measure $\uptheta$ and $P$ from spectra. A different approach, based on the elastic and dielectric properties of the Ch_OH, was proposed earlier,²⁰ in which $P$ and $\uptheta$ are theoretically predicted (assuming they do not change along the normal to the cell) as:²⁰

$$P = \frac{{\upkappa E_{\text{NC}} P_{0} }}{E} = \frac{2\uppi }{E}\sqrt {\frac{{K_{33} }}{{\upvarepsilon_{0} \Delta \upvarepsilon }}},$$

(33)

$$\sin ^{2} {\text{ }}\uptheta = \frac{\upkappa }{{1 - \upkappa }}\left( {\frac{{E_{{NC}} }}{E} - 1} \right),$$

(34)

where $\upkappa ={K}_{33}/{K}_{22}{, E}_{\text{NC}} ={2\uppi K}_{22}/ {P}_{0}\sqrt{{\upvarepsilon }_{0}\Delta \upvarepsilon {K}_{33}}$ is a critical field at which the Ch_OH transforms into an unwound state with θ  = 0 ( Figure 1e). Therefore, one can combine the spectral (Equation 32) and the elasto-dielectric (Equations 33–34) approaches for the same cell and determine, in addition to $\uptheta$ and $P$, also other parameters, such as $\upkappa$ and $\frac{{K_{33} }}{\Delta \upvarepsilon }.$

Electric-field tunability

The unique feature of the Ch_OH $P$-band is that it produces a total reflection of obliquely incident light and that the wavelength ${\uplambda }_{P}$ of this reflection is tunable in a very broad range, for example, from 400 to 700 nm in Figure 4a, without diminishing its 100% efficiency. Both ${\uplambda }_{P}$ and the bandwidth ${\Delta \uplambda }_{P}$ decrease at higher fields (Figure 4b), since $P$ and $\uptheta$ both decrease, as expected from Equations 33 and 34. The electric-field dependencies in Figure 4b are measured for a p-polarized incident light; the reflected beam is s-polarized. The data are ingood agreement with the theory; peak wavelengths at the full pitch $P$ (N  = 1) satisfy the condition $\left({a}_{x}^{2}+{a}_{y}^{2}\right)$ = $\frac{1}{2}$ (Equation 15), where ${a}_{x}$ and ${a}_{y}$ are analytical expressions in Equation 5 with material parameters ${P}_{0}$, ${E}_{\text{NC}}$, and $\upkappa$, measured previously³³ (Figure 4b). The reflection band at $P$/3 shows a similar tunability by the electric field (Figure 4c). To observe the $P$/3 band in the visible range, the electric field is lowered, which increases the pitch. The electric-field dependency of the spectral position of the $P$/3 band is similar to that of the $P$-band; the peak wavelength ${\uplambda }_{P/3}$ and the bandwidth $\Delta \uplambda_{P/3}$ both decrease with the field (Figure 4d). Similarly to $\uplambda_{P}$, the $\uplambda_{P/3}$ data are in good agreement with the theory (N  = 3) ( Figure 4d). Note that the dependencies in Figure 4c have been measured in thick cells with a hybrid alignment in order to enhance the intensity of the  $P/3$ band (Equation 29) and to change the pitch continuously.

Figure 4

Electrically tunable reflection of light at (a) the Ch_OH pitch P and (c) one-third of the pitch P/3; the root-mean-square amplitudes of the field are indicated at the top of some bands. (b) Electric-field dependency of the reflection maximum ${\uplambda }_{P}$ and the bandwidth $\Delta {\uplambda }_{P}$; planar cell, d  = 22.7 µm; and angle of light incidence β = 45°. (d) Similar E-field dependency of ${\uplambda }_{P/3}$ and $\Delta {\uplambda }_{P/3}$; hybrid aligned cell, d  = 49.2 µm; β  = 50°. In (b, d), the data are fitted to the theory using values of $\uptheta$ and $P$ determined from Equation 32.

Dependence on the incident angle

Figure 5 shows that the wavelength of the Bragg peak for $P$ and $P$/3 bands could be controlled by the angle of light incidence $\upbeta$. A higher β causes blueshifts of the reflection wavelength since $\uplambda_{P} , \uplambda_{P/3} \propto \cos \upbeta$ (Figure 5a). At a fixed field, $E{\text{ }} = {\text{ }}1.1{\text{ V/m}},$ when $\upbeta$ increases from 30$^\circ$ to 58$^\circ$, the total reflection peak changes from about 610 nm to 450 nm, while its bandwidth increases (Figure 5a–b). The $P/3$ reflection band shows a similar blueshift when $\upbeta$ increases (Figure 5c). The experimental data are well fitted with the theoretical model with the parameters indicated in Figure 5 caption.

Figure 5

Control of peak wavelength by the angle of light incidence β: (a) Spectra of reflection at the full pitch $P$; the angle β is shown above the Bragg peaks; E  = 1.1 V/μm. (b) Wavelength ${\uplambda }_{P}$ and bandwidth ${\Delta \uplambda }_{P}$ of reflection at the full pitch $P$ versus β; (c) Similarly, the reflection at $P$/3 versus β is shown for E  = 0.79 V/μm (filled diamonds) and E  = 0.83 V/μm (empty squares). In (b, c), the data are fitted to the theory using material parameters ${P}_{0}$ = 1.7 µm, ${E}_{\text{NC}}$ = 4.7 V/μm, and $\upkappa =$ 0.03 measured previously.³³

Even order Bragg diffraction peaks

Triplet reflections at the half of Ch_OH pitch $(P$/2) (Figure 2c) and at the quarter of Ch pitch $({P}_{0}$/4) (Figure 6a) are similar. The central peak in both the Ch and Ch_OH triplets corresponds to the reflection that alters the polarization of light: if the incident light is p-polarized, the reflected beam is s-polarized and vice versa. The lateral peaks preserve the polarization of the incident beams. An important difference is that in Ch_OH, the lateral peak corresponding to the p–p reflection is located on the red side of the band (Figure 2c), while in the Ch case, the p–p peak is blueshifted (Figure 6a). The s–s peaks show a complementary behavior, being blueshifted in Ch_OH and redshifted in Ch. The effect is caused by the fact that spatially averaged Ch_OH is a positive uniaxial birefringent material, whereas Ch is a negative one, with the optic axis in both cases being along the twist axis (Equation 9, Figures 2f and 6d).

Figure 6

Bragg reflection at one-quarter of a pitch in Ch and Ch_OH: (a) Reflection at ${P}_{0}$/4 in Ch measured in M4. The spectra are presented for p–p, p–s, s–p, and s–s polarizations, where p–s and s–p states are overlap**; the first and second symbols indicate polarizations of the incident and reflected beams, respectively. The swap in polarization characteristics of Ch_OH and Ch is due to the difference between the effective refractive indices as illustrated in (b) and (c). Note the redshift of the p–p polarization away from the central peak in the Ch_OH (Figure 2c), and its blueshift in the Ch (Figure 6a). (d) The theoretically calculated dependency of the fourth-order Bragg band of a conventional Ch on the incident angle $\upbeta$. The upper parts of the panel show $\widehat{\upalpha } ={\text{Im}}\space {k}_{-,+}/\updelta \upeta^{2}$, which determines the amplitudes of the Bragg bands for $\upbeta$ = 65° (the same as the experimental $\upbeta$ in a). Dashed blue, green, and red lines correspond to s–s, s–p, and p–p polarizations, respectively; note that the theoretical bands are less symmetric and narrower than the experimental one; the features can be explained by an increased birefringence in the blue part of the spectrum and by director fluctuations (“noise”). (e) Bragg reflection of the fourth order $P$/4 in Ch_OH measured in M3; p–s polarization; planar cell, d = 16.2 µm; β = 52.5°; and E = 0.3 V/μm.

Observation of the $P/4$ band in Ch_OH is more difficult than in Ch because its intensity is very low, $\propto g_{4} b_{2} \propto \sin^{4} \uptheta$ (Equations 5 and 30). The $P$/4 band is observed in a planar cell, d  = 16.2 µm, filled with M3 (which yields a higher pitch) at $\upbeta$ = 52.5° (Figure 6e). The reflection at $P$/4 is caused by double scattering at the $P/2$. The peak wavelengths $\uplambda_{P/4}^{ps}$ are in good agreement with the calculated fourth Bragg order, in which the central peak of $P$/4 satisfies the condition $\left({a}_{x}^{2}+{a}_{y}^{2}\right)$ = 8 when $N$ = 4 (Equations 5 and 15). Due to low reflection intensity, polarization properties of the $P/4$ band are difficult to analyze.

Conclusion

We demonstrate that a single thin sandwich-type cell filled with an oblique helicoidal Ch_OH and acted upon by an electric field enables total reflection of obliquely incident light, which is tunable in a very broad spectral range, from ultraviolet to infrared. In a particular example in Figure 4a, the tunable range is from 400 to 700 nm. As demonstrated recently, a single cell filled with a Ch_OH material could yield electric tunability of the reflected structural color from some short wavelength $\uplambda$ all the way up to the longest wavelength ~20 $\uplambda$.³³ The tunable total reflection of obliquely incident light is associated with the period $P$ of Ch_OH. The electric field applied parallel to the heliconical axis of Ch_OH tunes the value of $P$ but does not change the single-mode character of the refractive-index modulation, which explains why the efficiency of reflection maintains its 100% value in a broad spectral range (Figure 4a). This 100% reflection is observed for any polarization of incident light.

In addition to the 100% reflection at $P$, the Ch_OH shows multiple orders of Bragg reflection, corresponding to $P/2$, $P/3$, and $P/4$. The $P/3$ and $P/4$ reflections are associated with the multiple scattering events at $P$ and $P/2$. Both theoretical model and experiment establish polarization patterns of the reflections, which are triplets in the case of the $P/2$ and $P/4$ bands and singlets in the $P$ and $P/3$ cases. The model allows one to extract the material parameters such as the heliconical angle $\uptheta$ and the pitch $P$ directly from the triplet structure of the $P/2$ band (Figure 3a–c). The knowledge of these two parameters allows one to determine the elastic constants of twist ${K}_{22}$ and bend ${K}_{33}$ using Equations 33–34 and optical spectra, without the need to resort to the measurements of the unwinding electric field ${E}_{\text{NC}}$.

Total reflection occurs when all four eigenmodes are evanescent and the wave vectors are complex. The most favorable conditions for the total reflection are created in the first-order Bragg reflection band that exists for oblique light incidence in the Ch_OH (Figure 2b, e), but does not exist in the right-angle Ch. This band exists for any incidence angle except for normal incidence (${\upbeta }_{o} =0$). It exhibits features useful for applications. Namely, the polarization of reflected light is orthogonal to the polarization of the incident light. Such a feature could be useful to eliminate noise reflection, which typically preserves the state of polarization. The coefficient of reflection does not depend on the polarization of the incident light and remains the same for linearly, circularly, or unpolarized incident light. The strong reflectivity is achieved for thin, 20–40 $\upmu \mathrm{m}$, samples thanks to the large effective amplitude $\overline{b}_{1}$ of optical tensor modulation.

The demonstrated total reflection of obliquely incident light of an arbitrary state of polarization and its broad tunability by an electric field suggest that Ch_OH materials will find applications in dynamic tunable optical and photonic devices. Among many advantages that they offer is the simplicity of construction and operation: a relatively thin (20–40 $\upmu \mathrm{m}$) layer of a Ch_OH sandwiched between two plates with planar transparent electrodes is already a device capable of extraordinary broad multispectral tunability.

Materials and methods

Ch_OH materials

A room-temperature nematic (N) LC precursor is formulated using flexible dimers 1′′,7′′-bis(4-cyanobiphenyl-4′-yl)heptane (CB7CB), 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl)hexane (CB6OCB) (both purchased from SYNTHON Chemicals GmbH & Co. KG), and a rod-like mesogen pentyl cyanobiphenyl (5CB) (EM Industries), in the weight proportion 5CB:CB7CB:CB6OCB  = 52:31:17. Upon cooling, the N mixture shows the phase diagram N_TB (17.4°C) N (78°C) I, where N_TB is the twist-bend nematic.^{\({N}_{{\text{TB}}}^{*}\) (17.1°C) Ch (65.0°C) I and ${N}_{{\text{TB}}}^{*}$ (15.5°C) Ch (66.3°C) I, respectively. Here, ${N}_{{\text{TB}}}^{*}$ is the chiral analog of the twist-bend nematic.45,46,47,48,49} The phase diagram is measured on cooling using Linkam hot stage equipped with the PE94 temperature controller (both Linkam Scientific) and EHEIM Professional-3 cooling system (EHEIM GmbH & Co. KG). The spectra at Ch_OH are measured without the hot plate at room temperatures, 19–20.5°C, with the accuracy ±0.2°C.

Cells with preset surface alignment

Two types of flat sandwich cells are studied, with the planar and hybrid²⁶ anchoring of the local director at the bounding surfaces. In planar cells, the Ch_OH structure adjusts its pitch slightly in order to comply with the boundary conditions. In hybrid aligned cells, one substrate yields a planar alignment, while the other produces a homeotropic alignment. The homeotropic substrate helps to tune the structure in a continuous manner since it imposes no in-plane axis for the director $\widehat{{\textbf{n}}}$. Planar cells with indium tin oxide (ITO) electrodes and gap thicknesses d  = (16–52) µm were either purchased from E.H.C. Co, Japan, or assembled in the laboratory. Planar alignment is achieved by a rubbed layer of polyimide PI2555 (Nissan Chemicals, Ltd.). Homeotropic substrates are prepared in the laboratory using the technique developed by Young-Ki Kim at Kent State.^50,51 The reactive mesogen RM257 is mixed with the homeotropic aligning agent SE5661 and doped with the UV photo-initiator Irgacure 651, in weight proportion SE5661:RM257:Irgacure 651 = 96.7:3:0.3. The mixture is spin-coated onto an ITO glass substrate and baked at 170°C for 1 h. The substrates are then irradiated with UV light (365 nm) for 90 min.^50,51 The cell thickness is set by spherical spacers mixed with UV-curable adhesive NOA68 (Norland Products, Inc.) and measured using a Lambda 18 UV/VIS spectrometer (PerkinElmer, Inc.). The cells are filled with the Ch_OH mixture in the isotropic phase and slowly cooled down at the rate 0.2°C /min to room temperature.

Electric-field control of the structure

To create the Ch_OH state, an AC field with a frequency 3 kHz is applied to the ITO electrodes at the bounding plates using a Keithley 3390 waveform function generator (Keithley Instruments) and a wideband Krohn-Hite 7602M amplifier (Krohn-Hite Co.) (Figure 1g). The field ${\textbf{E}}$ establishes the Ch_OH state with a helicoidal axis $\widehat{{\textbf{h}}}$ parallel to itself, $\widehat{{\textbf{h}}}||{\textbf{E}}$ (Figure 1c–d); the Ch_OH pitch P changes in a broad range in response to the changing amplitude of ${\textbf{E}}$.^20,21

Spectral measurements at an oblique incidence of light

The scheme of the experimental setup is shown in Figure 1f. The fiber-optics setup is based on a rotating goniometer stage (Euromex Holland), and optical spectra are measured using a tungsten halogen light source LS-1 with a working range 350–2000 nm and a USB2000 VIS–NIR spectrometer (both Ocean Optics, Inc.). Polarization of the incident and reflected (or transmitted) beams is set by a pair of linear wire-grid polarizers (Thorlabs, Inc.) placed along the optical path at the exit from the fiber connected to the light source and at the entrance to the fiber connected to the USB2000 detector. The incident ray is p-polarized when its electric field E_p oscillates in the plane of incidence xz and s-polarized when the electric field E_s is perpendicular to it. The Ch_OH cell is mounted in the center of the goniometer stage, and the angle of light incidence $\upbeta$ is measured from the normal $\widehat{\mathbf{z}}$ to the Ch_OH cell with an accuracy better than 0.25 degrees. The Ch_OH cell is sandwiched between two semicylindrical prisms (N-BK7 glass, n_p  = 1.518 at 547 nm, Thorlabs, Inc.). A Cargille matching liquid with the refractive index n  = 1.516 (at 600 nm) fills the gaps between the cell substrates and prisms to reduce the reflection losses. The semicylindrical prisms allow one to measure light reflection in a broad angular range and assure that the angle of light incidence from the glass is the same as the incidence angle from the air: ${\upbeta }_{g}{ =\upbeta }_{\text{air}}\equiv \upbeta$. Optical spectra are normalized with respect to the intensity of light ${I}_{0}$ passed through the Ch_OH cell in the transmission mode when the structure is unwound by a high applied field $E$ = 7 V/μm; this value exceeds the critical field ${E}_{\text{NC}}$ of unwinding the Ch_OH into the N state with the director $\widehat{{\bf{n}}}$ along the field (Figure 1e). ${E}_{\text{NC}}$ is measured by the capacitance method described previously.³³ Reflection spectra are measured at $E<{E}_{\text{NC}}$, when the material adopts the heliconical Ch_OH state (Figure 1c–d). The reflection coefficient is calculated as $R[\%] =\frac{{I}_{R} }{{I}_{0}}\times 100\%$, where ${I}_{R}$ is the intensity of light reflected from the Ch_OH.