SpringerLink
Log in

Error Analysis of Nonlinear Time Fractional Mobile/Immobile Advection-Diffusion Equation with Weakly Singular Solutions

  • Research Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

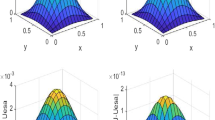
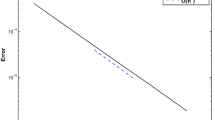
In this paper, a weighted and shifted Grünwald-Letnikov difference (WSGD) Legendre spectral method is proposed to solve the two-dimensional nonlinear time fractional mobile/immobile advection-dispersion equation. We introduce the correction method to deal with the singularity in time, and the stability and convergence analysis are proven. In the numerical implementation, a fast method is applied based on a globally uniform approximation of the trapezoidal rule for the integral on the real line to decrease the memory requirement and computational cost. The memory requirement and computational cost are O(Q) and O(QK), respectively, where K is the number of the final time step and Q is the number of quadrature points used in the trapezoidal rule. Some numerical experiments are given to confirm our theoretical analysis and the effectiveness of the presented methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. Banjai, M. López-Fernández, Efficient high order algorithms for fractional integrals and fractional differential equations. Numer. Math. 141, No 2 (2019), 289–317; 10.1007/s00211-018-1004-0.

    Article  MathSciNet  Google Scholar 

  2. D.A. Benson, M. M. Meerschaert, A simple and efficient random walk solution of multi-rate mobile/immobile mass transport equations. Adv. Water. Resources 32 (2009), 532–539; 10.1016/j.advwatres.2009.01.002.

    Article  Google Scholar 

  3. F. Chen, J. Shen, H. J. Yu, A new spectral element method for pricing European options under the Black-Scholes and Merton jump diffusion models. J. Sci. Comput. 52 (2012), 499–518; 10.1007/s10915-011-9556-5.

    Article  MathSciNet  Google Scholar 

  4. K. Diethelm, The Analysis of Fractional Differential Equations. Springer-Verlag, Berlin (2010).

    Book  Google Scholar 

  5. K. Diethelm, J. M. Ford, N. J. Ford, M. Weilbeer, Pitfalls in fast numerical solvers for fractional differential equations. J. Comput. Appl. Math. 186, No 2 (2006), 482–503; 10.1016/j.cam.2005.03.023.

    Article  MathSciNet  Google Scholar 

  6. W. Fan, F. Liu, X. Jiang, I. Turner, A novel unstructured mesh finite element method for solving the time-space fractional wave equation on a two-dimensional irregular convex domain. Fract. Calc. Appl. Anal. 20, No 2 (2017), 352–383; 10.1515/fca-2017-0019; https://www.degruyter.com/view/journals/fca/20/2/fca.20.issue-2.xml.

    Article  MathSciNet  Google Scholar 

  7. L. Feng, F. Liu, I. Turner, L. Zheng, Novel numerical analysis of multi-term time fractional viscoelastic non-Newtonian fluid models for simulating unsteady and MHD and Couette flow of a generalized Oldroyd-B fluid. Fract. Calc. Appl. Anal. 21, No 4 (2018), 867–868; 10.1515/fca-2018-0058; https://www.degruyter.com/view/journals/fca/21/4/fca.21.issue-4.xml.

    Article  MathSciNet  Google Scholar 

  8. L. Galeone, R. Garrappa, Fractional Adams-Moulton methods. Math. Comput. Simulation 79 (2008), 1358–1367; 10.1016/j.matcom.2008.03.008.

    Article  MathSciNet  Google Scholar 

  9. B.Y. Guo, T. J. Wang, Composite Laguerre-Legendre spectral method for fourth-order exterior problems. J. Sci. Comput. 44 (2010), 255–285; 10.1007/s10915-010-9367-0.

    Article  MathSciNet  Google Scholar 

  10. L. Guo, F. H. Zeng, I. Turner, K. Burrage, G. E. Karniadakis, Efficient multistep methods for tempered fractional calculus: Algorithms and simulations. SIAM J. Sci. Comput. 41, No 4 (2019), A2510–A2535; 10.1137/18M1230153.

    Google Scholar 

  11. P. Guo, C. Zeng, C. Li, Y. Chen, Numerics for the fractional Langevin equation driven by the fractional Brownian motion. Fract. Calc. Appl. Anal. 16, No 1 (2013), 123–141; 10.2478/s13540-013-0009-8; https://www.degruyter.com/view/journals/fca/16/1/fca.16.issue-1.xml.

    Article  MathSciNet  Google Scholar 

  12. M. Ilic, F. Liu, I. Turner, V. Anh, Numerical approximation of a fractional-in-space diffusion equation (I). Fract. Calc. Appl. Anal. 8, No 3 (2005), 323–341; at http://www.math.bas.bg/complan/fcaa.

    MathSciNet  MATH  Google Scholar 

  13. M. Ilic, F. Liu, I. Turner, V. Anh, Numerical approximation of a fractional-in-space diffusion equation (II): With nonhomogeneous boundary conditions. Fract. Calc. Appl. Anal. 9, No 4 (2006), 333–349; at http://www.math.bas.bg/complan/fcaa.

    MathSciNet  MATH  Google Scholar 

  14. H. Jafari, H. Tajadodi, D. Baleanu, A modified variational iteration method for solving fractional Riccati differential equation by Adomian polynomials. Fract. Calc. Appl. Anal. 16, No 1 (2013), 109–122; 10.2478/s13540-013-0008-9; https://www.degruyter.com/view/journals/fca/16/1/fca.16.issue-1.xml.

    Article  MathSciNet  Google Scholar 

  15. R. Lazarov, P. Vabishchevich, A numerical study of the homogeneous elliptic equation with fractional boundary conditions. Fract. Calc. Appl. Anal. 20, No 2 (2017), 337–351; 10.1515/fca-2017-0018; https://www.degruyter.com/view/journals/fca/20/2/fca.20.issue-2.xml.

    Article  MathSciNet  Google Scholar 

  16. C. Li, Q. Yi, A. Chen, Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 316 (2016), 614–631; 10.1016/j.jcp.2016.04.039.

    Article  MathSciNet  Google Scholar 

  17. C. Li, F. Zeng, F. Liu, Spectral approximations to the fractional integral and derivative. Fract. Calc. Appl. Anal. 15, No 3 (2012), 383–406; 10.2478/s13540-012-0028-x; https://www.degruyter.com/view/journals/fca/15/3/fca.15.issue-3.xml.

    Article  MathSciNet  Google Scholar 

  18. C.P. Li, Q. Yi, Finite difference method for two-dimensional nonlinear time-fractional subdiffusion equation. Fract. Calc. Appl. Anal. 21, No 4 (2018), 1046–1072; 10.1515/fca-2018-0057; https://www.degruyter.com/view/journals/fca/21/4/fca.21.issue-4.xml.

    Article  MathSciNet  Google Scholar 

  19. J.R. Li, A fast time step** method for evaluating fractional integrals. SIAM J. Sci. Comput. 31 (2010), 4696–4714; 10.1137/080736533.

    Article  MathSciNet  Google Scholar 

  20. H.L. Liao, T. Tang, T. Zhou, A second-order and nonuniform time-step** maximum-principle preserving scheme for time-fractional Allen-Cahn equations. J. Comput. Phys. 414 (2020), ID 109473; 10.1016/j.jcp.2020.109473.

  21. F. Liu, M. M. Meerschaert, R. McGough, P. Zhuang, Q. Liu, Numerical methods for solving the multi-term time fractional wave equations. Fract. Calc. Appl. Anal. 16, No 1 (2013), 9–25; 10.2478/s13540-013-0002-2; https://www.degruyter.com/view/journals/fca/16/1/fca.16.issue-1.xml.

    Article  MathSciNet  Google Scholar 

  22. Q. Liu, F. Liu, I. Turner, V. Anh, Y. T. Gu, A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl. Math. Comput. 226 (2014), 336–347; 10.1016/j.amc.2013.10.008.

    MathSciNet  MATH  Google Scholar 

  23. Y. Liu, Y. W. Du, H. Li, J. F. Wang, A two-grid finite element approximation for a nonlinear time-fractional Cable equation. Nonlinear Dyn. 85 (2016), 2535–2548; 10.1007/s11071-016-2843-9.

    Article  MathSciNet  Google Scholar 

  24. M. López-Fernández, C. Lubich, A. Schädle, Adaptive, fast, and oblivious convolution in evolution equations with memory. SIAM J. Sci. Comput. 30 (2008), 1015–1037; 10.1137/060674168.

    Article  MathSciNet  Google Scholar 

  25. C. Lubich, Discretized fractional calculus. SIAM J. Math. Anal. 17 (1986), 704–719; 10.1137/0517050.

    Article  MathSciNet  Google Scholar 

  26. Y. Luchko, Initial-boundary-value problems for the generalized multi-term time fractional diffusion equation. J. Math. Anal. Appl. 374 (2011), 538–548; 10.1016/j.jmaa.2010.08.048.

    Article  MathSciNet  Google Scholar 

  27. H.P. Ma, Y. B. Yang, Jacobi spectral collocation method for the time variable-order fractional mobile-immobile advection-dispersion solute transport model. East Asian J. Appl. Math. 6 (2016), 337–352; 10.4208/eajam.141115.060616a.

    Article  MathSciNet  Google Scholar 

  28. W. McLean, K. Mustapha, A second-order accurate numerical method for a fractional wave equation. Numer. Math. 105 (2007), 481–510; 10.1007/s00211-006-0045-y.

    Article  MathSciNet  Google Scholar 

  29. W. McLean, Exponential Sum Approximations for t−β. In: J. Dick, F. Kuo, H. Woźniakowski (Eds). Contemporary Computational Mathematics-A Celebration of the 80th Birthday of Ian Sloan. Springer, Cham (2018).

    Google Scholar 

  30. T.B. Nguyen, B. Jang, A high-order predictor-corrector method for solving nonlinear differential equations of fractional order. Fract. Calc. Appl. Anal. 20, No 2 (2017), 447–476; 10.1515/fca-2017-0023; https://www.degruyter.com/view/journals/fca/20/2/fca.20.issue-2.xml.

    Article  MathSciNet  Google Scholar 

  31. I. Podlubny, Fractional Differential Equations. Academic Press, San Diego (1999).

    MATH  Google Scholar 

  32. A. Schädle, M. López-Fernández, C. Lubich, Fast and oblivious convolution quadrature; SIAM J. Sci. Comput. 28 (2006), 421–438; 10.1137/050623139.

    Article  MathSciNet  Google Scholar 

  33. R. Schumer, D. A. Benson, M. M. Meerschaert, B. Baeumer, Fractal mobile/immobile solute transport. Water Resour. Res. 39, (2003), 1296-1307; 10.1029/2003WR002141.

  34. J. Shen, T. Tang, L. L. Wang, Spectral Methods: Algorithms, Analysis and Applications. Springer Ser. Comput. Math. Springer, Heidelberg (2011).

    Book  Google Scholar 

  35. M. Stynes, E. O’Riordan, J. Gracia, Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55 (2017), 1057–1079; 10.1137/16m1082329.

    Article  MathSciNet  Google Scholar 

  36. L.L. Wang, Analysis of spectral approximations using prolate spheroidal wave functions. Math. Comput. 79 (2010), 807–827; 10.1090/S0025-5718-09-02268-6.

    Article  MathSciNet  Google Scholar 

  37. F. Zeng, F. Liu, C. Li, K. Burrage, I. Turner, V. Anh, Crank-Nicolson ADI spectral method for the two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 52 (2014), 2599–2622; 10.1137/130934192.

    Article  MathSciNet  Google Scholar 

  38. F. Zeng, Z. Zhang, G. E. Karniadakis, Second-order numerical methods for multi-term fractional differential equations: Smooth and non-smooth solutions. Comput. Methods Appl. Mech. Engrg. 327 (2017), 478–502; 10.1016/j.cma.2017.08.029.

    Article  MathSciNet  Google Scholar 

  39. F. Zeng, I. Turner, K. Burrage, A stable fast time-step** method for fractional integral and derivative operators. J. Sci. Comput. 77 (2018), 283–307; 10.1007/s10915-018-0707-9.

    Article  MathSciNet  Google Scholar 

  40. H. Zhang, F. Liu, M. S. Phanikumar, M. M. Meerschaert, A novel numerical method for the time variable fractional order mobile-immobile advection-dispersion model. Comput. Math. Appl. 66 (2013), 693–701; 10.1016/j.camwa.2013.01.031.

    Article  MathSciNet  Google Scholar 

  41. J. Zhang, C. J. Xu, Finite difference/spectral approximations to a water wave model with a nonlocal viscous term. Appl. Math. Model. 38 (2014), 4912–4925; 10.1016/j.apm.2014.03.051.

    Article  MathSciNet  Google Scholar 

  42. Y. Zhang, D. A. Benson, D. M. Reeves, Time and space nonlocalities underlying fractional-derivative models: Distinction and literature review of field applications. Adv. Water. Resources 32 (2009), 561–581; 10.1016/j.advwatres.2009.01.008.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University **an, 250100, **an, PR China

    Hui Zhang

  2. School of Mathematics, Shandong University, **an, 250100, PR China

    **aoyun Jiang

  3. School of Mathematical Sciences, Queensland University of Technology (QUT), Brisbane, QLD 4001, Australia

    Fawang Liu

Authors
  1. Hui Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. **aoyun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fawang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to **aoyun Jiang.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, H., Jiang, X. & Liu, F. Error Analysis of Nonlinear Time Fractional Mobile/Immobile Advection-Diffusion Equation with Weakly Singular Solutions. Fract Calc Appl Anal 24, 202–224 (2021). https://doi.org/10.1515/fca-2021-0009

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1515/fca-2021-0009

Keywords

Keywords

Search

Navigation