1 Introduction

To ensure the operational and structural safety of bridge structures, structural health monitoring (SHM) systems are often deployed to monitor environmental factors, external loads, structural response and structural variations (Ko and Ni 2005; Ou and Li 2010; Xu and **a 2011; Fu**o and Siringoringo 2008; Xu et al. 2019). Based on available SHM data, extensive data-driven methods were proposed to evaluate bridge condition, detect structural damages/anomalies, and estimate extreme loads (Sun et al. 2020; An et al. 2019; Hou and **a 2021; Avci et al. 2021; Ren et al. 2022). However, SHM data-driven methods suffer from signal noise that plays a significant impact on effectiveness of data-driven algorithms. In this regard, research regarding de-noising for SHM data is highly desired.

Over the last decades, various basic de-noising methods have been introduced to structure engineering to deal with measurements from SHM systems, including low-pass filter (Roberts and Roberts 1978), median filter (George et al. 2018; Yang et al. 1995; Pitas and Venetsanopoulos 2013), adaptive filter (McGillem et al. 1981; Huang et al. 2015), wavelet transform (Staszewski et al. 2000), and empirical mode decomposition (EMD) (Boudraa et al. 2004), etc. Different de-noising algorithms have their own conditions of applicability. Low-pass filters are particularly suitable for high-frequency noise attenuated with the side effect of distorting the original signal (Gupta and Gupta 2013; Dolabdjian et al. 2002). Since the low-pass filter, a linear filtering method, does not handle nonlinear noise or complex noise types well, median filters are introduced to handle scenarios where the data is contaminated with impulse noise (salt-and-pepper noise) or random spikes (George et al. 2018; Tsurkan et al. 2022). In contrast to linear filters, the median filter is less capable of smoothing the data. Moreover, the performance of the median filter can be sensitive to the size of the filtering window (Hamza et al. 1999). Adaptive filters are able to adjust its filter coefficients or parameters in a real-time manner based on the characteristics of the input data, which makes it effectively track and reduce noise even in non-stationary or time-varying noise environments (Dixit and Nagaria 2017). Nonetheless, adaptive filters might overfit to the noise or variations within the data, leading to potential signal distortion or loss of important signal features (Lee and Lee 2005). The wavelet transform has a great effect on processing non-stationary signals and preserving the peak and break section of the useful signal, while the effectiveness of de-noising depends on the choice of initial wavelet function (Garvanov et al. 2019; Zhao 2017; Yan 2019; Wang et al. 2007; Hongmei and Feng 2010). EMD is commonly used for processing signals with time-varying characteristics (Messina et al. 2009). Since the essence of EMD is to decompose the signal into Intrinsic Mode Functions (IMFs) (Huang et al. 2009), it may suffer from mode mixing, where certain IMFs contain mixed information from multiple underlying modes (Han et al. 2017), leading to reduced de-noising performance.

Based on the above de-noising algorithms, scholars have improved them by combination with practical application scenarios. A wavelet-based multilevel filtering approach was implemented in the field of nondestructive testing by taking advantages of the median filtering (Zhang and Wei 2019). Ensemble empirical mode decomposition (EEMD) was applied in reducing the noise of bridge GNSS data, which has good adaptive ability. However, some effective signals will be rejected in the process of noise reduction (Cao et al. 2021). Complete ensemble empirical mode decomposition with adaptive noise-wavelet transformation (CEEMDAN-WT) method can not only effectively solve the problem of modal aliasing, but also extract bridge real displacement information (**ong et al. 2021). EMD and mirror image closed extension method were combined to solve the endpoint effect when obtaining the real deformation of the track structure caused by under-crossing railway project (Pan and Liu 2022). In addition, deep learning algorithms (e.g., deep bidirectional gated recurrent unit recurrent neural network model) have also been applied in the field of signal noise reduction (Li et al. 2022). However, majority of the data-targeted noise reduction methods are on the foundation of a single sensor or signal source, which do not fully utilize the spatial information of multiple sensors, i.e., signal noise reduction is carried out on a two-dimensional level.

In distance speech recognition, beamforming is a classical algorithm to process speech signals from multi-microphones, enhancing the speech of interest with attenuating noise signals by utilizing spatial information (Cho et al. 2019; Liu et al. 2019a). The basic concept of beamforming is to use measured background spatial correlation characteristics to suppress noise and interference, thereby enhancing the beam output and signal-to-noise ratio (SNR) (Cox et al. 1987). In civil SHM systems, information obtained from sensor networks is always of redundancy. Specifically, neighbor sensors capture similar structural response owing to their adjacent locations, which in fact are spatially correlated. Aiming to obtain cleaner data for SHM data-driven analysis, beamforming algorithms are introduced to suppress noise in SHM systems.

This paper develops a beamforming algorithm to obtain robust signals for further data-driven analysis. The monitoring signals are first pre-processed by using missing data imputation and thermal response separation. Then, short-term Fourier transform (STFT) is used to transform time sequences in time domain into time–frequency domain. Subsequently, signals of neighboring sensors are used to compound robust inputs for neural networks using beamforming algorithms. The effectiveness of the beamforming algorithm is illustrated by using measurements of strain gauges installed on steel deck plates.

1.1 Signal processing for SHM

The procedure of signal processing, from measured raw signals to robust signals as inputs of data-driven analysis, is shown in Fig. 1. Data pre-processing is a common step to prepare data for further investigations in the civil SHM research filed. Herein, the data pre-processing includes missing data imputation and thermal response separation. In view of the robustness of algorithms, the measured time sequences are transformed into time–frequency domain using STFT. Beamforming algorithms are employed to obtain robust signals based on measurements from multiple neighboring sensors.

Fig. 1
figure 1

Flowchart of signal processing in SHM systems

Full size image

1.2 Data pre-processing

Data missing is a common phenomenon in SHM systems owing to power depletion, hardware failure, harsh environment attack, etc. Missing data may result in information loss in time and frequency domains of the measured time sequences; in addition, missing data may cause a breakdown of certain data processing algorithms. Methods of missing data imputation are widely studied in the field of SHM. In the presence of a large block of missing data, measurements from other sensors are employed for reconstruction based on the spatial correlations among sensors in the network. The typical approaches include Bayesian learning methodology (Wan and Ni 2019), kernel regression model (Chen et al. 2019), artificial neural networks (Martinez-Luengo et al. 2019), etc.

The temperature action is one of the dominant loadings in civil structures. However, thermal effects are not the response of interest for structural condition assessment or anomaly detection. What is worse, it is quite possible that the wiggling in response of interest is covered by that induced by temperature actions. A significant number of investigations have been carried out in terms of thermal response separation methods, including regression methods (Kromanis and Kripakaran 2014), FE model-based methods (George et al. 2018; Tsurkan et al. 2022), and data-driven methods (Hamza et al. 1999; Dixit and Nagaria 2017; Lee and Lee 2005).

1.3 STFT

The STFT is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local parts of signal as it changes over time. The STFT is devised for analyzing a signal in both time and frequency domain, which is broadly adopted in speech recognition (Hinton et al. 2012; Abdel-Hamid et al. 2014). In the STFT, the Fourier transform of the resulting signal is taken as the window sliding along the time line, resulting in a two-dimensional representation of the signal (Allen 1977). Specifically, to understand the frequency content of the signal at a certain time (t), one should focus on a small portion of the signal at that time and ignore the remaining signal, performing Fourier transform and obtaining a spectrum at that epoch. Subsequently, one takes another small piece of equal length signal at the next instant and get another spectrum. Repeat the above process until the entire signal is sampled. The collection of all these spectrums provide a time–frequency spectrogram that covers the entire signal and captures the localized time-varying frequency content of the signal. Mathematically, we have

$$X\left( {f,t} \right) = \int_{ - \infty }^\infty {w\left( {t - \tau } \right)} x\left( \tau \right){e^{j2\pi f\tau }}d\tau$$
(1)

Where \(X\left( {f,t} \right)\) is the short term frequency spectrum, t is the time variable, \(w\left( {t - \tau } \right)\) is the shifted window, \(x\left( \tau \right)\) is the input signal, and \({e^{j2\pi f\tau }}\) is the complex exponential.

The energy density of the signal and the spectrogram is given by Nagarajaiah (2009)

$$E\left( {f,t} \right) = {\left| {X\left( {f,t} \right)} \right|^2} = {\left| {\int_{ - \infty }^\infty {w\left( {t - \tau } \right)} x\left( \tau \right){e^{j2\pi f\tau }}d\tau } \right|^2}$$
(2)

1.4 Beamforming algorithms

1.4.1 Descriptions of beamforming issue in civil SHM

Beamforming, also known as spatial filtering, is a signal processing technique used in sensor arrays for directional signal transmission or reception, which is one of the most effective approaches for robust recognition of distant speech using multi-microphones. In remote speech recognition, microphone signals obtained from different locations make the beamformer augment the target speech with attenuating noise signals. In beamforming techniques, the minimum-variance distortionless response (MVDR) beamformer is popular since its efficiency in enhancing the target speech by minimizing the power of the beamformed noise signal. Whereas, to obtain an output signal with a high SNR using the MVDR beamformer, it is necessary to accurately estimate the spatial statistics of the noise, i.e., noise covariance matrix (Cho et al. 2019).

Considering the harsh operational environments and degradations of sensors, beamforming algorithms are introduced to civil SHM systems to obtain robust signals for further data analytics. The application of the beamforming algorithm in civil SHM systems must comply with specific requirements. It is essential that the multi-sensors involved are adjacent and of the same type. As discussed earlier, the signals in the time–frequency domain processed by using STFT can be formed as

$${{\mathbf{x}}_{k,l}} = {{\mathbf{S}}_{k,l}} + {{\mathbf{n}}_{k,l}}$$
(3)

Where \({{\mathbf{x}}_{k,l}}\) denotes the vector \(\left( {{x^0}_{k,l},{x^1}_{k,l}, \ldots ,{x^{M - 1}}_{k,l}} \right)\), where the m-th element is the m-th sensor observation at the k-th frequency bin and l-th frame. Similarly, \({{\mathbf{S}}_{k,l}}\) denotes the signal vector of interest, and \({{\mathbf{n}}_{k,l}}\) is the zero-mean noise component.

Generally, a linear filter \({{{\varvec{\upomega}}}_k}\) is applied to the measurements from the sensor array to obtain an enhanced signal, namely

$${Y_{k,l}} = {{\varvec{\upomega}}}_k^H{{\mathbf{x}}_{k,l}}$$
(4)

where H denotes the Hermitian operation on the vector. The applications of a linear filter in the beamforming are shown in Fig. 2.

Fig. 2
figure 2

Linear filter-based beamforming algorithms

Full size image

Based on the idea of beamforming, a general beamforming architecture is devised as shown in Fig. 3 for measurements of civil structures, where M denotes the number of sensors, K is the number of frequency bins, xmk is a vector subject to the k-th frequency bin of the m-th sensor, i.e., xmk = (xmk,0, xmk,1, …, xmk,L-1), and L is the number of frames.

Fig. 3
figure 3

Architecture of beamforming algorithms

Full size image

The minimum-variance response beamformer suppresses noise signals by minimizing the power of a noise component at the beamformer output, which is the optimized objective. In fact, the minimum-variance response beamformer could be formulated into a constrained optimization problem, i.e.,

$$\begin{array}{c}\omega_k=\arg{min}_{\omega k}\omega_k^HR_k^n\omega_k,\\ s.t.\sum_{m=0}^{M-1}\omega_k^m=1\\ \omega_k^m-1\leq0,\left(0\leq m\leq M-1\right)\end{array}$$
(5)

where \({\mathbf{R}}_k^n\) is the noise covariance matrix, which is expressed as

$${\mathbf{R}}_k^n = E\left[ {{{\mathbf{n}}_k}{\mathbf{n}}_k^H} \right]$$
(6)

Equation (5) and (6) illustrate the optimized rules for the beamforming process.

1.4.2 Constrained optimization using interior point algorithm

As shown in Eq. (5), the beamforming issue in civil SHM is formulated into a constrained optimization problem. The interior point method is a type of algorithm used in solving both linear and nonlinear convex optimization problems (Wächter and Biegler 2006; Liu et al. 2019b).

1.4.3 The general constrained optimization problem is expressed as

$$\begin{array}{c}\min_xf\left(x\right),\\ s.t.h\left(x\right)=0\\ \mathrm g\left(x\right)\leq 0 \end{array}$$
(7)

In this article, \(f\left( x \right)\) denotes \({{\varvec{\upomega}}}_k^H{\mathbf{R}}_k^n{{{\varvec{\upomega}}}_k}\), \(h\left( x \right)\) equals to \(\sum\limits_{m = 0}^{M - 1} {\left| {{\omega^m}_k} \right|} - 1\), and \(g\left( x \right)\) is \(\left| {{\omega^m}_k} \right| - 1\). In order to get rid of the inequality constraints, for each barrier parameter \(\mu > 0\), the approximate problem is given as

$$\mathop {\min }\limits_{x,s} {f_\mu }\left( {x,s} \right) = \mathop {\min }\limits_{x,s} \left[ {f\left( x \right) - \mu \sum\limits_i {\ln \left( {s_i} \right)} } \right], s.t.h\left(x\right)=0$$
(8)

Where si is the slack variables associated with the number of inequality constraints g(x). si is restricted to be positive to keep ln(si) bounded. As \(\mu\) decreases to zero, the minimum of \({f_\mu }\) should approach the minimum of f. The added logarithmic term is called a barrier function.

The approximate problem, Eq. (8), is a sequence of equality constrained problems, which are easier to solve than the original inequality-constrained problem. Subsequently, the equality constraints are incorporated into the objective function using Lagrange multipliers, namely

$$L\left( {x,s,{\lambda_h},{\lambda_g}} \right) = f\left( x \right) - \mu \sum\limits_i {\ln \left( {s_i} \right)} + \lambda_h^Th\left( x \right) + \lambda_g^T\left( {g\left( x \right) + s} \right)$$
(9)

where \({\lambda_h}\) and \({\lambda_g}\) are the Lagrange multipliers. An approximate solution \(\left( {\hat x,\hat s} \right)\) is implemented instead of the accurate solution of Eq. (8), where \(\left( {\hat x,\hat s} \right)\) satisfies the condition

$$E\left( {x,s;\mu } \right) = \max \left( {{{\left\| {\nabla f\left( x \right) + \nabla h{{\left( x \right)}^T}{\lambda_h} + \nabla g{{\left( x \right)}^T}{\lambda_g}} \right\|}_\infty },{{\left\| {S{\lambda_g} - \mu e} \right\|}_\infty },{{\left\| {h\left( x \right)} \right\|}_\infty },{{\left\| {g\left( x \right) + s} \right\|}_\infty }} \right) \leqslant {\varepsilon_\mu }$$
(10)

here e is the vector of all ones with appreciate dimension, S = diag(s0, s1,…, sM-1), \(\nabla h\left( x \right)\) and \(\nabla g\left( x \right)\) are the Jacobian of the constraint vectors h(x) and g(x), and \({\varepsilon_\mu }\) is the tolerance, which determines the accuracy in the solution of the barrier problems.

After computing Lagrange multiplier estimates \(\left( {{\lambda_h},{\lambda_g}} \right)\), we formulate the subproblem.

$$\begin{array}{c}\min_{\Delta x,\Delta s}\left\{\nabla f\left(x\right)^T\Delta x+\frac12\Delta x^T\nabla_{xx}^2L\left(x_k,s_k,\lambda_h,\lambda_{\mathrm g}\right)\Delta x-{\mu e}^TS_k^{-1}\Delta s+\frac12{\Delta s}^T\sum\nolimits_k\Delta s\right\}\\ s.t.\;\begin{array}{c}\nabla h\left(x_k\right)^T{\Delta x}_k+h\left(x_k\right)=r_h,\\ \nabla h\left(x_k\right)^T{\Delta x}_k+{\Delta s}_k+\mathrm g\left(x_k\right)+s_k=r_{\mathrm g}\end{array}\end{array}$$
(11)

In which \(\sum {_k}\) is the Hessian of the Lagrange Eq. (9) with respect to s. Ideally, we would like our step to make \(r = \left( {{r_h},{r_g}} \right) = 0\).

Equivalently, Eq. (9) can be interpreted as applying a homotopy method for the primal–dual system, we obtain

$$\begin{aligned} \nabla f\left( x \right) + \nabla h{\left( x \right)^T}{\lambda_h} + \nabla g{\left( x \right)^T}{\lambda_g} = 0, \hfill \\ - \mu {S^{ - 1}}e + {\lambda_g} = 0, \hfill \\ h\left( x \right) = 0, \hfill \\ g\left( x \right) + s = 0. \hfill \\ \end{aligned}$$
(12)

Given a primal–dual iterate \(\left( {{x^{\left( k \right)}},{s^{\left( k \right)}},{\lambda_h}^{\left( k \right)},{\lambda_g}^{\left( k \right)}} \right)\) that fulfills the positivity constraints, the Karush–Kuhn–Tucker system is solved as

$$\left[ {\begin{array}{*{20}{c}} {\nabla_{xx}^2{L_k}}&0&{\nabla h\left( x \right)}&{\nabla g{{\left( x \right)}^T}} \\ 0&{\nabla_{ss}^2{L_k}}&0&I \\ {\nabla h{{\left( x \right)}^T}}&0&0&0 \\ {\nabla g{{\left( x \right)}^T}}&I&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\vartriangle x} \\ {\vartriangle s} \\ {\lambda_h^+ } \\ {\lambda_g^+ } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \nabla f\left( {x_k} \right)} \\ {\mu S_k^{ - 1}e} \\ { - h\left( {x_k} \right)} \\ { - g\left( {x_k} \right) - {s_k}} \end{array}} \right]$$
(13)

where \(\nabla_{xx}^2{L_k}\) denotes the Hessian of the Eq. (9) with respect to x, which is expresses as \(\nabla_{xx}^2{L_k} = {\nabla^2}f\left( x \right) + {\nabla^2}h{\left( x \right)^T}{\lambda_h} + {\nabla^2}g{\left( x \right)^T}{\lambda_g}\), and \(\nabla_{ss}^2{L_k}\) is the Hessian of the Eq. (9) with respect to s.

Choose an initial value for the barrier parameter \(\mu > 0\), and select the parameters \({\varepsilon_\mu } > 0\), \(\theta \in \left( {0,1} \right)\), and the final stop tolerance \({\varepsilon_{TOL}}\). Choose the starting point x and s, and evaluate the objective function, constraints, and their derivatives at x.

Repeat until \(E\left( {x,s;\mu } \right) \leqslant {\varepsilon_{TOL}}\):

  1. 1.

    Start from (x, s) to find an approximate solution (x+, s+) of the barrier problem Eq. (8) satisfying \(E\left( {{x_k},{s_k};\mu } \right) \leqslant {\varepsilon_\mu }\), i.e.,

Repeat until \(E\left( {{x_k},{s_k};\mu } \right) \leqslant {\varepsilon_\mu }\):

Compute \(\vartriangle = \left( {\vartriangle x,\vartriangle s} \right)\) by approximately solving Eq. (11).

If the step \(\vartriangle\) provides sufficient decrease.

then set \({x_{k + 1}} = {x_k} + \vartriangle x,{s_{k + 1}} = {s_k} + \vartriangle s\),

compute new Lagrange multiplier estimates \({\lambda_h}\) and \({\lambda_g}\),

and possibly enlarge the trust region;

else set \({x_{k + 1}} = {x_k},{s_{k + 1}} = {s_k}\), and shrink the trust region.

Set k=k+1.

  1. 2.

    Set \(\mu \leftarrow \theta \mu ,{\varepsilon_\mu } \leftarrow \theta {\varepsilon_\mu },x \leftarrow {x^+ },s \leftarrow {s^+ }.\)

2 Case study

2.1 The 3rd Nan**g Yangtze river bridge and its monitoring system

The 3rd Nan**g Yangtze River Bridge is a vital transportation link crossing the middle and lower Yangtze River and connecting Nan**g City and its Liuhe District. It is a two-tower cable-stayed bridge with a main span of 648 m as shown in Fig. 4. The superstructure deck has a depth of 3.2 m and the orthotropic steel box girder has a width of 37.5 m to accommodate three traffic lanes in each direction. The deck is supported by a total of 168 stay cables and each cable consists of 109 to 241 wires having a diameter of 7 mm.

Fig. 4
figure 4

Layout of the 3rd Nan**g Yangtze River Bridge

Full size image

Measurements of the strain gauges (D1, D2 and D3) at the mid-span section are used to validate the effectiveness of the proposed beamforming algorithm. The deployment of the sensor gauges is shown in Fig. 5, where the sampling frequency of the strain gauge is 10 Hz. The measurements of the selected three sensors all reflect the characteristics of vehicle loadings on the half of the driveway (downstream) and the response of the steel deck.

Fig. 5
figure 5

Deployment of the stain gauges at the mid-span section

Full size image

2.2 Data pre-processing

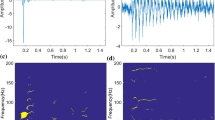
Data obtained from the three strain gauges (D1, D2 and D3) in one hour (9:00 a.m. ~ 10:00 a.m., Mar. 1, 2007) are used to illustrate the proposed approach. The missing data solution is to propagate the last valid observation forward to the next one. The measurements of the three sensors are shown in Fig. 6 after completion of missing data imputation. Significant trends are observed as the red arrows in Fig. 6, which are induced by thermal actions.

Fig. 6
figure 6

Measurements obtained from the three strain gauges

Full size image

Wavelet-based multi-resolution analysis is used to separate thermal response. Based on trials and errors, the stress signals are decomposed into 8 layers with the wavelet basis function ‘db12’. The low frequency components corresponding to the temperature-induced variations are separated from the original signals. The qualified signals after thermal response separation are shown in Fig. 7. The variation trends of the measurements from the three sensors are highly correlated as shown in Fig. 7(d), which shows that the effect of thermal response separation is significant.

Fig. 7
figure 7

Signals after thermal response separation

Full size image

2.3 STFT

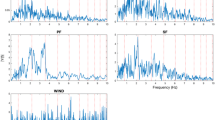
STFT is applied to the qualified signals shown in Fig. 7 to obtain information in both time and frequency domain. With the Hamming window of length 128, 50% overlap between segments, the FFT length of 128, and the sampling frequency of 10 Hz, the spectrograms of the qualified signals from the three strain gauges are shown in Fig. 8. As a result, most of the signal energy focuses on the frequency bandwidth between 0 Hz and 0.40 Hz.

Fig. 8
figure 8

STFT spectrum of the three strain gauges

Full size image

2.4 Beamforming process

According to the beamforming algorithms, noise signals are necessary to determine the linear filter corresponding to sensors. Herein, measurements obtained from the sensor during bridge closure time windows are treated as noise signals. The measurements of the three sensors (D1, D2 and D3) between 07:00 a.m. and 08:00 a.m. on Mar. 25, 2007 (bridge closure time window) are shown in Fig. 9, which are pre-processed by missing data imputation.

Fig. 9
figure 9

Noise signals obtained from the three sensors

Full size image

Wavelet-based multi-resolution method is used to separate thermal response from the noise signal, and STFT is then used to obtain the spectrum as shown in Fig. 10. The noise signals are of stationary type, which means that the statistics of the noise (e.g., spectrum shape) remain constant with respect to the time line. The energy of the noise signals mainly lies in two frequency bandwidths, i.e., [0.2 Hz, 1.3 Hz] and [1.9 Hz, 2.7 Hz].

Fig. 10
figure 10

STFT spectrum of the noise signal from the three sensors

Full size image

Since the beamforming process not only suppresses noise but also the signals of interest, signals subject to noise frequency bandwidths are processed by using the beamforming algorithm. Considering the overlap of frequency bandwidths between the obtained measurements and noise, frequency bandwidths of [0.4 Hz,1.3 Hz] and [1.9 Hz, 2.7 Hz] are used for beamforming discussions.

Interior point algorithm is adopted to determine the linear filter to minimize the variance response as shown in Eq. (5). Noise signals corresponding to frequency bin of 0.391 Hz are taken as an example to demonstrate the optimization process. The variables involved in the optimization procedure include real parts of the three weights (i.e., X(1), X(2) and X(3)) and image parts of the three weights (i.e., X(4), X(5) and X(6)). The optimization process is shown in Fig. 11, where the current point is the present optimum solutions, function count reports the number of times that the objective function was evaluated, function value indicates the value of the objective function, constraint violation is the maximum constraint violation value of each iteration, step size is the algorithm step size at each iteration, and first-order optimality is the violation of the optimality conditions for the solver at each iteration. According to the optimization results, the constraint conditions are strictly obeyed, and the optimum linear filters of the three sensors are (0.1361 + 0.2856i), (0.3160–0.0726i) and (-0.0193 + 0.3589i), respectively. Similarly, linear filters of the other frequency bins could be obtained through the same optimization process.

Fig. 11
figure 11

Parameters in the optimization process

Full size image

3 Results and discussions

Following the above optimization process, the optimum linear filters subject to the three sensors are listed in Table 1.

Table 1 Optimum linear filter corresponding to the three sensors
Full size table

Applying the optimum linear filter to the noise signal, the noise is substantially suppressed, especially in the frequency bandwidth [1.9 Hz,2.7 Hz] as shown in Fig. 12(a). Aiming to validate the effectiveness of the proposed spatial filtering method, the linear filter is used to reduce the noise in the studied signals as shown in Fig. 8. As a result, the power spectral density corresponding to the noise frequency bandwidths is significantly reduced compared with the signals obtained from the single sensor. The specific beamformer output is shown in Fig. 12(b). SNR is introduced to quantitatively rate the efficiency of the proposed spatial filtering. The SNRs of the measurements obtained from the three strain gauges are 33.5 dB, 32.6 dB and 31.9 dB, respectively. After the beamforming process, the SNR increases to 35.3 dB. The SNR is not significantly improved since the spatial filtering not only suppress the noise but also the signal of interest.

Fig. 12
figure 12

Spatial filtering results of the noise and studied signal

Full size image

4 Conclusions and prospects

This paper explores to introduce the beamforming algorithm into data processing in civil SHM fields to achieve robust signals for further investigations. The following conclusions can be drawn from this study:

  1. (1)

    In view of the deployment of sensors in civil structures, information redundancy of measurements from various sensors is common in civil SHM fields. The spatial correlations between signals from different sensors provide foundations for spatial filtering.

  2. (2)

    Following the concept of the beamforming algorithm in distance speech recognition, the beamforming algorithm in civil SHM fields is summarized into a constrained optimization problem. The interior point algorithm is adopted to address the optimization problem.

Measurements of strain gauges from the 3rd Nan**g Yangtze River Bridge during normal service time windows and closure time windows are used to verify the effectiveness of the proposed beamforming algorithm. As a result, the SNRs of the measurements obtained from the three strain gauges are 33.5 dB, 32.6 dB and 31.9 dB, respectively. After the beamforming process, the SNR increases to 35.3 dB, which has an average increase of 8.3%. Obviously, with the applications of the linear filter, the noise in the beamformer outputs is significantly suppressed when compared with the signal from the single sensor. In conclusion, the robustness of signals is improved by use of the beamforming algorithm, which provides high quality data source for further studies.

The present study mainly focuses on the de-noising aspect by use of spatial filtering. However, sensor faults are common in practical engineering owing to the manufacturing flaws, harsh operation environment and performance degradation. Future study can be conducted regarding obtaining robust signals with the interference of sensor faults.