Introduction

Since wind energy is green and renewable, as advertised by global political agenda nowadays, energy harvesters (EH) became recently a popular research topic. Engineering research is also being done on micro- and nano-size EHs. Micro-scale wind energy is captured using piezoelectric, triboelectric, and electrostatic EHs; macro-scale wind energy is captured using an electromagnetic EH. Low-frequency EHs technology has been recently shown to be practical and advantageous. These innovations have been developed to supply energy to a variety of low-cost, low-power gadgets, including MEMS and Wireless Sensor Networks (WNS). It has been demonstrated that piezoelectric vibration energy harvesting (PVEH) is able to transform environmental mechanical vibrational energy into electrical energy. Mechanical vibration is of an irregular and intermittent nature, resulting in aero-instability in the form of resonant vibrations. Thus, employing flow-induced vibrations (FIVs) to generate energy has been proven to be practical. Vortex-Induced Vibrations (VIV), wake gallo**, gallo**, and other related phenomena represent examples of FIVs. In the past decade, various investigations have utilized innovative experimental, numerical, and theoretical methods. In Albaladejo et al. (2010) the authors introduced a model for EH aero-instability coupling. In Mehmood et al. (2013) the authors presented the CFD approach to describe VIV Piezoelectric Energy Harvesters (VIVPEH). In Fazeres-Ferradosa et al. (2018a) the authors studied the Galerkin algorithm, applied to theoretical VIV piezoelectric EH features, with a series of laboratory tests carried out to examine the optimization process of a multifunctional VIVPEH device. In recent research (Dai et al., 2014) the authors have reported a transition from VIVPEH to GPEH, by adding 2 Y-shaped attachments. In Wang et al. (2019) the authors have used bistable and tristable features, subsequently examining GPEH nonlinear system response.

Energy harvesting systems are significant in both offshore and onshore applications. The hazards of ocean pollution are progressively rising as the oceanic industry increases. Devices for monitoring the water, such as various types of sensors, are created to address this kind of issue. Data can be gathered from remote locations and sent to local stations using sensors (Albaladejo et al., 2010; Zhao et al., 2019) have investigated the reliability and durability of the P1 MFC transducer, subjected to base excitations. In Wang et al. (2020) the authors reported experimental findings, where EH suffered damage at acceleration levels of 0.4 to 0.5 g. In Zhao and Yang (2018) the authors studied the EH performance of DuraAct (DuraAct P-876.A12 from Physik Instrumente GmbH & Co. KG.) piezo-sheet mounted EH on the railway, EH was reported to fail after about 100 cycles, under acceleration of 1 g. Next, in Daqaq (2015) the authors have applied a P-2 MFC sheet, using finite element method (FEM) and laboratory tests to study long-term fatigue life of EH. In Gaidai et al. (2006a). There have not been much studies done on the reliability of wind-induced vibrational EH dynamic performance, supported by experimental tests. Few studies have examined the EH system extreme performance and, consequently, reliability, and safety of EH operating conditions. Recent studies have typically concentrated on EH’s beam behavior under fatigue loadings, due to specific excitations, to estimate EH’s lifetime.

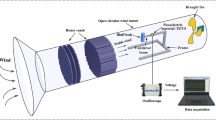
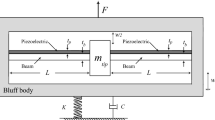
This study focuses on extreme value statistics of the GPEH dynamic system’s response. Both theoretical and experimental research have been done in order to examine the dynamic performance of particular gallo** EH. The experimental setup and specifics of the EH bluff body have been presented in Fig. 1. GPEH dynamic performance has been evaluated in a wind tunnel, using a circular inlet cross section. By installing a honeycomb structure within a wind tunnel’s settling chamber, having a diameter of 400 mm, steady incoming air flow was created, and wind speed ranged within 1 ≤ U ≤ 6 m/s. Piezoelectric sheet (Model: PZT-5, JiaYeShi, China) of 30 × 20 × 0.5 mm3 has been mounted on a substrate, made of aluminum, having dimensions of 200 × 25 × 0.5 mm3 when designing the GPEH cantilever. Free-end of the GPEH piezoelectric cantilever has been attached to a circular-sectioned bluff body (Wang et al., 2020). GPEH bluff body has been made of a hardened foam, having a length of 0.12 m, and a diameter of 0.03 m. Prototyped GPEH piezoelectric cantilever dam** ratio ζ has been measured, using the logarithmic decremental technique. For physical parameters of the GPEH experimental prototype, see Table 1, where \({C}_{p}\) is GPEH’s piezoelectric transducer clam** capacitance; \(M\) being GPEH’s bluff body effective mass; \({\zeta }_{1}\) GPEH’s dam** ratio; \({\omega }_{1}\)—GPEH’s natural vibrational frequency; \(\theta \)—equivalent electromechanical coefficient, for further details, see (Wang et al., 2020).

Fig. 1
figure 1

Wind tunnel experimental setup

Full size image
Table 1 GPEH experimental prototype geometrical and physical parameters
Full size table

The free end of EH’s circular-sectioned bluff body has been attached to its piezoelectric cantilever (Albaladejo et al., 2010). Incoming wind speed U has been measured, using hot-wire anemometer (Model: 405i, Testo Co., USA). GPEH voltage output has been measured, using a digital oscilloscope (Model: DS1104S, RIGOL., China), for GPEH experimental setup see (Wang et al., 2019).

It is important to note that a GPEH’s intended use is to practically harvest low-speed wind energy: U ≤ 7 m/s, within the so-called “strong-breeze” region, Table 2.

Table 2 Wind speed ranges (below 7 m/s)
Full size table

Traditional propeller generators work better, when wind speed is high (7 m/s and above) because their motor size better matches these wind speeds.

Finally, it is worth mentioning a variety of other existing GPEH types: enhanced GPEH, having cooperative modes of collisions and vibrations, (Rugbjerg et al., 2006b); EH with self-regulating triboelectric nano-generators, self-powered wind speed sensor (Franck & Luc, 2011; Larsen et al., 2015; Mouslim et al., 2008; Teena et al., 2012); magnetically coupled water-proof piezoelectric-electromagnetic hybrid wind EH (Cheng et al., 2003; Cook & Harris, 2004; Ewans, 2014; Heffernan & Tawn, 2004; Jensen & Capul, 2006; Kim & Lee, 2015; Li et al., 2013; Zhao & Ono, 1999). This study is structured as follows: in the next section novel reliability methodology will be introduced, followed by the application of this reliability methodology to a particular GPEH device and its laboratory-recorded measurements.

Method

This section describes the Naess–Gaidai (NG) extrapolation approach (Gaidai et al. 2023a; Zhang et al. 2018), which is based on Weibull distribution with 3 parameters, and is applicable to a variety of unidimensional random system components. The requirement to do long-term statistical analysis for the structure of interest typically drives motivation for reliability study in engineering and design. The 3-parameter Weibull distribution is briefly introduced in the paragraph that follows. In reliability analysis, Weibull distribution has proved a potent choice: in contrast to exponential distribution, it offers a significantly wider application range. In reliability engineering, Weibull distribution is a viable substitute for both Gamma and Lognormal distributions. Weibull and exponential distributions have recently been given a number of weighted iterations in the literature

$$ G\left( {x,\lambda ,\beta ,\theta } \right) = 1 - e^{{ - \lambda_{W} \left( {x - \theta } \right)^{\beta } }} $$
(1)

with \({\lambda }_{W},\beta ,\theta \) being the scale, shape, and minimum lifespan (location) parameters respectively, and \({\lambda }_{W}>0, \beta >0, x>\theta \). In lifetime data analysis, \(\theta \) is typically referred to as a threshold, guarantee time or a parameter, and \({\lambda }_{W}\) is the mean time to failure. NG method is based on adding 1 more parameter \(q\) to the 3-parameter Weibull’s distribution

$$ G\left( {x,\lambda ,\beta ,\theta } \right) = 1 - qe^{{ - \lambda_{W} \left( {x - \theta } \right)^{\beta } }} $$
(2)

with \(q>0\).Weibull distribution is well suited for modeling different environmental loadings, as well as structural reactions to such loadings. The distribution described by Eq. (2) will be referred to as “modified Weibull” or “4-parameter Weibull” in the sections that follow. As can be demonstrated, the essence of the NG technique—the modified Weibull distribution, happens to be a suitable approximation for empirical probability density function (PDF) tails, namely when \(x\to \infty \), for various engineering and design problems. As is customary in wind engineering, we will demonstrate the advocated approach in the sections that follow, by completing so-called short-term analyses for stationary environmental conditions. In situ scatter diagram, which will not be discussed in this study because it is being common knowledge, may be used for long-term analysis. In general, it is often challenging to assess realistic environmental system reliability function, using established theoretical reliability methodologies (Aarnes et al. 2012; Battjes and Groenendijk 2000; Bidlot and Janssen 2003; Cook and Harris 2004; Ferreira and Guedes 2000; Franck and Luc 2011; Gaidai et al. 2020, 2022; Zhao et al., 2019; Zhou et al., 2019). Utilizing classic theoretical reliability approaches to assess a system’s reliability is not an easy and straightforward task. Typically, it is assumed that wind speeds represent an ergodic random process (quasi-stationary and homogenous) (Cheng et al., 2022; Gaidai & **ng, 2022a, b; Gaidai et al., 2022b, c, d, e, f, g, h; Xu et al., 2022). Think of an MDOF (multi-degree of freedom) EH system, subjected to in situ environmental loads (Balakrishna et al., 2022; Gaidai & **ng, 2022a, c; Gaidai et al., 2022c, d, e, g, h, i, j, k). Another option is to view the EH system process as being dependent on external (environmental) factors, whose temporal fluctuation may be modeled as ergodic processes. MDOF EH dynamic system being represented through its critical/key components \(\left(X\left(t\right), Y\left(t\right), Z\left(t\right),\dots \right)\) that have been measured/simulated over a representative time span \((0,T)\). One-dimensional system components global maxima over entire time lapse \((0,T)\) being denoted here as \({X}_{T}^{\text{max}}=\underset{0\le t\le T}{\text{max}}X\left(t\right)\), \({Y}_{T}^{\text{max}}=\underset{0\le t\le T}{\text{max}}Y\left(t\right)\), \({Z}_{T}^{\text{max}}=\underset{0\le t\le T}{\text{max}}Z\left(t\right), \dots \). By representative time lapse \(T\) one means large enough value of \(T\), with respect to dynamic system’s auto-correlation as well as relaxation time scales. Let \({X}_{1},\dots ,{X}_{{N}_{X}}\) be temporally consequent EH system component’s \(X(t)\) local maxima, recorded at discrete, monotonously increasing time instants \({t}_{1}^{X}<\dots <{t}_{{N}_{X}}^{X}\) within \((0,T)\) Analogous definition to follow for other MDOF EH system’s components \(Y\left(t\right), Z\left(t\right), \dots \) with \({Y}_{1},\dots ,{Y}_{{N}_{Y}};\) \({Z}_{1},\dots ,{Z}_{{N}_{Z}}\) etc. For simplicity, all EH system’s components local and hence global maxima are assumed to be positive. The target is now to accurately estimate the system’s failure/hazard/damage probability, namely probability/risk of exceedance

$$ 1 - P = {\text{Prob}}\left( {X_{T}^{{{\text{max}}}} > \eta_{X} \cup Y_{T}^{{{\text{max}}}} > \eta_{Y} \cup Z_{T}^{{{\text{max}}}} > \eta_{Z} \cup \ldots } \right) $$
(3)

with

$$ P = \int {\int {\int_{{\left( {0, 0, 0, , \ldots } \right)}}^{{\left( {\eta_{X} , \eta_{Y} , \eta_{Z } , \ldots } \right)}} {p_{{X_{T}^{{{\text{max}}}} , Y_{T}^{{{\text{max}}}} , Z_{T}^{{{\text{max}}}} , \ldots }} \left( {x_{T}^{{{\text{max}}}} , y_{T}^{{{\text{max}}}} , z_{T}^{{{\text{max}}}} , \ldots } \right)} } } {\text{d}}x_{T}^{{{\text{max}}}} {\text{d}}y_{T}^{{{\text{max}}}} {\text{d}}z_{T}^{{{\text{max}}}} \ldots $$
(4)

being target non-exceedance (survival) system probability, given critical values of EH system’s components \({\eta }_{X}\), \({\eta }_{Y}\), \({\eta }_{Z}\),…; with \(\cup \) being logical unity operation «or»; and \({p}_{{X}_{T}^{\text{max}}, { Y}_{T}^{\text{max}}, { Z}_{T}^{\text{max}} , \dots }\) being joint PDF of EH system component’s global maxima over entire observational time-span \((0,T)\). In practice, however, it is not feasible to assess directly the latter joint PDF \({p}_{{X}_{T}^{\text{max}}, { Y}_{T}^{\text{max}}, { Z}_{T}^{\text{max}} , \dots }\) due to the system’s high dimensionality, and underlying dataset limitations. More specifically, when either component \(X\left(t\right)\) exceeds \({\eta }_{X}\), or \(Y\left(t\right)\) exceeds \({\eta }_{Y}\), or \(Z\left(t\right)\) exceeds \({\eta }_{Z}\), etc., EH system is regarded as immediately failed. Fixed hazard/failure levels \({\eta }_{X}\), \({\eta }_{Y}\), \({\eta }_{Z}\),… being individual for each one-dimensional system’s component. \({X}_{{N}_{X}}^{\text{max}}=\text{max }\{{X}_{j}\hspace{0.17em};j=1,\dots ,{N}_{X}\}={X}_{T}^{\text{max}}\), \({Y}_{{N}_{Y}}^{\text{max}}=\text{max }\{{Y}_{j}\hspace{0.17em};j=1,\dots ,{N}_{Y}\}={Y}_{T}^{\text{max}}\), \({Z}_{{N}_{z}}^{\text{max}}=\text{max }\{{Z}_{j}\hspace{0.17em};j=1,\dots ,{N}_{Z}\}={Z}_{T}^{\text{max}}\), etc. Now, let us sort EH dynamic system component’s local maxima time instants \(\left[{t}_{1}^{X}<\dots <{t}_{{N}_{X}}^{X}; {t}_{1}^{Y}<\dots <{t}_{{N}_{Y}}^{Y}; {t}_{1}^{Z}<\dots <{t}_{{N}_{Z}}^{Z}\right]\) in a monotonously non-decreasing order into one single merged time vector \({t}_{1}\le \dots \le {t}_{N}\). Note that \({t}_{N}=\text{max }\{{t}_{{N}_{X}}^{X}, {t}_{{N}_{Y}}^{Y}, { t}_{{N}_{Z}}^{Z}, \dots \}\), \(N\le {N}_{X}+{N}_{Y}+{ N}_{Z}+ \dots \). In this case, \({t}_{j}\) represents occurrences times of EH component local maxima of one of MDOF system components, namely either \(X\left(t\right)\) or \(Y\left(t\right)\), or \(Z\left(t\right)\) etc. Next, we screen continuously, concurrently for the EH system component’s local maxima, within EH one-dimensional system components, recording their exceedances of MDOF limit/hazard/risk vector \(\left({\eta }_{X}, {\eta }_{Y}, {\eta }_{Z},...\right)\) by any of EH system’s components \(X, Y, Z, \dots \) Local one-dimensional EH system component maxima have been merged now into 1 temporal non-decreasing system vector \(\overrightarrow{R}=\left({R}_{1}, {R}_{2}, \dots ,{R}_{N}\right)\) in accordance with the merged temporal vector \({t}_{1}\le \dots \le {t}_{N}\). Hence, EH component’s local maxima \({R}_{j}\) is in fact actually encountered the EH system component’s local maxima, corresponding to either \(X\left(t\right)\) or \(Y\left(t\right)\), or \(Z\left(t\right)\) and so on. Finally, a unified limit/hazard system vector \(\left({\eta }_{1}, \dots ,{\eta }_{N}\right)\) is introduced, with each EH system component \({\eta }_{j}\) being either \({\eta }_{X}\), \({\eta }_{Y}\) or \({\eta }_{Z}\) and so on, depending which of \(X\left(t\right)\) or \(Y\left(t\right)\), or \(Z\left(t\right)\) etc. corresponding to the current EH component’s local maxima, having a running index \(j\). Scaling parameter \(0<\lambda \le 1\) is being introduced to simultaneously decrease limit/hazard values for all EH dynamic system components, namely new MDOF hazard/limit vector \(\left({\eta }_{X}^{\lambda },{ \eta }_{Y}^{\lambda }, {\eta }_{z}^{\lambda },...\right)\) with \({\eta }_{X}^{\lambda }\equiv \lambda {\cdot \eta }_{X}\), \(\equiv \lambda {\cdot \eta }_{Y}\), \({\eta }_{z}^{\lambda }\equiv \lambda {\cdot \eta }_{Z}\),… being now introduced. A unified limit vector \(\left({\eta }_{1}^{\lambda }, \dots ,{\eta }_{N}^{\lambda }\right)\) being introduced with each component \({\eta }_{j}^{\lambda }\) being either \({\eta }_{X}^{\lambda }\), \({\eta }_{Y}^{\lambda }\) or \({\eta }_{z}^{\lambda }\) etc. The latter identifies system’s survival probability \(P\left(\lambda \right)\) as a function of parameter \(\lambda \), note that \(P\equiv P\left(1\right)\) from Eq. (1). Non-exceedance (survival) probability/risk \(P\left(\lambda \right)\) may be now assessed

$$ \begin{aligned} P\left( \lambda \right) & = {\text{Prob}}\left\{ {R_{N} \le \eta _{N}^{\lambda } , \ldots ,R_{1} \le \eta _{1}^{\lambda } } \right\} = \\ & = {\text{Prob}}\left\{ {R_{N} \le \eta _{N}^{\lambda } ~{\text{|}}~R_{{N - 1}} \le \eta _{{N - 1}}^{\lambda } , \ldots ,R_{1} \le \eta _{1}^{\lambda } } \right\} \cdot {\text{Prob}}\left\{ {R_{{N - 1}} \le \eta _{{N - 1}}^{\lambda } , \ldots ,R_{1} \le \eta _{1}^{\lambda } } \right\} \\ & = \mathop \prod \limits_{{j = 2}}^{N} {\text{Prob}}\left\{ {R_{j} \le \eta _{j}^{\lambda } ~|~R_{{j - 1}} \le \eta _{{1j - }}^{\lambda } , \ldots ,R_{1} \le \eta _{1}^{\lambda } } \right\} \cdot {\text{Prob}}\left( {R_{1} \le \eta _{1}^{\lambda } } \right) \\ \end{aligned} $$
(5)

The idea behind this series of conditioning-based approximations is explained in detail in Gaspar et al. (2012), Gaidai et al. (2023g), Naess et al. (2009), Xu et al. (2018). Dependence between neighboring \({R}_{j}\) is not always negligible, hence following 1-step (conditioning number \(k=1\) memory approximation being introduced

$$ {\text{Prob}}\{ R_{j} \le \eta_{j}^{\lambda } | R_{j - 1} \le \eta_{j - 1}^{\lambda } , \ldots ,R_{1} \le \eta_{1}^{\lambda } \} \approx {\text{Prob}}\{ R_{j} \le \eta_{j}^{\lambda } | R_{j - 1} \le \eta_{j - 1}^{\lambda } \} $$
(6)

for \(2\le j\le N\) (conditioning number \(k=2\)). Approximation, introduced by Eq. (6) may be now further expressed as

$$ \begin{gathered} {\text{Prob}}\left\{ {R_{j} \le \eta_{j}^{\lambda } {|} R_{j - 1} \le \eta_{j - 1}^{\lambda } , \ldots ,R_{1} \le \eta_{1}^{\lambda } } \right\} \approx \hfill \\ \approx {\text{Prob}}\left\{ {R_{j} \le \eta_{j}^{\lambda } | R_{j - 1} \le \eta_{j - 1}^{\lambda } , R_{j - 2} \le \eta_{j - 2}^{\lambda } } \right\} \hfill \\ \end{gathered} $$
(7)

with \(3\le j\le N\) (conditioning number \(k=3\)), etc. (Balakrishna et al., 2022; Gaidai et al., 2022g, 2022h, 2022i, 2022j, 2022k). The idea is to monitor each independent damage/hazard/failure, that happened locally first in time, thus avoiding (de-clustering) cascading inter-correlated local exceedances. Since the MDOF EH system has been assumed ergodic and hence stationary, probability (system failure/damage risk) \(p_{k} \left( \lambda \right): = {\text{Prob}}\left\{ {R_{j} > \eta_{j}^{\lambda } {|} R_{j - 1} \le \eta_{j - 1}^{\lambda } , R_{j - k + 1} \le \eta_{j - k + 1}^{\lambda } } \right\}\) for \(j\ge k\) is independent of \(j\) and only dependent on the conditioning number \(k\). Hence, the non-exceedance probability may be approximated similarly to the conditional exceedance rate method

$$ P_{k} \left( \lambda \right) \approx {\text{exp }}\left( { - N \cdot p_{k} \left( \lambda \right)} \right),\quad k \ge 1. $$
(8)

Note that Eq. (8) follows from Eq. (3) if neglecting \(\text{Prob}({R}_{1}\le {\eta }_{1}^{\lambda })\approx 1\), as design failure/damage probability being of a small order of magnitude, with \(N\gg k\). Note that Eq. (8) is similar to a well-known mean up-crossing rate equation for the hazard/failure probability/risk (probability of exceedance) (Gaidai & **ng, 2022a, b; Madsen et al., 1986; Rice, 1944). There is convergence with respect to the conditioning parameter \(k\)

$$ P = \mathop {\lim }\limits_{k \to \infty } P_{k} \left( 1 \right);\quad p\left( \lambda \right) = \mathop {\lim }\limits_{k \to \infty } p_{k} \left( \lambda \right) $$
(9)

Note that Eq. (9) for \(k=1\) turns into a well-known non-exceedance (survival) probability relationship with a corresponding mean up-crossing rate function

$$ P\left( \lambda \right){ } \approx {\text{exp }}( - \nu^{ + } \left( \lambda \right)\,T); \quad \nu^{ + } \left( \lambda \right) = \mathop \int \limits_{0}^{\infty } \zeta p_{{R\dot{R}}} \left( {\lambda ,\zeta } \right)d\zeta $$
(10)

with \({\nu }^{+}(\lambda )\) denoting mean-up-crossing rate of the risk level \(\lambda \) for the above assembled non-dimensional vector \(R\left(t\right)\), assembled from scaled MDOF EH system components \(\left(\frac{X}{{\eta }_{X}}, \frac{Y}{{\eta }_{Y}}, \frac{Z}{{\eta }_{Z}}, \dots \right)\). The mean-up-crossing rate is given by Rice's formula, given in Eq. (10) with \({p}_{R\dot{R}}\) being joint PDF for \(\left(R, \dot{R}\right)\) with \(\dot{R}\) being time derivative \(R{\prime}\left(t\right)\) (Rice, 1944). Equation (10) relies on the so-called Poisson assumption, implying that upcrossing events of critical/high \(\lambda \) levels (in this study \(\lambda \ge 1\)) may be assumed to be nearly independent. For narrow band EH systems, displaying cascading/clustering hazards/failures in various system components, temporally successive components local maxima (caused by inherent inter-dependency between EH system extreme events) manifest themselves through highly correlated local maxima clusters, stored within assembled EH system vector \(\overrightarrow{R}=\left({R}_{1}, {R}_{2}, \dots ,{R}_{N}\right)\). The stationarity assumption was applied in the examples above, but the suggested method may also be used to handle nonstationary cases. Given the in situ scatter diagram having \(m=1,..,M\) environmental states, each individual short-term environmental state has individual probability \({q}_{m}\), so that \(\sum_{m=1}^{M}{q}_{m}=1\). Let one introduce a long-term statistical equation

$$ p_{k} \left( \lambda \right) \equiv \mathop \sum \limits_{m = 1}^{M} p_{k} \left( {\lambda ,m} \right)q_{m} $$
(11)

with \({p}_{k}(\lambda ,m)\) being same function, as in Eq. (7), corresponding to a specific short-term environmental state, with number \(m\). Note that within recent years authors have successfully verified the recommended approach’s correctness for a wide range of 1-dimensional dynamic systems (Gaidai & **ng, 2022b). Next, following the extrapolation Naess–Gaidai (NG) technique is introduced, being asymptotically of Gumbel distribution type, and serving as the foundation for failure/hazard PDF-tail extrapolation. The latter strategy is predicated on the notion that a class of parametric functions required for extrapolation in general case may be described in a manner akin to that of the relationship between Gumbel distribution and Generalized Extreme Value (GEV) distribution family. Extreme values that may be detected from sampled time series do not always follow asymptotic distributions, or to say the least, it is often quite challenging to establish that they are indeed asymptotic. The latter suggests that it is important to extend focus to a range of sub-asymptotic levels. Hence, it is suggested that the NG class of sub-asymptotic distributions be appended to the asymptotic Gumbel functional class. The above introduced \({p}_{k}(\lambda )\) as functions being regular in PDF tail, specifically for values of parameter \(\lambda \) approaching, and exceeding \(1\). For \(\lambda \ge {\lambda }_{0}\), PDF tail behaves similarly to \({\text{exp}}\left\{-{\left(a\lambda +b\right)}^{c}+d\right\}\) with four parameters \(a, b, c, d\) being suitably fitted 4 constants, for suitable PDF tail cut-on \({\lambda }_{0}\) value

$$ p_{k} \left( \lambda \right) \approx {\text{exp}}\left\{ { - \left( {a_{k} \lambda + b_{k} } \right)^{{c_{k} }} + d_{k} } \right\}, \quad \lambda \ge \lambda_{0} $$
(12)

By plotting \({\text{ln}}\left\{{\text{ln}}\left({p}_{k}(\lambda )\right)-{d}_{k}\right\}\) versus \({\text{ln}}\left({a}_{k}\lambda +{b}_{k}\right)\), often nearly linear PDF tail behavior being observed. It is useful to do the optimization on the logarithmic level by minimizing the following error function F with respect to 4 parameters \({a}_{k}, {b}_{k}, {c}_{k},{d}_{k}\)

$$ F\left( {a_{k} , b_{k} , c_{k} ,d_{k} } \right) = = \mathop \int \limits_{{\lambda_{0} }}^{{\lambda_{1} }} \omega \left( \lambda \right)\left\{ {{\text{ln}}\left( {p_{k} \left( \lambda \right)} \right) - d_{k} + \left( {a_{k} \lambda + b_{k} } \right)^{{c_{k} }} } \right\}^{2} {\text{d}}\lambda , \quad \lambda \ge \lambda_{0} $$
(13)

with \({\lambda }_{1}\) being suitable PDF tail cutoff value, namely the largest \(\lambda \)-parameter value, where the confidence interval width is still acceptable. Optimal values of four parameters \({a}_{k}, {b}_{k}, {c}_{k},{d}_{k}\) may also be determined using the sequential quadratic programming (SQP) method incorporated in the NAG Numerical Library (Numerical Algorithms Group, 2010). Weight function \(\omega \) can be defined as \(\omega \left(\lambda \right)={\left\{{\text{ln}}{\text{CI}}^{+}\left(\lambda \right)-{\text{ln}}{\text{CI}}^{-}\left(\lambda \right)\right\}}^{-2}\) with \(\left({\text{CI}}^{-}\left(\lambda \right),{ \text{CI}}^{+}\left(\lambda \right)\right)\) being 95% confidence interval (CI), empirically estimated from simulated/measured underlying dataset (Gaidai & **ng, 2022a, b; Gaidai et al., 2022b, c, d, e). For levels of \(\lambda \) approaching \(1\), the approximate limits of a p-% confidence interval (CI) of \({p}_{k}\left(\lambda \right)\) can be given as follows

$$ {\text{CI}}^{ \pm } \left( \lambda \right) = p_{k} \left( \lambda \right)\left( {1 \pm \frac{f\left( p \right)}{{\sqrt {\left( {N - k + 1} \right)p_{k} \left( \lambda \right)} }}} \right)\,. $$
(14)

with \(f(p)\) being estimated from an inverse normal distribution, for example \(f\left(90\%\right)=1.65\), \(f\left(95\%\right)=1.96\) with \(N\) being total number of EH system component’s local maxima, constituting system vector \(\overrightarrow{R}\).

The purpose of this discussion now is to address extrapolation in light of the data quality that underlies it, namely the raw PDF, CDF, and mean upcrossing rate functions tails (\(\lambda >{\lambda }_{\text{cut on}}\)) inherent anomalies. Since the mean upcrossing rate function tail has been created, by integrating the PDF tail, it is now evident that the PDF tail will be less continuous than the CDF and mean upcrossing rate function tails. In order to combat raw tail discontinuities, as seen in Fig. 2a), the authors first propose integrating mean upcrossing rate functions tail in this study.

Fig. 2
figure 2

a Integration to combat raw tail roughness. b “Fat tail” transformation, star marks \(\lambda \)-value where NG extrapolation began. Negative decimal log probability scale on the y-axis

Full size image

As a transition from a convex to a concave tail shape, we secondly propose a logarithmic transformation of the integrated mean upcrossing rate functions tail to the so-called “fat tail” condition. More specifically, \(\int {\nu }^{+}\left(\lambda \right)\to \text{ln}\left(1+\int {\nu }^{+}\left(\lambda \right)\right)\) transformation has been suggested, Fig. 2b).

The recommended approach and the NG extrapolation (modified four-parameter Weibull) method are compared in Fig. 3, with a star designating the start of extrapolation. By retaining only each 100th point from the original dataset, a shorter dataset was created by 100-fold thinning the original dataset. By comparing anticipated outcomes based on the shorter dataset with findings based on the entire dataset, the recommended technique was validated in this manner. The modified Weibull extrapolation predicted a convex tail rather than a concave one, as seen in Fig. 3, but the recommended technique was performed quite accurately.

Fig. 3
figure 3

Comparison of the suggested method versus NG (modified Weibull) extrapolation. Negative decimal log probability scale on the y-axis

Full size image

Results

When the wind speeds reach greater levels, EH efficiency will significantly fall, hence piezoelectric energy harvesters always try to scavenge energy from low-wind speeds. As a result, a stopper may be built onto the prototype, to prevent damage in high wind conditions since the stopper will dampen the considerable vibration amplitude, brought on by relatively high wind speeds. Keep in mind that the optimal wind speed range for EH operations is below 7 m/s. Using measured voltage time-series, the total horizontal aerodynamic force acting on the EH bluff body time series has been calculated, using the following equation

$$ F = \frac{{C_{p} }}{\theta }\left( {M\ddot{V} + C\dot{V} + KV} \right) + \theta V $$
(15)

containing following experimental setup parameters: \({C}_{p}=30.5{\times 10}^{-9}\) F; \(M=4.2{\times 10}^{-3}\;\text{ kg}\); \(C=5.3{\times 10}^{-3}\;\text{ N}/(\text{m}/\text{s})\); \(K=9.7\;\text{ N}/\text{s}\); \(\theta ={5.0\times 10}^{-3}\; \text{N}/\text{V}\), Table 1. In this section, bivariate random process \(Z(t)=(X(t),Y(t))\) has been studied, consisting of voltage and corresponding total force processes \(X(t),Y(t)\), with 1st component (voltage \(X=V\)) being measured and 2nd component (force \(Y=F\)) being computed synchronously, over a certain representative time lapse \((0,T)\). Let one assume that samples \(({X}_{1},{Y}_{1}),\dots ,({X}_{N},{Y}_{N})\) have been taken at N equidistant discrete temporal instants \({t}_{1},\dots ,{t}_{N}\) within the measurement time lapse \(\left(0,T\right).\) This study utilizes bivariate joint cumulative distribution function (CDF) \(P\left(\xi ,\eta \right):=\text{ Prob }\left({\widehat{X}}_{N}\le \xi ,{\widehat{Y}}_{N}\le \eta \right)\) of the 2D vector \(\left({\widehat{X}}_{N},{\widehat{Y}}_{N}\right)\), with components \({\widehat{X}}_{N}=\text{max}\left\{{X}_{j} ;j=1,\dots ,N\right\}\), and \({\widehat{Y}}_{N}=\text{max}\left\{{Y}_{j} ;j=1,\dots ,N\right\}\). In this paper \(\xi \) and \(\eta \) being recorded voltage and corresponding total force values respectively at the same in-situ location with the same EH device, measured synchronously.

Wind speeds PDF frequently follows Weibull distribution. To describe how gallo** energy harvesters react to in situ wind speed data (Choi et al., 2007; Gaidai & ** energy harvesting in heat exchange systems under the influence of ash deposition. Energy. https://doi.org/10.1016/j.energy.2022.124175 " href="/article/10.1186/s40807-023-00085-w#ref-CR78" id="ref-link-section-d93390562e9572">2022; Zhou et al., 2019), Weibull distribution is frequently used. For EH, Fig. 4a) presents the correlation between measured voltage, and the associated total horizontal EH force. Figure 4 and Eq. (1) show that due to a small order of magnitude of \(\frac{{C}_{p}}{\theta }\), horizontal force exhibits the significant linear correlation with its underlying voltage. However, nonlinear connection predominated in the tail of the bivariate extreme distribution, Fig. 4a), and Eq. (13) due to higher values of \(\dot{V}\), \(\ddot{V}\). It has been evident that the latter occurrence needs to be accounted for in non-linear statistical analysis of PDF tails. Experimentally measured voltage and corresponding horizontal force were set as 2 relevant EH system components (dimensions) \(X, Y\) thus constituting an example of two-dimensional (2D) dynamic system. Measured maxima for each system component have been used as one-dimensional extreme threshold values \({\eta }_{X}\), \({\eta }_{Y}\). In order to unify both measured time series \(X, Y\) (EH voltage and horizontal force in this case) following scaling was performed

$$ X \to \frac{X}{{\eta_{X} }}, Y \to \frac{Y}{{\eta_{Y} }} $$
(16)

with both system components becoming now non-dimensional, and having the same hazard/failure limit equal to 1. While maintaining temporal non-decreasing order, all EH system components’ local maxima from 2 observed time series have been combined into 1 new (synthetic) time series: \(\overrightarrow{R}=\left(\text{max}\left\{{X}_{1},{Y}_{1}\right\},\dots ,\text{max}\left\{{X}_{N},{Y}_{N}\right\}\right)\) with each local maxima set \(\text{max}\left\{{X}_{j},{Y}_{j}\right\}\) being ordered within non-decreasing times, at which these local maxima of dynamic EH system occurred. An example of a non-dimensional constructed vector \(\overrightarrow{R}\) is shown in Fig. 4b), comprised EH system components local maxima for voltage and corresponding horizontal force, that are being selected as EH system two components. Extrapolation of hazard/failure PDF tail towards 1-year return period has been done. Vector \(\overrightarrow{R}\) is composed of entirely distinct system components, with different physical dimensions, it should be noted that this vector itself has no particular physical significance (Gaidai & **ng, 2023; Gaidai et al., 2023c, d, e, f, g, h; Gaspar et al., 2012; Naess et al., 2009; Xu et al., 2018). Index \(j\) is the running index of system components local maxima that were recorded in a non-decreasing temporal sequence (Gaidai et al., 2023i, j, k, l; Liu et al., 2023; Sun et al., 2023; Yakimov et al., 2023).

Fig. 4
figure 4

a measured GPEH voltage, versus corresponding total horizontal force. b scaled non-dimensional assembled system vector \(\overrightarrow{R}\)

Full size image

Extrapolation from Eq. (9) is shown in Fig. 5 in the direction of a hazard/failure state with a 1-year return period, given interest return period, and considerably beyond, \(\lambda =0.3\) cut-on value has been used. According to Eq. (12), dotted lines represent extrapolated 95% CIs. According to Eq. (8) \(p\left(\lambda \right)\) is directly related to the target hazard/failure probability \(1-P\) from Eq. (3). Hence, in agreement with Eq. (8) system hazard/failure probability \(1-P\approx {1-P}_{k}\left(1\right)\) may be assessed. Note that in Eq. (7) \(N\) corresponds to the total number of local maxima within the unified EH system vector \(\overrightarrow{R}\). Conditioning parameter \(k=2\) was found to be sufficient due to the occurrence of convergence with respect to \(k\), see Eq. (8). Advocated methodology can treat energy system’s multidimensionality, performing accurate extrapolation based only on a limited underlying dataset, utilizing measured datasets quite effectively (Gaidai et al., 2023g, 2023h, 2023i, 2023j, 2023k; Gaspar et al., 2012; Liu et al., 2023; Naess et al., 2009; Sun et al., 2023; Xu et al., 2018; Gaidai et al., 2022a).

Fig. 5
figure 5

Extrapolation of \({p}_{k}\left(\lambda \right)\) towards critical levels, corresponding to 1-year return period (indicated by star), and beyond. Extrapolated 95% Confidence Interval (CI), indicated by dotted lines

Full size image

Conclusions

Traditional reliability methods dealing with system-recorded time series do not always have the advantage of efficiently handling highly dimensional systems with nonlinear cross-correlations between different system components. The main advantage of the advocated technique is its ability to examine the reliability of high dimensional non-linear dynamic systems.

This study analyzed energy harvester's dynamic system behavior, under in situ environmental settings. The novel system reliability technique has been used to assess the likelihood of device damage, given the return period of interest. The theoretical rationale of the proposed approach has been discussed in detail. The complexity and high dimensionality of dynamic systems make it necessary to develop novel, accurate, yet robust techniques that can handle available underlying datasets, making the best use of it. Despite the fact that using direct measurement or Monte Carlo simulation to analyze the reliability of dynamic systems is appealing, it is not always affordable. This study’s methodology has already been shown successful, when used with a number of simulation models, but only for 1-dimensional system responses. Overall, quite accurate forecasts have been made. The main goal of this work was to develop a general-purpose, trustworthy, yet user-friendly multi-dimensional reliability methodology.

As seen, the suggested method produced a fairly narrow confidence interval. The suggested method might therefore be helpful for a variety of nonlinear dynamic systems reliability studies. This study demonstrates how the advocated methodology may assist designers in the accurate assessment of system damage or failure risks. To summarize pros and cons of the advocated methodology:

  • Benefits of the proposed structural reliability technique compared with traditional methods lie within the ability of novel methods to tackle high-dimensional energy harvesting systems.

  • Limitations of the advocated methodology lie within the assumption of the system’s stationarity. In case when underlying trend is present, it should be identified first.