Introduction

The water retention curve, also known as the soil water characteristic curve, reflects the saturation-dependent water-retaining capacity under a given matric suction and can be described by the phenomenological equations, such as van Genuchten [33], Brooks and Corey [4], Fredlund and **ng [8], or Kosugi [15] models. The water retention characteristics is considered to be one of the most essential properties of soils, since capillarity in wet granular soils induces material cohesion which in turn affects the soil strength [1, 6, 7, 12, 26, 29, 32, 37]. As illustrated in Fig. 1, the water retention state of an unsaturated soil can be divided into three distinct regimes depending upon the amount of liquid within the pore space: (1) the capillary regime at a high saturation level in which the pore space remains effectively saturated, (2) the funicular regime at intermediate saturation where the pore water remains continuous, and (3) the pendular regime at low degrees of saturation where remaining water phase exists in the form of droplets [5, 19, 34]. In particular, at the pendular regime, the intermolecular forces exerted on the solid-fluid interface may be strong enough such that the liquid may stick and form a pendular bridge between solid particles instead of flowing through the pore space. Although a network of liquid bridges can collectively be taken into account to infer a capillary stress tensor, similar to the effective stress (\(\varvec{\sigma }'\)) developed from the interparticle contacts, its effects at macro-scales are traditionally considered to be isotropic and incorporated into hydro-mechanically coupled models (e.g., [3, 21, 25, 31]) via an extension of effective stress principle [2]:

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma }' - p_a \varvec{I} + \chi s \varvec{I} \, \, ; \, \, s = p_a - p_w, \end{aligned}$$
(1)

where \(\varvec{\sigma }\) is the total Cauchy stress, s is the suction, \(p_a\) and \(p_w\) are the pore air and pore water pressures, respectively, and \(\chi\) is called the Bishop’s coefficient.

Fig. 1
figure 1

Three distinct regimes of a typical soil water retention curve (modified after [18])

Full size image

However, recent works have demonstrated that the orientation of force chain formed by liquid menisci at low saturation level is not necessarily isotropic since the spatial distribution of intergranular contacts tends to evolve when the soil experiences external loads while the pendular bridges may form or rupture inside the deforming granular material. For instance, by performing X-ray computed tomography imaging, Manahiloh and Muhanthan [20] investigated the spatial distribution of the liquid menisci in unsaturated soil specimens, and Higo et al. [13] observed that the rupture of liquid bridges is associated with the localized shear deformation. Soulie et al. [28] and Scholtès et al. [24] conducted a series of numerical experiments to investigate the anisotropy and path dependence of the capillary stress while Wang and Sun [36] studied the potential usage of tensorial Bishop’s coefficient, indicating that the macroscopic capillary stress tensor can also be recovered from homogenizing the intergranular bridges and branch vectors. Nevertheless, the interplay between microscopic contact force chain and pendular bridge network, and their influence on the homogenized stress measures and fabric anisotropies have not been fully investigated.

In this study, we perform a series of discrete element model (DEM) simulations to better understand the evolution of anisotropic capillarity in unsaturated soils at the pendular regime. The micromechanics of wetted granular assemblies is captured by Coulomb’s friction law with a linear contact model, coupled with a liquid bridge model developed by [23, 24] where the Young-Laplace equation is adopted to compute the capillary force. To study the interaction between intergranular contacts and pendular menisci and to quantify how the formation and ruptures of liquid bridges affect the macroscopic responses, microstructural attributes such as branch vectors, interaction forces, and their chain connectivities are homogenized into stress measures and fabric tensors. The evolution of stress and fabric anisotropies with loading-unloading-realoading cycles are also illustrated and discussed in detail.

As for notations and symbols, bold-faced and blackboard bold-faced letters denote tensors (including vectors which are rank-one tensors); the symbol ’\(\cdot\)’ denotes a single contraction of adjacent indices of two tensors (e.g., \(\textbf{a} \cdot \textbf{b} = a_{i}b_{i}\) or \(\varvec{c} \cdot \varvec{d} = c_{ij}d_{jk}\)); the symbol ‘:’ denotes a double contraction of adjacent indices of tensor of rank two or higher (e.g., \(\mathbb {C} : \mathbf {\varepsilon }\) = \(C_{ijkl} \varepsilon _{kl}\)); the symbol ‘\(\otimes\)’ denotes a juxtaposition of two vectors (e.g., \(\textbf{a} \otimes \textbf{b} = a_{i}b_{j}\)) or two symmetric second-order tensors [e.g., \((\varvec{\alpha } \otimes \varvec{\beta })_{ijkl} = \alpha _{ij}\beta _{kl}\)]. We also define identity tensors: \(\varvec{I} = \delta _{ij}\) and \(\mathbb {I} = (\delta _{ik}\delta _{jl} + \delta _{il}\delta _{jk})/2\), where \(\delta _{ij}\) is the Kronecker delta. As for sign conventions, unless specified, tensile stress and dilative pressure are considered positive.

Materials and methods

Granular domain

In this study, stress-induced anisotropy in unsaturated material within the pendular regime is investigated with a DEM assembly that replicates a poorly graded find sand. Specifically, we adopt an open-source discrete element code |YADE| [27] to generate a synthetic sphere packing and to conduct grain-scale simulations by leveraging its built-in solvers. We first define a rigid box with its six frictionless faces serving as the periodic boundaries and generate particles having radii of \(0.05 \pm 0.025\) mm with a uniform distribution therein. We then assign a fictitious low value of interparticle friction angle to each particle and slowly apply isotropic compaction by reducing the dimension of the box in an equal ratio until we obtain a stable dense packing with an isotropic fabric. Once the DEM packing reaches a static equilibrium, we terminate the process and re-assign the material properties for future simulations. Here, we adopt the same microscopic material properties used in the previous study [36] which are summarized in Table 1.

Table 1 Input material parameters for the discrete element simulations
Full size table

Figure 2(a) shows the generated assembly of spheres used in this study. The resultant discrete element packing is composed of 4,053 particles and has a periodic microstructure such that it can be considered as a representative volume element (RVE) [11, 35]. For completeness, the grain size distribution of the RVE [Fig. 2(b)] is further obtained through a numerical sieve test, which denotes that the packing has a mean diameter of \(D_{50} = 0.125\) mm and the uniformity coefficient of \(C_u = 1.5\), such that it is classified as SP by the unified soil classification system (USCS). Notice that the particle shape or other index properties may also affect the mechanical responses of the granular domain (e.g., [16, 17, 30]), however, since replicating such features requires the detailed geometrical and topological information which is not readily available, this extension will be considered in the future.

Fig. 2
figure 2

DEM sample description: a initial assembly of sphere particles and b its grain size distribution curve fitted by [9]

Full size image

Discrete element modeling

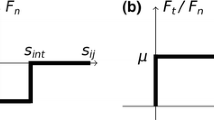
This section briefly outlines the discrete element model used in this study. In this work, we adopt the discrete element contact-friction model to simulate grain-to-grain interactions, while the liquid bridge effects are taken into account by utilizing the capillary model that solves the Young-Laplace equation (Fig. 3). From the given material properties of solid particles, the DEM contact-friction model generates the contact force between two solid particles with radii \(R_1\) and \(R_2\) when they overlap each other. In this case, the contact force can be decomposed into the normal and tangential parts, i.e., \(\textbf{f}_s = \textbf{f}_s^n +\textbf{f}_s^t\), and can be expressed as follows:

$$\begin{aligned} \textbf{f}_s^n = 2 E_s \frac{R_1 R_2}{R_1 + R_2} \textbf{u}_s^n \, \, ; \, \, \textbf{f}_s^t = {\left\{ \begin{array}{ll} - 2 \nu _s E_s \frac{R_1 R_2}{R_1 + R_2} \textbf{u}_s^t, &{} \text {if } \Vert \textbf{f}_s^t \Vert \le \Vert \textbf{f}_s^n \Vert \tan \phi _s, \\ - \Vert \textbf{f}_s^n \Vert \tan \phi _s \frac{\textbf{u}_s^t}{\Vert \textbf{u}_s^t \Vert }, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(2)

where \(\textbf{u}_s^n\) and \(\textbf{u}_s^t\) are normal overlap distance and tangential relative displacement, respectively, as illustrated in Fig. 3(a). As shown in Eq. (2), notice that interparticle friction angle imposes a threshold value which limits the maximum value of tangential force based on Coulomb’s friction law.

Fig. 3
figure 3

Illustration of exemplary a interparticle contact and b liquid bridge between two DEM particles

Full size image

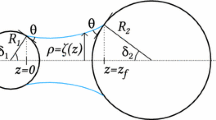
Meanwhile, the capillary model first identifies the principal radii of curvature (\(r_1\) and \(r_2\)) related to the suction s through the Young-Laplace equation [10, 29]:

$$\begin{aligned} s = \gamma \left( \frac{1}{r_1} + \frac{1}{r_2} \right) , \end{aligned}$$
(3)

where we assume a fully wetting condition (e.g., zero contact angle) for simplicity. Based on the Cartesian frame illustrated in Fig. 3(b), where the local \(\hat{x}\)-axis coincides with the axis of symmetry, two principal radii of the curvature can be computed as:

$$\begin{aligned} r_1 = - \hat{y}(\hat{x}) \sqrt{1 + \left[ \hat{y}' (\hat{x}) \right] ^2} \, \, ; \, \, r_2 = \frac{1}{\hat{y}'' (\hat{x})} \left[ 1 + \left\{ \hat{y}'(\hat{x}) \right\} ^2 \right] ^{3/2} \end{aligned}$$
(4)

where \(\hat{y}(\hat{x})\) indicates the profile of the meniscus, while the superposed prime denotes derivative with respect to \(\hat{x}\). Substituting Eq. (4) into Eq. (3) yields the following nonlinear equation that needs to be solved for the meniscus profile:

$$\begin{aligned} \frac{s}{\gamma } \left[ 1 + \left\{ \hat{y}'(\hat{x}) \right\} ^2 \right] ^{3/2} + \frac{1 + \left[ \hat{y}' (\hat{x}) \right] ^2}{\hat{y}(\hat{x})} - \hat{y}''(x) = 0. \end{aligned}$$
(5)

The capillary force between two particles induced by the liquid bridge (\(\textbf{f}_w\)) can then be obtained at the profile apex \(\hat{y}_0\) based on the gorge method [14], e.g.,

$$\begin{aligned} \textbf{f}_w = \pi \hat{y}_0 \left( 2 \gamma + \hat{y}_0 s \right) \textbf{l}, \end{aligned}$$
(6)

where \(\textbf{l}\) indicates the branch vector joining the centers of the two contacting particles, while the volume of the liquid bridge \(v_w\) can be computed as:

$$\begin{aligned} v_w = \pi \int _{\hat{x}_1^c}^{\hat{x}_2^c} \hat{y}^2(\hat{x}) \, \textrm{d}\hat{x} - \frac{1}{3} \pi \left[ R_1^3 \left( 1 - \cos \zeta _1 \right) ^2 \left( 2 + \cos \zeta _1 \right) + R_2^3 \left( 1 - \cos \zeta _2 \right) ^2 \left( 2 + \cos \zeta _2 \right) \right] , \end{aligned}$$
(7)

where \(\zeta _1\) and \(\zeta _2\) are filling angles, while \(\hat{x}_1^c\) and \(\hat{x}_2^c\) are the \(\hat{x}\)-coordinates of the solid-liquid-air interface (see Fig. 3(b)).

Spatial homogenization

At the pendular regime where pore water is no longer continuous and forms a meniscus, adjacent particles experience an additional attractive force due to the liquid bridge in between. Since previous studies [23, 24, 36], showed that the water liquid bridges form an anisotropic structure, this study adopts a particular form of total stress decomposition instead of using Bishop’s effective stress principle [Eq. (1)]:

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma }^s + \varvec{\sigma }^w, \end{aligned}$$
(8)

where \(\varvec{\sigma }^s\) and \(\varvec{\sigma }^w\) denote partial stresses exerted by solid grain contacts and by interparticle capillary forces, respectively. If a grain assembly of interest can be considered as an RVE, the partial stresses can be homogenized from the grain-scale information by using Love’s formula, e.g.,

$$\begin{aligned} \varvec{\sigma }^s= \frac{1}{V_{\text {RVE}}} \displaystyle \sum ^{N_s}_{1} \left( \textbf{f}_s \otimes \textbf{l} \right) \, \, ; \, \, \varvec{\sigma }^w= \frac{1}{V_{\text {RVE}}} \displaystyle \sum ^{N_w}_{1} \left( \textbf{f}_w \otimes \textbf{l}\right) , \end{aligned}$$
(9)

where \(V_{\text {RVE}}\) denotes the volume of the RVE, and \(N_{\alpha }\) indicates the number of solid grain contacts (if \(\alpha = s\)) or the number of liquid bridges (if \(\alpha = w\)) within the RVE. Similarly, two fabric measures that quantify the average solid contact (\(\varvec{F}^s\)) and water liquid bridge (\(\varvec{F}^w\)) orientations within the unit cell can be defined as follows:

$$\begin{aligned} \varvec{F}^s = \frac{1}{N_s} \displaystyle \sum ^{N_s}_{1} \frac{\textbf{l} \otimes \textbf{l}}{\Vert \textbf{l} \Vert ^2} \, \, ; \, \, \varvec{F}^w = \frac{1}{N_w} \displaystyle \sum ^{N_w}_{1} \frac{\textbf{l} \otimes \textbf{l}}{\Vert \textbf{l} \Vert ^2}. \end{aligned}$$
(10)

Here, \(\varvec{F}^s\) is also known as the Satake fabric tensor [22].

Recall Eq. (7) that the capillary model enables us to compute the volume of a liquid bridge. Hence, the degree of saturation \(S_w\) can also be homogenized from the wetted DEM assembly at the pendular regime as follows:

$$\begin{aligned} S_w = \frac{1}{n V_{\text {RVE}}} \displaystyle \sum ^{N_w}_{1} v_w \, \, ; \, \, n = 1 - \frac{1}{V_{\text {RVE}}} \displaystyle \sum ^{N_p}_{1} \left( \frac{4}{3} \pi r_p^3 \right) , \end{aligned}$$
(11)

where \(N_p\) is the number of particles in the RVE, \(r_p\) is the radius of an individual sphere particle, and n is the porosity.

Results and discussion

Suction effects on macroscopic responses of wetted granular material

We first investigate the suction effects on the shear stress of unsaturated granular material within the pendular regime during the series of suction-controlled triaxial compression tests. After isotropically consolidating the DEM assembly to a confining pressure of \(-10\) kPa, the displacement-controlled load is applied through moving the walls perpendicular to the z-axis [see Fig. 2(a)] with a constant strain rate of \(10^{-7} \text {s}^{-1}\), while the suction is maintained constant. In specific, we conducted four different tests with different levels of suction (\(s = 2, 5, 10\), and 20 kPa) until the axial strain \(\epsilon _a\) reaches \(-15\%\), and a test on a dried RVE that serves as a reference.

Fig. 4
figure 4

Evolution of a shear stress q and b porosity n during the numerical triaxial compression tests

Full size image

Figure 4 shows the stress-strain responses of the DEM assembly and the porosity evolution during the triaxial compression tests. Here, red (\(s = 2\) kPa), green (\(s = 5\) kPa), blue (\(s = 10\) kPa), and purple (\(s = 20\) kPa) colors indicate the results obtained from the suction-controlled tests, while black curves denote those from the reference test. As illustrated in Fig. 4(a), unsaturated DEM assemblies tend to exhibit a higher level of shear stress \(q = \sqrt{3/2} \Vert \varvec{\sigma } - {{\,\textrm{tr}\,}}{(\varvec{\sigma })} \varvec{I} / 3 \Vert\) compared to the dried case where the pendular bridge does not exist, indicating that the deviatoric part of capillary stress \(\varvec{\sigma }^w\) plays a major role in the shear behavior of the granular material. Although the existence of liquid bridges between particles has indeed a significant impact on the global mechanical behavior, the marginal difference in the shear stress response and the porosity evolution (Fig. 4) indicates that the particle gradation may affect the effectiveness of the capillary stress. In other words, as pointed out in Wang and Sun [36], the suction effect can become significant when the granular material has a high fines content. It should be also noted that, as shown in Fig. 4(b), the unsaturated granular assemblies tend to be more dilative compared to the completely dried case, due to the increase in menisci volume to maintain a constant suction, which in turn results in an increase in the degree of saturation (Fig. 5), corroborated by the previous study [23]. The result highlights that the deviatoric loading can induce anisotropy in capillary stress within the pendular regime and implies that the suction effects in wetted granular materials may not be associated with an isotropic quantity [e.g., Eq. (1)] but should be considered as a tensorial quantity as illustrated in Eq. (8).

Fig. 5
figure 5

Evolution of liquid saturation \(S_w\) during the suction-controlled triaxial compression tests

Full size image

Micromechanical investigation of stress and fabric anisotropies

This section explores how the internal structure of wetted granular assembly are affected by the deviatoric load in more great detail. Specifically, we performed an additional triaxial compression test with two loading-unloading-reloading cycles with a confining pressure of \(s = -10\) kPa. Since the results in the previous section suggest that the suction effects are marginal for poorly graded granular materials, we only focus on the case where the prescribed suction value of 10 kPa is kept constant during the simulation. Similar to the previous setup, the displacement-controlled deviatoric load is applied along the z-axis with a constant strain rate of \(10^{-7} \text {s}^{-1}\). During the simulation, we unloaded the RVE for 20,000 seconds in every \(-5 \%\) of axial strain, such that it experienced two loading-unloading-reloading cycles until reaching \(\epsilon _a = -15\%\).

Fig. 6
figure 6

Evolution of a shear stress q and b porosity n during the suction-controlled triaxial compression test with loading-unloading-reloading cycles

Full size image

As illustrated in Fig. 6(a), unloading leads to a decrease in shear stress q while reloading completes a closed-hysteresis loop. In addition, since each cycle (e.g., \(\text {B} \rightarrow \text {C} \rightarrow \text {B}\) and \(\text {D} \rightarrow \text {E} \rightarrow \text {D}\)) involves a very small change in volumetric strain, e.g., less than \(0.5 \%\) [Fig. 6(b)], the deformation corresponding to the cycle can be considered elastic.

Fig. 7
figure 7

Evolution of partial stresses \(\varvec{\sigma }^s\) and \(\varvec{\sigma }^w\): a volumetric and b deviatoric parts

Full size image

To investigate the contribution of solid grain contacts (\(\alpha = s\)) and water liquid bridges (\(\alpha = w\)), the stress-strain response obtained from the simulation is further examined in more great detail. Figure 7 shows the evolution of volumetric [\(p^{\alpha } = {{\,\textrm{tr}\,}}{(\varvec{\sigma }^{\alpha })}/3\)] and deviatoric (\(q^{\alpha } = \sqrt{3/2} \Vert \varvec{\sigma }^{\alpha } - p^{\alpha } \varvec{I} \Vert\)) parts of partial stresses, normalized against their maximum values, \(p^{\alpha }_{\text {max}}\) and \(q^{\alpha }_{\text {max}}\). By revisiting Fig. 6(b) that shows a gradual increase in unit cell volume, a constant mean pressure evolution after reaching \(\sim 5\%\) of compressive axial strain implies that the RVE tends to exhibit a pronounced plastic dilatancy. It is noted that the unloading-reloading cycle has marginal effects on the capillary stress, while it only introduces the reduction and the recovery of the volumetric and deviatoric parts of the partial stress exerted by the solid grain contacts (\(\varvec{\sigma }^s\)) during the cycle. This implies that the particles may lose contact along the unloading direction whereas the liquid bridge can be stretched but may not break until it reaches a critical interparticle distance as illustrated in Fig. 7(b). This is also evidenced by the evolution of the major (\({F}^{s}_1\) and \({F}^{w}_1\)) and minor (\({F}^{s}_3\) and \({F}^{w}_3\)) principal values of solid contact and liquid bridge fabrics shown in Fig. 8. The solid contact fabric tends to manifest a stronger anisotropy compared to that of liquid bridges during the simulation, whereas \(\varvec{F}^s\) only exhibits a noticeable closed loop during the unloading-reloading cycle, similar to Fig. 7. To better understand the grain-scale interactions, further investigation is made by examining how the distributions of contact (\(\textbf{f}_s\)) and capillary (\(\textbf{f}_w\)) forces within the DEM assembly changes during the numerical experiment [i.e., from points A to F, as specified in Fig. 6(a)]. Figure 9 shows the rose diagrams of the distributions within the xz-plane (see Fig. 2), where we set the x-axis as the \(0^{\circ }\) reference such that the deviatoric loading and unloading is applied in the direction of \(90^{\circ }\). We observe that the contact and capillary forces form isotropic network structures right after isotropically consolidating the RVE (point A), while the contact forces are aligned with the loading direction and the alignment weakens during unloading (\(\text {B} \rightarrow \text {C}\) and \(\text {D} \rightarrow \text {E}\)). On the other hand, the orientations of capillary forces tend to be weakly aligned towards the loading direction compared to those of grain contacts and less affected by the unloading of the RVE which may yield the global responses observed in Figs. 7 and 8.

Fig. 8
figure 8

Evolution of fabric anisotropies: a solid grain contacts and b liquid bridges

Full size image
Fig. 9
figure 9

Distribution of contact and capillary force orientations during the suction-controlled triaxial compression test with loading-unloading-reloading cycles

Full size image

Conclusion

In this work, discrete element simulations are carried out to study the anisotropic responses of unsaturated granular materials within the pendular regime. Based on a synthetic sphere packing that resembles a poorly graded fine sand, a series of triaxial compression tests are conducted numerically by adopting a linear contact model coupled with the solutions from the Young-Laplace equation to consider the effect of capillary forces generated by the interparticle liquid bridges therein. Macroscopic responses observed from the monotonic triaxial tests show that the capillary stress is indeed anisotropic, suggesting that its effect may not be considered as a scalar quantity at the low saturation level. We observe that the higher level of imposed suction leads to a lower volume of the liquid phase while having a marginal effect on the magnitude of deviatoric stress for poorly graded soils. Further investigation is made by conducting another numerical experiment to study the evolution of the internal structure of the RVE during the loading-unloading-reloading cycles. The results show that the anisotropies of both the partial stresses exerted by solid grain contacts and capillary forces develop during the deviatoric loading and only a marginal influence on the liquid-bridge-induced responses is observed during the cycle, implying that interparticle distances may not reach a critical distance that leads to the meniscus rupture during elastic unloading, evidenced by the evolution of the contact and capillary force orientations.