Parameter uniform numerical method for a system of two coupled singularly perturbed parabolic convection-diffusion equations

Abstract

In this paper, we propose a numerical scheme for a system of two linear singularly perturbed parabolic convection-diffusion equations. The presented numerical scheme consists of a classical backward-Euler scheme on a uniform mesh for the time discretization and an upwind finite difference scheme on an arbitrary nonuniform mesh for the spatial discretization. Then, for the time semidiscretization scheme, an a priori and an a posteriori error estimations in the maximum norm are obtained. It should be pointed out that the a posteriori error bound is suitable to design an adaptive algorithm, which is used to generate an adaptive spatial grid. It is proved that the method converges uniformly in the discrete maximum norm with first-order time and spatial accuracy, respectively, for the fully discrete scheme. At last, some numerical results are given to validate the theoretical results.

1 Introduction

In this paper, we consider the following system of two linear singularly perturbed parabolic convection-diffusion equations:

$$ \textstyle\begin{cases} \mathcal{L}_{\varepsilon } \mathbf{u}\equiv \frac{\partial \mathbf{u}}{\partial t}+\mathcal{L}_{x,\varepsilon } \mathbf{u} = \mathbf{f}(x,t),&(x,t)\in \varOmega \times (0,T]\equiv (0,1)\times (0,T], \\ \mathbf{u}(x,0)=\mathbf{u}_{0}(x),&x\in \overline{\varOmega }=[0,1], \\ \mathbf{u}(0,t)=\mathbf{u}(1,t)=\mathbf{0},&t\in (0,T], \end{cases} $$

(1)

where

$${\mathcal{L}}_{x,\epsilon }\equiv \left(\begin{array}{cc}-{\epsilon }_1\frac{{\partial }^2}{\partial x^2}& \\ & -{\epsilon }_2\frac{{\partial }^2}{\partial x^2}\end{array}\right)+A\left(\begin{array}{cc}\frac{\partial }{\partial x}& \\ & \frac{\partial }{\partial x}\end{array}\right)+B$$

and

$$A=\left(\begin{array}{cc}{a}_{11}(x)& a_{12}(x)\\ a_{21}(x)& a_{22}(x)\end{array}\right),B=\left(\begin{array}{cc}{b}_{11}(x)& b_{12}(x)\\ b_{21}(x)& b_{22}(x)\end{array}\right).$$

Here, $0<\varepsilon _{1},\varepsilon _{2}\ll 1$ are two small parameters, and $\mathbf{f}(x,t)=(f_{1}(x,t),f_{2}(x,t))^{T}$. In addition, we will assume that the data satisfies

$$\begin{aligned} a_{ii}(x)\geq \alpha _{i}>0, \quad 1\leq i\leq 2, \end{aligned}$$

(2)

with some constants $\alpha _{i}$ ($i=1,2$), and there exists a constant β such that

$$\begin{aligned} b_{ij}(x)\leq 0, \quad i\neq j, \qquad \sum _{j=1}^{2} b_{ij}(x)\geq \beta >0, \quad 1 \leq i\leq 2. \end{aligned}$$

(3)

It is well known that the exact solution of problem (1) has a multi-scale character. That is to say, there are thin layer(s) where the solution changes very rapidly, while away from the layer(s) the solution varies slowly. Therefore, to obtain a reliable numerical solution for any values of the diffusion parameters $\varepsilon _{1}$ and $\varepsilon _{2}$, some special precautions, like layer-adapted meshes or adaptive meshes, are necessary to resolve these layers and achieve high accuracy no matter how small the diffusion parameters $\varepsilon _{1}$ and $\varepsilon _{2}$ are.

If $A\equiv 0$, the above problem (1) becomes a system of singularly perturbed parabolic reaction-diffusion equations. For these problems, some robust convergence numerical approaches on layer-adapted meshes are available in the literature, e.g., Shishkina and Shishkin [1, 2], Gracia et al. [3,4,5,6], Franklin et al. [7].

If $A\not \equiv 0$, the above problem (1) is said to be a system of singularly perturbed parabolic convection-diffusion equations. Furthermore, when A is a diagonal matrix, problem (1) is said to be a weakly coupled system (i.e., coupled only through their reaction terms). Otherwise, problem (1) is called to be a strongly coupled system. As far as we know, systems of convection-diffusion equations are more delicate to handle, especially for the time-dependent convection-diffusion systems. Consequently, some researchers paid attention to the layer adapted mesh methods for some weakly coupled singularly perturbed second-order ordinary differential equation systems of convection-diffusion type; see [8,9,10,11,12] and the references therein. Recently, in [13,14,15], the authors considered some special strongly coupled system of singularly perturbed convection-diffusion problems and constructed some corresponding layer-adapted mesh approaches. Very recently, Rao and Srivastava [16] constructed a parameter uniform numerical method for a weakly coupled linear system of singularly perturbed parabolic convection-diffusion equations. As far as we know, the layer-adapted mesh approach requires a priori information about the location and width of the boundary layer. Therefore, it is very necessary to provide an adaptive moving grid approach which only uses little or no a priori information to solve a coupled system of singularly perturbed convection-diffusion problems.

In order to serve this purpose, Linß[17] constructed an adaptive moving grid method to solve a strongly coupled system of singularly perturbed second-order two-point boundary problems. However, he did not give the optimal uniform convergence analysis. For this reason, Liu and Chen [18] also developed an adaptive moving grid approach for a weakly coupled singularly perturbed system. They not only constructed a simple mesh monitor function, but also proved the uniform convergence of the presented numerical method. Furthermore, Liu and Chen [19] constructed an adaptive moving grid method for a special strongly coupled system of two singularly perturbed convection-diffusion problems and obtained an a posteriori error estimation in maximum norm.

In this paper, we will use some techniques developed in [18] to devise a uniformly convergent numerical scheme for (1) under the restriction that A is a diagonal matrix, which is also first-order accurate both in time and space direction. It should be pointed out that our adaptive grid method need not require any a priori information about the location and width of the boundary layer. Moreover, the monitor function presented in this paper is similar to arc length function which is easy to design a mesh generation algorithm.

Notations: Throughout this paper we use C, sometimes subscripted, to denote a generic positive constant that is independent of all perturbation parameters $\varepsilon _{i}$, $i=1,2$, and mesh parameters N, M. It may take different values in different places.

In our estimates, we use the $L_{\infty }$ norm and the negative norm given, respectively, by

$$\begin{aligned} \bigl\Vert w(t) \bigr\Vert _{\infty }=\operatorname{ess} \sup _{t\in [0,1]} \bigl\vert w(t) \bigr\vert ,\qquad \Vert w \Vert _{*}=\min_{W:W'=w} \bigl\Vert W(t) \bigr\Vert _{\infty }. \end{aligned}$$

For vector-valued functions $\mathbf{v}= (v_{1}(t),v_{2}(t) ) ^{T}$, set $|\mathbf{v}|= (|v_{1}(t)|,|v_{2}(t)| )^{T}$ and $\|\mathbf{v}\|_{\infty }=\max \{\|v_{1}\|_{\infty },\|v_{2}\| _{\infty } \}$.

A mesh function $\varphi := \{\varphi (t_{i}) \}_{i=0}^{N}$ is a real-valued function. Define the discrete maximum norm for such functions by $\|\varphi \|_{\infty }=\max_{i=0,1,\ldots ,N}| \varphi (t_{i})|$. For vector mesh functions $\mathbf{V}:= \{(V _{1}(t_{i}),V_{2}(t_{i}))^{T} \}_{i=0}^{N}$, we define $\|\mathbf{V}\|_{\infty }=\max \{\|V_{1}\|_{\infty }, \|V_{2}\| _{\infty } \}$.

2 The time semidiscretization

In this section, we mainly construct the time semidiscretization scheme which is important for the convergence analysis of the fully discrete scheme.

2.1 The semidiscrete scheme in time

First, we divide the time domain $[0,T]$ into M equidistant meshes with uniform time step Δt such that

$$\begin{aligned} S_{t}^{M}=\{t_{n}=n\Delta t,n=0,\ldots ,M, t_{0}=0,t_{M}=T, \Delta t=T/M \}, \end{aligned}$$

where M denotes the number of mesh intervals in the time direction.

Then, by using the backward Euler formula, we can obtain the following time semidiscrete scheme:

$$ \textstyle\begin{cases} \mathbf{u}^{0}(x)=\mathbf{u}(x,0)=\mathbf{u}_{0}(x),\quad x\in \varOmega ,\\ \mathbf{u}^{n+1}(x)+\Delta t \mathcal{L}_{x,\varepsilon } \mathbf{u}^{n+1}(x)=\mathbf{u}^{n}(x)+\Delta t \mathbf{f}(x,t_{n+1}), \\ \mathbf{u}^{n+1}(0)=\mathbf{u}^{n+1}(1)=\mathbf{0}, \end{cases} $$

(4)

where $\mathbf{u}^{n}(x)=(u_{1}^{n}(x),u_{2}^{n}(x))^{T}$ is the semidiscrete numerical solution to the exact solution $\mathbf{u}(x,t)=(u _{1}(x,t),u_{2}(x,t))^{T}$ of the continuous problem (1) at time level $t_{n}=n \Delta t$.

2.2 Convergence analysis

In the following, to analyze the uniform convergence of the solution $\mathbf{u}^{n}(x)$ of (4) to the exact solution $\mathbf{u}(x,t _{n})$ of (1), the maximum principle for equations (4) is established. Then, using this principle, a stability result is derived.

Theorem 2.1

(Maximum principle)

Assume that $(I+\Delta t L_{x,\varepsilon }) \mathbf{u}^{n+1}(x)\geq \mathbf{0}$ in Ω and $\mathbf{u}^{n+1}(0) \geq \mathbf{0}$, $\mathbf{u}^{n+1}(1)\geq \mathbf{0}$, then $\mathbf{u}^{n+1}(x)\geq \mathbf{0}$ in Ω.

Proof

Let $u_{1}^{n+1}(p)=\min_{x\in [0,1]}u_{1}^{n+1}(x)$ and $u_{2}^{n+1}(q)=\min_{x\in [0,1]}u_{2}^{n+1}(x)$. Assume without loss of generality that $u_{1}^{n+1}(p)\leq u_{2}^{n+1}(q)$ if the result of this theorem is not true. In other words, $u_{1}^{n+1}(p)<0$.

On the one hand, from the hypothesis condition $(I+\Delta t L_{x, \varepsilon })\mathbf{u}^{n+1}(x)\geq \mathbf{0}$, we have

$$\begin{array}{rl}& (I+\mathrm{\Delta }t{L}_{x,\epsilon }){\mathbf{u}}^{n+1}(p)\\ & \equiv \left(\begin{array}{c}{u}_1^{n+1}(p)-{\epsilon }_1\frac{{\mathrm{d}}^2{u}_1^{n+1}(p)}{\mathrm{d}{x}^2}+a_{11}(p)\frac{\mathrm{d}{u}_1^{n+1}(p)}{\mathrm{d}x}+b_{11}(p)u_1^{n+1}(p)+b_{12}(p)u_2^{n+1}(p)\ge 0\\ u_2^{n+1}(p)-{\epsilon }_2\frac{{\mathrm{d}}^2{u}_2^{n+1}(p)}{\mathrm{d}{x}^2}+a_{22}(p)\frac{\mathrm{d}{u}_2^{n+1}(p)}{\mathrm{d}x}+b_{21}(p)u_1^{n+1}(p)+b_{22}(p)u_2^{n+1}(p)\ge 0\end{array}\right).\end{array}$$

On the other hand, note that $p\neq 0,1$ and $\frac{\mathrm{d} u_{1} ^{n+1}(p)}{\mathrm{d} x}=0$, $\frac{\mathrm{d}^{2} u_{1}^{n+1}(p)}{ \mathrm{d} x^{2}}\geq 0$, then

$$\begin{aligned} \begin{aligned}[b] &u_{1}^{n+1}(p)-\varepsilon _{1} \frac{\mathrm{d}^{2} u_{1}^{n+1}(p)}{ \mathrm{d} x^{2}}+a_{11}(p) \frac{\mathrm{d} u_{1}^{n+1}(p)}{\mathrm{d} x}+b_{11}(p)u_{1}^{n+1}(p)+b _{12}(p)u_{2}^{n+1}(p) \\ &\quad =u_{1}^{n+1}(p)-\varepsilon _{1} \frac{\mathrm{d}^{2} u_{1}^{n+1}(p)}{ \mathrm{d} x^{2}}+ \bigl(b_{11}(p)+b_{12}(p) \bigr)u_{1}^{n+1}(p)+\bigl(u_{2}^{n+1}(p)-u _{1}^{n+1}(p)\bigr)b_{12}(p) \\ &\quad < 0, \end{aligned} \end{aligned}$$

(5)

which contradicts the hypothesis of the theorem. □

It follows from the above Theorem 2.1 that we can obtain the following Lemma 2.1 (one can see the proof of Lemma 2.2 in [20]).

Lemma 2.1

If $\mathbf{u}^{n+1}(x)$ is a solution of problem (4), then we have

$$\begin{aligned} \bigl\Vert \mathbf{u}^{n+1}(x) \bigr\Vert _{\infty }\leq C \bigl\Vert (I+\Delta t L_{x,\varepsilon })\mathbf{u}^{n+1}(x) \bigr\Vert _{\infty }, \quad x\in (0,1). \end{aligned}$$

Lemma 2.2

Let u be the solution of (1). Then there exists a constant C, independent of $\varepsilon _{1}$ and $\varepsilon _{2}$, such that

$$\begin{aligned} \biggl\vert \frac{\partial ^{i}}{\partial t^{i}} u_{j}(x,t) \biggr\vert \leq C, \quad (x,t) \in \overline{\varOmega }\times [0,T], i,j=1,2. \end{aligned}$$

Proof

The proof is similar to Lemma 3 of [16]. □

Let $\widehat{\mathbf{u}}^{n+1}(x)=(\widehat{u}_{1}^{n+1}(x), \widehat{u}_{2}^{n+1}(x))^{T}$ be the solution obtained after one step of the semidiscrete scheme (4) by taking the exact solution $\mathbf{u}(x,t_{n})$ instead of $\mathbf{u}^{n}(x)$ as the starting data. Then we have

$$ \textstyle\begin{cases} \widehat{\mathbf{u}}^{n+1}(x)+\Delta t \mathcal{L}_{x,\varepsilon } \widehat{\mathbf{u}}^{n+1}(x)=\mathbf{u}(x,t_{n})+\Delta t \mathbf{f}(x,t _{n+1}),\\ \widehat{\mathbf{u}}^{n+1}(0)=\widehat{\mathbf{u}}^{n+1}(1)= \mathbf{0}. \end{cases} $$

(6)

Lemma 2.3

Let $\mathbf{e}_{n+1}=\mathbf{u}(x,t_{n+1})-\widehat{\mathbf{u}}^{n+1}(x)$ be the local error of the time semi-discrete scheme (6). Then we obtain

$$\begin{aligned} \Vert \mathbf{e}_{n+1} \Vert _{\infty }\leq C(\Delta t)^{2}. \end{aligned}$$

(7)

Proof

It follows from (6) that the function vector $\widehat{\mathbf{u}}^{n+1}(x)$ satisfies

$$\begin{aligned} (I+\Delta t \mathcal{L}_{x,\varepsilon })\widehat{\mathbf{u}}^{n+1}(x)- \Delta t \mathbf{f}(x,t_{n+1})=\mathbf{u}(x,t_{n}), \end{aligned}$$

(8)

and as the solution $\mathbf{u}(x,t)$ is smooth enough, it holds

$$\begin{aligned} \begin{aligned}[b] \mathbf{u}(x,t_{n})&= \mathbf{u}(x,t_{n+1})+ \Delta t \mathcal{L}_{x, \varepsilon } \mathbf{u}(x,t_{n+1})-\Delta t \mathbf{f}(x,t_{n+1}) \\ &\quad {} + \int _{t_{n}}^{t_{n+1}}(t_{n}-s) \frac{\partial ^{2} \mathbf{u}}{ \partial s^{2}}(x,s)\,ds \\ &= (I+\Delta t \mathcal{L}_{x,\varepsilon })\mathbf{u}(x,t_{n+1})- \Delta t \mathbf{f}(x,t_{n+1})+O\bigl(\Delta t^{2}\bigr). \end{aligned} \end{aligned}$$

(9)

Then, from (8)–(9), we obtain

$$\begin{aligned}& (I+\Delta t \mathcal{L}_{x,\varepsilon })\mathbf{e}_{n+1}=O\bigl(\Delta t^{2}\bigr), \\& \mathbf{e}_{n+1}(0)=\mathbf{e}_{n+1}(1)=\mathbf{0}. \end{aligned}$$

Therefore, the result of this lemma can be obtained by Lemmas 2.1 and 2.2. □

Finally, based on the above Theorem 2.1, Lemmas 2.1, 2.2, and 2.3, we can obtain the following convergence result.

Theorem 2.2

Under the hypotheses of Lemmas 2.2 and 2.3, we obtain

$$\begin{aligned} \sup_{n\leq T/\Delta t} \bigl\Vert \mathbf{u}(x,t_{n})- \mathbf{u}^{n}(x) \bigr\Vert _{\infty }\leq C \Delta t. \end{aligned}$$

(10)

Thus, scheme (4) is uniformly convergent of first order.

3 The spatial discretization and adaptive spatial grid algorithm

3.1 The upwind finite difference scheme

Firstly, for each time level $t_{n}=n\Delta t$, we construct an arbitrary nonuniform spatial mesh $\overline{\varOmega }_{x}^{n}$ as follows:

$$\begin{aligned} \overline{\varOmega }_{x}^{n}=\bigl\{ 0=x_{0}^{n}< x_{1}^{n}< \cdots < x_{N}^{n}=1 \bigr\} , \end{aligned}$$

where n and $h_{i}^{n}=x_{i}^{n}-x_{i-1}^{n}$ ($i=1,\ldots ,N$) denote the time level and the spatial step size, respectively. Then, for a given mesh function $v(x_{i},t_{n})=v_{i}^{n}$, we define the forward, backward, and center difference operators $D_{x}^{+}$, $D_{x}^{-}$, and $D_{x}$ as follows:

$$\begin{aligned} D_{x}^{+}v_{i}^{n}=\frac{v_{i+1}^{n}-v_{i}^{n}}{h_{i+1}^{n}}, \qquad D_{x} ^{-} v_{i}^{n}= \frac{v_{i}^{n}-v_{i-1}^{n}}{h_{i}^{n}}, \qquad D_{x}v_{i} ^{n}= \frac{D_{x}^{+}v_{i}^{n}-D_{x}^{-}v_{i}^{n}}{\hbar _{i}^{n}}, \end{aligned}$$

where $\hbar _{i}^{n}=\frac{h_{i}^{n}+h_{i+1}^{n}}{2}$.

Finally, on $\overline{\varOmega }_{x}^{n}$, the upwind finite difference spatial discretization of (4) takes the form

$$ \textstyle\begin{cases} \mathbf{U}_{i}^{n+1}+\Delta t \mathcal{L}_{x,\varepsilon }^{N} \mathbf{U}_{i}^{n+1}=\mathbf{U}_{i}^{n}+\Delta t \mathbf{f}(x_{i}^{n+1},t _{n+1}),\quad i=1,\ldots ,N-1,\\ \mathbf{U}_{0}^{n+1}=\mathbf{U}_{N} ^{n+1}=\mathbf{0}, \end{cases} $$

(11)

where

$$\begin{aligned} \mathcal{L}_{x,\varepsilon }^{N} \mathbf{U}_{i}^{n+1}=-E D_{x} \mathbf{U}_{i}^{n+1}+A_{i}^{n+1} D_{x}^{-} \mathbf{U}_{i}^{n+1}+B_{i} ^{n+1} \mathbf{U}_{i}^{n+1} \end{aligned}$$

is the discretization of the differential operator $\mathcal{L}_{x, \varepsilon }$. Here, $\mathbf{U}_{i}^{n}=(U_{1,i}^{n},U_{2,i}^{n})^{T}$ is the numerical solution of exact solution $\mathbf{u}(x_{i},t_{n})$, $E=\operatorname{diag}(\varepsilon _{1},\varepsilon _{2})$, $A_{i}^{n+1}=A(x _{i}^{n+1})$, and $B_{i}^{n+1}=B(x_{i}^{n+1})$.

Let I be a unit matrix of order two, then scheme (11) can be expanded in the form

$$ \textstyle\begin{cases} r_{i,n+1}^{-} \mathbf{U}_{i-1}^{n+1}+r_{i,n+1}^{c} \mathbf{U}_{i} ^{n+1}+r_{i,n+1}^{+} \mathbf{U}_{i+1}^{n+1}=\eta _{i}^{n}, \quad i=1, \ldots ,N-1,\\ \mathbf{U}_{0}^{n+1}=\mathbf{U}_{N}^{n+1}=\mathbf{0}, \end{cases} $$

(12)

where

$$\begin{aligned}& r_{i,n+1}^{-}=-\frac{E}{h_{i}^{n+1}\hbar _{i}^{n+1}}-\frac{a_{i}^{n+1} \Delta t}{h_{i}^{n+1}}I,\qquad r_{i,n+1}^{+}=-E\frac{ \Delta t}{h_{i+1} ^{n+1}\hbar _{i}^{n+1}}, \\& r_{i,n+1}^{c}=I+\Delta t b_{i}^{n+1}I-r_{i,n+1}^{-}-r_{i,n+1}^{+}, \qquad \eta _{i}^{n}=\widetilde{\mathbf{U}} \bigl(x_{i}^{n+1},t_{n}\bigr)+\Delta t \mathbf{f} \bigl(x_{i}^{n+1},t_{n+1}\bigr), \end{aligned}$$

$\widetilde{\mathbf{U}}(x,t_{n})=(\widetilde{U}_{1}(x,t_{n}), \widetilde{U}_{2}(x,t_{n}))^{T}$ and $\widetilde{U}_{j}(x,t_{n})$ is the linear interpolant function through points $(x_{i}^{n},U_{j,i}^{n})$, $j=1,2$, $i=0,1,\ldots ,N$.

3.2 Adaptive spatial grid algorithm

It is well known that a common approach to construct an adaptive grid is the use of a positive monitor function $M(x)$ and the mesh equidistribution principle. That is to say, a grid $\{x_{i} \} _{i=0}^{N}$ is chosen to satisfy the following equations:

$$\begin{aligned} \int _{x_{i-1}}^{x_{i}}M(s)\,ds=\frac{1}{N} \int _{0}^{1} M(s)\,ds, \quad i=1, \ldots ,N. \end{aligned}$$

(13)

In the literature, for a single singularly perturbed differential equation, a simple monitor function is the arc-length function $M(x)=\sqrt{1+ [u'(x) ]^{2}}$ or its discrete analogue [21,22,23,24,25,26], where $u(x)$ is the exact solution of the singularly perturbed problem. Recently, Liu and Chen [18] presented an adaptive grid method to solve a weakly coupled system of two singularly perturbed convection-diffusion equations, in which they developed a monitor function as follows:

$$\begin{aligned} \widetilde{M}(x)=\sqrt{1+\max_{x\in [0,1]} \bigl\{ \bigl[ \widetilde{U} _{1}'(x) \bigr]^{2}, \bigl[ \widetilde{U}_{2}'(x) \bigr]^{2} \bigr\} }, \end{aligned}$$

(14)

where $\widetilde{U}_{j}(x)$ is the piecewise linear interpolant function passing through knots $(x_{i},U_{j,i})$, $j=1,2$, $i=0,1,\ldots ,N$. Here, in this paper, similar to (14), we choose the following monitor function:

$$\begin{aligned} M(x)=\sqrt{1+\max_{x\in [0,1]} \biggl\{ \biggl[\frac{\partial u _{1}(x,t_{n})}{\partial x} \biggr]^{2}, \biggl[\frac{\partial u_{2}(x,t _{n})}{\partial x} \biggr]^{2} \biggr\} }. \end{aligned}$$

(15)

In practical computation, the above monitor function (15) may be changed into the following discrete form:

$$\begin{aligned} \widetilde{M}(x)=\sqrt{1+\max_{x\in [0,1]} \bigl\{ \bigl[ \bigl(\widetilde{U} _{1}^{n}(x) \bigr)' \bigr]^{2}, \bigl[ \bigl(\widetilde{U}_{2}^{n}(x) \bigr)' \bigr] ^{2} \bigr\} }, \end{aligned}$$

(16)

where $\widetilde{U}_{j}^{n}(x)\in C[0,1]$ ($j=1,2$) is the piecewise linear interpolant function through the knots $(x_{i}^{n},U_{j,i}^{n})$ ($i=0,1, \ldots ,N$, $n=1,\ldots ,M$).

Therefore, to obtain an adaptive equidistribution grid and the corresponding numerical solution, we construct the following iteration algorithm:

Step 1. Let $n=1$.

Step 2. For $k=0$, let $\{x_{i}^{n,(k)}=i/N,i=0,1,\ldots ,N \}$ be the initial uniform spatial mesh for $n=1$, otherwise, choose $\{x_{i}^{n-1}\}$ for the initial mesh.

Step 3. Compute the discrete solution $\{\mathbf{U}_{i} ^{n,(k)} \}$ satisfying (12) on $\{x_{i}^{n,(k)} \}$. Let $h_{i}^{n,(k)}=x_{i}^{n,(k)}-x _{i-1}^{n,(k)}$ for each i. Let

$$\begin{aligned} \begin{aligned}[b] l_{i}^{n,(k)} &=h_{i}^{n,(k)} \sqrt{1+\max \bigl[ \bigl(D_{x}^{-} U _{1,i}^{n,(k)} \bigr)^{2}, \bigl(D_{x}^{-} U_{2,i}^{n,(k)} \bigr)^{2} \bigr]} \\ &=\sqrt{ \bigl(h_{i}^{n,(k)} \bigr)^{2}+\max \bigl[ \bigl(U_{1,i}^{n,(k)}-U _{1,i-1}^{n,(k)} \bigr)^{2}, \bigl(U_{2,i}^{n,(k)}-U_{2,i-1}^{n,(k)} \bigr) ^{2} \bigr]} \end{aligned} \end{aligned}$$

be the max arc-length between the points $(x_{i-1}^{n,(k)}, U _{j,i-1}^{n,(k)} )$ and $(x_{i}^{n,(k)}, U_{j,i}^{n,(k)} )$ in the piecewise linear computed solutions $\widetilde{U}_{j}^{n,(k)}(x)$, where $j=1,2$. Then the total max arc-length of the solution curve $\widetilde{U}_{j}^{n,(k)}(x)$ is

$$\begin{aligned} L^{n,(k)}=\sum_{i=1}^{N} l_{i}^{n,(k)}=\sum_{i=1}^{N} \sqrt{ \bigl(h_{i}^{n,(k)} \bigr)^{2}+\max \bigl[ \bigl(U_{1,i}^{n,(k)}-U_{1,i-1} ^{n,(k)} \bigr)^{2}, \bigl(U_{2,i}^{n,(k)}-U_{2,i-1}^{n,(k)} \bigr) ^{2} \bigr]}. \end{aligned}$$

Step 4. Test mesh: Let $C_{0}>1$ be a given constant. If the stop** criterion

$$\begin{aligned} \frac{\max\limits_{1\leq i\leq N}l_{i}^{n,(k)}}{L^{n,(k)}}\leq \frac{C _{0}}{N} \end{aligned}$$

(17)

holds true, then go to Step 7. Otherwise, continue to Step 5.

Step 5. Generate a new mesh by equidistributing monitor function (16): Choose points $\{0=x_{0}^{n,(k+1)}< x_{1}^{n,(k+1)}< \cdots <x_{N}^{n,(k+1)}=1 \}$ such that

$$\begin{aligned} \int _{x_{i-1}^{n,(k+1)}}^{x_{i}^{n,(k+1)}}\sqrt{1+\max _{x\in [0,1]} \bigl\{ \bigl[ \bigl(\widetilde{U}_{1}^{n,k}(x) \bigr)' \bigr] ^{2}, \bigl[ \bigl(\widetilde{U}_{2}^{n,k}(x) \bigr)' \bigr]^{2} \bigr\} }\,dx=\frac{L ^{n,(k)}}{N}, \end{aligned}$$

where $i=1,\ldots ,N$.

Step 6. Let $k=k+1$ and go to Step 3.

Step 7. Choose $\{x_{i}^{n,k-1} \}$ as the final mesh $\{x_{i}^{n} \}$ and let $U_{j,i}^{n,k-1}=U_{j,i}^{n}$.

Step 8. Let $n=n+1$, return to Step 2.

Step 9. If $n=M$, go to Step 10.

Step 10. Stop. $U_{j,i}^{n}$ is the numerical solution, grid for each time level given by $\{x_{i}^{n}\}$.

4 Error analysis

4.1 Preliminary results

For the time semi-discretization scheme (6), the maximum principle implies $\|\widehat{\mathbf{u}}^{n+1}(x)\|_{\infty }\leq C$. Now, we consider the following auxiliary boundary value problem:

$$\begin{aligned}& (I+\Delta t L_{x,\varepsilon })\delta ^{n+1}(x)=-L_{x,\varepsilon } \mathbf{u}(x,t_{n})+\mathbf{f}(x,t_{n+1}), \\& \delta ^{n+1}(0)=\delta ^{n+1}(1)=\mathbf{0}, \end{aligned}$$

whose solution is given by

$$\begin{aligned} \delta ^{n+1}(x)=\frac{\widehat{\mathbf{u}}^{n+1}(x)-\mathbf{u}(x,t _{n})}{\Delta t}. \end{aligned}$$

From $\|L_{x,\varepsilon } \mathbf{u}(x,t_{n})\|_{\infty }\leq C$ and the maximum principle, we can obtain

$$\begin{aligned} \bigl\Vert \delta ^{n+1}(x) \bigr\Vert _{\infty }\leq C, \quad x\in [0,1], n=0,1,\ldots ,M-1. \end{aligned}$$

Rewriting (6) in the form

$$ \textstyle\begin{cases} L_{x,\varepsilon } \widehat{\mathbf{u}}^{n+1}(x)=-\delta ^{n+1}(x)+ \mathbf{f}(x,t_{n+1}), \\ \widehat{\mathbf{u}}^{n+1}(0)= \widehat{\mathbf{u}}^{n+1}(1)=\mathbf{0}, \end{cases} $$

(18)

and using Lemma 3.1 of [18], we obtain the following stability result.

Lemma 4.1

Let $\widehat{\mathbf{{u}}}^{n+1}(x)$ be the solution of problem (18), then we have

$$\begin{aligned} \bigl\Vert \widehat{\mathbf{{u}}}^{n+1}(x) \bigr\Vert _{\infty }\leq C \bigl\Vert L_{x,\varepsilon } \widehat{ \mathbf{{u}}}^{n+1}(x) \bigr\Vert _{*}. \end{aligned}$$

(19)

In addition, the simple upwind finite difference scheme of (18) can be written into the following matrix form:

$$\begin{aligned}& \mathcal{L}_{x,\varepsilon }^{N} \widehat{\mathbf{U}}_{i}^{n+1}=- \delta ^{n+1}\bigl(x_{i}^{n+1}\bigr)+\mathbf{f} \bigl(x_{i}^{n+1},t_{n+1}\bigr), \end{aligned}$$

(20)

$$\begin{aligned}& \widehat{\mathbf{U}}^{n+1}(0)=\mathbf{0}, \qquad \widehat{ \mathbf{U}}^{n+1}(1)= \mathbf{0}, \end{aligned}$$

(21)

where $\widehat{\mathbf{U}}_{i}^{n+1}=(\widehat{U}_{1,i}^{n+1}, \widehat{U}_{2,i}^{n+1})^{T}$ is the approximation solution of $\widehat{\mathbf{u}}^{n+1}(x_{i}^{n+1})$. Furthermore, from Lemma 4.1, we can obtain the following result.

Corollary 4.1

Let $\widehat{\mathbf{{u}}}^{n+1}(x)$ be the solution of problem (18), $\widehat{\mathbf{U}}_{i}^{n+1}$ be the solution of (20) on an arbitrary nonuniform mesh and $\widehat{\mathbf{U}}^{n+1}(x)$ be the piecewise linear interpolant function vector through knots $(x_{i}^{n+1}, \widehat{\mathbf{U}}^{n+1} _{i})$. Then we have

$$\begin{aligned} \bigl\Vert \widehat{\mathbf{{u}}}^{n+1}(x)-\widehat{ \mathbf{U}}^{n+1}(x) \bigr\Vert _{ \infty }\leq C \bigl\Vert L_{x,\varepsilon } \widehat{\mathbf{{u}}}^{n+1}(x)-L _{x,\varepsilon } \widehat{\mathbf{U}}^{n+1}(x) \bigr\Vert _{*}. \end{aligned}$$

(22)

4.2 A priori error analysis

Based on Corollary 4.1, we get the following a priori error estimation.

Lemma 4.2

For a fixed $t_{n+1}\in (0,T]$, let $\widehat{\mathbf{{u}}}^{n+1}(x)$ be the solution of problem (18) and $\widehat{\mathbf{U}} _{i}^{n+1}$ be the solution of (20) on an arbitrary nonuniform mesh. Then we have

$$\begin{aligned} \max_{1\leq i\leq N} \bigl\vert \widehat{\mathbf{{u}}}^{n+1} \bigl(x_{i} ^{n+1}\bigr)-\widehat{\mathbf{U}}_{i}^{n+1} \bigr\vert \leq C \max_{1\leq i\leq N} \int _{x_{i-1}^{n+1}}^{x_{i}^{n+1}} \Bigl(1+ \max_{1\leq j\leq 2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Bigr)\,dx. \end{aligned}$$

(23)

Proof

It follows from Theorem 5 of [17] that

$$\begin{aligned} \begin{aligned}[b] \max_{1\leq i\leq N} \bigl\vert \widehat{ \mathbf{{u}}}^{n+1}\bigl(x_{i} ^{n+1}\bigr)-\widehat{ \mathbf{U}}_{i}^{n+1} \bigr\vert &\leq C \max _{1\leq i\leq N} \int _{x_{i-1}^{n+1}}^{x_{i}^{n+1}} \Biggl(1+ \sum _{j=1}^{2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Biggr)\,dx \\ &\leq C\max_{1\leq i\leq N} \int _{x_{i-1}^{n+1}}^{x_{i}^{n+1}} \Bigl(1+\max_{1\leq j\leq 2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Bigr)\,dx, \end{aligned} \end{aligned}$$

(24)

which completes the proof of this lemma. □

Lemma 4.3

Let $\widehat{\mathbf{u}}^{n+1}(x)=(\widehat{u}_{1}^{n+1}(x), \widehat{u}_{2}^{n+1}(x))^{T}$ be the solution of problem (18). Then there exists a constant C such that, for all $x\in [0,1]$, we obtain

$$\begin{aligned}& \bigl\vert \bigl(\widehat{u}_{1}^{n+1}(x) \bigr)' \bigr\vert \leq C \biggl(1+ \varepsilon _{1}^{-1} \exp \biggl(-\frac{\alpha x}{\varepsilon _{1}} \biggr)+ \varepsilon _{2}^{-1} \exp \biggl(-\frac{\alpha x}{\varepsilon _{2}} \biggr) \biggr), \end{aligned}$$

(25)

$$\begin{aligned}& \bigl\vert \bigl(\widehat{u}_{2}^{n+1}(x) \bigr)' \bigr\vert \leq C \biggl(1+ \varepsilon _{2}^{-1} \exp \biggl(-\frac{\alpha x}{\varepsilon _{2}} \biggr) \biggr), \end{aligned}$$

(26)

where $\alpha =\min (\alpha _{1},\alpha _{2})>0$.

Proof

Using the results given in Lemmas 3–4 of [8], we can obtain the desired results. □

Based on the above Lemmas 4.2 and 4.3, we can obtain the following convergence result.

Theorem 4.1

For a fixed $t_{n+1}\in (0,T]$, let $\widehat{\mathbf{{u}}}^{n+1}(x)$ be the solution of (18), $\widehat{\mathbf{U}}_{i}^{n+1}$ be the solution of (20) on a suitable mesh. Then we have

$$\begin{aligned} \max_{1\leq i\leq N} \bigl\vert \widehat{\mathbf{{u}}}^{n+1} \bigl(x_{i} ^{n+1}\bigr)-\widehat{\mathbf{U}}_{i}^{n+1} \bigr\vert \leq C N^{-1}. \end{aligned}$$

(27)

Proof

At first, from Lemma 4.3, we have

$$\begin{aligned} \begin{aligned}[b] \int _{0}^{1} \bigl\vert \bigl( \widehat{u}_{1}^{n+1}(x) \bigr)' \bigr\vert \,dx & \leq C \int _{0}^{1} \biggl(1+\varepsilon _{1}^{-1} \exp \biggl(-\frac{ \alpha x}{\varepsilon _{1}} \biggr)+ \varepsilon _{2}^{-1} \exp \biggl(-\frac{ \alpha x}{\varepsilon _{2}} \biggr) \biggr)\,dx \\ &=C \biggl(1+\frac{1}{\alpha } \biggl(1-\exp \biggl(-\frac{\alpha }{ \varepsilon _{1}} \biggr) \biggr) +\frac{1}{\alpha } \biggl(1-\exp \biggl(-\frac{ \alpha }{\varepsilon _{2}} \biggr) \biggr) \biggr) \\ &\leq C. \end{aligned} \end{aligned}$$

(28)

Similarly, we have

$$\begin{aligned} \int _{0}^{1} \bigl\vert \bigl( \widehat{u}_{2}^{n+1}(x) \bigr)' \bigr\vert \,dx \leq C. \end{aligned}$$

(29)

Therefore, for each $\widehat{u}_{j}^{n+1}(x)$, $j=1,2$, it follows from (28)–(29) that

$$\begin{aligned} \frac{1}{N} \int _{0}^{1} \Bigl(1+\max_{1\leq j\leq 2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Bigr)\,dx\leq CN^{-1}. \end{aligned}$$

(30)

Assume that a mesh $\{x_{i}^{n+1} \}_{i=0}^{N}$ is constructed such that

$$\begin{aligned} \int _{x_{i-1}^{n+1}}^{x_{i}^{n+1}} \Bigl(1+\max_{1\leq j\leq 2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Bigr)\,dx= \frac{1}{N} \int _{0}^{1} \Bigl(1+\max_{1\leq j\leq 2} \bigl\vert \bigl(\widehat{u}_{j}^{n+1}(x) \bigr)' \bigr\vert \Bigr)\,dx \end{aligned}$$

(31)

for $i=1,\ldots ,N$.

Finally, the desired estimate (27) follows from Lemma 4.2, (30) and (31). □

Remark 1

Theorem 4.1 gives the optimal first-order convergence of the upwind finite difference scheme uniformly in the perturbation parameters $\varepsilon _{i}$ ($i=1,2$). However, it is hard to obtain the adaptive mesh $\{x_{i}^{n+1} \}_{i=0}^{N}$ by using mesh equidistribution formula (31) since this requires the prior information about the exact solution. Thus, in practical computation, we often utilize an a posteriori error estimation and the corresponding monitor function to design a mesh generation algorithm.

4.3 A posteriori error analysis

Based on the above Lemma 4.1, we can obtain an a posteriori error estimation for the numerical scheme (20) at time level $t_{n+1}=(n+1)\Delta t$.

Theorem 4.2

For a fixed $t_{n+1}\in (0,T]$, let $\widehat{\mathbf{{u}}}^{n+1}(x)$ be the solution of (18), $\widehat{\mathbf{U}}_{i}^{n+1}$ be the solution of (20) on an arbitrary nonuniform mesh and $\widehat{\mathbf{U}}^{n+1}(x)$ be the piecewise linear interpolant function vector through knots $(x_{i}^{n+1}, \widehat{\mathbf{U}}^{n+1} _{i})$. Then we have

$$\begin{aligned} \bigl\Vert \widehat{\mathbf{{u}}}^{n+1}(x)-\widehat{ \mathbf{U}}^{n+1}(x) \bigr\Vert _{ \infty }\leq C \Bigl\{ \max _{1\leq i\leq N} h_{i}^{n+1}\max_{1\leq j\leq 2} \bigl\vert D_{x}^{-} \widehat{U}_{j,i}^{n+1} \bigr\vert + \max_{1\leq i\leq N}h_{i}^{n+1} \Bigr\} . \end{aligned}$$

(32)

Proof

From the proof of Theorems 3 and 6 in [17], an easy derivation gives

$$\begin{aligned} \bigl\Vert \widehat{\mathbf{{u}}}^{n+1}(x)-\widehat{ \mathbf{U}}^{n+1}(x) \bigr\Vert _{ \infty }\leq C\max _{1\leq i\leq N}h_{i}^{n+1} \Biggl(1+\sum _{j=1}^{2} \bigl\vert D_{x}^{-} \widehat{U}_{j,i}^{n+1} \bigr\vert \Biggr). \end{aligned}$$

(33)

It is clear that

$$\begin{aligned} \sum_{j=1}^{2} \bigl\vert D_{x}^{-} \widehat{U}_{j,i}^{n+1} \bigr\vert \leq 2\max_{1\leq j\leq 2} \bigl\vert D_{x}^{-} \widehat{U}_{j,i} ^{n+1} \bigr\vert . \end{aligned}$$

(34)

From (33)–(34), we can complete the proof of this theorem. □

Furthermore, similar to Theorem 4.1 of [18], we obtain the following result.

Theorem 4.3

Let $\widehat{\mathbf{u}}^{n+1}(x)$ be the solution of problem (18) and $\widehat{\mathbf{U}}_{i}^{n+1}$ be the solution of discrete system (20). Then we have the following bounds:

$$\begin{aligned} \max_{1\leq i\leq N} \bigl\vert \widehat{\mathbf{{u}}}^{n+1}(x_{i})- \widehat{\mathbf{U}}_{i}^{n+1} \bigr\vert \leq CN^{-1},\quad n=0,1,\ldots ,M-1. \end{aligned}$$

(35)

At last, we give the ε-uniform convergence of the fully discrete scheme (11) on the adaptive mesh produced by equidistributing the monitor function (16).

Theorem 4.4

Let $\mathbf{u}(x,t)$ be the exact solution of (1), and $\{\mathbf{U}_{i}^{n}\}$ be the discrete solution of the fully discrete scheme (11) at time level $t=n\Delta t$. Assume that $N^{-q}\leq C\Delta t$ with $0< q<1$. Then the error associated to the fully discrete scheme (11) at time level $t_{n}$ satisfies

$$\begin{aligned} \max_{1\leq i\leq N}\max_{0\leq n\leq M} \bigl\vert { \mathbf{u}}\bigl(x _{i}^{n},t_{n}\bigr)- \mathbf{U}_{i}^{n} \bigr\vert \leq C\bigl(\Delta t+N^{-1+q}\bigr). \end{aligned}$$

(36)

Proof

The proof is similar to Theorem 4.7 of [27]. □

5 Numerical examples and discussion

In this section, we show the numerical results of two examples to verify the theoretical results. For comparison purposes, we use the presented full discretization scheme (11) on the piecewise-uniform Shishkin mesh, which is constructed as follows.

We define the transition parameters $\tau _{\varepsilon _{1}}$ and $\tau _{\varepsilon _{2}}$ as

$$\begin{aligned} \tau _{\varepsilon _{2}}=\min \biggl\{ \frac{1}{2},\frac{2\varepsilon _{2}}{ \alpha }\ln N \biggr\} \quad \text{and} \quad \tau _{\varepsilon _{1}}= \min \biggl\{ \frac{1}{4},\frac{\tau _{\varepsilon _{2}}}{2},\frac{2 \varepsilon _{1}}{\alpha }\ln N \biggr\} , \end{aligned}$$

(37)

where we assume that the perturbation parameters $\varepsilon _{1}$, $\varepsilon _{2}$ satisfy $0<\varepsilon _{1}\leq \varepsilon _{2}$. A piecewise-uniform Shishkin mesh is obtained by dividing the spatial domain $[0,1]$ into three intervals such as $[0,1-\tau _{2}]$, $[1-\tau _{2},1-\tau _{1}]$, and $[1-\tau _{1},1]$. Then divide $[1-\tau _{1},1]$ into $N/2$ mesh intervals, and divide each of the other two intervals into $N/4$ mesh intervals, respectively.

For all the numerical experiments below, we will fix $C_{0}=1.2$, which is defined in (17). Furthermore, we begin with $N=32$ and $\Delta t=0.05$, and we multiply N by two and divide Δt by two. As the exact solution of the following two examples are known, for each $\varepsilon _{1}$ and $\varepsilon _{2}$, the maximum pointwise error is given by

$$\begin{aligned} E_{\varepsilon _{1},\varepsilon _{2}}^{N,M}= \bigl\Vert \mathbf{u}\bigl(x_{i} ^{n},t_{n}\bigr)-\mathbf{U}_{i}^{n} \bigr\Vert _{\infty }, \end{aligned}$$

(38)

where $\mathbf{u}(x_{i}^{n},t_{n})$ and $\mathbf{U}_{i}^{n}$ respectively indicate the exact and the numerical solution at $x_{i}$ and $t_{n}=n \Delta t$. From these values, we compute the corresponding order of convergence by

$$\begin{aligned} r_{\varepsilon _{1},\varepsilon _{2}}^{N,M}=\log _{2} \biggl(\frac{E_{ \varepsilon _{1},\varepsilon _{2}}^{N,M}}{E_{\varepsilon _{1},\varepsilon _{2}}^{2N,2M}} \biggr). \end{aligned}$$

(39)

Example 5.1

Consider the following constant coefficient problem:

$$ \textstyle\begin{cases} \frac{\partial u_{1}}{\partial t}-\varepsilon _{1} \frac{\partial ^{2} u_{1}}{\partial x^{2}}+\frac{\partial u_{1}}{\partial x} +u_{1}-u_{2}= f_{1}(x,t), \\ \frac{\partial u_{2}}{\partial t}-\varepsilon _{2} \frac{ \partial ^{2} u_{2}}{\partial x^{2}}+2 \frac{\partial u_{2}}{\partial x} -u_{1}+u_{2}= f_{2}(x,t), \end{cases} $$

(40)

with the initial boundary value conditions

$$\begin{aligned}& u_{1}(x,0)=u_{2}(x,0)=0,\quad 0< x< 1, \\& u_{i}(0,t)=u_{i}(1,t)=0, \quad 0\leq t\leq 1, i=1,2. \end{aligned}$$

We choose the source functions $f_{1}(x,t)$ and $f_{2}(x,t)$ to fit with the exact solution

$$\begin{aligned}& u_{1}(x,t)=t(C_{1}+C_{2}x-\exp \bigl(-(1-x)/ \varepsilon _{1}\bigr), \\& u_{2}(x,t)=t(C_{3}+C_{4}x-\exp \bigl(-(1-x)/ \varepsilon _{2}\bigr), \end{aligned}$$

where $C_{1}=\exp (-1/\varepsilon _{1})$, $C_{2}=1-C_{1}$, $C_{3}= \exp (-1/\varepsilon _{2})$, $C_{4}=1-C_{3}$.

For different $\varepsilon _{1}$ and $\varepsilon _{2}$, the maximum pointwise errors $E_{\varepsilon _{1},\varepsilon _{2}}^{N,M}$ and the corresponding orders of convergence $r_{\varepsilon _{1},\varepsilon _{2}}^{N,M}$ for Example 5.1 are listed in Tables 1–4, respectively. It is shown from the numerical results of Tables 1–4 that the presented adaptive grid approach is uniform first-order convergence. These numerical results are also in agreement with the theoretical estimation.

Table 1 Maximum error $E_{\varepsilon _{1},\varepsilon _{2}}^{N,M}$ for Example 5.1 using the adaptive grid method with $\varepsilon _{1}=10^{-2}$

Table 2 Rate of convergence $r_{\varepsilon _{1},\varepsilon _{2}} ^{N,M}$ for Example 5.1 using the adaptive grid method with $\varepsilon _{1}=10^{-2}$

Table 3 Maximum error $E_{\varepsilon }^{N,M}$ for Example 5.1 using the adaptive grid method with $\varepsilon _{2}=10^{-2}$

Table 4 Rate of convergence $r_{\varepsilon _{1},\varepsilon _{2}} ^{N,M}$ for Example 5.1 using the adaptive grid method with $\varepsilon _{2}=10^{-2}$

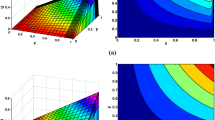
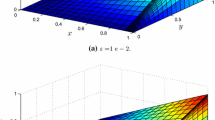
Again, to illustrate the mesh generation algorithm presented in this paper, Fig. 1 shows the final mesh obtained by the above algorithm at every time level, where Fig. 1 should be read from bottom to top. The numerical solution and exact solution of Example 5.1 for $N=M=64$, $\varepsilon _{1}=10^{-4}$, and $\varepsilon _{2}=10^{-6}$ are plotted in Figs. 2–3, respectively. These figures show the existence of the boundary layer near $x=1$. Furthermore, the maximum pointwise errors are plotted in log-log scale in Fig. 4, which reflect the fact of first-order convergence independent of $\varepsilon _{1}$ and $\varepsilon _{2}$.

Figure 1

Grid movement of the algorithm for Example 5.1 with $N=32$, $M=20$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$

Figure 2

Numerical solution of Example 5.1 for $N=M=64$, $\varepsilon _{1}=10^{-4}$, and $\varepsilon _{2}=10^{-6}$

Figure 3

Exact solution of Example 5.1 for $N=M=64$, $\varepsilon _{1}=10^{-4}$, and $\varepsilon _{2}=10^{-6}$

Figure 4

Loglog plot of the maximum error of the solution for Example 5.1 with $\varepsilon _{1}=10^{-2}$

Finally, in order to illustrate the advantage of our presented adaptive grid method, we have also compared the numerical results using adaptive grid to the numerical results of the Shishkin mesh, which is shown in Table 5 for Example 5.1. Here, to obtain the computational results of Shishkin mesh, we choose $\alpha =1$. Obviously, one can see from Table 5 that the maximum errors and the corresponding convergence orders calculated on our presented adaptive grid are lower than those calculated by using Shishkin mesh.

Table 5 Comparison of numerical results of Example 5.1 with Shishkin mesh with $\varepsilon _{2}=10^{-2}$

Example 5.2

Consider the following variable coefficient problem:

$$ \textstyle\begin{cases} \frac{\partial u_{1}}{\partial t}-\varepsilon _{1} \frac{\partial ^{2} u_{1}}{\partial x^{2}}+x\frac{\partial u_{1}}{\partial x} +2(1+x)^{2}u _{1}-(1+x^{3})u_{2}= f_{1}(x,t), \\ \frac{\partial u_{2}}{\partial t}-\varepsilon _{2} \frac{\partial ^{2} u _{2}}{\partial x^{2}}+x^{2}\frac{\partial u_{2}}{\partial x} -2xu_{1}+4 \exp (1-x)u_{2}= f_{2}(x,t), \end{cases} $$

(41)

with the initial boundary value conditions

$$\begin{aligned}& u_{1}(x,0)=C_{1}+C_{2}x-\exp \bigl(-(1-x)/ \varepsilon _{1}\bigr),\quad 0< x< 1, \\& u_{2}(x,0)=C_{3}+C_{4}x-\exp \bigl(-(1-x)/ \varepsilon _{2}\bigr),\quad 0< x< 1, \\& u_{i}(0,t)=u_{i}(1,t)=0, \quad 0\leq t\leq 1, i=1,2. \end{aligned}$$

We choose the source functions $f_{1}(x,t)$ and $f_{2}(x,t)$ to fit with the exact solution

$$\begin{aligned}& u_{1}(x,t)=\exp (-t) (C_{1}+C_{2}x-\exp \bigl(-(1-x)/\varepsilon _{1}\bigr), \\& u_{2}(x,t)=\exp (-t) (C_{3}+C_{4}x-\exp \bigl(-(1-x)/\varepsilon _{2}\bigr), \end{aligned}$$

where $C_{1}=\exp (-1/\varepsilon _{1})$, $C_{2}=1-C_{1}$, $C_{3}= \exp (-1/\varepsilon _{2})$, $C_{4}=1-C_{3}$.

For different values of $\varepsilon _{1}$ and $\varepsilon _{2}$, the maximum pointwise errors $E_{\varepsilon _{1},\varepsilon _{2}}^{N,M}$ for Example 5.2 are given in Tables 6 and 8, and the corresponding orders of convergence $r_{\varepsilon _{1},\varepsilon _{2}}^{N,M}$ are listed in Tables 7 and 9, respectively.

Table 6 Maximum error $E_{\varepsilon }^{N,M}$ for Example 5.2 using the adaptive grid method with $\varepsilon _{1}=10^{-2}$

Table 7 Rate of convergence $r_{\varepsilon _{1},\varepsilon _{2}} ^{N,M}$ for Example 5.2 using the adaptive grid method with $\varepsilon _{1}=10^{-2}$

Table 8 Maximum error $E_{\varepsilon }^{N,M}$ for Example 5.2 using the adaptive grid method with $\varepsilon _{2}=10^{-2}$

Table 9 Rate of convergence $r_{\varepsilon _{1},\varepsilon _{2}} ^{N,M}$ for Example 5.2 using the adaptive grid method with $\varepsilon _{2}=10^{-2}$

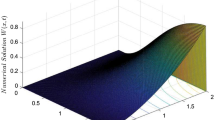
Again, to illustrate the characteristic of our adaptive grid approach, the grid movement of the algorithm for Example 5.2 with $N=32$, $M=20$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$ is shown in Fig. 5. In Figs. 6–7, the numerical solution and exact solution of Example 5.2 for $N=M=64$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$ are plotted, respectively. Moreover, the maximum pointwise errors for Example 5.2 are plotted in Fig. 8, which shows that the order of convergence of our adaptive grid method is first-order.

Figure 5

Grid movement of the algorithm for Example 5.2 with $N=32$, $M=20$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$

Figure 6

Numerical solution of Example 5.2 for $N=M=64$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$

Figure 7

Exact solution of Example 5.2 for $N=M=64$, $\varepsilon _{1}=10^{-2}$, and $\varepsilon _{2}=10^{-4}$

Figure 8

Loglog plot of the maximum error of the solution for Example 5.2 with $\varepsilon _{1}=10^{-2}$

Similarly, Table 10 also gives the maximum errors and the corresponding convergence orders obtained using the adaptive mesh approach, while we also list the results computed on Shishkin mesh, where we choose $\alpha =1$. It is shown from these results that the adaptive mesh method produces better results than those produced by using the Shishkin mesh. In summary, the adaptive grid method is quite successful for solving a system of singularly perturbed parabolic convection-diffusion equations.

Table 10 Comparison of numerical results of Example 5.2 with Shishkin mesh with $\varepsilon _{2}=10^{-2}$

6 Concluding

In this paper, we have discussed an adaptive grid method for a coupled system of two singularly perturbed parabolic convection-diffusion equations. We first apply the backward-Euler scheme to discretize problem (1) with respect to time derivative and the upwind finite difference scheme on an arbitrary nonuniform mesh to approximate the spatial derivative. Then, at each time level $t_{n}=n \Delta t$, a positive monitor function given in (16) is used to design an adaptive grid generation algorithm. An a posteriori error estimate for the proposed numerical scheme is obtained. We also establish that the presented adaptive grid approach is of first-order rate of convergence in both the spatial and temporal variables. Finally, some numerical results are conducted to support the theoretical results and also, to demonstrate the effectiveness of the adaptive spatial grid obtained by the above mesh generation algorithm.